
Differential Fault Attacks against AES Tampering with
the Instruction Flow
Silvia Mella
1
, Filippo Melzani
2
and Andrea Visconti
1
1
Universit`a degli Studi di Milano, Milano, Italy
2
STMicroelectronics, Agrate Brianza, Italy
Keywords:
Fault Attacks, AES, Differential Fault Analysis.
Abstract:
Most of the attacks against the Advanced Encryption Standard based on faults mainly aim at either altering the
temporary value of the message or key during the computation. Fewother attacks tamper the instruction flowin
order to reduce the number of round iterations to one or two. In this work, we extend this idea and present fault
attacks against the AES algorithm that exploit the misbehavior of the instruction flow during the last round.
In particular, we consider faults that cause the algorithm to skip, repeat or corrupt one of the four AES round
functions. In principle, these attacks are applicable against both software and hardware implementations, by
targeting the execution of instructions or the control logic. As conclusion countermeasures against fault attacks
must also cover the instruction flow and not only the processed data.
1 INTRODUCTION
The idea of applying faults to attack implementations
of cryptographic algorithms was presented by Boneh
et al. in 1997 (Boneh et al., 1997) against RSA
and was then extended to symmetric ciphers (Biham
and Shamir, 1997). The technique introduced against
block ciphers is referred to as Differential Fault Anal-
ysis (DFA) and consists of analyzing the difference
between correct and faulty ciphertexts in order to ob-
tain information on the secret key.
The most known DFA attacks against AES imply
fault models where the fault injection modify either a
state (Giraud, 2003; Piret and Quisquater, 2003; Tun-
stall and Mukhopadhyay, 2009; Moradi et al., 2006;
Mukhopadhyay,2009) or a round key (Chen and Yen,
2003; Kim and Quisquater, 2008) or the total amount
of round iterations (Park et al., 2011).
In this work, we present four DFA attacks that ex-
ploit faults causing a misbehavior of the process dur-
ing the final round.
In Section 2 we describe how the instruction flow
can be affected both in software and hardware imple-
mentations. In Section 3 we recall the AES algorithm
and in Section 4 we present a detailed description of
our attacks. In Section 5 we describe some methods
to obtain the desired fault models. Finally, in Section
6 we discuss how the effectiveness of some counter-
measures against faults is affected by our attacks.
2 TAMPERING WITH THE
INSTRUCTION FLOW
Most of the known DFA attacks against AES require
to corrupt a small portion of the message (or the key)
at a given cycle. Then, depending on the injection
technique, the target of the attack is either the stor-
age for the data, the bus, or the computing units while
processing the data.
But effective fault attacks can also be mounted by
tampering with the sequence of the instructions exe-
cuted by the cryptographic algorithm (Bar-El et al.,
2004). An example of tampering the instruction flow
is provided in (Schmidt and Herbst, 2008), where the
target of the attack is a software implementation of
RSA. The injected faults aim at skipping specific op-
erations within the algorithm, similarly to the attacks
we introduce in the next sections.
A practical attack of such a kind against a soft-
ware implementation of AES has been presented in
(Choukri and Tunstall, 2005). The authors were able
to skip the instruction that drives the repetition of the
rounds, effectively obtaining the AES internal state
after only one round.
These works demonstrates that attacks based on
the alteration of the sequence of instructions (even by
just skipping a single instruction) are indeed a con-
cern for software implementations of cryptographic
439
Mella S., Melzani F. and Visconti A..
Differential Fault Attacks against AES Tampering with the Instruction Flow.
DOI: 10.5220/0005112104390444
In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT-2014), pages 439-444
ISBN: 978-989-758-045-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

algorithms.
But the same reasoning can be applied to hard-
ware implementations, too. An hardware implemen-
tation of the AES algorithm can be split into three
main parts: the storage for the data, the function that
updates the data and the controller. These parts have
different logical functionalities.
The storage for the data holds the message to pro-
cess, the round keys and all the intermediate states
during the computation. Usually, the result of a round
replaces the previous state within the same memory
cells.
The function that updates the data refers to all the
combinatorial logic that is needed to compute the next
values starting from the current data. In practice, it
implements the round function and the key schedule.
The controller manages the execution, allowing to
properly drive the data through the computation. It
is composed by a mix of registers and combinatorial
logic and it is everything else that does not fall in the
two previous classes (e.g. the counter for the rounds).
An alteration of the instruction flow can be
achievedby tampering either the function that updates
data or the controller.
3 DESCRIPTION OF AES-128
The AES-128 algorithm works on 128-bit blocks by
performing a round function that involves a secret key
of 128 bits.
The 128-bit block to process can be conveniently
organized as an array of 4×4 bytes, which is the AES
state. The AES algorithm combines the plaintext P
and the key K through the bitwise XOR operation:
S
0
= P⊕ K. The round function is then applied to the
AES state 10 times.
The round function is composed by four transfor-
mations:
• SubBytes: Each byte of the state is substituted
by a new byte computed applying inversion in
GF(2
8
) and an affine transformation over GF(2);
• ShiftRows: The rows of the state are cyclically
rotated by different offsets;
• MixColumns: Each column of the state is multi-
plied in GF(2
8
) by a fixed matrix;
• AddRoundKey: The whole state is bitwise xored
with a round key of 128-bits. The round keys are
derived from the secret key, by using a KeySched-
ule procedure.
Notice that the final round of the AES algorithm
does not include the MixColumns transformation.
For details on the transformations of AES and on
the KeySchedule procedure, we remind to (National In-
stitute for Science and Technology (NIST), 2001).
4 ATTACKS
In this section, we present in theory four specific at-
tacks that target the last round of AES-128. Then, in
Section 5, we will give some examples on how to ob-
tain the desired faults.
The fault injection we consider in this section
causes the process either to skip one of the trans-
formations of the last round or to execute the Mix-
Columns transformation also during the last round.
In each attack we exploit the difference between
correct and faulty ciphertexts to obtain the value of
the temporary state just before the attacked transfor-
mation. Then, we derive the last round key K
10
, by
using the correct ciphertext, and finally we get the se-
cret key K, by inverting the KeySchedule transforma-
tion on K
10
.
Notice that, similar attacks can be conducted
against the decryption function. In this case, we will
compare correct and faulty plaintexts, directly obtain-
ing the secret key.
Before presenting the attacks, recall that, by defi-
nition, the correct ciphertext is
C = ShiftRows(SubBytes(S
9
)) ⊕ K
10
(1)
where S
9
represents the AES state at the beginning of
the last round.
4.1 SubBytes
In this attack we consider a fault that causes the exe-
cution to skip the last SubBytes operation.
Depending on the granularity of the implementa-
tion, the AES process can handle one or more bytes
per clock cycle. Therefore, the fault injection can
cause the SubBytes transformation to be not executed
either on a single byte or on the whole AES state (or
on any combination in between). Since all the bytes
are computed independently each other, the attack ap-
plies in any case.
For the sake of simplicity, we now consider that
the fault injection causes the skipping of the SubBytes
transformation for the whole state. This leads to a
faulty ciphertext
C
∗
= Shi ftRows(S
9
) ⊕ K
10
(2)
and to an observed difference between correct and
faulty ciphertexts
∆ = C⊕C
∗
= Shi ftRows(SubBytes(S
9
) ⊕ S
9
) (3)
SECRYPT2014-InternationalConferenceonSecurityandCryptography
440
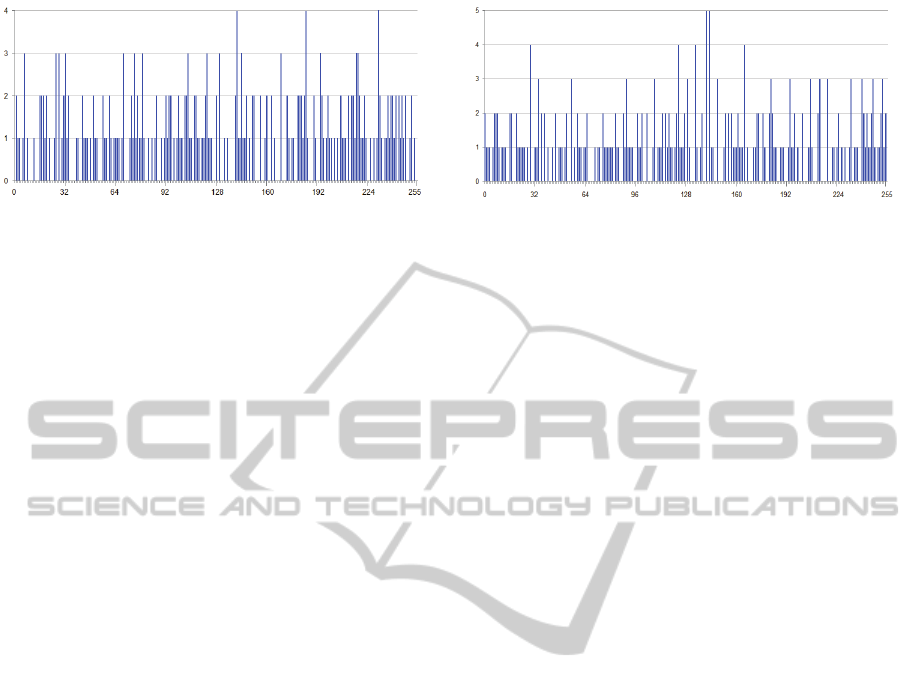
Figure 1: For any δ ∈ [0, . . . , 255], the number of bytes x
such that x⊕SubBytes(x) = δ is given.
Let us denote by i
′
the position of the i-th byte of
the state after applying the ShiftRows transformation.
Hence, for any i, we have C
i
′
= SubBytes(S
9
i
) ⊕ K
10
i
′
and C
∗
i
′
= S
9
i
⊕ K
10
i
′
.
It follows that the observed difference between
correct and faulty bytes is
∆
i
′
= C
i
′
⊕C
∗
i
′
= SubBytes(S
9
i
) ⊕ S
9
i
(4)
Before starting the analysis, it is possible to pre-
compute for any byte x ∈ [0, 255] the value:
δ = x⊕ SubBytes(x) (5)
It is then possible to fill out a table where for each
δ the bytes x that satisfy (5) are given. Figure 1
shows the number of such x for each possible δ.
We can notice that several δ’s can never occur and
that for the other δ’s the number of occurrences is
very small. In particular, in the worst case (when
δ ∈ {
0x8D
,
0xB9
,
0xE7
}) it is equal to 4.
It follows that, given ∆
i
′
only a limited number of
candidates for S
9
i
satisfy (4). Consequently, also the
set of possible candidates for K
10
i
′
= C⊕SubBytes(S
9
i
)
has been considerably reduced.
It follows that, in the worst case the search space
for K
10
has been reduced to 32 bits (2 bits for each
byte) and the attacker can obtain K with an exhaus-
tive search. Alternatively, with other pairs of correct
and faulty ciphertexts (at most three), obtained using
different plaintexts and the same key K, only the right
value of K
10
i
′
is expected to appear in the set of key
candidates of each execution.
Now, we would like to underline the fact that it
is possible to modify the fault model, provided that
it continues to leak some information on the secret.
For instance, we can consider fault models where the
SubBytes transformation is executed twice or is re-
placed by its inverse. The principles of the attack still
hold. Actually, as shown below, we can still analyze
an equation similar to 5, fill out the correspondingdis-
tribution table and observe which candidates satisfy
the obtained difference between correct and faulty ci-
phertexts.
Figure 2: For any δ ∈ [0, . . . , 255], the number of bytes x
such that InvSubBytes(x) ⊕SubBytes(x) = δ is given.
4.1.1 InvSubBytes/SubBytes
As a variant of the previous attack, we can consider
the case where a fault injection cause the inverse of
the SubBytes transformation to be executed instead
of the SubBytes itself. Such a scenario can happen
in hardware implementations that share most of the
datapath between the encryption and the decryption
functionalities. In these designs the entities for the
direct and the inverse SubBytes are both instantiated
and a multiplexer selects between the two depending
on the control bit that sets encryption or decryption.
The attack is mainly the same with the difference
that
∆
i
′
= C
i
′
⊕C
∗
i
′
= SubBytes(S
9
i
) ⊕ InvSubBytes(S
9
i
)
(6)
For any possible value of ∆
i
′
, the number of oc-
curences is given in Fig. 2. Again, with two or three
pair of correct and faulty ciphertexts, the attacker can
obtain the secret key.
4.2 ShiftRows
Now we present a possible attack when the fault
causes the skipping of the last ShiftRows operation.
Similarly to Sec. 4.1, this attack applies when the
fault injection affects whether a single row or the
whole state, since the ShiftRows operation transforms
each row independently. We consider the second case
and use the same faulty ciphertext to analyze all the
rows contemporarly.
Let us denote by s the temporary state
after the last SubBytes transformation, i.e.
s = SubBytes(S
9
). The observed differ-
ence between correct and faulty ciphertexts is
∆ = C⊕C∗ =
0 0 0 0
s
5
⊕ s
1
s
9
⊕ s
5
s
13
⊕ s
9
s
1
⊕ s
13
s
10
⊕ s
2
s
14
⊕ s
6
s
2
⊕ s
10
s
6
⊕ s
14
s
15
⊕ s
3
s
3
⊕ s
7
s
7
⊕ s
11
s
11
⊕ s
15
(7)
Notice that we cannot deduce any information
from ∆ about the first row of the state (and of the key),
because the fault injection has no effect over it. On
DifferentialFaultAttacksagainstAESTamperingwiththeInstructionFlow
441

the contrary, for the other three rows we can solve the
corresponding linear systems derived from equation
(7).
Indeed, for the second row of the state, we have
1 1 0 0
0 1 1 0
0 0 1 1
1 0 0 1
s
1
s
5
s
9
s
13
=
∆
1
∆
5
∆
9
∆
13
(8)
The matrix is singular with rank 3. Hence, the the
set of possible candidates for the 4-uple [s
1
, s
5
, s
9
, s
13
]
has dimension 2
8
.
Similarly, for the third and fourth row we obtain
2
16
and 2
8
candidates, respectively.
The search space for the state s, and consequently
for the last round key (since K
10
= s ⊕ C), has been
reduced from 128 to 64 bits (32 bits for the first row,
8 bits for the second and fourth rows and 16 bits for
the third row).
4.3 MixColumns
By definition, in the last round of AES the Mix-
Columns transformation is not executed. By inducing
a fault (for instance, by targeting the round counter),
we can make the algorithm to execute it, obtaining the
faulty ciphertext:
C
∗
= MixColumns(ShiftRows(SubBytes(S
9
))) ⊕ K
10
(9)
Let us denote by s the temporary state af-
ter the last ShiftRows transformation, i.e. s =
Shi ftRows(SubBytes(S
9
)). The observed difference
between correct and faulty ciphertexts is
∆ = C ⊕C
∗
= s⊕ MixColumns(s) (10)
By considering (10), for any column of s we have:
3 3 1 1
1 3 3 1
1 1 3 3
3 1 1 3
s
i
s
j
s
k
s
l
=
∆
i
∆
j
∆
k
∆
l
(11)
The matrix is singular with rank 3. Hence, the
set of possible candidates for each column of s has
dimension 256. It follows that the dimension of the
state space, and consequently of the key space, has
been reduced to 2
32
. With an exhaustive search, the
attacker can obtain the whole key.
Similarly to the previous attacks, we can consider
a fault injection to affect a single column of the state.
In this case, we need to conduct the attack for each
column by generating different faulty ciphertexts.
4.4 AddRoundKey
In this attack, we consider a fault that causes the exe-
cution to skip the last AddRoundKey operation.
Suppose that the fault injection affects the whole
state. This leads to a faulty ciphertext
C
∗
= Shi ftRows(SubBytes(S
9
)) (12)
The attacker can then simply add correct and faulty
ciphertexts, obtaining the last round key: C ⊕ C
∗
=
K
10
. By inverting the KeySchedule on K
10
, the secret
key K is obtained with a single pair of correct and
faulty ciphertexts.
If the fault affects only a part of the state, it is
possible to obtain the remaining bytes of the key by
generating other faulty ciphertexts.
5 FAULT INJECTION
TECHNIQUES
The attacks described in Section 4 require the abil-
ity to alter the sequence of operations executed by the
device. Such an effect can be achieved on both soft-
ware and hardware implementations. For instance, in
software implementations, it is possible to cause the
algorithm to skip an instruction. Namely, either to
skip one operation among SubBytes, ShiftRows and
AddRoundKey, or to skip the test instruction on the
round counter, in order to execute the MixColumns
also during the last round. Whereas, in hardware ar-
chitectures, it is possible to either tamper with the
controller or change the control signals that drive part
of the computational logic. For instance, the control
bit that sets encryption or decryption or the bits that
control the round counter.
Some of the methods described in literature that
allows to obtain needed effects are:
• Power spikes: The induction of power spikes can
cause the skipping of an instruction or the gather-
ing of a wrong data from a bus (K¨ommerling and
Kuhn, 1999; Bar-El et al., 2004);
• Clock Glitches: By supplying an external clock
signal, with a period significantly shorter than
the one needed by the device, the next instruc-
tion is executed before the previous one was fin-
ished (K¨ommerling and Kuhn, 1999; Bar-El et al.,
2004; Balasch et al., 2011);
• Eddy currents: An external electromagnetic field
can induces eddy currents on the surface of
the chip, which can cause a single bit fault
(Quisquater and Samyde, 2002);
SECRYPT2014-InternationalConferenceonSecurityandCryptography
442

• Laser beam: Because of the sensitivity of semi-
conductors to strong light exposure, with a fo-
cused laser beam it is possible to cause a fault
on the target chip. Even a single bit can be set
or reset (Skorobogatov and Anderson, 2002; van
Woudenberg et al., 2011).
In order to clarify the feasibility of the attacks pre-
sented in this work, we now describe how desired
faults can be injected on a software implementation
of AES on a microcontroller, using power and clock
glitches. In order to do it, we leverage on some re-
sults presented in previous works that applied these
techniques (Choukri and Tunstall, 2005; Schmidt and
Herbst, 2008; Bar-El et al., 2004). In particular, in
(Choukri and Tunstall, 2005), a software implemen-
tation of AES on a smart card is considered where the
round steps are sequentially executed and a jump con-
dition manages the round counter. With a single glitch
on the power supplied to the smart card, they are able
to skip exactly the “conditional jump”, with the effect
of reducing the number of rounds to one. Whereas,
in (Schmidt and Herbst, 2008; Bar-El et al., 2004) the
RSA and DES algorithm are attacked by skipping tar-
get instructions, always by using power glitches.
A first step for the attack consists of the character-
ization of the device by determining the configuration
that causes the proper glitch. This can be achieved by
conducting several experiments where the clock pe-
riod, the applied voltage and the duration of the glitch
are varied.
As a second phase, the portion of the code where
to inject a fault must be determined. This can be
achieved by examining the executed code in details
and by estimating the length of interesting instruc-
tions in terms of clock cycles.
A third phase consists of determining when the
target instruction is executed by the device. By mea-
suring the current consumption of the smart card, it
is possible to observe a pattern that repeats itself nine
times and a shorter final pattern due to the absence of
the MixColumns operation in the final round.
Once the right position and the size of the glitch
have been found, the power supply is interrupted or
lowered. This results in operations to be skipped.
For a detailed experiment on a specific device, we
remind to (Choukri and Tunstall, 2005), where con-
crete parameter settings and time costs are provided.
Also for hardware implementations, the described
techniques can cause desired faults. For instance, a
clock glitch in a specific clock cycle allows to skip an
instruction.
6 COUNTERMEASURES
The presented attacks can affect the effectiveness of
some countermeasures that protect AES implemen-
tations against fault attacks. In particular counter-
measures based on redundancy are concerned. For
a description of such countermeasures, we remind
to (Schmidt and Medwed, 2012; Bousselam et al.,
2012).
A class of countermeasures uses coding tech-
niques to add redundancy on the AES computation.
In most of the proposed cases such error detec-
tion/correction codes are applied to the AES state and
key only. This means for instance that when an oper-
ation is skipped the encoding of the data can be still
valid and then the countermeasure fails in detecting
the attack.
Some form of redundancy can be introduced with
the round counter, in order to protect the “conditional
jumps” and make the attack in (Choukri and Tunstall,
2005) unfeasible. However, this kind of countermea-
sure will not be successful against the attacks pre-
sented in this work, even if the attacker is using the
same resources and techniques of the attacker that re-
duces the number of rounds.
Another countermeasure is based on the duplica-
tion of all, or parts of, the algorithm. This would make
the attacks more difficult, since a double fault injec-
tion would be necessary. However, such a solution
has a significant impact on the performance of the al-
gorithm and is not recommended.
The inclusion of a random delay in the algorithm
makes the detection of target instructions more com-
plicated. This results in a more difficult achievement
of successful attacks, but it is still possible to design
the attack in order to ignore the random effects.
An additional method for protecting against fault
attacks consists of using sensors on the microcon-
trollers to detect fault injections. But, different sen-
sors should be used for different fault injection tech-
niques and this can be an excessively expensive solu-
tion for general purpose microcontrollers.
7 CONCLUSIONS
Most of the known attacks based on faults against
AES specifically target the processed data, i.e. the
message or the key. But the memory that stores the
intermediate data is not the only portion of the device
where faults can occur. Actually, a small number of
attacks in literature is based on the alteration of the
instruction flow, specifically on the reduction of the
number of rounds to one or two.
DifferentialFaultAttacksagainstAESTamperingwiththeInstructionFlow
443

By extending the idea of targeting the instruction
flow, instead of the data, we presented some new at-
tacks against AES that exploit misbehaviors of the al-
gorithm execution. In particular, we have shown how
a differential fault analysis can be conducted when the
main operations that compose the AES round func-
tion are corrupted, skipped or repeated during the fi-
nal round.
We have also provided some examples of the in-
jection techniques that may lead to desired faults,
such as power and clock glitches, and we have shown
how common countermeasures against fault attacks
behave against our new attacks.
REFERENCES
Balasch, J., Gierlichs, B., and Verbauwhede, I. (2011). An
in-depth and black-box characterization of the effects
of clock glitches on 8-bit mcus. In (Breveglieri et al.,
2011), pages 105–114.
Bar-El, H., Choukri, H., Naccache, D., Tunstall, M., and
Whelan, C. (2004). The sorcerer’s apprentice guide
to fault attacks. IACR Cryptology ePrint Archive,
2004:100.
Biham, E. and Shamir, A. (1997). Differential fault analysis
of secret key cryptosystems. In Jr., B. S. K., editor,
CRYPTO, volume 1294 of Lecture Notes in Computer
Science, pages 513–525. Springer.
Boneh, D., DeMillo, R. A., and Lipton, R. J. (1997). On
the importance of checking cryptographic protocols
for faults (extended abstract). In Fumy, W., editor,
EUROCRYPT, volume 1233 of Lecture Notes in Com-
puter Science, pages 37–51. Springer.
Bousselam, K., Natale, G. D., Flottes, M.-L., and Rouzeyre,
B. (2012). On countermeasures against fault attacks
on the advanced encryption standard. In (Joye and
Tunstall, 2012), pages 89–108.
Breveglieri, L., Guilley, S., Koren, I., Naccache, D., and
Takahashi, J., editors (2011). 2011 Workshop on Fault
Diagnosis and Tolerance in Cryptography, FDTC
2011, Tokyo, Japan, September 29, 2011. IEEE.
Chen, C.-N. and Yen, S.-M. (2003). Differential fault anal-
ysis on aes key schedule and some coutnermeasures.
In Safavi-Naini, R. and Seberry, J., editors, ACISP,
volume 2727 of Lecture Notes in Computer Science,
pages 118–129. Springer.
Choukri, H. and Tunstall, M. (2005).
Round reduction using faults.
http://www.geocities.ws/mike.tunstall/papers/CT05.
Giraud, C. (2003). Dfa on aes. IACR Cryptology ePrint
Archive, 2003:8.
Joye, M. and Tunstall, M., editors (2012). Fault Analysis
in Cryptography. Information Security and Cryptog-
raphy. Springer.
Kim, C. H. and Quisquater, J.-J. (2008). New differen-
tial fault analysis on aes key schedule: Two faults are
enough. In Grimaud, G. and Standaert, F.-X., editors,
CARDIS, volume 5189 of Lecture Notes in Computer
Science, pages 48–60. Springer.
K¨ommerling, O. and Kuhn, M. G. (1999). Design
principles for tamper-resistant smartcard processors.
https://www.cl.cam.ac.uk/ mgk25/sc99-tamper.pdf.
Moradi, A., Shalmani, M. T. M., and Salmasizadeh, M.
(2006). A generalized method of differential fault at-
tack against aes cryptosystem. In Goubin, L. and Mat-
sui, M., editors, CHES, volume 4249 of Lecture Notes
in Computer Science, pages 91–100. Springer.
Mukhopadhyay, D. (2009). An improved fault based attack
of the advanced encryption standard. In Preneel, B.,
editor, AFRICACRYPT,volume 5580 of Lecture Notes
in Computer Science, pages 421–434. Springer.
National Institute for Science and Technol-
ogy (NIST) (2001). Advanced En-
cryption Standard (FIPS PUB 197).
http://www.csrc.nist.gov/publications/fips/fips197/fips-
197.pdf.
Park, J., Moon, S., Choi, D., Kang, Y., and Ha, J. (2011).
Differential fault analysis for round-reduced aes by
fault injection. In ETRI Journal, volume 33, pages
434–442.
Piret, G. and Quisquater, J.-J. (2003). A differential fault
attack technique against spn structures, with applica-
tion to the aes and khazad. In Walter, C. D., C¸ etin
Kaya Koc¸, and Paar, C., editors, CHES, volume 2779
of Lecture Notes in Computer Science, pages 77–88.
Springer.
Quisquater, J.-J. and Samyde, D. (2002). Eddy current for
Magnetic Analysis with Active Sensor. In Esmart
2002, Nice, France.
Schmidt, J.-M. and Herbst, C. (2008). A practical fault
attack on square and multiply. In Breveglieri, L.,
Gueron, S., Koren, I., Naccache, D., and Seifert, J.-P.,
editors, FDTC, pages 53–58. IEEE Computer Society.
Schmidt, J.-M. and Medwed, M. (2012). Countermeasures
for symmetric key ciphers. In (Joye and Tunstall,
2012), pages 73–87.
Skorobogatov, S. P. and Anderson, R. J. (2002). Opti-
cal fault induction attacks. In Jr., B. S. K., C¸ etin
Kaya Koc¸, and Paar, C., editors, CHES, volume 2523
of Lecture Notes in Computer Science, pages 2–12.
Springer.
Tunstall, M. and Mukhopadhyay, D. (2009). Differential
fault analysis of the advanced encryption standard us-
ing a single fault. IACR Cryptology ePrint Archive,
2009:575.
van Woudenberg, J. G. J., Witteman, M. F., and Menarini,
F. (2011). Practical optical fault injection on secure
microcontrollers. In (Breveglieri et al., 2011), pages
91–99.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
444
