Secure Key Distribution based on Meteor Burst Communications

Amir I. Sulimov and Arkadij V. Karpov

Department of Radio Physics, Institute of Physics, Kazan Federal University,

Kremlyovskaya St., Kazan, Russia

Keywords: Encryption Keys Distribution, Common Randomness, Meteor Burst Radio Propagation, Channel

Reciprocity, Randomness of Carrier Phase, Randomness of Propagation Time, Randomizing Factor.

Abstract: The paper discusses possibility of secure encryption keys distribution based on stochastic properties of

meteor burst radio propagation. Unlike wireless key distribution, this method provides much greater channel

length and key distribution distances, which is up to 2000 km. Another important advantage is an ability of

meteor burst communications to operate in severe climate, under conditions of polar and other remote areas.

The paper also considers various physical factors ensuring stochastic variations in characteristics of received

radio signal, which are applicable for the secret key generation. The simulation results revealing the most

important randomizing factors within meteor burst channel are presented.

1 INTRODUCTION

Over the last 25-30 years there is an active

discussion in the publications of a large number of

researchers about the possibility of secure key

distribution based on stochastic properties of

physical layer of data channels. Historically, the first

method to realize this idea was the quantum key

distribution proposed in the mid-1980s (Bennett,

1984). Ten years after, the idea of encryption keys

distribution based on physical properties of

reciprocal radio channels was proposed (Hershey,

1995). In many subsequent works, such as (Mathur,

2008; Madiseh, 2008; Madiseh, 2009), the multipath

fading effect within indoor environment and its

unpredictability have been considered as a common

source of randomness to create a shared secret key at

two parties (say, Alice and Bob). The channel

reciprocity ensured symmetry of the key instances at

Alice and Bob. The secret key was generated based

on random signal characteristics (e.g. phase,

amplitude and quadrature components), whose

measurements were identical at both sides of the

link. A rapid spatial decorrelation of multipath

signal characteristics ensured inability of key

interception even at small spatial diversities.

A short-range radio is the main drawback of

multipath channel, which typically limits key

distribution distances by 1 km only. However, the

years of research and development in the field of

meteor burst communication systems have shown

that, like the multipath channels, the meteor radio

propagation has all properties necessary for the key

distribution.

The purpose of this paper is to show that the

stochastic properties of meteor radio propagation

(MRP) provide encryption keys generation and their

secure distribution over the distances up to 2000 km.

2 METEOR PHENOMENA AND

“METEOR CRYPTOGRAPHY”

Every second a countless number of meteor particles

invade into the Earth's atmosphere at the speed of 12

to 72 km/s. These particles are so small that their

weights range from 0.01 mg to several grams only.

Under the influence of a high atmospheric drag the

meteor particles burn at altitudes of 70-120 km

leaving ionized trails behind them. These trails

scatter incident radio waves acting as natural

retranslators. Thus, emitted by Alice radio signal is

reflected from a meteor trail and will be eventually

received by Bob. So, a meteor burst communication

link is established between Alice and Bob. In fact,

only a small part of all meteor trails is suitable for

the communication between the given locations of

Alice and Bob to arise. To be more specific, the

communication will come only if a trail provides

445

Sulimov A. and Karpov A..

Secure Key Distribution based on Meteor Burst Communications.

DOI: 10.5220/0005113104450450

In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT-2014), pages 445-450

ISBN: 978-989-758-045-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

desired geometry of scattering and sufficient signal

strength.

Typically, only 50-350 suitable meteor trails are

observed within 1 hour. This is a small number,

which naturally leads to a small (a few hundreds

bps) capacity of meteor burst communication

systems. However, the meteor burst channel (MBC)

has a number of particular properties that can be

used for the secure generation and distribution of

encryption keys. According to experimental studies

(Desourdis, 1993) the MBC can be considered as a

reciprocal channel with a satisfactory

approximation. Just like in the case of multipath

fading channels, it allows detection of identical

values of random signal characteristics both by Alice

and Bob.

The scattering by meteor trails can be

approximately regarded as a specular reflection from

a certain point M lying on its surface (McKinley,

1961). This leads to a limited area around the

communication point where the scattered signal can

be received. Obviously, the strongest signal will be

received at the direction of specular reflection and a

rapid spatial decorrelation will be observed with the

rise of diversity. Such decorrelation makes key

interception almost impossible at practice.

Finally, a significant randomness exists within

the MBC. The invasion of meteor particles into the

Earth's atmosphere along with its ablation and

formation of ionized trail, emergence of the

reflecting point M are mostly unpredictable

processes. Specifically, the coordinates of the

reflecting point M are also random. This causes

randomness of the A-M-B path for the signal

transmitted from Alice to Bob. As a result, random

values of the carrier phase φ, time delay τ and

amplitude U will be detected at the signal receiving.

These values should be identical at both sides of the

link due to channel reciprocity:

;φ

;τ

}={U

;φ

;τ

}. Thus, the MBC

channel can be considered as a common source of

randomness for Alice and Bob. This allows them to

create a shared secret key by performing at both

sides a series of measurements of random

characteristics of radio reflections from the meteor

trails. The authors called such an approach to

encryption keys distribution the “meteor

cryptography".

3 PREVIOUS WORKS

The concept of meteor cryptography was proposed

by researchers from Kazan Federal University

(Russia) in 2001. This idea was preceded by almost

50 years of active theoretical and experimental

studies in the field of meteor radio propagation and

system development for the meteor burst

communication and time synchronization. As a

result of this hard work, the prototypes of meteor

burst synchronization systems with sub-nanosecond

accuracy were created (Sidorov, 1993; Korneyev,

2003; Korneyev, 2007). Such accuracy allows

synchronous detection of received signal carrier

phase at both sides of the meteor burst

communication link. It was experimentally shown

(Desourdis, 1993) that the phase values measured at

both sides of the link are very close to each other.

It should be noted, that in typical meteor burst

communication link signal propagates over the

distances of hundreds kilometers. Besides, due to

randomness of coordinates of the reflecting point at

meteor trail the propagation path is also random. As

a result, the carrier phase of received signal is a

random variable which could be used for the

encryption keys generation.

In previous works (Karpov, 2005; Sidorov, 2007)

on meteor cryptography the main efforts were

focused at the discussion of technical aspects of

implementation of encryption key distribution

systems. However, we feel that a very important part

of the research work has been missed. It was not

taken into account that the meteor burst

communications is a very specific technical field

familiar only to a limited number of specialists. The

basic principles of meteor cryptography were not

disclosed properly in the prior works. In particular,

the sources of randomness within the meteor burst

channel have not been indicated.

The following sections of this paper are devoted

to discussion of basic mechanisms of the MBC

randomness. A significance of different randomizing

factors will also be investigated for the values of

carrier phase φ and propagation delay τ of meteor

radio reflections.

4 RESEARCH METHODS

Meteor burst channel is difficult in understanding.

Its performance is influenced by many factors of

different nature: by equipment, astronomical,

atmospheric conditions, etc. All these factors have a

complex impact on the measured signal parameters.

SECRYPT2014-InternationalConferenceonSecurityandCryptography

446

Unfortunately, we can’t separate them in an

experiment, which makes a study of individual

influence of each randomizing factor impossible.

Moreover, the scattering from meteor trails takes its

place at random coordinates at altitudes of 80-110

km. Thus, immediate observation and control of

propagation of radio signals is very difficult to

implement. For this reason, all the experimental

study of meteor burst propagation is based on

indirect measurements only.

That’s why simulation is the only solution. The

simulation makes it easy to enable and disable

various randomizing factors while monitoring

changes in the statistical characteristics of received

signal parameters.

The vast majority of MBC simulation models is

based on simple mathematical models developed in

the 1950-s (McKinley, 1961). These models can’t

simulate complex electrodynamic effects taking

place at the scattering off ionized meteor trails. At

the same time, these effects are vital for the studies

of encryption keys distribution. The KAMET

simulation model (Karpov, 2001) based on rigorous

diffractional theory of radio waves scattering

(Khuzyashev, 1984) includes and adequately

reproduces all necessary effects.

We used the Moscow-Kazan MBC link for the

simulation purposes. The following technical

specifications were used during simulation:

 Link length: 720 km;

 Carrier frequency: f = 50 MHz;

 Transmitted power: P

= 2000 W;

 Required signal-to-noise ratio: 20 dB;

 Threshold level: U

= 0,5 μV (which

corresponds to SNR=20 dB);

 Standard deviation of turbulent wind velocity:

= 25 mps.

5 BASIC RANDOMIZING

FACTORS OF METEOR BURST

CHANNEL

An analysis of meteor radio propagation reveals

following basic randomizing factors in the meteor

burst channel:

1. Random spatial orientation of each meteor trail;

2. Random coordinates M(x,y,z) of the reflecting

point on the meteor trail;

3. Random mass m of meteor particle which

produces the ionized trail;

4. Random moment of occurrence of signal fading

(Weitzen, 1987);

5. Random direction and magnitude of the

turbulent wind velocity blowing in the vicinity

of the reflecting points of meteor trail

(Weitzen, 1987);

6. Channel noise and measurement errors.

We used the Pearson correlation coefficient R

between the adjacent measurements of observable

signal parameter as a measure of randomness. Since

it characterizes statistical relationship between the

parameters of two successively detected meteor

radio reflections, the value of R

can be considered

as an indicator of predictability of generated keys.

We consider the carrier phase φ and propagation

delay τ of received signal as observed random

parameters implied for the key generation.

The τ variable is mainly determined by the

geometric path of received signal:

MBAM )(





(1)

In formula (1) c means speed of light, AM and BM

are the distances between the reflecting point of

meteor trail and communication points of the link.

Therefore, randomness of the τ variable is almost

completely determined only by the second

randomizing factor (random coordinates of the

reflecting point). Factor no.5 also gives a small

contribution. However, the total shift of the

reflecting point made by turbulent winds during

signal detection rarely exceeds 100 m (or several λ).

This is much lesser than the contribution of

geometric path (1), which typically is of hundreds

kilometers or more.

The variable φ consists of two components: the

path length shift (2π·f·τ) and polarization phase shift

added by the scattering of radio wave from a meteor

trail. For this reason, the phase value φ is affected by

greater number of randomizing factors. For example,

factor no. 5 is very significant for the carrier phase

and we should not neglect it. This is due to wind

shift of the reflecting point at several λ leads to large

changes in the carrier phase.

6 SELECTION OF

MEASUREMENTS

During the detection of meteor radio reflection its

amplitude and phase are changing in time. These

SecureKeyDistributionbasedonMeteorBurstCommunications

447

changes are recorded as the Amplitude-Time

Response (ATR) and the Phase-Time Response of

radio reflection, respectively. In fact, only

approximate channel reciprocity is observed for the

meteor burst propagation. Calculations and

experiments show that the Phase-Time Response

(t) recorded in point B is slightly different with

the Phase-Time Response φ

(t) recorded in A. Such

difference occurs due to non-absolute reciprocity of

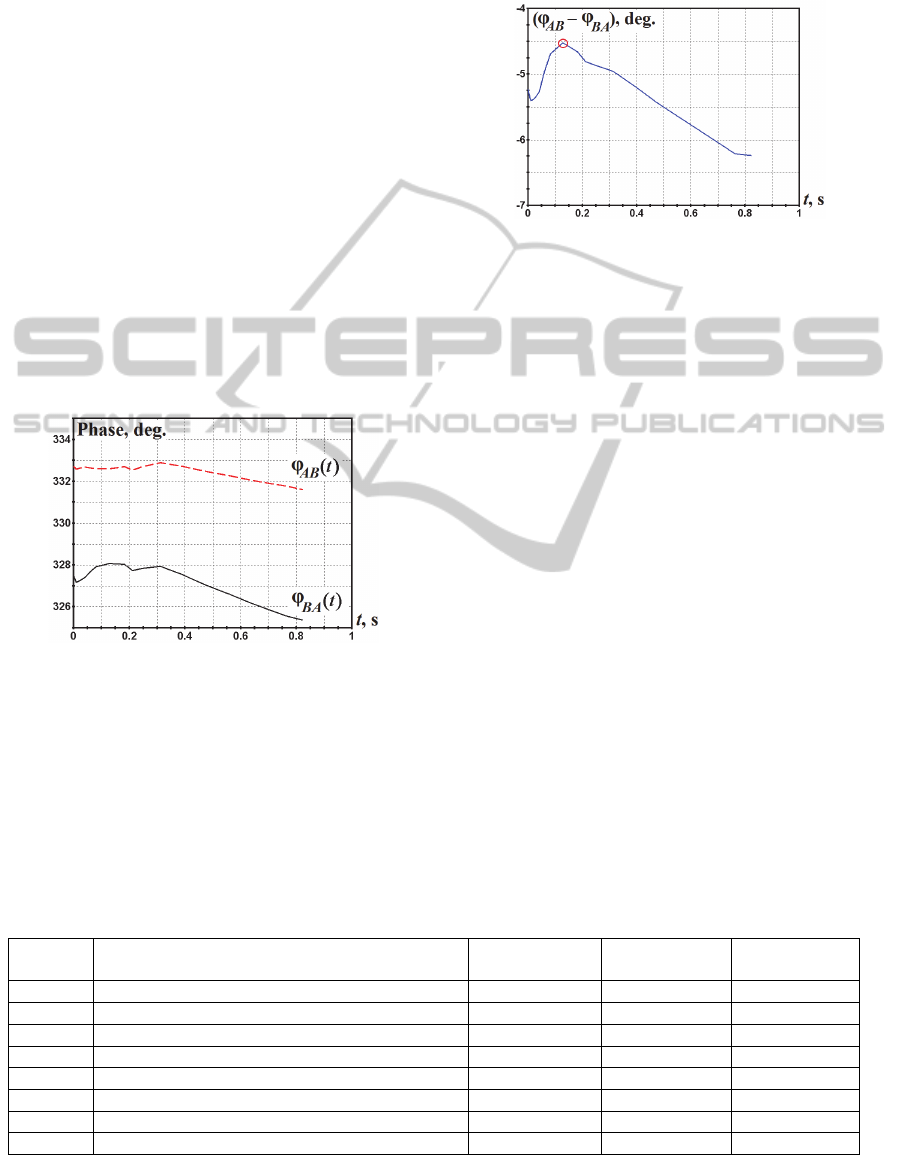
MBC. Figure 1 shows an example of simulated

Phase-Time Responses observed synchronously in

communication points A and B. We should outline

that no noise effect was enabled for these curves.

Figure 2 shows differential PTR for the above

example, which indicates presence of some channel

non-reciprocity. This reciprocity is a consequence of

non-identical scattering of radio waves transmitted

by the opposite communication points. It occurs

every time the reflecting point is located non-

symmetrically relative to the communication points

A and B.

Figure 1: Examples of Phase-Time Responses of the same

meteor radio reflection observed at both sides of the link

The profiles of PTR and differential PTR are

unpredictable and individual for every specific

meteor radio reflection. For the keys generated in

points A and B to be identical, the moment of

minimum absolute value of channel non-reciprocity

should be used to make phase measurements. Such

point (t* = 0.13s) is marked in Figure 2 with a circle.

In this approach, only a single value of the carrier

phase φ and propagation delay τ should be extracted

from each meteor radio reflection.

Figure 2: Example of MBC non-reciprocity.

7 SIMULATION RESULTS

To evaluate significance of various randomizing

factors, a simulation of the test Moscow-Kazan radio

link has been carried out. Step by step, we reduced

the number of randomizing factors at each stage of

the simulation. For each set of randomizing factors a

sample of N = 5000 meteor radio reflections was

simulated. This allowed the points A and B to collect

5000 measurements of the carrier phase φ and

propagation delay τ implied for the key generation

purposes. For each simulated radio reflection a PTR

consisting of M = 2000 points with sampling interval

Δt = t

j+1

– t

= 5ms has been calculated.

The simulation results are summarized in the Table

1. The second column of the table contains short

symbolic notation of enabled ("+") and disabled ("–

") randomizing factors. The symbol ("x") denotes

that this factor is not significant, i.e. its activation

and disabling did not affect at the simulation results.

It was found at the stage no.5 that the factor no. 4

should be classified as non-significant. At the

subsequent stages of simulation this factor was

ignored.

Table 1: Simulation results.

Stage

No.

Enabled randomizing factors

)(

R

)(



R )(

PTRR

1 1+| 2+| 3+| 4+| 5+| 6x 0.015 0.008 0.401

2 1–| 2+| 3+| 4+| 5+| 6x 0.002 0.022 0.407

3 1–| 2+| 3–| 4+| 5+| 6x 0.001 0.004 0.580

4 1–| 2+| 3–| 4+| 5–| 6x 0.013 0.010 0.698

5 1–| 2+| 3–| 4–| 5–| 6x 0.003 0.012 0.690

6 1–| 2–| 3+| 4x| 5+| 6x 0.007 0.011 0.826

7 1–| 2–| 3–| 4x| 5+| 6x 0.010 0.015 0.915

8 1–| 2–| 3–| 4x| 5–| 6x 1.000 1.000 1.000

SECRYPT2014-InternationalConferenceonSecurityandCryptography

448





















)(

(2)

The third and fourth columns of the Table 1

show values of the Pearson correlation coefficient R

between the adjacent measurements of the phase φ

and propagation delay τ. Each of the 5000 simulated

measurements has been selected according to the

selection criterion discussed in the section 6. The

simulation results show that the samples of phase

and propagation delay measurements remain to be

random up to exclusion of all the MBC randomizing

factors. Therefore, the values in the third and fourth

columns do not allow indication of the significance

of individual randomizing factors.

To get more indicative measure of statistical

relationship between the successively detected

meteor radio reflections, we should consider a

correlation between the whole Phase-Time

Responses but not the correlation between their

single counts, as we did before. The R

(PTR) values

calculated according to the formula (3) are presented

in the last column of the Table 1.







































)()(

)(

jiji

PTRR

(3)

At the first and the second simulation stages the

mass m of meteor particles was a random variable

with the inverse-power probability distribution. At

the third stage masses of all the simulated meteor

particles were fixed at value m = 5·10

-4

g. The same

value was also used at the simulation stages no. 4, 5,

7 and 8.

The simulation showed that the factor no. 2

“random coordinates M(x,y,z) of the reflecting

point” is the most significant randomizing factor in

meteor burst channel. Even if all the simulated

meteor trails have the same spatial orientation (i.e.

factor no. 1 is disabled) there is still a great

randomness in the characteristics of received signal

due to presence of the factor no. 2. This allows

considering the factor no. 2 as the most basic

randomizing factor. As it can be traced out from the

last column of the Table 1, the shapes of Phase-Time

Responses for the successively detected meteor

radio reflections are becoming mostly identical as

we reduce the number of enabled randomizing

factors.

The simulation also showed that the Phase-Time

Response of radio reflection produced by an

underdensed meteor trail typically has a smooth

shape with no sharp phase discontinuities.

Conversely, the Phase-Time Response of radio

reflection produced by an overdensed meteor trail

typically reveals much more intensive variation of

the carrier phase in time. In other words, the phase

measurements produced by the overdensed meteor

trails are more stochastic.

8 CONCLUSIONS

Based on the simulation results, we can rank the

randomizing factors of meteor burst channel in order

of their significance as follows:

1) Random coordinates M(x,y,z) of the reflecting

point on the meteor trail (factor 2);

2) Random spatial orientation of each meteor trail

(factor no. 1);

3) Random direction and magnitude of the

turbulent wind velocity blowing in the vicinity

of the reflecting points of meteor trail (factor

no. 5);

4) Random mass m of meteor particle which

produces the ionized trail (factor no. 3);

5) Random moment of occurrence of signal fading

(factor no. 4);

6) Other randomizing factors.

Enabling the factors no.1, 2 and 5 ensures

unpredictability of the carrier phase φ and

propagation delay τ of received signal. No any

immediate influence of the number of enabled

randomizing factors on the statistical and

probabilistic properties of observed random

variables have been identified during the simulation.

The only exception is the factor no. 2, which is the

most basic in randomizing the observed parameters

of received signal. It was also found that the factor

no. 4 barely affects on the probabilistic and

statistical properties of observed variables.

Radio reflections produced by the overdensed

meteor trails have less predictable variations of the

signal amplitude and phase. However, a serious

drawback of the overdensed trails is a higher value

of the channel non-reciprocity. Rise of the channel

non-reciprocity results in a higher probability of bit

mismatch between the keys generated by Alice and

Bob. Thus, the use of radio reflections produced by

the overdensed trails provides higher entropy of

SecureKeyDistributionbasedonMeteorBurstCommunications

449

encryption key but reduces a key generation rate due

to increased channel non-reciprocity.

The future research work should be aligned at the

performance evaluation and security analysis of the

meteor cryptography systems. Non-reciprocity

effects of meteor radio propagation and spatial

correlation features of meteor burst channel should

be considered to address the above problems.

REFERENCES

Bennett, C., Brassard, G., 1984. Quantum Cryptography:

Public key distribution and coin tossing. In

Proceedings of IEEE International Conference on

Computers, Systems and Signal Processing

(Bangalore, India), pp. 175-179.

Desourdis, R.J., Wojtaszek, H., Sidorov, V.V. et el., 1993.

Nonreciprocity of Meteor Scatter Radio Links. In

IES’93, Proceedings of Ionospheric Effects

Symposium, pp. 165-173.

Hershey, J.E., Hassan, A.A., Yarlagadda, R., 1995.

Unconventional cryptographic keying variable

management. In IEEE Transactions on

Communications, vol.43., iss.1, pp.3-6.

Karpov, A., Tereshin, S., Abrosimov, J., 2001. The

computer model “KAMET”: The new generation

version. In Proceedings of the Meteroids 2001

Conference (Kiruna, Sweden, 6-10 August 2001),

pp.367-370.

Karpov, A.V., Sidorov, V. V., 2005. Method for

protecting information in meteor radio channel by

encryption by random natural occurrence. Russian

Federation Patent No. RU 2265957, published at

10.12.2005 in Bull. 34

Khuzyashev, R.G., 1984. Calculation of the amplitude and

phase characteristics of a signal scattered obliquely off

a meteor trail. In Radiophysics and Quantum

Electronics, vol. 27, iss.9, pp. 778-782.

Korneyev, V.A., Epictetov, L.A., Sidorov, V. V., 2003.

Time & Frequency coordination using unsteady,

variable-precision measurements in meteor burst

channel. In Proceedings of 17th European Frequency

and Time Forum (Tampa, USA), 4-8 May.

Korneyev, V.A., Sidorov, V.V., 2007. Optimization of

concurrent data and high-precision time transfer

modes in meteor burst synchronization equipment. In

TimeNav’07, Proceedings of 21st European

Frequency and Time Forum, pp. 923-926.

Madiseh, M.G., McGuire, M. L., Neville, S. S., Cai L.,

2008. Secret key generation and agreement in UWB

communication channels. In GLOBECOM 2008,

Proceedings of the IEEE Global Telecommunications

Conference, pp.1-5.

Madiseh, M.G., He, S., McGuire, M.L., Neville, S. W.,

Dong, X., 2009. Verification of secret key generation

from UWB channel observations. In ICC’09,

Proceedings of the IEEE International Conference on

Communications, pp. 593-597.

Mathur, S., Trappe, W., Mandayam, N., Ye, C., Reznik,

A., 2008. Radio-Telepathy: extracting a secret key

from an unauthenticated wireless channel. In

MobiCom’08, Proceedings of the 14th ACM

international conference on Mobile computing and

networking, pp. 128-139.

McKinley, D.W.R., 1961. Meteor science and

engineering, McGraw-Hill, 309 p.

Sidorov, V.V., Epictetov, L.A., 1993. Application of

Meteor Burst Equipment for High Precision

Comparisons of Time and Frequency Standards. In

EFTF’93, Proceedings of 7th European Frequency

and Time Forum, pp. 413-416.

Sidorov, V.V., Karpov, A.V., Korneev, V.A., Nasyrov,

A.F, 2007. Meteor Time Transfer and Meteor

Cryptography. In TimeNav’07, Proceedings of 21st

European Frequency and Time Forum, pp. 315-317.

Weitzen, J.A., Sowa, M., Scofidio, R., Quinn, J., 1987.

Characterizing the Multipath and Doppler Spreads of

the High-Latitude Meteor Burst Communication

Channel. In IEEE Trans. on Comm., vol.35, pp.1050-

1058.

SECRYPT2014-InternationalConferenceonSecurityandCryptography

450