Optimal Walking of an Underactuated Planar Biped

with Segmented Torso

Zhongkai Chen

, Naﬁssa Lakbakbi El Yaaqoubi

and Gabriel Abba

LCFC, Arts et M´etiers ParisTech, 4 rue Augustin Fresnel, 57078 Metz Cedex 3, France

ENIM, 1 rue Ars Laquenexy, 57078 Metz Cedex 3, France

Keywords:

Biped Robot, Optimal Walk, Segmented Torso, Zero Dynamics, Energy Efﬁciency.

Abstract:

Recently, underactuated bipeds with pointed feet have been studied to achieve dynamic and energy efﬁcient

robot walking patterns. However, these studies usually simplify a robot torso as one link, which is different

from a human torsos containing 33 vertebrae. In this paper, therefore, we study the optimal walking of a 6-link

planar biped with a segmented torso derived from its 5-link counterpart while ensuring that two models are

equivalent when the additional torso joint is locked. For the walking, we suppose that each step is composed

of a single support phase and an instantaneous double support phase, and two phases are connected by a

plastic impact mapping. In addition, the controlled outputs named symmetry outputs capable of generating

exponentially stable orbits using hybrid zero dynamics, are adopted to improve physical interpretation. The

desired outputs are parameterized by B´ezier functions, with 5-link robot having 16 parameters to optimize

and 6-link robot having 19 parameters. According to our energy criterion, the segmented torso structure may

reduce energy consumption up to 8% in bipedal walking, and the maximum energy saving is achieved at high

walking speeds, while leaving the criteria at low walking speeds remain similar for both robots.

1 INTRODUCTION

One of the fundamental tasks in designing biped

robots is to ﬁnd robot structures and control strategies

capable of providing energy-efﬁcient and stable

walking motions. As indicated in Figure 1, many

researchers have tried to study the energy saving

beneﬁts of bionic robot designs by adopting certain

human resembling parts such as curved feet (Martin

and Schmiedeler, 2012), rolling knees (Hobon et al.,

2013), locked knees (Sinnet et al., 2011), swinging

arms (Kaddar et al., 2012) or springs (Bauer et al.,

2014). Nevertheless, the theoretical advantages of a

human-like robot torso are still rarely studied among

the vast literature on humanoid robots, despite the

studies on realizing human-like biped torsos from a

practical point of view (Mizuuchi et al., 2006).

Unveiling the theoretical advantages of humanlike

robot structures requires numerical optimization. By

far, the most common method is through designing

reference trajectories with a limited number of

parameters, whether the trajectories are functions of

time or functions of robot state, and then optimizing

these parameters using a certain cost function. Many

researchers have used optimization in the analysis

Curved feet

Underactuation

Rolling knees

Knee-locking

Swinging arms

Springs and dampers

Segmented torso

Compliant torso

Figure 1: Possible methods for reducing energy

consumption.

and design of biped walking motions with trajectories

deﬁned as functions of time (Cabodevila and Abba,

1997; Chevallereau and Aoustin, 2001; Beletskii

et al., 1982), and these early studies usually adopted

the zero moment point (ZMP) principle to ensure the

feasibility of various walking motions. However, a

periodic and feasible walking motion might not be

stable because biped robots are hybrid systems with

impacts during each step, which might serve as a

discrete positive feedback of error. Some researchers

also attempted to eliminate the impact completely

and thus creating walking motions that consume no

213

Chen Z., El Yaaqoubi N. and Abba G..

Optimal Walking of an Underactuated Planar Biped with Segmented Torso.

DOI: 10.5220/0005115702130220

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 213-220

ISBN: 978-989-758-040-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

mechanical energy, but these studies are only valid for

passive biped robots walking in a highly controlled

environment (Rouhollah et al., 2013). For activated

robots with motors, it’s practically impossible to

eliminate the energy consumption caused by Joule

heating.

Recently, with more and more researchers striving

to achieve more dynamic biped walking patterns, a

planar biped robot with pointed feet and the name

“RABBIT” was created, which witnessed the birth of

the concept called “virtual constraints” (Chevallereau

et al., 2003). By using a monotonic scalar quantity

representing the progression of a step, Westervelt

and Grizzle (2002) proposed a method to deﬁne

trajectory functions with a closed-form stability

indicator. Armed with this method, Ames (2012)

proposed human outputsto relate the walking motions

of biped robots to the human walking data collected

in a laboratory.

The work presented here is inspired by both

the previously studied human-like parts and the

optimization methods with provable stability. Our

intention is to analyze the energy-saving potentials of

the segmented torso. The optimal walking of a 5-link

robot and a 6-link robot with underactuated pointed

feet is studied to quantify the difference between

these two robot conﬁgurations. The segmented torso

of the 6-link robot is assumed to be straight at the

beginning and the end of each step. Based on the

stability analysis proposed by Westervelt and Grizzle

(2002), we deﬁne symmetry outputs to observe the

mirror-like behavior of a virtual stance leg and a

virtual swing leg. This interpretation of bipedal

walking motions is related to a previous research

on asymptotic stable walking with simpliﬁed posture

control and swing leg advancement strategies (Grizzle

et al., 2001). By running optimization with symmetry

outputs at different walking speeds, we have found

obvious energy efﬁciency improvement of the 6-link

robot compared with its 5-link rival, especially at high

walking speeds.

The paper is structured as follows. Section 2

delineates the biped models of both 5-link and 6-link

robots. Section 3 introduces the symmetry outputs

together with the feedback design using optimized

HZD. Section 4 deals with the optimization problem

using B´ezier trajectories with provable stability.

Section 5 presents the optimized walking motions of

the two biped robots at different speeds. Finally,

Section 6 concludes this paper by discussing the

advantage of the additional torso joints and possible

subsequent studies.

2 ROBOT MODELS

2.1 Robot Parameters

Both 5-link robot and 6-link robot have pointed feet

which are not actuated during each step, and the rotor

inertias are the same for all the actuators. As shown

in Figure 2, the 5-link robot analyzed here comprises

one torso, two femurs and two tibiae. We assume

that all links are considered rigid and the motion is

constrained to the sagittal plane.

(x,y)

Figure 2: 5-link planar biped robot.

The 6-link robot, depicted in in Figure 3, is

derived from the 5-link robot, and the only difference

is that the additional torso joint divides the torso

into an upper torso and a lower torso. In order to

compare the performance of both robots, the 6-link

robot should be equivalent to its 5-link counterpart

once the additional joint is locked. This is realized

by the following equations

= M

+ M

(1)

= M

+ M

+ p

) (2)

+ M

− p

)

+ I

+ M

− p

)

(3)

where the notations used above is explained in

Table 1. For the actuators of the femurs and tibiae,

the rotor inertias equal 0.83 kgm

, and the motor rotor

inertia of the additional torso joint is 0.2 kgm

2.2 Dynamic Models

The generalized coordinate vector describing both

biped robots in the sagittal plane is deﬁned as q

[x,y,q

,...,q

]

′

where n = 5 or 6 equaling the

number of links. It contains two coordinates (x and

y) describing the position of pelvis and n angles q =

,...,q

]

′

for the orientation of legs and torsos.

We assume that the positive angles are anticlockwise.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

214

Table 1: Model Parameters for 5-link Robot and 6-link Robot.

Common 5-link 6-link

Model Parameters Femurs(f) Tibia(t) Torso(T) Lower Torso(T1) Upper Torso(T2)

Mass,M

∗

(kg) 6.8 3.2 17.1 10 7.1

Length,L

∗

(m) 0.4 0.4 0.625 0.3 0.325

Inertia,I

∗

kg) 0.0693 0.0484 0.562 0.115 0.075

Mass Center,p

∗

(m) 0.163 0.127 0.224 0.1 0.1

, I

(x,y)

Figure 3: 6-link planar biped robot.

The dynamic model of the biped robot is divided

into two models: the swing phase model and the

impact model. Using the Euler-Lagrange equations,

one obtains the swing phase models of the form

D(q) ¨q+C(q, ˙q) + G(q) = Bu (4)

where the matrix D is the inertia matrix, C is the

(n × 1) vector of Coriolis terms, G is the (n × 1)

vector of gravity terms, and B maps the joint torques

to generalized forces.

An impact occurs when the swing leg end hits the

ground. We assume that the impact is plastic, and the

relabeling of robot’s coordinates after each impact is

also included in the impact model. Let x = [q, ˙q]

′

the state variables of the robot. The impact model can

be formulated as

= ∆(x

−

) =



∆

−

∆

˙q

−

) ˙q

−



(5)

where ∆

is a relabeling function, ∆

˙q

−

) is a n × n

matrix, x

= [q

, ˙q

]

′

and x

−

= [q

−

, ˙q

−

]

′

(Westervelt

and Grizzle, 2002).

The overall model of walking is obtained by

combining the swing phase model and the impact

model to form a hybrid model. Assuming that the

evolution of the swing phase model possesses ﬁnite

left and right limits, one can denote them by x

−

(t) =

lim

τ→t

− x(τ) and x

(t) = lim

τ→t

+ x(τ), respectively.

The hybrid model can then be formulated as

Σ :

(

˙x = f(x) + g(x)u x 6∈ S

= ∆(x

−

) x

−

∈ S

(6)

where S = {(q, ˙q)|h

(q) = 0,dh

(q) ˙q < 0} is the

switching surface.

Converting the dynamic equation (4) to a ﬁrst

order ODE, f(x) and g(x) can be calculated as

f(x) =



˙q

−D

−1

(q)(C(q, ˙q) + G(q))



(7)

g(x) =



5×4

−1



(8)

3 OUTPUTS AND FEEDBACK

3.1 Symmetry Outputs

Depending on the robot model one chooses, the

dimension of the output equals to (n − 1), and an

almost linear output function can be deﬁned as

y = h(q) = h

(q) − h

◦ θ(q) (9)

where h

(q) represents independent controlled

quantities and h

◦ θ(q) represents the ideal evolution

of these quantities as a function of the scalar quantity

θ(q) (Westervelt et al., 2007). θ(q) is a strictly

monotonic function of the robot’s state, and it is

used to replace time in parameterizing periodic biped

motion. If the virtual stance leg is deﬁned as the line

connecting both the stance hip and the stance foot,

then its opposite angle in the sagittal plane will be

monotonically increasing. Since the lengths of the

femurs and the tibiae are equal, θ can be formulated

for both robots as

θ(q) = cq = −q

− q

/2− q

(10)

where the minus signs are adopted to make θ strictly

increasing.

Intuitively, there are two tasks to achieve in

bipedal walking: posture control and swing leg

advancement. Posture control is to maintain the

torso in an almost upright position, while swing leg

advancement deals with commanding the swing leg

to pass beyond the stance leg and ensuring a desired

step length. For a compass gait robot with no ankles

and no knees, the simplest version of posture control

is to maintain torso at some constant value, and

OptimalWalkingofanUnderactuatedPlanarBipedwithSegmentedTorso

215

the simplest version of swing leg advancement is to

command the swing leg to behave as the mirror image

of the stance leg (Grizzle et al., 2001). Inspired by the

physical interpretation of these methods, we deﬁne h

of the 5-link robot as follows

(q) = H

q = [θ

symm

]

′

(11)

symm

/2+ q

/4+ q

+ q

/4+ q

+ π

(12)

where θ

symm

describes the mirror-like behavior of the

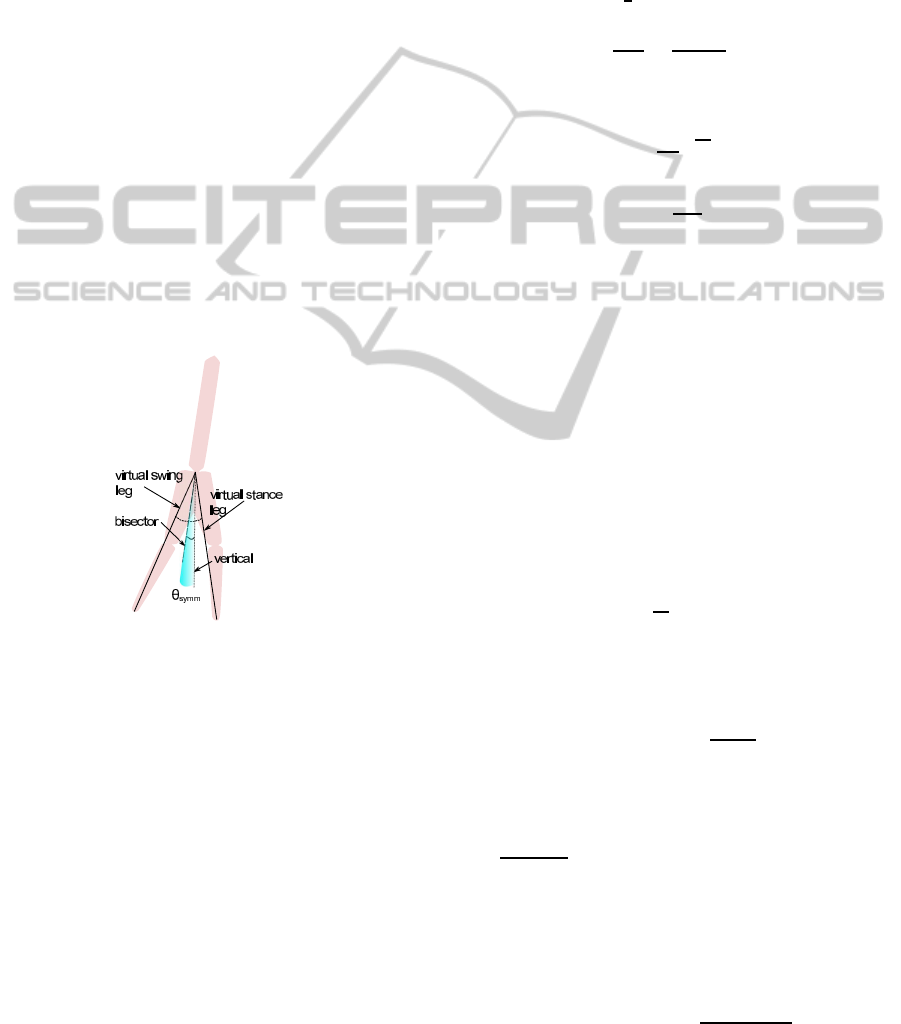
virtual swing leg with regard to the virtual stance leg.

As shown in Fig.4, it can be interpreted physically

as the angle between the bisector of virtual swing leg

and virtual stance leg and the gravity direction. q

the absolute angle of the torso, which is responsible

for posture control. q

and q

are the angles of the

stance knee and the swing knees. Since the outputs

have the same proportion of quantities from the stance

leg (q

, q

) and the swing leg (q

, q

), it is named

as “Symmetry Ouputs”. As for h

, its deﬁnition is

related to speciﬁc feedback designs, which will be

discussed in the next section. For 6-link robot, the

deﬁnition of θ

symm

is the same, but h

(q) need to be

replaced by [θ

symm

]

′

Figure 4: Geometric interpretation of symmetry outputs.

3.2 Feedback Design using HZD

Assuming that h

is deﬁned by trajectory functions of

θ(q) and the invariance of the impact map is satisﬁed,

the goal of the feedback design with optimized HZD

is to keep the robot evolution on the zero dynamic

surface. The method of explicitly constructing the

zero dynamics already exists, and we brieﬂy list all

the equations with the same labeling system in the

context of our robot conﬁguration so as to achieve

logical completion (Westervelt et al., 2003). The

following equations can be used in calculating zero

dynamics for both the 5-link robot and the 6-link

robot.

Because of the speciﬁc choice of h

(q), one can

express the zero dynamics as

= θ(q)

= γ(q, ˙q)

(13)

where θ(q) is deﬁned by (10) and γ(q, ˙q) can be

explicitly computed to be the ﬁfth entry of D(q) ˙q. The

hybrid zero dynamics is originally 2-dimensional, and

it can be equivalent to a 1-dimensional discrete time

dynamical system when the hyperplane ξ

= θ

−

chosen as the Poincar´e section and the coordinate

transformation ζ

(ξ

)

is adopted, yielding

dζ

dξ

(ξ

)

(ξ

)

(14)

where κ

(ξ

) and κ

(ξ

) are given by

(ξ

) =

∂θ

∂q



∂h

∂q



−1







(15)

(ξ

) = −

∂V

∂q



(16)

with V(q) the potential energy of the biped, γ

= D

(the ﬁfth row of D) and ∂V/∂q

= G

(the ﬁfth row of

G(q)).

The zero dynamic representation enables us to

determine the existence and stability of a ﬁxed point

of the zero dynamics without integrating the ODE

(Westervelt et al., 2007). To begin with, the relation

between ξ

−

and ξ

can be calculated by

= δ

zero

−

(17)

where δ

zero

intricately determines the stability of a

limit cycle in the zero dynamics surface and can be

computed in advance as

zero

= γ

)∆

˙q

−

)σ

˙q

−

) (18)

˙q

−

) =



∂h

∂q

−

)

−

)



−1





(19)

Thus the potential energy of the zero dynamics (13)

becomes

zero

(ξ

) = −

(ξ)

dξ (20)

which can determine whether the biped will take a full

step by judging if

zero

1− δ

zero

(θ

−

) + K < 0,(δ

zero

6= 0) (21)

where K = maxV

zero

(ξ

) with θ

≤ ξ

≤ θ

−

Furthermore, if 0 < δ

zero

< 1 also holds, there

exists an exponentially stable periodic orbit with the

ﬁxed point being

∗

= cq

−

,ζ

∗

−V

zero

(θ

−

)

1− δ

zero

(22)

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

216

Given ξ

∗

and ζ

∗

, ξ

(ξ

,ζ

∗

) can be further calculated

(ξ

,ζ

∗

) = −

2(δ

zero

∗

−V

zero

(ξ

)) (23)

Then q(t) and ˙q(t) are given by

q =





−1



(ξ

)



(24)

˙q =



∂h

∂q



−1





(25)

and the torque u(x) is attained through

u(x) = −(L

h(q, ˙q))

−1

h(q, ˙q) (26)

In addition, t(ξ

) can be calculated as

t(ξ

) =

−

(ξ

)ξ

(ξ

,ξ

−

)

dξ

(27)

4 OPTIMAL WALKING MOTION

4.1 Parameterization of h

B´ezier polynomials are widely adopted in

parameterizing underactuated biped robots because

they do not display large oscillations with small

parameter variations and they can easily achieve

impact invariance (Westervelt et al., 2007).

To facilitate calculation, we start by normalizing

the previously deﬁned θ(q) as

s(q) =

θ(q) − θ

−

− θ

(28)

with θ

the minimum value of θ(q) and θ

−

the

maximum value of θ(q). Then h

◦ θ(q) can be

deﬁned as

◦ θ(q) = B

◦ s(q) (29)

where B

= [b

,...b

n−1

]

′

with n being the number of

links as before. Each b

is further deﬁned by

(s) =

∑

k=0

k!(5− k)!

(1− s)

5−k

(30)

which is a B´ezier polynomial of degree 5. Group the

parameters a

into vectors as a

= (a

,...,a

n−1

and we can calculate a

directly from a

using





= H∆

−1



−



(31)

where H = [H

′

]

′

. Moreover a

can also be

calculated once a

and a

are available simply by

using

−

− θ

5c˙q

˙q

+ a

(32)

where ˙q

−

= σ

˙q

−

) and ˙q

= ∆

˙q

−

) ˙q

−

Thus the parameter set {a

} is able to

determine h

for both the 5-link and 6-link robot.

For the 5-link robot, the parameter set contains 16

parameters. As for the 6-link robot, the torso has the

tendency to bend down signiﬁcantly at high walking

speeds, which impairs its resemblance to real human

torsos. In order to avoid excessive curvy torsos, we

assume that the initial shape of the segmented torso is

straight (q

−

= 0), meaning that there will be one less

parameter to optimize. Therefore, the parameter set

of the 6-link robot is composed of 19 parameters.

4.2 Cost Function

For the system (6), the output (9) is deﬁned by h

and θ as in (10), (11) and (29). The optimization

requires one to ﬁnd an appropriate cost function. For

biped robots with electrical motors, the major energy

consumption is caused by Joule effect, and thus the

cost function should be proportional to this loss of

energy. It is deﬁned as the integral of the norm of

the torque for a displacement of one meter

C =

N−1

∑

i=1

∗

(t))

dt (33)

where T is the step duration, and d

corresponds to

step length. The cost function can also be written as

(Westervelt and Grizzle, 2002)

C =

−

∑

N−1

i=1

∗

(ξ

,ξ

))

(ξ

)ξ

(ξ

,ξ

−

)

dξ

(34)

4.3 Constraints

The constraints in the optimization problem is

adopted to ensure the validity of the optimal

trajectory. For both robot conﬁgurations, the

constraints include:

• The ground reaction acting on the stance leg

end should always be larger than 50N, and the

maximum ratio of tangential to normal ground

reaction forces should be less than the friction

coefﬁcient, which is 0.6 in our case.

• The impulsive impact force must be upward and

conform to the friction coefﬁcient. The post-

impact velocity of the swing leg tip is upward.

• The swing leg end must not touch the ground

before the end of one periodic step.

• The existence of a ﬁxed point needs ξ

∗

> K/δ

zero

and the stability of the ﬁxed point, 0 < δ

zero

< 1.

• The average walking speed, v = d/T.

OptimalWalkingofanUnderactuatedPlanarBipedwithSegmentedTorso

217

4.4 Optimization Method

The above procedure can be performed using

MATLAB Optimization toolbox, which provides

different optimization methods such as Nelder-Mead,

sequential quadratic programming (SQP), and active

set. Among them, we have chosen SQP as

our optimization method for its superior capability

in handling the situation where the cost function

cannot provide the criterion due to the violation of

certain constraints such as the constraint ensuring the

existence of a ﬁxed point.

5 RESULT ANALYSIS

As the stability of the hybrid zero dynamics is well

deﬁned, we no longer need to use simulation to prove

the stability of the walking. In order to compare

the energy efﬁciency between the 5-link robot and

6-link robot, we have run optimization at various

speeds ranging from 0.25m/s to 1.5m/s. As depicted

in Figure 5, the torque costs of the two biped robots

are almost the same at the walking speed from

0.25m/s to 1.2m/s. As the walking speed continues to

increase, the advantage of the 6-link robot in energy

efﬁciency becomes more and more obvious. The

similar results were also obtained in biped robots with

modest swinging arms, but their method is based on

ZMP theories and thus do not provide solid proof of

stability (Kaddar et al., 2012).

At 1.5m/s, the torque cost of the 6-link robot is

almost 8% less than that of its counterpart. The stick

diagrams of the both robots walking at this speed are

illustrated in Figure 6 and Figure 7 respectively, and

the friction requirementsfor both walking motions are

satisﬁed according to Figure 8. The torque charts for

0 0.5 1 1.5

500

1000

1500

2000

2500

3000

3500

4000

speed [m/s]

criterion [N

ms]

5−link 6−link

Figure 5: The torque cost versus walking speed for both

biped robots.

−0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8

0.5

1.5

Figure 6: The optimal walking motion of the 5-link robot at

1.5m/s.

−0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8

0.5

1.5

Figure 7: The optimal walking motion of the 6-link robot at

1.5m/s.

all the actuators are shown in Figure 9. We can see

that the gaits of these two robots are quite similar.

As shown in Table 2, the additional torso joint do

consume energy, but on the whole the 6-link robot

is still more energy efﬁcient because of the reduced

torque costs at the other joints, especially at the swing

hip. The angle charts describing the movement of

both robots are shown in Figure 10. We can ﬁnd

that the ﬂuctuation of q

and θ

symm

, for both robots,

is comparatively mild compared with all the other

angles. The intuitive justiﬁcation for it would be that

the torso rotation is limited during one step and the

virtual swing leg behave approximately as the mirror

image of the virtual stance leg.

6 CONCLUSIONS

The advantage of using a segmented torso instead of a

one-piece torso is studied in this paper. According to

the current optimization results, the 6-link biped robot

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

218

Table 2: Energy Costs at 1.5m/s.

Energy Costs (N

ms)

Robot Type Stance Hip Stance Knee Swing Hip Swing Knee Torso Joint Total

5-link 1634 364.7 1579 314.5 - 3893

6-link 1689 266.0 1301 269.2 64.8 3590

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

−50

100

150

200

250

300

350

Force [N]

Time [s]

(5−link)

(6−link)

Figure 8: The ground reaction forces versus time.

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

−50

100

150

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

−20

Torque [Nm]

(5−link) u

(6−link) u

(6−link)

(5−link) u

(6−link) u

(6−link)

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

Time [s]

(6−link)

Figure 9: The applied torques versus time.

with segmented torso consumes less energy than its

5-link counterpart at high walking speeds, and the

improvement is mainly due to the reduced torque cost

at the swing hip. The results are purely theoretical

since there is no platform capable of testing 6-link

biped with the additional torso joint at present, but

we will try to attain related experimental data in

the future. In addition, there may still be room

for further reducing the energy criterion because the

current hypotheses of the additional torso joint is

still different from the semi passive nature of a real

human torso. Therefore, our future study will focus

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

−2.8

−2.6

−2.4

−2.2

−2

−1.8

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

−0.6

−0.4

−0.2

Angle [rad]

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

−0.58

−0.56

−0.54

−0.52

−0.5

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

−0.1

0.1

0.2

Time [s]

(5−link) q

(6−link) q

(6−link)

(5−link) q

(6−link) q

(6−link)

(5−link) q

(6−link)

symm

(5−link)

(6−link)

symm

(6−link)

Figure 10: The angles versus time.

on exploring the effect of a passive segmented torso

on the energy efﬁciency of walking motion.

ACKNOWLEDGEMENTS

This work was supported by China Scholarship

Council (CSC, No. 201206260112). We would like

to thank Fabian Bauer and Christine Chevallereau for

valuable advises concerning optimization procedures.

REFERENCES

Ames, A. (2012). First steps toward underactuated human-

inspired bipedal robotic walking. In Proceedings

- IEEE International Conference on Robotics and

Automation, pages 1011–1017.

Bauer, F., Fidlin, A., and Seemann, W. (2014).

Energy efﬁcient bipedal robots walking in resonance.

ZAMM - Journal of Applied Mathematics and

Mechanics / Zeitschrift f¨ur Angewandte Mathematik

und Mechanik.

Beletskii, V., Berbyuk, V., and Samsonov, V. (1982).

Parametric optimization of motions of a bipedal

walking robot. Mechanics of solids, 17(1):24–35.

OptimalWalkingofanUnderactuatedPlanarBipedwithSegmentedTorso

219

Cabodevila, G. and Abba, G. (1997). Quasi optimal gait for

a biped robot using genetic algorithm. In Proceedings

of the IEEE International Conference on Systems,

Man and Cybernetics, volume 4, pages 3960–3965.

Chevallereau, C., Abba, G., Aoustin, Y., Plestan, F.,

Westervelt, E., Canudas-de Wit, C., and Grizzle, J.

(2003). Rabit: A testbed for advanced control theory.

IEEE Control Systems Magazine, 23(5):57–79.

Chevallereau, C. and Aoustin, Y. (2001). Optimal reference

trajectories for walking and running of a biped robot.

Robotica, 19(5):557–569.

Grizzle, J., Abba, G., and Plestan, F. (2001).

Asymptotically stable walking for biped robots:

Analysis via systems with impulse effects. IEEE

Transactions on Automatic Control, 46(1):51–64.

Hobon, M., Elyaaqoubi, N., and Abba, G. (2013). Gait

optimization of a rolling knee biped at low walking

speeds. In ICINCO 2013 - Proceedings of the 10th

International Conference on Informatics in Control,

Automation and Robotics, volume 2, pages 207–214.

Kaddar, B., Aoustin, Y., and Chevallereau, C. (2012).

Arms swing effects on a walking planar biped. In

ASME 2012 11th Biennial Conference on Engineering

Systems Design and Analysis, ESDA 2012, volume 3,

pages 293–301.

Martin, A. and Schmiedeler, J. (2012). The effects of curved

foot design parameters on planar biped walking.

In Proceedings of the ASME Design Engineering

Technical Conference, volume 4, pages 815–824.

Mizuuchi, I., Yoshikai, T., Sodeyama, Y., Nakanishi, Y.,

Miyadera, A., Yamamoto, T., Niemel¨a, T., Hayashi,

M., Urata, J., Namiki, Y., Nishino, T., and Inaba, M.

(2006). Development of musculoskeletal humanoid

kotaro. In Proceedings - IEEE International

Conference on Robotics and Automation, volume

2006, pages 82–87.

Rouhollah, J., Louis, L., Aren, H., and Ranjan, M. (2013).

Energy-conserving gaits for point-foot planar bipeds:

A ﬁve-dof case study. In ASME 2013 Dynamic

Systems and Control Conference.

Sinnet, R., Powell, M., Shah, R., and Ames, A. (2011).

A human-inspired hybrid control approach to bipedal

robotic walking. In IFAC Proceedings Volumes (IFAC-

PapersOnline), volume 18, pages 6904–6911.

Westervelt, E. and Grizzle, J. (2002). Design of

asymptotically stable walking for a 5-link planar

biped walker via optimization. In Proceedings

- IEEE International Conference on Robotics and

Automation, volume 3, pages 3117–3122.

Westervelt, E., Grizzle, J., and Koditschek, D. (2003).

Hybrid zero dynamics of planar biped walkers. IEEE

Transactions on Automatic Control, 48(1):42–56.

Westervelt, E. R., Grizzle, J. W., Chevallereau, C., Choi,

J. H., and Morris, B. (2007). Feedback Control

of Dynamic Bipedal Robot Locomotion. Taylor &

Francis LLC, ﬁrst edition.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

220