A Mixed-Integer Mathematical Programming Model for

Integrated Planning of Manufacturing and Remanufacturing Activities

Davide Giglio and Massimo Paolucci

Department of Informatics, Bioengineering, Robotics and Systems Engineering, University of Genova, Genova, Italy

Keywords:

Remanufacturing, Production Planning, Mixed-Integer Programming Modelling.

Abstract:

This paper considers a hybrid remanufacturing and manufacturing system on a closed-loop supply chain.

The system manufactures a set of new products characterized by a multi-level structure through multi-stage

assembly operations. The required raw or basic parts can be acquired new from suppliers or provided as new

by a de-manufacturing facility which performs a remanufacturing process from acquired old products returned

by customers. The quality of returned products has impact on the quantity of recovered basic parts which can

be assumed as good as new, and on the duration of the remanufacturing process. The considered problem

is to determine the production lots for the system machines as well as the quantity of new basic parts and

retuned products to be acquired in order to satisfy a deterministic demand in the time buckets of the planning

period. The performance criterion to be minimized includes the acquisition costs for the new and returned

items, inventory and production costs, recovering and disposal costs, and tardiness costs. A mixed-integer

programming model is proposed and its effectiveness is demonstrated by experiments on a case study.

1 INTRODUCTION

In the recent years, both academic and practitioner

interest has been focused on closed loop or reverse

logistic supply chain management (Guide Jr. and

Van Wassenhove, 2009), due to the increasing atten-

tion given to environmental issues, in particular rel-

evant to the depletion of natural resources, as well

as the new environmental legislations and economic

concerns. In this connection, the increasing aware-

ness of customers for environmentalsustainable prod-

ucts also drives industries to adapt their resource con-

sumption and supply strategies.

For these reasons, product recovery became a rel-

evant factor that must be appropriately managed in

closed loop supply chains, both at planning and op-

erational level (Guide Jr., 2000). In general, product

recovery consists in several alternative options aim-

ing at exploiting end-life ﬁnished products returned

from customers, so drastically reducing the ﬂow of

such items to land-ﬁll or incineration (Thierry et al.,

1995). In particular,returned products can be repaired

or refurbished to be reintroduced in the market, as

well as remanufactured (several example can be found

in (Fleischmann et al., 1997)). With remanufactur-

ing, old products are disassembled in order to recover

reusable components and materials so that they can be

used for new product fabrication (Zhang et al., 2004).

In this paper, a remanufacturing and manufac-

turing system is considered. The system produces

several kinds of ﬁnished products from the assem-

bly of new or recovered basic parts, which can be

made available from a disassembly process. Specif-

ically, the planning of manufacturing and remanufac-

turing activities must be determined in order to sat-

isfy the demand of ﬁnished products over a speciﬁed

planning horizon. The production is performed by

a set of machines or production lines that are dedi-

cated to the execution of the different phases of the

production cycle of products, whereas a single de-

manufacturing facility is assumed through which the

returned products are disassembled into raw or basic

parts that are restored to as-new state. Usable raw

parts provided by the disassembly process are stored

in inventory together with new parts that are acquired,

whereas not usable ones are sent to disposal. Re-

turned products can be acquired at a cost depending

on their quality level; this latter, in turn, inﬂuences

the number of obtainable recovered raw/basic parts

but not their quality that is assumed equivalent to that

of new parts (Lund, 1985). The planning is performed

at an aggregate level on daily or weekly time buckets,

so that only production capacity restrictions are taken

into account, whereas setups for the machines are not

751

Giglio D. and Paolucci M..

A Mixed-Integer Mathematical Programming Model for Integrated Planning of Manufacturing and Remanufacturing Activities.

DOI: 10.5220/0005118007510759

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 751-759

ISBN: 978-989-758-040-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

RETURNED

PRODUCTS

COLLECTED

PRODUCTS

BASIC

PARTS

FINISHED

PRODUCTS

END USERS /

CONSUMERS

NEW BASIC PARTS

MANUF.REMANUF.

OPERATIONSOPERATIONS

MANUFACTURING SYSTEM

REMANUFACTURING SYSTEM

Figure 1: The system model.

explicitly considered. The demand of ﬁnished prod-

ucts in the time buckets of the planning horizon is as-

sumed known and an upper bound on the number of

the available returned products is considered. Plans

should minimize costs due to the inventory of basic

parts, semi-ﬁnished and ﬁnished products, as well as

costs for basic parts and returned products acquisi-

tion, for disassembly and production, and for late sat-

isfaction of the demand with respect to the due dates.

The problem faced in this paper then consists in

determining the size of the production lots on the con-

sidered machines, together with the quantities of new

basic parts and returned products to be acquired in the

various time buckets. Dynamic lot sizing problems

without considering product returns have been widely

considered in literature. Recently, in (Teunter et al.,

2006) the dynamic lot sizing problem with returns has

been introduced. The problem considered here is a

multi-item, multi-stage lot sizing problem where se-

tups are assumed negligible or included in the pro-

cessing times (similar assumptions with no returns

are made in (Chen and Ji, 2007) or in (Tonelli et al.,

2013)). On the other hand, this problem can be also

considered as a ﬂexible assembly scheduling problem

with component availability constraints (Kolisch and

Hess, 2000), where in general more than a single ma-

chine can be used to perform an operation. In ad-

dition, as the planning decisions that must be taken

include also the quantity of returned products to ac-

quire, this problem is similar to the one in (Shi et al.,

2011), where the authors aim at determining the price

for the returns considering an uncertain demand.

2 THE SYSTEM MODEL

In the considered class of production systems, manu-

facturing activities transform basic parts into ﬁnished

products through the execution of transformation or

assembly operations, and remanufacturing activities

recover basic parts from returned products and restore

them to as-new state. The system model is schema-

tized in Figure 1. The ﬁnished products are bought

and used by consumers, and, after some time, some of

them are returned for remanufacturing. The remanu-

facturing system collects returned products, if avail-

able, on the basis of its needs, and starts its reman-

ufacturing operations to recover basic parts. It is as-

sumed that each operation which recovers parts lasts

a variable amount of time, depending on the quality

of the returned product. Once recovered, the basic

parts are as new and are inserted into the inventory

of basic parts of the manufacturing system. The sys-

tem produces ﬁnished products in accordance with an

external demand to be satisﬁed.

In this work it is assumed that all the values char-

acterizing the dynamics of the system are determinis-

tic. The external demand, which varies over the time,

is known and deterministic, as well as the maximum

number of products which are returned in the various

periods of time. Moreover, it is assumed that an un-

limited number of new basic parts can be bought in

order to satisfy the production requirements. Never-

theless, the demand could be not promptly satisﬁed

due to the ﬁnite capacity of resources.

2.1 Planning of Activities

The objective of this paper is to deﬁne a mathematical

model for integrated planning of manufacturing and

remanufacturing activities. In this respect, a discrete-

time dynamics is taken into account. Let t be the

generic time bucket (or, simply, bucket) where manu-

facturing and remanufacturing operations are accom-

plished (usually, day or week, depending on the kind

of production); t = 1, ...,T, being T the planning

horizon. The planning of activities consists in deter-

mining, for each bucket, the following quantities:

• amount of components and ﬁnished products to be

manufactured,

• quantity of new basic parts to be bought,

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

752

• amount of basic parts to be recovered from re-

turned products,

• quantity of returned products to be acquired

so that a performance criterion, which basically takes

into account production, tardiness, and inventory

costs for the manufacturing part and purchasing, re-

covery, and disposal costs for the remanufacturing

part, is minimized. Such an integrated planning prob-

lem is modelled as a mixed-integer mathematical pro-

gramming problem.

2.2 Manufacturing Operations

The structure of the manufacturing operations is de-

ﬁned by the bill of materials (BOM), as the one illus-

trated in Figure 2 in which 3 types of ﬁnished prod-

ucts are carried out starting from a set of 8 kinds of

basic parts.

∆: 0

∆: 2

∆: 0

∆: 1

∆: 0

Figure 2: Bill of materials, with lead times and required

parts (example).

The following sets and values characterizing the

manufacturing system are deﬁned:

• F, C, and B are, respectively, the set of ﬁn-

ished products, the set of intermediate compo-

nents manufactured at various level of the BOM,

and the set of basic parts;

• D

p,t

is the (external) demand of product p ∈ F in

time bucket t ∈ {1,...,T};

• γ

q,p

is the quantity of parts q ∈ B∪C which are

needed to produce one unit of part p ∈ C∪ F;

• ∆

is the lead time for the production of compo-

nent or product p ∈ C∪F; ∆

= {0, 1,. ..}, where

∆

= 0 means that p is available in the same inter-

val in which the production of p starts;

• i

p,0

is the quantity of parts p ∈ B ∪ C ∪ F in the

inventory at the beginning (initial inventory level).

The manufacturing operations are carried out by

machines or production lines with eligibility con-

straints, i.e., a part (both intermediate components

and ﬁnished products) can be produced by using one

of a set of compatible machines. Then, the following

sets, parameters and variables are deﬁned:

• M is the set of machines (or production lines);

• M

is the set of machines compatible with the

production of component or product p ∈ C ∪ F;

⊆ M;

• P

is the set of components and products that can

be produced on machine m ∈ M; P

⊆ C∪F;

• Φ

m,t

is the total production capacity of machine

m ∈ M

in time bucket t ∈ {1,. .. ,T}.

The unitary costs to produce components and

products, to store parts, and to buy new basic parts

are the following:

• u

p,m,t

is the cost to produce a unit of product

p ∈ C ∪ F on machine m ∈ M

in time bucket

t ∈ {1,. .. ,T};

• u

p,h,t

is the cost due to a late production of a unit

of product p ∈ F, when it is due at time bucket

t ∈ { 1,. .. ,T} but it is produced in time bucket

h ∈ {t + 1,.. .,T + 1}; in the proposed model it is

assumed:

p,h,t

= u

· (h−t)

(1)

where

– u

is the cost paid when a unit of product p ∈ F

which is required in a certain bucket is pro-

duced in the subsequent bucket (it is the unitary

tardiness cost);

– β is a given parameter;

• u

is the cost for not producing a unit of product

p ∈ F in the planning horizon;

• u

p,t

is the inventory cost which is paid for storing

a unit of part p ∈ B ∪ C ∪ F in time bucket t ∈

{1,...,T};

• u

p,t

is the cost for acquiring a unit of new basic

part p ∈ B in time bucket t ∈ {1,...,T}.

Finally, the variables which characterize the man-

ufacturing system are the following:

• x

p,m,t

(integer variable) is the quantity of compo-

nents or products p ∈ C∪ F produced on m ∈ M

in the interval from time bucket t ∈ {1,. .. ,T} to

bucket t + ∆

(i.e., the quantity of components or

products available at the end of bucket t + ∆

);

AMixed-IntegerMathematicalProgrammingModelforIntegratedPlanningofManufacturingandRemanufacturing

Activities

753

• z

p,t

(integer variable) is the quantity of ﬁn-

ished products p ∈ F produced before bucket

t ∈ {1,. .. ,T} (thus available in the inventory) or

completed in t used for (partially) satisfy the de-

mand of p in bucket t;

• l

p,h,t

(integer variable) is the quantity of products

p ∈ F which are produced in a bucket h ∈ {t +

1,. .. ,T +1} (subsequent to buckett ∈ {1,...,T})

and used to (partially) satisfy the demand of p

in bucket t (backorder); the demand produced in

bucket T +1 corresponds to not satisﬁed demand;

• a

p,t

(integer variable) is the quantity of new basic

parts p ∈ B acquired in time bucket t ∈ {1,. ..,T};

• i

p,t

(integer variable) is the quantity of parts p ∈

B ∪ C ∪ F in the inventory at the end of bucket

t ∈ {1,. ..,T}.

2.3 Remanufacturing Operations

The remanufacturing operations are deﬁned by speci-

fying, for each of the products that can be returned,

the list of basic parts that can be retrieved. Thus,

in this work, an inverse BOM is not deﬁned for the

remanufacturing system. A remanufacturing process

for the system characterized by the BOM in Figure 2

can be that illustrated in Figure 3 in which the re-

turned products of type 1 and 2 are disassembled to

provide basic parts of type 11, 16, 19, 20, and 21.

Figure 3: Remanufacturing process, with retrieved quanti-

ties (example).

The duration of a remanufacturing operation is

a function of the quality of the returned product.

The quality is deﬁned through an integer level v ∈

{1,...,V}, being V the number of different quality

levels that are considered. The best (respectively, the

worst) quality corresponds to level 1 (resp., V). The

quality of a returned product also affects the success-

fulness of the remanufacturing activities: it is here

assumed that the worst is the quality level of the re-

turned product, the higher is the probability of ob-

taining basic parts that cannot be restored to as-new

state (in the current deterministic model, this aspect

is modelled through given percentages of parts that

can be recovered).

The following sets and values characterizing the

remanufacturing system are deﬁned:

• R is set of ﬁnished products that can be returned;

R ⊆ F;

• R

is the set of returnable ﬁnished products from

which the basic part p ∈ B can be recovered; c ∈

IC, R

⊆ R

• B

is the set of basic parts that can be obtained by

product r ∈ R through a remanufacturing process;

⊆ B;

• B

is the set of initial components that can be ob-

tained through a remanufacturing process; B

{p ∈ B : ∃r ∈ R : p ∈ B

};

• G

r,p

is the maximum amount of ﬁnished products

r ∈ R with quality v ∈ {1,...,V} that are returned

in time bucket t ∈ {1,. .. ,T};

• δ

r,p

is the quantity of basic part p ∈ B

that can be

recovered from one unit of product r ∈ R;

• ρ

r,p

is the percentage of component p ∈ B

that

can be recovered “as new” from a returned prod-

uct of family r ∈ R with quality v ∈ {1,. .. ,V};

• Γ

r,p

is the lead time for recovering basic part

p ∈ B

from ﬁnished product r ∈ R with quality

v ∈ {1, .. .,V}; Γ

r,p

= {0,1,. ..}, where Γ

r,p

= 0

means that p is available in the same interval in

which the remanufacturing process recovering p

from r starts.

• i

R,v

r,0

is the quantity of returned products r ∈ R with

quality v ∈ {1, .. .,V} in the inventory at the be-

ginning (initial inventory level).

As regards remanufacturing activities, it is as-

sumed the presence of a single dedicated machine

(i.e., not used for manufacturing operations) charac-

terized by:

• Ψ

, the total capacity of the remanufacturing ma-

chine in time bucket t ∈ {1,...,T}.

The unitary costs to purchase returned product, to

recover basic parts, and to disposal bad parts are the

following:

• u

A,v

r,t

is the cost for acquiring a unit of product r ∈

R with quality v ∈ {1, .. .,V} in time bucket t ∈

{1,...,T};

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

754

• u

r,t

is the inventory cost which is paid for storing a

unit of product r ∈ R in time bucket t ∈ {1, .. .,T};

• u

R,v

r,p,t

is the cost for recovering a unit of basic

part p ∈ B

from a unit of returned product r ∈ R

with quality v ∈ {1, .. .,V} in time bucket t ∈

{1,...,T};

• u

D,v

r,p,t

is the cost for recovering and disposal parts

for a unit of basic part p ∈ B

from a unit of re-

turned product r ∈ R with quality v ∈ {1,...,V}

in time bucket t ∈ {1,. .. ,T};

Finally, the variables which characterize the re-

manufacturing system are the following:

• a

p,t

(integer variable) is the quantity of recovered

basic parts p ∈ B

∀r ∈ R that become available in

time bucket t ∈ {1,..., T};

• a

A,v

r,t

(integer variable) is the quantity of returned

products r ∈ R with quality v ∈ {1,. .. ,V} ac-

quired in time bucket t ∈ {1,...,T} ;

• s

r,t

(integer variable) is the quantity of returned

products r ∈ R with quality v ∈ {1,. .. ,V} that

start the remanufacturing process in time bucket

t ∈ {1,. ..,T};

• i

R,v

r,t

(integer variable) is the quantity of returned

products r ∈ R with quality v ∈ {1, .. .,V} in the

inventory at the end of bucket t ∈ {1,...,T}.

3 THE MATHEMATICAL MODEL

The integrated planning of manufacturing and reman-

ufacturing activities is modelled as a mixed-integer

mathematical programming (MIP) problem and it is

solved through standard methodologies. In the fol-

lowing, the objective function to be minimized and

the constraints of the problem are reported.

3.1 The Mathematical Programming

Problem

Let w

, w

, and w

be the

weights for the objective function components.

3.1.1 Objective Function

min w

+ w

(2)

being

• total cost of production:

∑

p∈C∪F

∑

m∈M

∑

t=1

p,m,t

(3)

• total cost for late satisfaction of demand:

∑

p∈F

∑

t=1

∑

h=t+1

p,h,t

∑

p∈F

∑

t=1

∑

h=t+1

(h− t)

p,h,t

(4)

• total cost for demand not satisﬁed within the plan-

ning period:

∑

p∈F

∑

t=1

p,T+1,t

(5)

• total inventory cost:

∑

t=1



∑

p∈B∪C∪F

p,t

∑

r∈R

r,t

∑

v=1

R,v

r,t



(6)

• total cost for the acquisition of new parts:

∑

p∈B

∑

t=1

p,t

(7)

• total cost for purchasing returned products:

∑

r∈R

∑

t=1

∑

v=1

A,v

r,t

A,v

r,t

(8)

• total cost for recovery parts from returned prod-

ucts:

∑

r∈R

∑

t=1

∑

v=1



∑

p∈B

R,v

r,p,t

r,p



r,t

(9)

• total disposal cost for returned products that can-

not be recovered:

∑

r∈R

∑

t=1

∑

v=1



∑

p∈B

D,v

r,p,t

(1− ρ

r,p

) δ

r,p



r,t

(10)

3.1.2 Dynamics of Inventories

• ∀ p ∈ F : ∆

> 0, ∀t = 1,.. . ,∆

p,t−1

= z

p,t

t−1

∑

h=1

p,t,h

+ i

p,t

(11)

• ∀ p ∈ F, ∀t = ∆

+ 1,. .. ,T:

∑

m∈M

p,m,t−∆

+ i

p,t−1

= z

p,t

t−1

∑

h=1

p,t,h

+ i

p,t

(12)

AMixed-IntegerMathematicalProgrammingModelforIntegratedPlanningofManufacturingandRemanufacturing

Activities

755

• ∀ p ∈ F, ∀t = 1, .. . ,T:

p,t

T+1

∑

h=t+1

p,h,t

= D

p,t

(13)

• ∀ p ∈ C : ∆

> 0, ∀t = 1,.. ., ∆

p,t−1

∑

q∈C∪F

∑

m∈M

p,q

q,m,t

+ i

p,t

(14)

• ∀ p ∈ C, ∀t = ∆

+ 1,. ..,T:

∑

m∈M

p,m,t−∆

p,t−1

∑

q∈C∪F

∑

m∈M

p,q

q,m,t

p,t

(15)

• ∀ p ∈ B, ∀t = 1,...,T:

p,t−1

+ a

p,t

+ a

p,t

∑

q∈C∪F

∑

m∈M

p,q

q,m,t

+ i

p,t

(16)

• ∀ p ∈ B

, ∀t = 1,...,T:

p,t

∑

r∈R: p∈B



∑

v=1

r,p

r,t−Γ

r,p



(17)

• ∀ p ∈ B, p /∈ B

, ∀t = 1,...,T:

p,t

= 0 (18)

• ∀ r ∈ R, ∀t = 1,...,T, ∀ v = 1,... ,V:

R,v

r,t−1

+ a

A,v

r,t

= s

r,t

+ i

R,v

r,t

(19)

• ∀ r ∈ R, ∀t = 1,...,T, ∀ v = 1,... ,V:

A,v

r,t

≤ G

r,t

(20)

3.1.3 Capacity constraints

• ∀ m ∈ M, ∀t = 1,. .. ,T:

∑

p∈P

∆

∑

h=0

p,m,t−h

≤ Φ

m,t

(21)

• ∀t = 1,...,T:

∑

r∈R

∑

p∈B



∑

v=1

r,p

∑

h=1

r,p

r,t−h



≤ Ψ

(22)

This problem, in which all the involved quantities

are restricted to integer values, is NP-hard as it gener-

alizes the deterministic capacitated planning problem

with no setup costs which is NP-hard itself, as proved

in (Florian et al., 1980).

4 EXAMPLE

The MIP problem described in the previous section

has been implemented in a C# procedure and solved

by the Cplex 12.5 MIP solver. To test the correct-

ness of the proposed approach, an example which is

reported in the following has been deﬁned.

Consider an integrated manufacturing-

remanufacturing system, whose bill of materials

and remanufacturing process are those reported in

Figures 2 and 3, respectively. The system produces

three types of ﬁnished products. Two out of three

types of products can be returned (1 and 2) and the

remanufacturing process can provide ﬁve out of eight

types of basic parts (11, 16, 19, 20, and 21; part 16

can be recovered from both products of type 1 and

products of type 2). Four machines are in the system:

machine 1 can produce parts (ﬁnished products

and intermediate component) 3, 4, 6, 8, 9, 12, 15;

machine 2 can produce parts 6, 8, 9, 12, 15; machine

3 can produce parts 1, 2, 5, 7; machine 4 can produce

parts 5, 7, 10, 14; the capacity of each machine

varies with time, in the range [200,400] parts/day.

A ﬁfth machine, whose capacity is 100 parts/day,

is dedicated to the remanufacturing activities. The

system must satisfy an external demand over a period

of T = 12 days; the values of such a demand are

reported in Table 1. All inventories are null at the

beginning, even those in which acquired returned

products are stored before they are disassembled.

Table 1: Example – Demand of products.

t → 1 2 3 4 5 6

1,t

21 26 31 33 28 37

2,t

27 21 16 19 17 19

3,t

25 30 18 25 19 25

t → 7 8 9 10 11 12

1,t

35 40 31 26 22 32

2,t

22 23 22 29 23 30

3,t

26 16 19 18 25 28

It is assumed that the quality of the returned prod-

ucts can be discretized in 3 levels (V = 3), being 1 the

better level and 3 the worst one. The lead times for

recovering components are 1, 1, and 2 (respectively

for quality 1, 2, and 3) for products of type 1, and 0,

1, and 1 for products of type 2. Moreover, the per-

centage of components that can be retrieved “as new”

is set to 0.8, 0.6, and 0.4 for products of type 1, and

to 1, 0.75, and 0.5 for products of type 2. The number

of returned products that can be acquired varies with

time and with the quality level; it is here assumed that

all such numbers range in the interval [5,30].

The unitary costs are not reported here due to the

lack of space; it is only mentioned that the cost for

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

756

not producing a (demanded) unit of product is signif-

icantly larger than the other unitary costs, in order to

discourage the non-fulﬁlment of the external demand.

Besides, in the last part of the example, an analysis

of the sensitiveness of the solution with respect of the

unitary costs will be carried out. Finally, all weights

for the objective function components are unitary.

4.1 Solution of the Problem

The instance of the problem brieﬂy described in the

previous section has been solved by the Cplex 12.5

MIP solver. During the experimentalanalysis the MIP

model was solved with a 120 seconds time limit, gen-

erating solutions with a 0.3-0.4% of optimality gap on

a standard laptop with Intel’s Core i7 processor and 8

Gb RAM.

Tables 2-7 report an example of the obtained so-

lutions, showing in particular the values for the deci-

sion variables x

p,m,t

and a

p,t

(relevant to the manufac-

turing operations) and a

A,v

r,t

, s

r,t

, and a

p,t

(relevant to

the remanufacturing process). In all solutions the de-

mand for the products was satisﬁed within the plan-

ning horizon with a quite limited tardiness: in partic-

ular, the initial demands for products 1 and 3 were

not satisﬁed on time due to the lead times involved

in their production processes, having assumed no ini-

tial inventory for basic parts and intermediate compo-

nents; in addition, only 7 units of product 3 due on

bucket 5 and 1 unit of product 2 due on bucket 9 were

delivered with tardiness.

4.2 Sensitivity of the Solution

A ﬁrst analysis of the sensitiveness of the solution

with respect of the unitary costs has been carried

out. The solution of the problem has been deter-

mined as a function of the rates µ

/ν

, ∀p ∈ B

, be-

ing µ

= µ

p,t

) and ν

= ν

A,v

r,t

R,v

r,p,t

D,v

r,p,t

)

two values adopted to estimate the cost to buy and the

cost to recover, respectively, a unit of a basic part of

type p. The quantities µ

and ν

are computed as:

∑

t=1

p,t

(23)

∑

r∈R



∑

r,p



∑

v=1

∑

t=1

A,v

r,t

∑

t=1

r,t



∑

v=1

∑

t=1

r,p

R,v

r,p,t

∑

v=1

∑

t=1



1− ρ

r,p



D,v

r,p,t



(24)

0.1 0.4 0.5 0.6 0.7 0.8 1.5

200

400

600

800

1000

Basic part type 11

0.1 0.4 0.5 0.6 0.7 0.8 1.5

200

400

600

800

1000

Basic part type 16

0.1 0.4 0.5 0.6 0.7 0.8 1.5

200

400

600

800

1000

Basic part type 19

0.1 0.4 0.5 0.6 0.7 0.8 1.5

200

400

600

800

1000

Basic part type 20

0.1 0.4 0.5 0.6 0.7 0.8 1.5

200

400

600

800

1000

Basic part type 21

Figure 4: Overall number of basic parts acquired new

(straight line) and recovered (dash line) as function of the

rate µ

/ν

ranging from 0.1 to 1.5.

The analysis has been carried out by considering

a ﬁxed ν

and a variable µ

. In particular, for any

p ∈ B

, µ

has been set in accordance with ν

in or-

der to obtain, for the rate µ

/ν

, the values in the in-

terval [0.1,1.5], with step size 0.025 from 0.4 to 0.8

and step size 0.1 elsewhere in the interval. The results

of such analysis are in Figure 4, which shows patterns

that are coherent with the considered class of system.

Besides, such a ﬁrst analysis can be considered as

a basic validation of the integration of manufactur-

ing and remanufacturing activities. In this connec-

tion, unlimited capacity of the resources (both of the

AMixed-IntegerMathematicalProgrammingModelforIntegratedPlanningofManufacturingandRemanufacturing

Activities

757

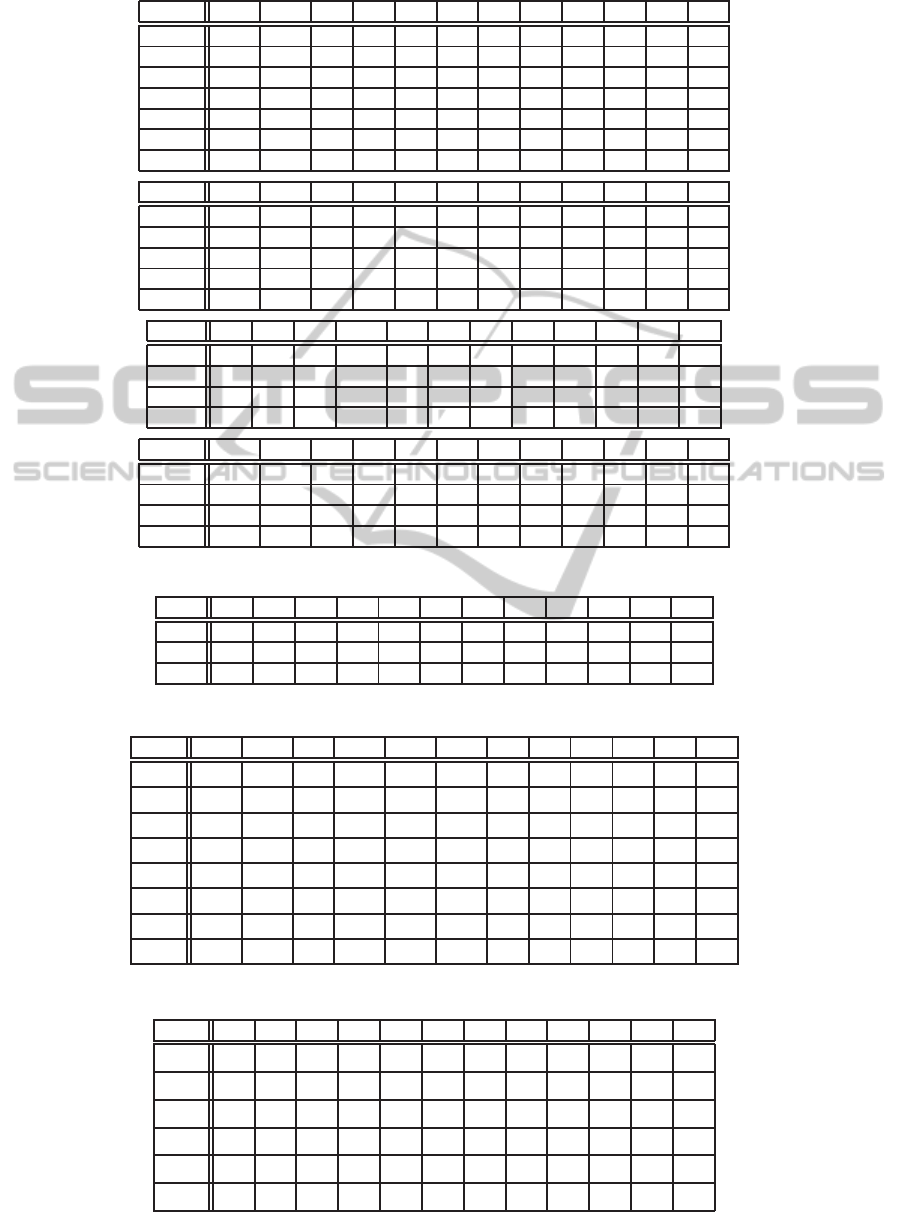
Table 2: Example – Solution variable x

p,m,t

(production plan on the four machines).

t → 1 2 3 4 5 6 7 8 9 10 11 12

3,1,t

73 25 12 32 42 0 19 18 25 28 0 0

4,1,t

0 111 28 37 35 40 31 26 25 29 0 0

6,1,t

100 46 28 51 59 19 43 41 44 58 43 10

8,1,t

0 0 0 35 0 0 0 0 0 0 0 0

9,1,t

0 0 0 37 0 40 0 26 0 29 0 0

12,1,t

73 25 12 0 0 0 19 18 0 28 0 0

15,1,t

0 222 56 0 70 0 62 0 0 0 0 0

t → 1 2 3 4 5 6 7 8 9 10 11 12

6,2,t

0 0 0 0 0 0 0 0 0 0 0 0

8,2,t

111 49 16 0 40 53 4 25 29 0 0 0

9,2,t

0 111 28 0 35 0 31 0 25 0 0 0

12,2,t

0 0 0 32 42 0 0 0 25 0 0 0

15,2,t

0 0 0 74 0 80 0 52 50 58 0 0

t → 1 2 3 4 5 6 7 8 9 10 11 12

1,3,t

0 0 0 111 28 37 35 40 31 26 25 29

2,3,t

27 21 16 19 17 19 22 23 21 30 23 30

5,3,t

27 21 0 0 0 0 0 23 0 30 23 30

7,3,t

73 25 0 32 42 0 19 18 0 28 0 0

t → 1 2 3 4 5 6 7 8 9 10 11 12

5,4,t

0 0 16 19 17 19 22 0 21 0 0 0

7,4,t

0 0 12 0 0 0 0 0 25 0 0 0

10,4,t

100 157 56 88 94 59 74 67 69 87 43 10

14,4,t

111 49 16 35 40 53 4 25 29 0 0 0

Table 3: Example – Solution variable z

p,t

(demand satisﬁed on time).

t → 1 2 3 4 5 6 7 8 9 10 11 12

1,t

0 0 0 33 28 37 35 40 31 26 22 32

2,t

27 21 16 19 17 19 22 23 21 29 23 30

3,t

0 0 18 25 12 25 26 16 19 18 25 28

Table 4: Example – Solution variable a

p,t

(acquisition plan of new basic parts).

t → 1 2 3 4 5 6 7 8 9 10 11 12

11,t

68 6 0 0 0 0 0 0 0 0 0 0

13,t

333 147 48 105 120 171 0 75 87 0 0 0

16,t

68 68 0 21 40 9 26 10 0 23 0 0

17,t

146 50 24 64 84 0 38 36 50 56 0 0

18,t

146 50 24 64 84 0 38 36 50 56 0 0

19,t

111 0 0 19 33 30 0 0 4 0 0 0

20,t

0 124 0 66 56 34 36 20 0 46 0 0

21,t

0 124 0 66 56 34 36 20 0 46 0 0

Table 5: Example – Solution variable a

A,v

r,t

(acquisition plan of returned products for remanufacturing).

t → 1 2 3 4 5 6 7 8 9 10 11 12

A,1

1,t

0 0 0 0 0 2 0 0 0 0 0 0

A,2

1,t

22 0 0 5 15 3 8 12 0 0 0 0

A,3

1,t

13 10 0 0 0 0 2 3 0 0 0 0

A,1

2,t

15 3 15 15 6 15 10 0 0 0 0 0

A,2

2,t

7 0 1 0 0 0 0 0 4 13 8 0

A,3

2,t

10 1 10 11 7 6 1 15 20 15 0 0

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

758

Table 6: Example – Solution variable s

r,t

(remanufacturing process).

t → 1 2 3 4 5 6 7 8 9 10 11 12

1,t

0 0 0 0 0 2 0 0 0 0 0 0

1,t

22 0 0 5 15 3 8 12 0 0 0 0

1,t

13 10 0 0 0 0 2 3 0 0 0 0

2,t

15 0 16 17 5 6 20 0 0 0 0 0

2,t

7 0 1 0 0 0 0 0 4 13 8 0

2,t

10 0 11 11 7 6 0 16 20 15 0 0

Table 7: Example – Solution variable a

p,t

(basic parts recovered in the remanufacturing process).

t → 1 2 3 4 5 6 7 8 9 10 11 12

11,t

32 40 28 63 47 27 35 41 44 58 43 10

16,t

32 89 56 67 54 50 48 57 69 64 43 10

19,t

0 49 28 4 7 23 13 16 25 6 0 0

20,t

0 98 56 8 14 46 26 32 50 12 0 0

21,t

0 98 56 8 14 46 26 32 50 12 0 0

manufacturing part and of the remanufacturing one)

and unlimited availability of returned products have

been assumed in this analysis, in order to make the

sensitiveness independent from the availability of ma-

chines and of products to be disassembled in order to

recover basic parts.

5 CONCLUSIONS

This work proposes a MIP model for planning man-

ufacturing activities in a multi-product, multi-stage

production plant which includes a remanufacturing

facility. The considered model assumes a simpliﬁed

aggregate production characterized by deterministic

information on demand and availability of returned

products. The presented experimental analysis points

out the applicability of the model at least for small-

medium size instances (the problem in the consid-

ered example has about 1150 variables and 560 con-

straints), as well as the coherence of the model be-

haviour with respect to the variations of part acquisi-

tion costs. In any case, more extensive testing with

larger instances is on its way. Besides, future im-

provements of this model will focus on the consider-

ation of explicit setups and on the relaxation of some

of the deterministic assumptions.

REFERENCES

Chen, K. and Ji, P. (2007). A mixed integer program-

ming model for advanced planning and scheduling

(aps). European Journal of Operational Research,

181(1):515–522.

Fleischmann, M., Bloemhof-Ruwaard, J. M., Dekker, R.,

van der Laan, E., van Nunen, J. A., and Van Wassen-

hove, L. N. (1997). Quantitative models for reverse

logistics: A review. European Journal of Operational

Rcsearch, 103:1–17.

Florian, M., Lenstra, J., and Rinnooy Kan, A. (1980). De-

terministic production planning: Algorithms and com-

plexity. Management Science, 26(7):669–679.

Guide Jr., V. D. R. (2000). Production planning and control

for remanufacturing: industry practice and research

needs. Journal of Operations Management, 18:467–

483.

Guide Jr., V. D. R. and Van Wassenhove, L. N. (2009). The

evolution of closed-loop supply chain research. Oper-

ations Research, 57(1):10–18.

Kolisch, R. and Hess, K. (2000). Efﬁcient methods for

scheduling make-to-order assemblies under resource,

assembly area and part availability constraints. Inter-

national Journal of Production Research, 38(1):207–

228.

Lund, R. T. (1985). Remanufacturing: The experienceof the

united states and implications for developing coun-

tries. World Bank Technical Paper 31, The World

Bank.

Shi, J., Zhang, G., and Sha, J. (2011). Optimal production

planning for a multi-product closed loop system with

uncertain demand and return. Computers & Opera-

tions Research, 38:641–650.

Teunter, R. H., Bayindir, Z. P., and Van Den Heuvel, W.

(2006). Dynamic lot sizing with product returns and

remanufacturing dynamic lot sizing with product re-

turns and remanufacturing dynamic lot sizing with

product returns and remanufacturing. International

Journal of Production Research, 44(20):4377–4400.

Thierry, M., Salomon, M., Van Nunen, J., and Van Wassen-

hove, L. N. (1995). Strategic issues in product re-

covery management. California Management Review,

37(2):114–135.

Tonelli, F., Paolucci, M., Anghinolﬁ, D., and Taticchi, P.

(2013). Production planning of mixed-model assem-

bly lines: A heuristic mixed integer programming

based approach. Production Planning and Control,

24(1):110–127.

Zhang, H., Li, J., Shrivastava, P., Whitley, A., and Mer-

chant, M. E. (2004). A web-based system for reverse

manufacturing and product environmental impact as-

sessment considering end-of-life dispositions. CIRP

Annals - Manufacturing Technology, 53(1):5–8.

AMixed-IntegerMathematicalProgrammingModelforIntegratedPlanningofManufacturingandRemanufacturing

Activities

759