Image Denoising Algorithm with a Three-dimensional Grid System of

Coupled Nonlinear Elements

Atsushi Nomura

, Yoshiki Mizukami

and Koichi Okada

Faculty of Education, Yamaguchi University, Yoshida 1677-1, Yamaguchi 753-8513, Japan

Graduate School of Science and Engineering, Yamaguchi University, Tokiwadai 2-16-1, Ube 755-8611, Japan

Center for the Promotion of Higher Education, Yamaguchi University, Yoshida 1677-1, Yamaguchi 753-8511, Japan

Keywords:

FitzHugh-Nagumo, Coupled Nonlinear Elements, Three-dimensional Grid, Reaction-diffusion, ODE.

Abstract:

This paper presents an image denoising algorithm with a three-dimensional grid system of coupled nonlinear

elements. The system consists of a two-dimensional image grid and a one-dimensional grid representing a

quantized image brightness. At each grid point, a FitzHugh-Nagumo type nonlinear element is placed and

coupled with other elements placed at its nearest neighboring grid points. The FitzHugh-Nagumo element is

described with a set of time-evolving ordinary differential equations, and is tuned to be excitable. When we

externally stimulate the grid system with an image brightness distribution, we could observe that noise in the

distribution was reduced and signal was strengthened as time proceeds. Thus, the image denoising algorithm

utilizes this property of the grid system, in which we propose to modify external stimuli so as to have broad

Gaussian distributions. We conﬁrm performance of the algorithm on artiﬁcial and real images in comparison

with two classical algorithms of a diffusion equation and median ﬁltering.

1 INTRODUCTION

Gaussian ﬁltering is a classical and elementary tech-

nique for smoothing and denoising in image pro-

cessing and computer vision (Gonzalez and Woods,

1992). We convolve a Gaussian function with an

image brightness distribution, and obtain its blurred

or smoothed distribution. A diffusion equation gives

the mathematically equal result with Gaussian ﬁlter-

ing (Koenderink, 1984). This is because a solution of

the diffusion equation is expressed by a convolution

of a Gaussian function with its initial condition.

There is a trade-off between reducing image noise

and preserving image structures. If we try to reduce

noise with a Gaussian function having a large spatial

spread, we shall obtain much smoothed or fully de-

noised image. However, at the same time Gaussian

ﬁltering removesdetailed structures of the image such

as edges and feature points. Thus, image denoising

algorithms are required to reduce noise as well as to

preserve detailed image structures.

Perona and Malik proposed an image processing

algorithm utilizing a diffusion equation, in which its

diffusion coefﬁcient is anisotropic and is modulated

according to a gradient of an image brightness distri-

bution (Perona and Malik, 1990; Mr´azek and Navara,

2003). They intended to prevent over-smoothing

across image edges. Tomasi and Manduchi proposed

an extension of Gaussian ﬁltering, named ‘bilateral

ﬁltering’ (Tomasi and Manduchi, 1998), which in-

cludes geometric closeness and photometric similar-

ity as the kernel of Gaussian ﬁltering; the classical

Gaussian ﬁltering relies on only the geometric close-

ness. A nonlocal means algorithm (Buades et al.,

2010) is another extension of Gaussian ﬁltering; the

novel point of the algorithm is to utilize windows hav-

ing brightness patterns similar to that of a target win-

dow.

There are several image denoising approaches

such as median ﬁltering (Gonzalez and Woods, 1992;

Eng and Ma, 2001), a total variation approach (Guo

et al., 2011) and a nonlocal approach (Buades et al.,

2010; Dabov et al., 2007; Katkovnik et al., 2010).

The median ﬁltering constructs a histogram on im-

age brightness in a local area, and chooses a mid-

dle brightness level as its representative. The total

variation approach deﬁnes a functional taking account

of noise property, derives a Euler-Lagrange type

reaction-diffusion equation, and numerically solves

the equation. The nonlocal approach was devel-

opped from the idea of the nonlocal means algo-

rithm (Buades et al., 2010); see also the review ar-

220

Nomura A., Mizukami Y. and Okada K..

Image Denoising Algorithm with a Three-dimensional Grid System of Coupled Nonlinear Elements.

DOI: 10.5220/0005119302200225

In Proceedings of the 11th International Conference on Signal Processing and Multimedia Applications (SIGMAP-2014), pages 220-225

ISBN: 978-989-758-046-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

ticles (Buades et al., 2010; Katkovnik et al., 2010).

Nomura et al. (2012) proposed a stereo algo-

rithm with a three-dimensional grid system of cou-

pled nonlinear elements. The algorithm success-

fully reconstructs a disparity distribution in the three-

dimensional grid system of the elements externally

stimulated by a similarity measure between stereo

images. In the algorithm, they placed a FitzHugh-

Nagumo type nonlinear excitable element at each

grid point, and coupled neighboring elements. The

three-dimensional grid system approximates to a

three-dimensional FitzHugh-Nagumo type reaction-

diffusion system (FitzHugh, 1961; Nagumo et al.,

1962); a one-dimensional version of the system de-

scribes a pulse propagation phenomenon along nerve

axon, and has a biological background.

Inspired by the previous stereo algorithm (No-

mura et al., 2012) having the biological background,

we propose an image denoising algorithm with the

isotropic three-dimensional grid system of coupled

FitzHugh-Nagumo nonlinear excitable elements. The

novel point of the proposed algorithm lies in the man-

ner of externally stimulating the elements in compar-

ison with the previous stereo algorithm. We apply

the algorithm and two other classical ones to artiﬁ-

cial and real images, and conﬁrm their quantitative

performance.

2 THE ALGORITHM

2.1 FitzHugh-Nagumo Element

A FitzHugh-Nagumo element is described with a set

of equations having two variables of an activator u(t)

and an inhibitor v(t) (FitzHugh, 1961; Nagumo et al.,

1962), as follows:

= f(u,v) + µS =

[u(u− a)(1− u) − v] + µS,

(1)

= g(u,v) = u− bv, (2)

in which a and b are constants controlling the stability

characteristic of the element, and ε is a small constant

(0 < ε ≪ 1); S is an external stimulus and µ is its

coefﬁcient. Depending on the parameter settings of

a,b and ε under µS = 0, the element becomes mono-

stable or bi-stable, as shown in Fig. 1. For example,

the element becomes bi-stable in the case of a = 0.3

and b = 10; any solution (u, v) converges to either of

the stable points A or B. An excited state refers to the

area having u ≃ 1 around B, and a resting state refers

to the area having u ≃ 0 around A. We can roughly

-0.10

-0.05

0.00

0.05

0.10

0.15

-0.2 0.0 0.2 0.4 0.6 0.8 1.0 1.2

a=0.2 a=0.3 a=0.4

B’

Excited state

Resting state

f(u,v)=0

g(u,v)=0

Figure 1: Null-clines of f (u,v) = g(u,v) = 0 in a FitzHugh-

Nagumo type nonlinear element of Eqs. (1) and (2) with a =

0.2,0.3,0.4, the ﬁxed b = 10 and µS = 0. The element has

stable steady states denoted by A, B and B’, depending on

the parameter settings; it becomes bi-stable in the cases of

a = 0.2,0.3, and mono-stable in that of a = 0.4. An excited

state refers to the area having u ≃ 1 around B and B’, and a

resting state refers to the area having u ≃ 0 around A.

explain that the parameter a in Eq. (1) is a threshold

level for dividing a state of an element into either of

an excited state or a resting state under the constraint

of v = 0.

2.2 Coupled Elements in a

Three-dimensional Grid

Let I

i, j

be image brightness observed at a point (i, j)

on an image grid X × Y. The image brightness is

quantized into (N + 1) gray levels Z = {0,1,··· ,N}.

Images should satisfy two constraints: uniqueness

and continuity. The uniqueness constraint requires

that a particular image point (i, j) has only one bright-

ness level I

i, j

. The continuity constraint assumes that

neighboring points have the same or similar bright-

ness levels except for boundaries of brightness pat-

terns. These constraints are similar to those of the

stereo vision problem (Nomura et al., 2012). Ran-

domly distributing noise does not satisfy the continu-

ity constraint; an algorithm with the two constraints is

expected to reduce random noise.

A three-dimensional grid system utilized here

consists of (i, j,k) ∈ X × Y × Z, in which coupled

FitzHugh-Nagumo type nonlinear elements having

i, j,k

) are placed at the grid points according to

the manner of Nomura et al. (2012), as follows:

i, j,k

= C

i, j,k

− 6u

i, j,k

+ f(u

i, j,k

) + µS

i, j,k

, (3)

i, j,k

= C

i, j,k

− 6v

i, j,k

+ g(u

i, j,k

), (4)

ImageDenoisingAlgorithmwithaThree-dimensionalGridSystemofCoupledNonlinearElements

221

in which

i, j,k

∑

′

, j

′

)∈ℓ

i+i

′

, j+ j

′

,k+k

′

with

ℓ={(−1,0,0),(1,0,0),(0,−1,0),(0,1,0),(0,0,−1),(0,0,1)}.

Note that the neighboring elements are coupled via

both of the activator and inhibitor variables.

A system of the coupled elements has a property

in which an excited state propagates into its neighbor-

ing areas. Thus, we can expect that an area stimulated

by positive µS

i, j,k

becomes an excited state and ex-

tends into its neighboring areas over noise; this prop-

erty works for the continuity constraint. For image

denoising, the system needs to satisfy the unique-

ness constraint, which allows each grid point (i, j) to

have only one brightness level. If a grid point (i, j, k)

has already reached an excited state, the other grid

points (i, j,k

′

), k

′

∈ Z \ {k}, at the same image grid

point (i, j) must be inhibited to reach excited states;

Z \ {k} denotes a set of grid points excluding the

point k in Z. Let us recall that the parameter a in

Eq. (1) is the threshold level which divides a state

of an element into an excited state or a resting state.

Thus, we do not ﬁx the parameter a, but modulate

the parameter depending on states of other grid points

(i, j,k

′

), k

′

∈ Z\ {k}, as follows:

i, j,k

= A

− A



1+ tanh



max

′

∈Z\{k}

i, j,k

′

− A



, (5)

in which A

and A

are constants and Eq. (5) is

monotonically increasing.

A system of diffusively coupled FitzHugh-

Nagumo elements, that is, a set of FitzHugh-Nagumo

type reaction-diffusion equations simulates a pulse

propagation phenomenon observed along a nerve

axon (FitzHugh, 1961; Nagumo et al., 1962); the

pulse propagation is stable, even if there is a little

noise on the nerve axon. Thus, a set of Eqs. (3) and (4)

with a ﬁxed a

i, j,k

= a and the ﬁrst order neighborhood

ℓ roughly approximates to the FitzHugh-Nagumo type

reaction-diffusion equations, and has the biological

background of the pulse propagation.

In addition, by imposing the condition of

f(u

i, j,k

) = g(u

i, j,k

) = S

i, j,k

= 0 on Eqs. (3)

and (4), we obtain an approximated discrete version

of two diffusion equations. An algorithm of Gaussian

ﬁltering is realized with a two-dimensional version of

either Eqs. (3) or (4) under the condition.

Temporal discretization of Eqs. (3) and (4) pro-

vides a set of linear equations. With appropriate ini-

tial conditions and boundary ones on the two variables

i,j

i+1,j

i-1,j

i+1,j

i,j

i+1,j,I

i+1,j

i,j,I

i,j

i-1,j,I

i-1,j

noise

i-1,j

i+1,j

i,j

i+1,j,I

i+1,j

i,j,I

i,j

i-1,j,I

i-1,j

noise

(a) (b)

Figure 2: External stimuli S

i, j,k

for the proposed algorithm

in a situation of a noise-perturbed image brightness distri-

bution I

i, j

; the image brightness I

i, j

is perturbed with a noise

at an image point (i, j). Figure (a) shows three external

stimuli with S

i−1, j,k

= δ(k − I

i−1, j

),S

i, j,k

= δ(k − I

i, j

) and

i+1, j,k

= δ(k−I

i+1, j

), in which δ(·) denotes the delta func-

tion. Figure (b) shows three external stimuli proposed with

Eq. (6).

i, j,k

), we can numerically compute temporal

developments of the two variables.

2.3 External Stimuli

Now, we propose a manner of externally stimulat-

ing each element in the grid system. Let us con-

sider a situation in which an image point is perturbed

with noise and its surrounding points are not. If the

delta function is employed as S

i, j,k

= δ(k − I

i, j

), the

noise prevents two adjacent image grid points with the

same brightness level from strengthening each other

through Eq. (3), as shown in Fig. 2(a). Thus, this pa-

per proposes to employ the following external stimu-

lus

i, j,k

= exp



−

(k− I

i, j

)



(6)

so as to give the stimulus more widely along the k-

direction as shown in Fig. 2(b); σ in Eq.(6) denotes

the width of the Gaussian.

Initial conditions for u

i, j,k

and v

i, j,k

are set to zero

at all points (i, j,k) ∈ X × Y × Z. A zero-gradient

boundary condition governs borders of the grid sys-

tem X× Y× Z.

After ﬁnite duration of time (0 < t ≤ L

), the algo-

rithm creates a denoised image

∗

i, j

= argmax

k∈Z

i, j,k

(7)

Algorithm 1 gives a pseudo code of the algorithm.

3 EXPERIMENTAL RESULTS

We applied three image denoising algorithms to arti-

ﬁcial and real images, and evaluated their results. The

three algorithms were as follows: the proposed algo-

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

222

(a) (b) (c) (d)PSNR=28.2 dB PSNR=20.2 dB PSNR=29.2 dB PSNR=27.7 dB

Figure 3: Experimental results of image denoising with the proposed algorithm, a diffusion algorithm and median ﬁltering on

an artiﬁcial image. Figure (a) shows the artiﬁcial image (500×500 pixels and 256 brightness levels) with an additive Gaussian

noise of the standard deviation 10 and zero-average [see Ref. (Nomura et al., 2011) for the original artiﬁcial image without

noise]. Figure (b) shows a result obtained by the proposed algorithm at t = 10 with the parameter setting of C

= 25,C

100,A

= 0.07,A

= 0.7,A

= 0.5,b = 10,ε = 1.0× 10

−2

,∆t = 1/100 and σ = 10. Figure (c) shows a result obtained by the

diffusion algorithm at t = 0.04 with the parameter setting of C

= 2.5 and ∆t = 1/100. Figure (d) shows a result obtained by

the median ﬁltering with a local area of 5× 5 pixels. Each ﬁgure has a value evaluated by the measure PSNR.

(e)

(a) (b) (c) (d)

PSNR=28.7 dB PSNR=30.5 dB PSNR=35.4 dB PSNR=35.3 dB

PSNR=28.7 dB

100

150

200

100 200 300 400 500

i,j=255

Original image

Median filter

Diffusion

Proposed

j=255

-0.3

1.0

0.0

(f)

t=0.1

i0 528

255

t=1.0

255

i0 528

t=5.0

255

i0 528

Figure 4: Experimental results of image denoising with the proposed algorithm, a diffusion algorithm and median ﬁltering

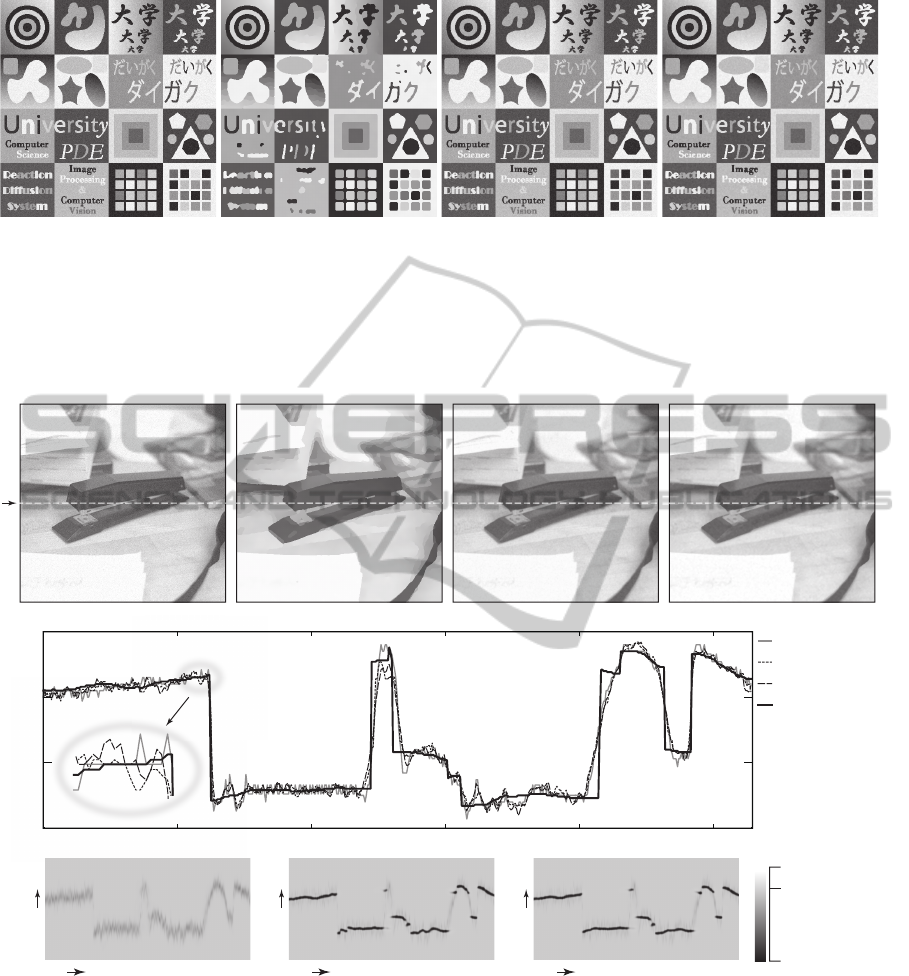
on a real image provided on a website (Heath et al., 2014). Figure (a) shows the real image (529 × 510 pixels and 256

brightness levels) with an additive Gaussian noise of the standard deviation 10 and zero-average. Figure (b) shows a result

obtained by the proposed algorithm at t = 10 with the same parameter setting as that of Fig. 3(b). Figure (c) shows a result

obtained by the diffusion algorithm at t = 0.24 with the same parameter setting as that of Fig. 3(c). Figure (d) shows a result

obtained by the median ﬁltering with a local area of 3× 3 pixels. Each of Figs. (a)∼(d) has a value evaluated by the measure

PSNR. Figure (e) shows one-dimensional proﬁles I

i, j=255

of the brightness distributions of the original image and the results

shown in Figs. (b)∼(d); the proﬁles around i = 110 are enlarged for more detailed conﬁrmation. Figure (f) shows temporal

developments of a two-dimensional distribution u

i, j=255,k

obtained at t = 0.1,1.0,5.0 by the proposed algorithm; a gray level

shows the distribution u

i, j=255,k

, and thus black areas indicate excited states of elements. The maximum value at each image

point (i, j) along the direction k is chosen, and its k value denotes the brightness level of the denoised image [see Eq. (7)].

ImageDenoisingAlgorithmwithaThree-dimensionalGridSystemofCoupledNonlinearElements

223

Algorithm 1 : Proposed image denoising algorithm, in

which Eqs. (3) and (4) are discretized with a ﬁnite time-

difference ∆t for their numerical computation.

1: for all (i, j) ∈ X× Y do

2: for all k ∈ Z do

3: S

i, j,k

← exp



−

(k−I

i, j

)



⊲ Eq.( 6)

4: u

n=0

i, j,k

← 0, v

n=0

i, j,k

← 0 ⊲ Initial conditions.

5: end for

6: end for

7: n ← 0

8: while n < L

/∆t do

9: for all (i, j,k) ∈ X× Y× Z do

10: Compute u

n+1

i, j,k

n+1

i, j,k

. ⊲ Eqs. (3)∼(5)

11: end for

12: n ← n + 1

13: end while

14: for all (i, j) ∈ X× Y do

15: I

∗

i, j

← argmax

k∈Z

i, j,k

⊲ Eq. (7)

16: end for

rithm, a diffusion algorithm and median ﬁltering. The

diffusion algorithm utilizes a simple diffusion equa-

tion with the initial condition of an image brightness

distribution. The median ﬁltering has a local area in

which the median of brightness values is chosen as the

representativebrightness value (Gonzalez and Woods,

1992).

The following peak-signal-to-noise-ratio (PSNR)

evaluates image quality, as follows:

PSNR = 10log

|X× Y|

∑

(i, j)∈X×Y

i, j

− I

i, j

)

[dB],

(8)

in which I

i, j

denotes the original image without noise,

i, j

denotes an image for quality assessment, and |X×

Y| denotes the image size.

Figure 3 shows results of image denoising on an

artiﬁcial image with an additive Gaussian noise. Ac-

cording to the measure PSNR, the diffusion algorithm

achieved the best performance of 29.2 dB, which is

better than the level of PSNR = 28.2 dB measured on

the input image, and performance of the other two al-

gorithms was worse than the level of the input image.

Figure 4 shows results of image denoising on an

image generated by adding a Gaussian noise to a

real photo image (Heath et al., 2014). According to

the measure PSNR, the two algorithms of the dif-

fusion algorithm and the median ﬁltering achieved

almost the same performance of about 35 dB, and

the proposed algorithm gave 30.5 dB which is bet-

ter than the quality of the input image 28.7 dB of

Fig. 4(a). For more detailed conﬁrmation on the re-

0.1

1.0 10

PSNR [dB]

(d)Diffusion algorithm

applied to the real image

(c)Diffusion algorithm

applied to the artificial image

(b)Proposed algorithm

applied to the real image

(a)Proposed algorithm

applied to the artificial image

0.01 0.1 1.0

(a) ,(b)

Figure 5: Image denoising processes evaluated by the mea-

sure PSNR. Curves (a) and (b) show results of the proposed

algorithm applied to the artiﬁcial and real images (see Figs 3

and 4). Curves (c) and (d) show results of the diffusion al-

gorithm applied to the same artiﬁcial and real images; the

algorithm achieved the best performance at t = 0.04 on the

artiﬁcial image, and at t = 0.24 on the real image. Note that

a time scale for (a) and (b) is different from that for (c) and

(d).

sults, Fig. 4(e) shows one-dimensional proﬁles of im-

age brightness distributions at the center (j = 255) in

the images of Figs. 4(a)∼(d). Figure 4(f) shows the

temporal developments of a two-dimensional distri-

bution u

i, j=255,k

, (i,k) ∈ X × Z obtained at three dif-

ferent time instances.

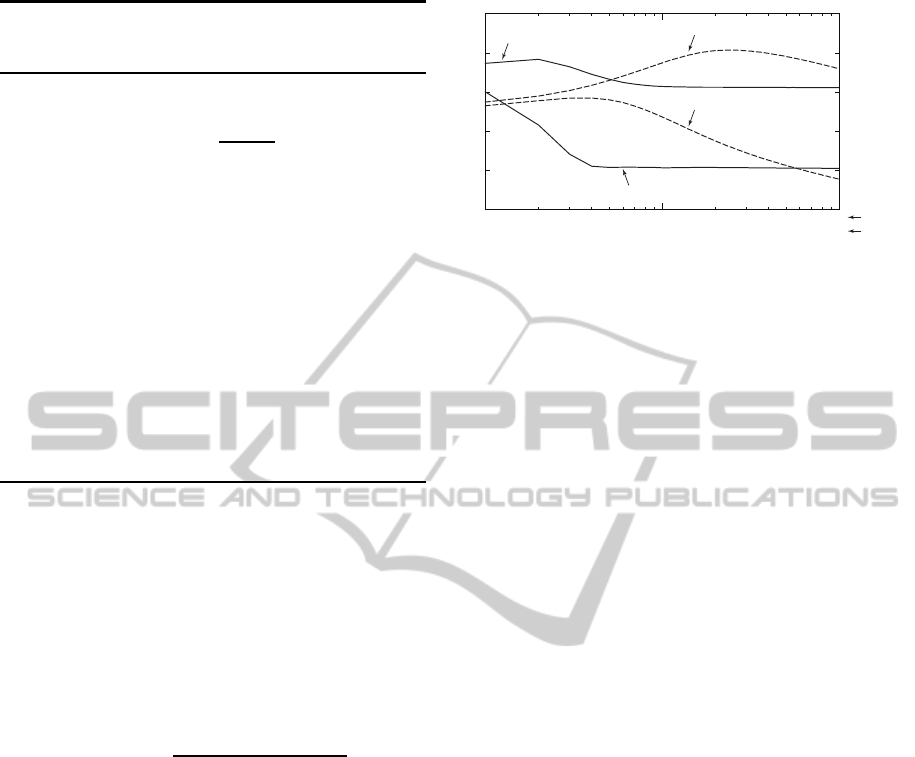
Figure 5 shows temporal changes of the measures

PSNR evaluating image denoising processes of the

proposed algorithm and the diffusion one. The mea-

sures show that the algorithm mostly converged at

t = 1.0 on both the artiﬁcial and real images, and the

diffusion algorithm did not converged in the range of

0 < t ≤ 10.

Let us discuss the above experimental results. The

proposed algorithm reduced noise with preserving

edges, as shown around i = 110 ∼ 120 in Fig. 4(e).

Fig. 4(f) demonstrates the process in which the al-

gorithm dynamically connected neighboring areas on

the i− k grid. In contrast to these successful results,

the proposed algorithm failed to preserve image de-

tails in Fig. 3(b), and created step-wise brightness dis-

tributions in the areas having high gradients in im-

age brightness distributions, for example, as shown

around i = 410 in Fig. 4(e). Figure 4(f) shows that the

proposed algorithm failed to obtain continuity in the

corresponding high gradient areas of the brightness.

We need to develop the algorithm so as to preserve

image details and simultaneously to support the con-

tinuity in the high gradient areas; we believe that how

to choose the width σ adaptivelyis a key point to solve

these problems.

Performance of the diffusion algorithm highly de-

pends on the stopping time, as shown in Fig. 5;

this is known as the stopping time evaluation prob-

SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications

224

lem (Mr´azek and Navara, 2003). The proposed al-

gorithm converges in enough duration of time. This

is because the FitzHugh-Nagumo type nonlinear ex-

citable element has one or two stable steady state(s),

and convergence of the uncoupled element is guaran-

teed (Murray, 1989).

4 CONCLUSION

This paper presented an image denoising algorithm,

which consists of a three-dimensional grid system of

coupled FitzHugh-Nagumo type nonlinear excitable

elements. In particular, each element is externally

stimulated so as to ﬁt the grid system to the task of

image denoising. The PSNR measure evaluated per-

formance of the algorithm in comparison with the two

other classical algorithms of a diffusion equation and

median ﬁltering on artiﬁcial and real images. As the

results, although the overall performance of the pro-

posed algorithm did not achieve that of the other ones,

it successfully recovered image brightness distribu-

tions around edges as well as reducing noise. We be-

lieve that this is a merit of the proposedalgorithm hav-

ing nonlinearlity in comparison with the other ones.

The convergence of the proposed algorithm was nu-

merically conﬁrmed.

ACKNOWLEDGEMENTS

This work was supported by JSPS KAKENHI Grant

Number 26330276.

REFERENCES

Buades, A., Coll, B., and Morel, J. M. (2010). Image de-

noising methods. A new nonlocal principle. SIAM Re-

view, 52:113–147.

Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.

(2007). Image denoising by sparse 3-d transform-

domain collaborative ﬁltering. IEEE Transactions on

Image Processing, 16:2080–2095.

Eng, H.-L. and Ma, K.-K. (2001). Noise adaptive soft-

switching median ﬁlter. IEEE Transactions on Image

Processing, 10:242–251.

FitzHugh, R. (1961). Impulses and physiological states in

theoretical models of nerve membrane. Biophysical

Journal, 1:445–466.

Gonzalez, R. C. and Woods, R. E. (1992). Digital Image

Processing. Addison-Wesley, New York, USA.

Guo, Z., Liu, Q., Sun, J., and Wu, B. (2011). Reaction-

diffusion systems with p(x)-growth for image denois-

ing. Nonlinear Analysis: Real World Applications,

12:2904–2918.

Heath, M., Sarkar, S., Sanocki, T., and Bowyer,

K. (conﬁrmed on June 1st, 2014). Edge

detector comparison. Available from:

http://marathon.csee.usf.edu/edge/edge

detection.html.

Katkovnik, V., Foi, A., Egiazarian, K., and Astola, J.

(2010). From local kernel to nonlocal multiple-model

image denoising. International Journal of Computer

Vision, 86:1–32.

Koenderink, J. J. (1984). The structure of images. Biologi-

cal Cybernetics, 50:363–370.

Mr´azek, P. and Navara, M. (2003). Selection of optimal

stopping time for nonlinear diffusion ﬁltering. Inter-

national Journal of Computer Vision, 52:189–203.

Murray, J. D. (1989). Mathematical Biology. Springer-

Verlag, Berlin, Germany.

Nagumo, J., Arimoto, S., and Yoshizawa, S. (1962). An

active pulse transmission line simulating nerve axon.

Proceedings of the IRE, 50:2061–2070.

Nomura, A., Ichikawa, M., Okada, K., Miike, H., and Saku-

rai, T. (2011). Edge detection algorithm inspired by

pattern formation processes of reaction-diffusion sys-

tems. International Journal of Circuits, Systems and

Signal Processing, 5:105–115.

Nomura, A., Okada, K., Mizukami, Y., Miike, H., Ichikawa,

M., and Sakurai, T. (2012). Subpixel stereo dis-

parity for surface reconstruction by utilising a three-

dimensional reaction-diffusion system. In Proceed-

ings of the 27th Image and Vision Computing New

Zealand Conference, pages 144–149, Dunedin, New

Zealand.

Perona, P. and Malik, J. (1990). Scale-space and edge de-

tection using anisotropic diffusion. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

12:629–639.

Tomasi, C. and Manduchi, R. (1998). Bilateral ﬁltering for

gray and color images. In Proceedings of the 1998

IEEE International Conference on Computer Vision,

pages 839–846, Bombay, India.

ImageDenoisingAlgorithmwithaThree-dimensionalGridSystemofCoupledNonlinearElements

225