
Smoothed Surface Transitions for Human Motion Synthesis
Ashish Doshi
iMinds, EDM, University of Hasselt, Wetenschapspark 2, 3590 Diepenbeek, Belgium
Keywords:
3D Human Motion, 3D Synthesis, 3D Surface Transition, Feature Detection.
Abstract:
Multiview techniques to reconstruct an animation from 3D video have advanced in leaps and bounds in re-
cent years. It is now possible to synthesise a 3D animation by fusing motions between different sequences.
Prior work in this area has established methods to successfully identify inter-sequence transitions of differ-
ent or similar actions. In some instances however, the transitions at these nodes in the motion path would
cause an abrupt change between the motion sequences. Hence, this paper proposes a framework that allows
for smoothing of these inter-sequence transitions, while preserving the detailed dynamics of the captured
movement. Laplacian based mesh deformation, in addition to shape and appearance based feature methods,
including SIFT and MeshHOG features, are used to obtain temporally consistent meshes. These meshes are
then interpolated within a temporal window and concatenated to reproduce a seamless transition between the
motion sequences. A quantitative analysis of the inter-sequence transitions, evaluated using three dimensional
shape based Hausdorff distance is presented for synthesised 3D animations.
1 INTRODUCTION
3D human motion synthesis is increasingly an impor-
tant part of motion animation, especially in movie,
games, tele-medicine and broadcasting industries. It
is laborious work for an animator to manually edit
an animation between different movements, i.e. mo-
tion compositing. As such, reusing captured motion
sequences to create a new animation saves time as
well as money. In (Huang et al., 2009), a 3D tem-
poral shape similarity measure was used to automati-
cally find the closest match between different motion
actions. Although not clearly visible, sometimes the
inter-sequence dynamic deformation causes an unin-
tentional discontinuity in the motion. As such, we
build on the work of (Huang et al., 2009), (de Aguiar
et al., 2008) to obtain a realistic motion deformation
that preserves the dynamic motion shape and appear-
ance at each surface transition point.
The framework presented in this paper is outlined
as follows. Figure 1(a) shows an example database of
3D video sequences obtained from either (Starck and
Hilton, 2007) or (Vlasic et al., 2008). In Figure 1(b), a
surface motion graph is constructed using 3D tempo-
ral shape similarity measures as proposed in (Huang
et al., 2009). This in turn yields an adaptive tempo-
ral window of length, N
t
which depicts the number of
frames before and after each inter-sequence transition
node to be used. If a fixed window is used, the abrupt
change would still occur in some transitions because
of the differences in speed of motion between the ac-
tion sequences.
Figure 1(c) shows surface feature matching per-
formed on inter-sequence pairs within the window.
Appearance based multiview correspondences are de-
tected using SIFT (de Aguiar et al., 2008),(Lowe,
2003) in the 2D image domain and using Mesh-
HOG (Zaharescu et al., 2009) from the 3D surface
geometry. This combination of features has proved
to be most consistent for 3D surface feature matching
and tracking. Robust matching is then obtained be-
tween pairs of frames between the sequences within
the transition window.
Matching correspondences are used as soft con-
straints for a volumetric mesh deformation which
tetrahedralises the source mesh and then warp to
fit the target mesh, as shown in Figure 1(d). The
main purpose of using volumetric mesh deformation
is to obtain a consistent mesh structure for the inter-
sequence frames. Figure 1(e) shows a synthesised
interpolated 3D mesh extracted between the source
and target meshes based on the corresponding blend-
ing weight that fit within the framework. Finally,
a collection of linear interpolations between the se-
quences within the window is concatenated to obtain
a dynamic smoothed motion between the sequences
73
Doshi A..
Smoothed Surface Transitions for Human Motion Synthesis.
DOI: 10.5220/0005122400730079
In Proceedings of the 11th International Conference on Signal Processing and Multimedia Applications (SIGMAP-2014), pages 73-79
ISBN: 978-989-758-046-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
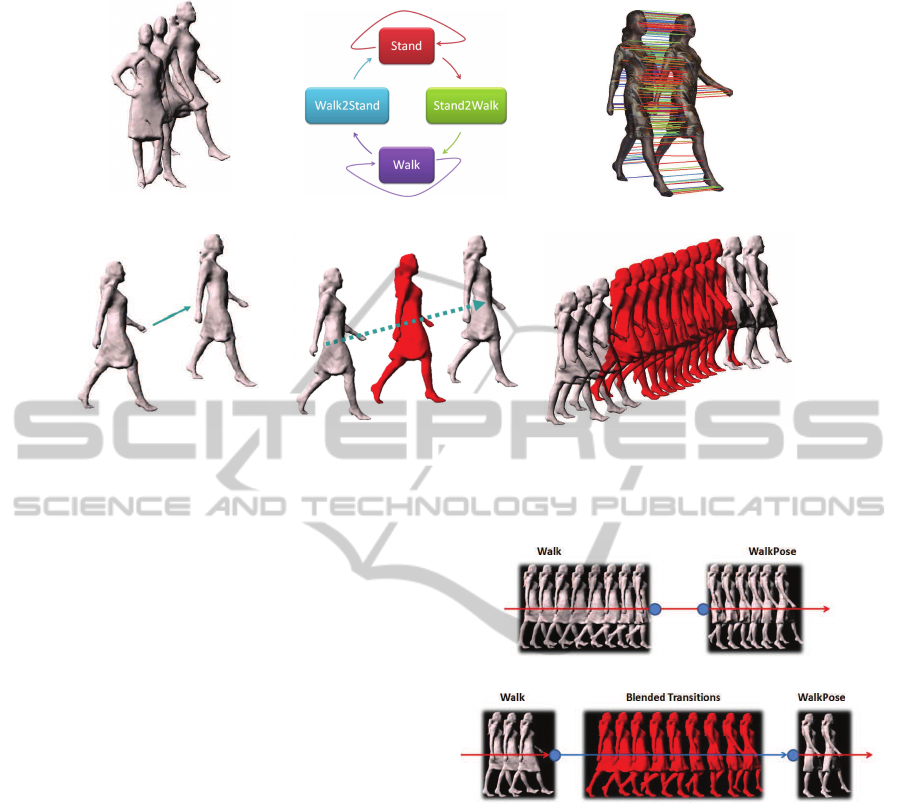
(a) 3D video sequence (b) Surface motion graph (c) Surface feature matches
(d) Mesh deformation (e) Mesh interpolation (f) 3D synthesis
Figure 1: Different consecutive steps of the smoothed motion path framework: (a) input 3D video database; (b) surface
motion graph; (c) surface feature matching from SIFT and MeshHOG; (d) mesh deformation; (e) mesh interpolation; (f) new
3D animation with blended meshes in red.
as presented in Figure 1(f). The final outcome will
be a new 3D video animation. A side-view example
of standard and temporally smoothed transitions be-
tween the sequences is shown in Figure 2.
Figure 2(a) shows the transition between
Walk and WalkPose sequences from the Fashion1
dataset (Starck and Hilton, 2007). The transition
occurs between frame 38 of Walk sequence and
frame 23 of WalkPose sequence as indicated by
blue nodes in the figure. In comparison, Figure 2(b)
shows the transition between Walk and WalkPose
sequences with temporal blending. However, instead
of the transition occuring at frame 38 of the Walk
sequence, it now occurs over a window between
frame 33 and frame 27 of the WalkPose sequence.
The meshes in red indicate interpolated meshes
between frames from Walk and its correponding
frames in the WalkPose sequence within the temporal
window.
Prior work as presented in Section 2 suggests
that synthesising a new 3D video sequence from a
database of available 3D video sequences is possible.
However, the inter-sequence transitions in the video
remain choppy especially with significant dynamic
change of the surface geometry and would need user
intervention to generate smooth transitions. The pur-
pose of this paper is to present a novel framework of
post-processing surface geometry that combines the
best of 3D human motion synthesis, surface feature
matching, mesh deformation and interpolation (Sec-
tion 3) to obtain a smooth 3D video sequence that
(a) Without blending
(b) With temporal motion blending
Figure 2: Inter-sequence transitions between Walk and
WalkPose sequences: (a) Walk frames 31-38, WalkPose
frames 23-28; (b) Walk frames 31-33, Blended frames
{34(Walk),18(WalkPose)}-{42(Walk),26(WalkPose)},
WalkPose frames 27-28.
preserves the dynamic movement of the surface. Re-
sults and quantitative analysis is presented in Sec-
tion 5 with conclusions drawn from this work high-
lighted in Section 6.
2 RELATED WORK
Concatenating physically simulated and scripted mo-
tion is a tricky task, even for an experienced anima-
tor. Hence, motion editing of temporal and dynamic
unstructured mesh sequences remains an open and
SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications
74

challenging problem. Similar to the 3D motion com-
positing, (Sch¨odl et al., 2000) used temporal similar-
ity based metrics between still frames to subsequently
create a new video sequence. They suggested that it
is not possible to extend 2D similarity based metrics
to 3D deformable surfaces.
Starck et.al. (Starck et al., 2005) proposed an ani-
mation control algorithm based on motion graph and
spherical matching method to optimise mesh blend-
ing. Their motion blending approach incorporates a
coarse-to-fine optimisation algorithm which is depen-
dent on multiview surface correspondences. In ad-
dition, Kircher and Garland (Kircher and Garland,
2008) discusses the virtues of absolute, linear and rel-
ative blending methods for dynamic meshes in their
method. Their proposed method is based on using tri-
angles instead of the standard vertex based blending,
which has been shown to yield excellent results.
Interestingly, Baran et.al. (Baran et al., 2009) sug-
gested using semantic based correspondences to de-
form a mesh based on its relative movement. In con-
trast, Xu et.al. (Xu et al., 2009) proposed using mod-
ified Dijkstra algorithm in the motion graph to gen-
erate new animation, though their method does have
the limitation that they allow large discontinuities be-
tween transitions, as long as it is visually accept-
able. Hsieh et.al. (Hsieh et al., 2005) proposed us-
ing a skeletal correspondences to help in the blend-
ing of transition nodes. The workflow that they pre-
sented is based on using user-defined skeletal infor-
mation. Their method reduces the surface geometry
to metaskeletons which they are able to match be-
tween poses of different action sequences. Similarly,
Arikan et.al (Arikan and Forsyth, 2002) proposed mo-
tion synthesis of articulated data by concatenating
frames from a database. They also use similarity mea-
sures for matching skeletal data. Other prior work
that uses skeletal data for concatenative synthesis of
human motion is presented in (Kovar et al., 2002).
Mesh deformation using volumetric based meth-
ods is actually quite a common thing to do (de Aguiar
et al., 2008; Zhou et al., 2005), since this maintains
the volume of the mesh and preserves fine details of
the surface geometry. A typical technique is using the
graph Laplacian method. However, when applied to
large deformations with insufficient constraints, facet
pinching and intersection artifacts become apparent.
Hence, the motivation to perform mesh interpolation
based on feature correspondences to ensure non-rigid
shape and dynamic preservation.
3 HUMAN MOTION SYNTHESIS
Transition points between 3D video sequences are
identified without temporal correspondences using a
3D shape similarity metric. The motion synthesis is
dependent on two stages. The first is construction of
the surface motion graph which is used to identify
possible inter-sequence transitions and the second, a
motion path optimisation algorithm that satisfies user
defined constraints.
Motion sysnthesis is obtained by minimising the
transition cost between keyframes whilst observing
spatial and temporal constraints. The transition cost
is dependent on three measures, i.e. total transition
cost, C
s
(F) which is the sum of all dissimilarities of
transitions concatenated for the path F, distance cost,
C
d
(F) defined as the difference between target dis-
tance and travelled distance along the path and time
cost, C
t
(F) defined as difference between user speci-
fied target time and actual travelled time. Hence, the
transition cost is
C(F) = C
s
(F) + w
d
C
d
(F) + w
t
C
t
(F) (1)
with w
d
and w
t
being weights for distance and time re-
spectively. The optimised path for the motion synthe-
sis is found by minimising the cost function in Equa-
tion (1), i.e.
F
opt
= argmin
F
{C(F)} (2)
Further details of solving Equation (2) using Inte-
ger Linear Programming (ILP) method can be found
in (Huang et al., 2009).
4 SMOOTH MOTION
TRANSITION
Figure 3 shows the process of obtaining smooth mo-
tion transitions between sequences. For example,
A represents the Walk sequence and B represents
the Stand2Walk sequence of a surface captured game
character. The numbers in each node represent the
frame position in the sequence. The star (*) in Fig-
ure 3 shows where the initial transition nodes are that
would switch the sequence from A to B. The frames
that represent each of these nodes is shown in Fig-
ure 2. It can be observed that when the transition
occurs between frame 25 and 56, a discontinuity ap-
pears. Therefore, there is a need to obtain a blending
path that is smooth and progressivelypropagates from
sequence A to B.
SmoothedSurfaceTransitionsforHumanMotionSynthesis
75

Figure 3: Smooth motion path: In green is sequence A with
its respective numbered nodes, blue is sequence B with its
respective numbered nodes. Orange boxes highlight pair-
wise frames for robust multiview feature matching. Black
arrows show direction for interpolation, with source having
higher blending weight. Red arrows show path of deforma-
tion. ’*’ marks the optimised transition nodes.
4.1 Surface Feature Matching
For the transition to occur between frames 25 and 56
of this example, an optimal window length, n = 5 is
obtained from (Huang et al., 2009). Robust sparse
multiview correspondences between pairwise texture
images, I
k
c
are obtained, with I and c representing an
image and camera number respectively and k depict-
ing frame number. The correspondences are obtained
using SIFT
1
and 3D MeshHOG (Zaharescu et al.,
2009), and is pruned through matching as follows
dd
k
c,e
(p,q) =k f
k
c,p
− f
ˆ
k
c,q
k ∀p ∈ f
k
c
,q ∈ f
ˆ
k
c
(3)
where dd
k
c,e
(p,q) is the Euclidean distance list be-
tween two feature descriptor sets in each camera view,
f
k
c,p
in the source frame and f
ˆ
k
c,q
in the target frame.
Matched features are obtained using nearest neigh-
bour method
dd
e
(p,q) ≤ βdd
e
(p,q+ 1) ∀p ∈ f
k
c
,q ∈ f
ˆ
k
c
(4)
and is projected to 3D space. The nearest neighbour
ratio, β is typically set at 0.4. Only mutually con-
sistent correspondences which are bijective is kept.
Though not included here, a detailed analysis of fea-
ture detection and matching for 3D human motion
from video can be found in (Doshi et al., 2010).
4.2 Mesh Deformation & Interpolation
It is assumed that the surface captured 3D meshes
used are unstructured. In order to obtain a reliable
interpolation of the mesh, both the source and the tar-
get meshes have to be structured. This is performed
1
SIFT source obtained from http://www.vlfeat.org
by first tetrahedralising the source mesh, M
k
yield-
ing a tetraheral mesh, M
k
T
which is volumetric. This
means that if M
k
T
is deformed either translationally
or rotationally, the Laplacian deformation technique
preserves the volume of the mesh.
Next, a volumetric Laplacian mesh deformation
technique (Sorkine, 2006) is applied to obtain the syn-
thesised target mesh M
ˆ
k
following
argmin
v
{k Lv− L
ˆ
v
k
k
2
} (5)
where L represents the graph Laplacian operator con-
structed from source mesh vertices,
ˆ
v is the vertex
location of the target mesh, v is the vertex location
of the source mesh and
ˆ
v
k
are the sparse constraints
(from previous section) to warp the source mesh to
target mesh.
In order to obtain a smooth motion path between
the sequences, it is pertinent that the dynamic meshes
being warped are of consistent structures. With both
the source and target meshes having the same struc-
ture, it is easier to perform interpolation. As per stan-
dard practice, a linear blending method as shown in
Equation (6) is used to obtain interpolated meshes.
z
i
= (1− α
i
)a
i
+ α
i
b
i
(6)
where z
i
denotes the blended frame and α
i
is the
blending weight for the corresponding source and tar-
get meshes.
Although the computation of blending weight is
trivial, it remains an important step as this determines
how much the source and target meshes are to be in-
terpolated. The blending weight, α is set as the in-
verse of the optimised window length, n
opt
. Hence,
for each frame set, α is shown to be
α
i
=
k
i
2n
opt
+ 1
∀i = K − n
opt
,... ,K + n
opt
(7)
with K depicting the center frame of the dynamic
window. Therefore, for the example shown in Fig-
ure 2(b), n
opt
= 4. Hence, the blending weights for
the meshes within the window in Figure 2(b) will be
α
i
= {1/N
T
,..., N
T
/N
T
}, with N
T
= 2∗ n
opt
+ 1 rep-
resenting the total size of the window.
5 RESULTS & DISCUSSION
Synthesised character animations are created from
a publicly available 3D video database (Starck and
Hilton, 2007). The database consists of four character
sets; (1) Character 1 - game character, (2) Fashion 1
- fully textured long flowing dress and (3) Fashion 2 -
shorter, plain and tighter fitting dress, all of which are
SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications
76
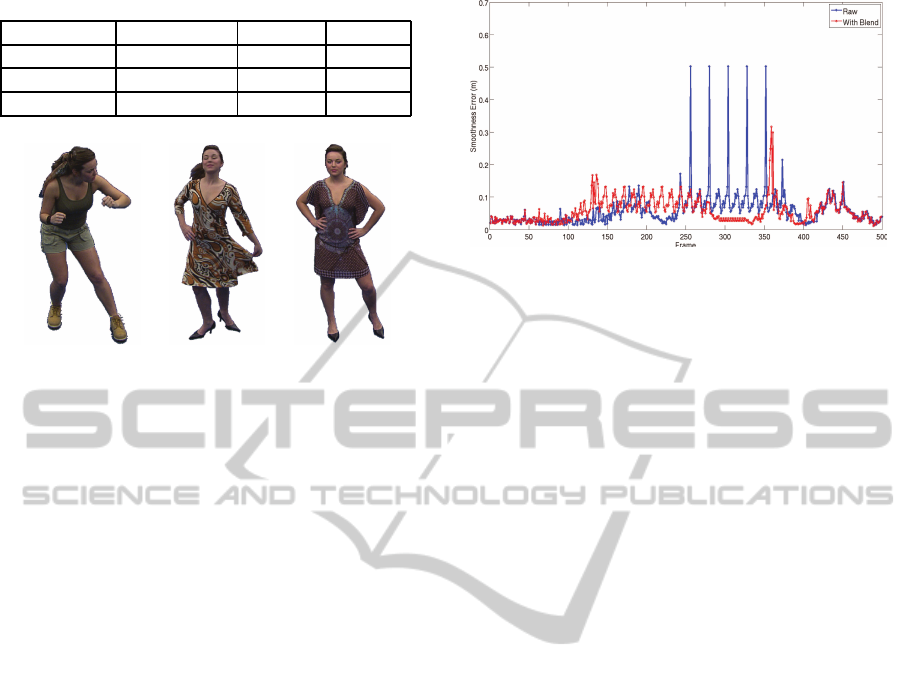
Table 1: Information on 3D video sequences used.
3D Seq. Action Seq. Frames Images
Character1 10 442 3536
Fashion1 6 418 3344
Fashion2 6 432 3456
(a) Character1 (b) Fashion1 (c) Fashion2
Figure 4: Example frames from the 3D video database.
challenging for re-animation. The characteristics of
the datasets used is presented in Table 1 with example
frames for each dataset shown in Figure 4.
A total of over 3000 meshes (>100k vertices each)
and over 30000 texture images (from 8 cameras) have
been used to construct surface motion graphs. From
the motion graphs, three test 3D animations havebeen
synthesised for analysis.
The smoothness error, measured in centimetres is
evaluated using the Metro (Cignoni et al., 1998) tool
which calculates the Hausdorff distance between two
surfaces in three dimensional space using
H(S
i
,
ˆ
S
j
) = max{h(S
i
,
ˆ
S
j
),h(
ˆ
S
j
,S
i
)} . (8)
where
h(S
i
,
ˆ
S
j
) = max
v∈S
i
min
ˆv∈
ˆ
S
j
kv− ˆvk . (9)
where v and ˆv are vertices of the source surface geom-
etry S
i
and of reference surface
ˆ
S
j
, respectivelywithin
the synthesised animation sequence, and k · k denotes
the Euclidean distance between the vertices in spatial
space. i and j are surface transition indices within the
synthesised 3D video sequence.
The graph in Figure 5 shows the error between
successive frames in the Fashion2 synthesised 3D
video sequence. Because the female model is moving
slowly in the beginning, the change between the sur-
faces is reasonably low. However, as she starts walk-
ing at approximately the 120th frame of the sequence,
the error increases because of the differences between
the surface geometry. The largest spike in the raw se-
quence, with error of 50.17cm occurs at a point when
the model is walking with larger footsteps. From the
figure, sequential patterns of peaks and troughs is due
to motion loops occuring. Smoothness errors for the
Figure 5: Fashion2: Graph of smoothness error between
successive frames in the 3D synthesised animation.
blended sequences is highlighted in red. The differ-
ence in change of error is apparent between the raw
and blended sequences.
Spikes in the blended squence which do not have
a corresponding spike in the raw sequence relate to
large changes between the frames. It is worth not-
ing that for mesh deformation to work properly, the
surface correspondences has to be as accurate as pos-
sible. Even with minimal inaccuracies, the mis-
matches can cause abnormal deformations, i.e. facet
self-intersections or collapsing faces. Another impor-
tant fact is that if a geometry causes an irregular dis-
tribution of the correspondences, then it is likely that
the output from the mesh deformation would also ex-
hibit abnormal deformity in some regions of the sur-
face. All these situations can cause 3D synthesis er-
rors which in turn means large changes between the
frames can occur. This can be related to the spikes in
the blended squence which do not have a correspond-
ing spike in the raw sequence.
An error distribution snapshot between frames
292 and 299 of the graph in Figure 5 is presented
in Figure 6. The colour distribution in the fig-
ure is highlighted as: < 3cm → Red to Yellow; <
6cm → Yellow to Green; < 9cm → Green to Cyan;
< 12cm → Cyan to Blue and Blue for errors larger
than 12cm. It can be seen that large error occurs when
there is large movement present. The motion in the
sequences at these correponding frames differ signif-
icantly, i.e. in Figure 6(a), the model is still walking
and in Figure 6(b), the model is standing still. By
using blended frames in the sequence, it is shown
(Figure 5) that the model have been synthesised to
stop walking earlier in the sequence and is standstill,
whilst the model is about to stop walking in the raw
sequence.
SmoothedSurfaceTransitionsforHumanMotionSynthesis
77

(a) Fashion2: Raw sequence frames 292-299
(b) Fashion2: Blended sequence frames 292-299
Figure 6: Smoothness error distribution on the surface between frames.
6 CONCLUSIONS
In conlusion, the process that have been presented
provides a smooth motion path for concatenation of
human motion synthesis from 3D video sequences.
In contrast to using depth cameras (Microsoft Kinect)
and annotated markers (Flagg et al., 2009), we have
shown that in the absence of skeletal information, us-
ing automatically detected surface correspondences
from SIFT and MeshHOG, an intermediate surface
motion can be reconstructed to create a seamless mo-
tion transfer between sequences. The process in-
cludes using Laplacian mesh deformation and linear
blending methods to preserve the non-rigid dynam-
ics of the surface. Work is in progress to include ad-
ditional coarse correspondences for filling in regions
without any features to facilitate greater flexibility in
the re-use of motion sequences. Further emphasis
is being placed on making surface feature matching
temporally consistent, similar to that of (Budd et al.,
2013) which uses patch mesh, to allow reliable esti-
mation of a consistent structure.
REFERENCES
Arikan, O. and Forsyth, D. A. (2002). Interactive mo-
tion generation from examples. In ACM SIGGRAPH,
pages 483–490.
Baran, I., Vlasic, D., Grinspun, E., and Popovi´c, J. (2009).
Semantic deformation transfer. In ACM SIGGRAPH,
pages 1–6.
Budd, C., Huang, P., Klaudiny, M., and Hilton, A. (2013).
Global non-rigid alignment of surface sequences. In-
ter. Journal of Computer Vision, 102(1-3):256–270.
Cignoni, P., Rocchini, C., and Scopigno, R. (1998). Metro:
measuring error on simplified surfaces. Computer
Graphics Forum, 17(2):167–174.
de Aguiar, E., Stoll, C., Theobalt, C., Ahmed, N., Seidel,
H.-P., and Thrun, S. (2008). Performance capture
from sparse multi-view video. In ACM SIGGRAPH.
Doshi, A., Starck, J., and Hilton, A. (2010). An empirical
study of non-rigid surface feature matching of human
from 3d video. Journal of Virtual Reality and Broad-
casting, 7(2010)(3).
Flagg, M., Nakazawa, A., Zhang, Q., Kang, S. B., Ryu,
Y. K., Essa, I., and Rehg, J. M. (2009). Human video
textures. In Symposium on Interactive 3D Graphics
and Games, pages 199–206.
Hsieh, M.-K., Chen, B.-Y., and Ouhyoung, M. (2005). Mo-
tion retargeting and transition in different articulated
figures. In 9th Inter. Conf. on Computer Aided Design
and Computer Graphics.
Huang, P., Hilton, A., and Starck, J. (2009). Human motion
synthesis from 3D video. In IEEE Conf. on Computer
Vision and Pattern Recognition.
Kircher, S. and Garland, M. (2008). Free-form motion pro-
cessing. ACM Transactions on Graphics, 27(2):1–13.
Kovar, L., Gleicher, M., and Pighin, F. (2002). Motion
graphs. In ACM SIGGRAPH.
Lowe, D. (2003). Distinctive image features from scale-
invariant keypoints. Inter. Journal of Computer Vision,
20:91–110.
Sch¨odl, A., Szeliski, R., Salesin, D., and Essa, I. A. (2000).
Video textures. In ACM SIGGRAPH, pages 489–498.
Sorkine, O. (2006). Differential representations for mesh
processing. Computer Graphics Forum, 25(4):789–
807.
Starck, J. and Hilton, A. (2007). Surface capture for per-
formance based animation. Computer Graphics and
Applications, 27(3):21–31.
Starck, J., Miller, G., and Hilton, A. (2005). Video-based
character animation. In Symposium on Computer An-
imation.
SIGMAP2014-InternationalConferenceonSignalProcessingandMultimediaApplications
78

Vlasic, D., Baran, I., Matusik, W., and Popovi´c, J. (2008).
Articulated mesh animation from multi-view silhou-
ettes. ACM Transactions on Graphics, 27(3):97.
Xu, J., Yamasaki, T., and Aizawa, K. (2009). Motion edit-
ing for time-varying mesh. EURASIP Journal on Ad-
vances in Signal Processing, 2009.
Zaharescu, A., Boyer, E., Varanasi, K., and Horaud, R. P.
(2009). Surface feature detection and description
with applications to mesh matching. In IEEE Conf.
on Computer Vision and Pattern Recognition, Miami
Beach, Florida.
Zhou, K., Huang, J., Snyder, J., Liu, X., Bao, H., Guo, B.,
and Shum, H.-Y. (2005). Large mesh deformation us-
ing the volumetric graph Laplacian. ACM Transac-
tions on Graphics, 24(3):496–503.
SmoothedSurfaceTransitionsforHumanMotionSynthesis
79
