
Information Granules Filtering for Inexact Sequential Pattern Mining by
Evolutionary Computation
Enrico Maiorino
1
, Francesca Possemato
1
, Valerio Modugno
2
and Antonello Rizzi
1
1
Dipartimento di Ingegneria dell’Informazione, Elettronica e Telecomunicazioni (DIET)
SAPIENZA University of Rome, Via Eudossiana 18, 00184, Rome, Italy
2
Dipartimento di Ingegneria Informatica, Automatica e Gestionale (DIAG)
SAPIENZA University of Rome, Via Ariosto 25, 00185, Rome, Italy
Keywords:
Granular Modeling, Sequence Data Mining, Inexact Sequence Matching, Frequent Subsequences Extraction,
Evolutionary Computation
Abstract:
Nowadays, the wide development of techniques to communicate and store information of all kinds has raised
the need to find new methods to analyze and interpret big quantities of data. One of the most important
problems in sequential data analysis is frequent pattern mining, that consists in finding frequent subsequences
(patterns) in a sequence database in order to highlight and to extract interesting knowledge from the data at
hand. Usually real-world data is affected by several noise sources and this makes the analysis more challeng-
ing, so that approximate pattern matching methods are required. A common procedure employed to identify
recurrent patterns in noisy data is based on clustering algorithms relying on some edit distance between subse-
quences. When facing inexact mining problems, this plain approach can produce many spurious patterns due
to multiple pattern matchings on the same sequence excerpt. In this paper we present a method to overcome
this drawback by applying an optimization-based filter that identifies the most descriptive patterns among those
found by the clustering process, able to return clusters more compact and easily interpretable. We evaluate the
mining system’s performances using synthetic data with variable amounts of noise, showing that the algorithm
performs well in synthesizing retrieved patterns with acceptable information loss.
1 INTRODUCTION
Nowadays, sequence data mining is a very interest-
ing field of research that is going to be central in the
next years due to the growth of the so called “Big
Data” challenge. Moreover, available data in differ-
ent application fields consist in sequences (for exam-
ple over time or space) of generic objects. Gener-
ally speaking, given a set of sequences defined over
a particular domain, a data mining problem consists
in searching for possible frequent subsequences (pat-
terns), relying on inexact matching procedures. In
this work we propose a possible solution for the so
called approximate subsequence mining problem, in
which we admit some noise in the matching process.
As an instance, in computational biology, searching
for recurrent patterns is a critical task in the study
of DNA, aiming to identify some genetic mutations
or to classify proteins according to some structural
properties. Sometimes the process of pattern extrac-
tion returns sequences that differ from the others in a
few positions. Then it is not difficult to understand
that the choice of an adequate dissimilarity measure
becomes a critical issue when we want to design an
algorithm able to deal with this kind of problems.
Handling sequences of objects is another challenging
aspect, especially when the data mining task is de-
fined over a structured domain of sequences. Think-
ing data mining algorithms as a building block of a
wider system facing a classification task, a reason-
able way to treat complex sequential data is to map
sequences to R
d
vectors by means of some feature
extraction procedures in order to use classification
techniques that deal with real valued vectors as in-
put data. The Granular Computing (GrC) (Bargiela
and Pedrycz, 2003) approach offers a valuable frame-
work to fill the gap between the input sequence do-
main and the features space R
d
and relies on the so-
called information granules that play the role of indis-
tinguishable features at a particular level of abstrac-
tion adopted for system description. The main ob-
jective of Granular modeling consists in finding the
correct level of information granulation that best de-
scribes the input data. The problem of pattern data
104
Maiorino E., Possemato F., Modugno V. and Rizzi A..
Information Granules Filtering for Inexact Sequential Pattern Mining by Evolutionary Computation.
DOI: 10.5220/0005124901040111
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 104-111
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

mining is similar to the problem of mining frequent
item sets and subsequences. For this type of problem
many works (Zaki, 2001) (Yan et al., 2003) describe
search techniques for non-contiguous sequences of
objects. For example, the first work (Agrawal and
Srikant, 1995) of this sub-field of data mining is re-
lated to the analysis and prediction of consumer be-
haviour. In this context, a transaction consists in the
sale of a set of items and a sequence is an ordered
set of transactions. If we consider, for instance, a se-
quence of transactions ha, b, a, c, a, ci a possible non-
contiguous subsequence could be ha, b, c, ci. How-
ever, this approach is not ideal when the objective is
to extract patterns where the contiguity of the com-
ponent objects inside a sequence plays a fundamental
role in the extraction of information. The computa-
tion biology community has developed a lot of meth-
ods for detecting frequent patterns that in this field are
called motifs. Some works (Sinha and Tompa, 2003),
(Pavesi et al., 2004) use Hamming distances to search
for recurrent motifs in data. Other works employ suf-
fix tree data structure (Zhu et al., 2007), suffix array
to store and organize the search space (Ji and Bai-
ley, 2007), or use a GrC framework for the extrac-
tion of frequent patterns in data (Rizzi et al., 2013).
Most methods focus only on the recurrence of pat-
terns in data without taking into account the concept
of “information redundancy”, or, in other words, the
existence of overlapping among retrieved patterns. In
this paper we present a new approximate subsequence
mining algorithm called FRL-GRADIS (Filtered Re-
inforcement Learning-based GRanular Approach for
DIscrete Sequences) aiming to reduce the information
redundancy of RL-GRADIS (Rizzi et al., 2012) by ex-
ecuting an optimization-based refinement process on
the extracted patterns. In particular, this paper intro-
duces the following contributions:
1. our approach finds the patterns that maximize the
knowledge about the process that generates the se-
quences;
2. we employ a dissimilarity measure that can ex-
tract patterns despite the presence of noise and
possible corruptions of the patterns themselves;
3. our method can be applied on every kind of se-
quence of objects, given a properly defined simi-
larity or dissimilarity function defined in the ob-
jects domain;
4. the filtering operation produces results that can be
interpreted more easily by application’s field ex-
perts;
5. considering this procedure as an inner module of
a more complex classification system, it allows to
further reduce the dimension of the feature space,
thus better addressing the curse of dimensionality
problem.
This paper consists of three parts. In the first part we
provide some useful definitions and a proper notation;
in the second part we present FRL-GRADIS as a two-
step procedure, consisting of a subsequences extrac-
tion step and a subsequences filtering step. Finally, in
the third part, we report the results obtained by apply-
ing the algorithm to synthetic data, showing a good
overall performance in most cases.
2 PROBLEM DEFINITION
Let D = {α
i
} be a domain of objects α
i
. The objects
represent the atomic units of information. A sequence
S is an ordered list of n objects that can be represented
by the set of pairs
S = {(i → β
i
) | i = 1, ... , n; β
i
∈ D},
where the integer i is the order index of the object β
i
within the sequence S. S can also be expressed with
the compact notation
S ≡ hβ
1
, β
2
, ..., β
n
i
A sequence database SDB is a set of sequences S
i
of
variable lengths n
i
. For example, the DNA sequence
S = hG, T,C, A, A, T, G, T,Ci is defined over the do-
main of the four amino acids D = {A,C, G, T }.
A sequence S
1
= hβ
0
1
, β
0
2
, ..., β
0
n
1
i is a subsequence
of a sequence S
2
= hβ
00
1
, β
00
2
, ..., β
00
n
2
i if n
1
≤ n
2
and
S
1
⊆ S
2
. The position π
S
2
(S
1
) of the subsequence S
1
with respect to the sequence S
2
corresponds to the or-
der index of its first element (in this case the order
index of the object β
0
1
) within the sequence S
2
. The
subsequence S
1
is also said to be connected if
β
0
j
= β
00
j+k
∀ j = 1, ..., n
1
where k = π
S
2
(S
1
).
Two subsequences S
1
and S
2
of a sequence S are over-
lapping if
S
1
∩ S
2
6=
/
0.
In the example described above, the complete nota-
tion for the sequence S = hG, T,C, A, A, T, G, T,Ci is
S = {(1 → G), (2 → T ), (3 → C),...}
and a possible connected subsequence S
1
= hA, T, Gi
corresponds to the set
S
1
= {(5 → A), (6 → T ), (7 → G)}.
Notice that the objects of the subsequence S
1
inherit
the order indices from the containing sequence S, so
that they are univocally referred to their original po-
sitions in S. From now on we will focus only on con-
nected subsequences, therefore the connection prop-
erty will be implicitly assumed.
InformationGranulesFilteringforInexactSequentialPatternMiningbyEvolutionaryComputation
105

β
1
β
2
β
3
β
4
β
5
β
6
β
7
β
6
β
8
. . . . . .
ω
3
ω
2
ω
1
ω
4
ω
5
S
Ω
C
Figure 1: Coverage of the pattern Ω over the subsequence C ⊆ S with tolerance δ. Black boxes and gray boxes represent
respectively the covered and the uncovered objects of the sequence S. Notice that if δ > 0 the sequences Ω and C need not to
be of the same length.
G G
T T
A
C G
T
C
T
C G G G
A
C G G
T
G
T
C
T
G G C
A A
C G G
T
C
T T
G
A
G G
T
A
G G
T
A
G G
T
Figure 2: Coverage examples in the case of DNA sequences. The searched pattern hA,G,G, T i is found 3 times with tolerance
δ ≤ 1 using the Levenshtein distance. The three occurrences show all the edit operations allowed by the considered edit
distance, respectively objects substitution, deletion and insertion.
2.1 Pattern Coverage
The objective of this algorithm is to find a set
of frequent subsequences of objects named as pat-
terns. A pattern Ω is a subsequence of objects
hω
1
, ω
2
, ..., ω
|Ω|
i, with ω
i
∈ D, that is more likely to
occur within the dataset SDB. Patterns are unknown a
priori and represent the underlying information of the
dataset records. Moreover, each sequence is subject
to noise whose effects include the addition, substitu-
tion and deletion of objects in a random uncorrelated
fashion and this makes the recognition of recurrent
subsequences more challenging.
Given a sequence S ∈ SDB and a set of patterns
Γ = {Ω
1
, ..., Ω
m
}, we want to determine a quality cri-
terion for the description of S in terms of the pattern
set Γ. A connected subsequence C ⊆ S is said to be
covered by a pattern Ω ∈ Γ iff d(C, Ω) ≤ δ, where
d(·, ·) is a properly defined distance function and δ is
a fixed tolerance (Fig. 1). The coverage C
(δ)
Ω
(S) of
the pattern Ω over the sequence S is the union set of
all non-overlapping connected subsequences covered
by the pattern. We can write,
C
(δ)
Ω
(S) =
[
i
h
C
i
⊆ S s.t.
d(C
i
, Ω) ≤ δ ∧ C
i
∩C
j
=
/
0 ∀ i 6= j
i
.
(1)
Formally, this set is still not well defined until we ex-
pand on the meaning of the property
C
i
∩C
j
=
/
0, (2)
which is the requirement for the covered subse-
quences to be non-overlapping. Indeed, we need to in-
clude additional rules on how to deal with these over-
lappings when they occur. To understand better, let us
recall the example of the DNA sequences presented
above, where the dissimilarity measure between two
sequences is the Levenshtein distance. The set of all
covered subsequences C
i
(in this context referred to
as candidates) by the pattern Ω over the sequence S
will consist only of sequences with values of length
between |Ω| − δ and |Ω| + δ. Indeed, these bounds
correspond respectively to the extreme cases of delet-
ing and adding δ objects to the subsequence. In case
of two overlapping candidates C
i
and C
j
, in order to
satisfy the property (2) of the coverage C
(δ)
Ω
(S), we
have to define a rule to decide which subsequence be-
longs to the set C
(δ)
Ω
(S) and which does not. Candi-
dates with smaller distances from the searched pattern
Ω are chosen over overlapping candidates with higher
distances. If the two overlapping candidates have the
same distance the first starting from the left is cho-
sen, but if also their starting position is the same the
shorter one (i.e. smaller length value) has the prece-
dence.
A coverage example in the context of the DNA se-
quences is shown in Fig. 2. The coverage of the pat-
tern Ω = hA, G, G, T i over the sequence S is C
(δ)
Ω
(S) =
hA,C, G, T i ∪ hG, G, T i ∪ hA,C, G, G, T i.
Similarly, the compound coverage of the pattern
set Γ is defined as
C
(δ)
Γ
(S) =
[
Ω∈Γ
C
(δ)
Ω
(S). (3)
It is important to notice that, in this case, this set
can include overlapping subsequences only if they be-
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
106

A
C
T T
A
C G
T
C CC G G G
S
A
G G
T
G
T
C
Ω
2
Ω
1
Figure 3: Example of the compound coverage of multi-
ple symbols, where the symbols hG, T,Ci and hA, G, G, T i
have Levenshtein distances from the corresponding subse-
quences equal to 0 and 1, respectively. Notice that different
symbols can cover overlapping subsequences, while com-
peting coverages of the same symbol are not allowed and
only the most similar subsequence is chosen.
long to coverages of different patterns (i.e. it is as-
sumed that different patterns can overlap). For ex-
ample consider the case shown in Fig. 3. The cov-
erage C
(δ)
{Ω
1
,Ω
2
}
(S) for the patterns Ω
1
= hA, G, G, T i
and Ω
2
= hG, T,Ci is equal to C
(δ)
{Ω
1
,Ω
2
}
(S) =
hA, G, G, T,Ci.
3 THE MINING ALGORITHM
In this section, we describe FRL-GRADIS, as a
clustering-based sequence mining algorithm. It is
able to discover clusters of connected subsequences
of variable lengths that are frequent in a sequence
dataset, using an inexact matching procedure. FRL-
GRADIS consists in two main steps:
• the Symbols Alphabet Extraction, which ad-
dresses the problem of finding the most frequent
subsequences within a SDB. It is performed by
means of the clustering algorithm RL-GRADIS
(Rizzi et al., 2012) that identifies frequent sub-
sequences as representatives of dense clusters of
similar subsequences. These representatives are
referred to as symbols and the pattern set as the
alphabet. The clustering procedure relies on a
properly defined edit distance between the subse-
quences (e.g. Levenshtein distance, DTW, etc..).
However, this approach alone has the drawback of
extracting many superfluous symbols which gen-
erally dilute the pattern set and deteriorate the in-
terpretability of the produced pattern set.
• the Alphabet Filtering step deals with the problem
stated above. The objective is to filter out all the
spurious or redundant symbols contained in the
alphabet produced by the symbols extraction step.
To accomplish this goal we employ a heuristic ap-
proach based on evolutionary optimization over a
validation SDB.
One of the distinctive features of this algorithm is
its generality with respect to the kind of data con-
tained in the input sequence database (e.g., sequences
of real numbers or characters as well as sequences
of complex data structures). Indeed, both steps out-
lined above take advantage of a dissimilarity-based
approach, with the dissimilarity function being a
whatever complex measure between two ordered se-
quences, not necessarily metric.
In the following, we first describe the main aspects
of the symbols alphabet extraction procedure, then we
present the new filtering method. For more details on
the symbols alphabet construction we refer the reader
to (Rizzi et al., 2012).
3.1 Frequent Subsequences
Identification
Consider the input training dataset of sequences T =
{S
1
, S
2
, ..., S
|T |
} and a properly defined dissimilarity
measure d : T × T → R between two objects of the
training dataset (e.g., Levenshtein distance for strings
of characters). The goal of the subsequences extrac-
tion step is the identification of a finite set of sym-
bols A
e
= {Ω
1
, Ω
2
, ..., Ω
|A
e
|
},
1
computed using the
distance d(·, ·) in a free clustering procedure. The
algorithm we chose to accomplish this task is RL-
GRADIS which is based on the well-known Basic Se-
quential Algorithmic Scheme (BSAS) clustering al-
gorithm (Rizzi et al., 2012). Symbols are found by
analysing a suited set of variable-length subsequences
of T , also called n-grams, that are generated by ex-
panding each input sequence S ∈ T . The expansion is
done by listing all n-grams with lengths varying be-
tween the values l
min
and l
max
. The parameters l
min
and l
max
are user-defined and are respectively the min-
imum and maximum admissible length for the mined
patterns. The extracted n-grams are then collected
into the SDB N . At this point, the clustering proce-
dure is executed on N . For each cluster we compute
its representative, defined by the Minimum Sum of
Distances (MinSOD) technique (Rizzi et al., 2012), as
the element having the minimum total distance from
the other elements of the cluster. This technique al-
lows to represent the corresponding clusters by means
of their most characteristic elements.
The quality of each cluster is measured by its fir-
ing strength f , where f ∈ [0, 1]. Firing strengths are
used to track the dynamics describing the updating
rate of the clusters when the input stream of sub-
sequences N is analyzed. A reinforcement learn-
ing procedure is used to dynamically update the list
1
The subscript “e” stands for “extraction” as in extrac-
tion step.
InformationGranulesFilteringforInexactSequentialPatternMiningbyEvolutionaryComputation
107

of candidate symbols based on their firing strength.
Clusters with a low rate of update (low firing strength)
are discarded in an on-line fashion, along with the
processing of the input data stream N . RL-GRADIS
maintains a dynamic list of candidate symbols, named
receptors, which are the representatives of the active
clusters. Each receptor’s firing strength (i.e. the fir-
ing strength of its corresponding cluster) is dynami-
cally updated by means of two additional parameters,
α, β ∈ [0, 1]. The α parameter is used as a reinforce-
ment weight factor each time a cluster R is updated,
i.e., each time a new input subsequence is added to R .
The firing strength update rule is defined as follows:
f (R ) ← f (R ) + α(1 − f (R )). (4)
The β parameter, instead, is used to model the
speed of forgetfulness of receptors according to the
following formula:
f (R ) ← (1 − β) f (R ). (5)
The firing strength updating rules shown in
Eqs. (4) and 5 are performed for each currently iden-
tified receptor, soon after the analysis of each input
subsequence. Therefore, receptors/clusters that are
not updated frequently during the analysis of N will
likely have a low strength value and this will cause the
system to remove the receptor from the list.
3.2 Subsequences Filtering
As introduced above, the output alphabet A
e
of the
clustering procedure is generally redundant and in-
cludes many spurious symbols that make the recog-
nition of the true alphabet quite difficult.
To deal with this problem, an optimization step is
performed to reduce the alphabet size, aiming at re-
taining only the most significant symbols, i.e. only
those that best resemble the original, unknown ones.
Since this procedure works like a filter, we call the
output of this optimization the filtered alphabet A
f
and, clearly, A
f
⊂ A
e
holds. Nevertheless, it is impor-
tant for the filtered alphabet’s size not to be smaller
than the size of the true alphabet, since in this case
useful information will be lost. Let Γ ⊂ A
e
be a candi-
date subset of symbols of the alphabet A
e
and S ∈ V
a sequence of a validation SDB V . We assume the
descriptive power of the symbols set Γ, with respect
to the sequence S, to be proportional to the quan-
tity |C
(δ)
Γ
(S)| (cfr Eq. (3)), i.e. the number of ob-
jects β
i
∈ S covered by the symbols set Γ. In fact,
intuitively, a lower number of uncovered objects in
the whole SDB by Γ symbols can be considered as a
clue that Γ itself will likely contain the true alphabet.
The normalized number of uncovered objects in a se-
quence S by a pattern set Γ corresponds to the quantity
P =
|S| − |C
(δ)
Γ
(S)|
|S|
, (6)
where the operator |· | stands for the cardinality of the
set. The term P assumes the value 0 when the se-
quence S is completely covered by the pattern set Γ
and the value 1 when none of the symbols in Γ are
present in the sequence S. Notice that C
(δ)
Γ
(S) de-
pends on the parameter δ which represents the toler-
ance of the system towards the corruption of symbols’
occurrences caused by noise.
On the other hand, a bigger pattern set is more
likely to contain spurious patterns which tend to hin-
der the interpretability of the obtained results, so
smaller set sizes are to be preferred. This property
can be described with the normalized alphabet size
Q =
|Γ|
|A
e
|
, (7)
where A
e
is the alphabet of symbols extracted by
the clustering procedure described in the last sec-
tion. Clearly, the cardinality of A
e
represents an upper
bound for the size of the filtered alphabet, so the term
Q ranges from 0 to 1. The terms P and Q generally
show opposite trends, since a bigger set of symbols is
more likely to cover a bigger portion of the sequence
and vice versa.
Finding a tradeoff between these two quantities
corresponds to minimizing the convex objective func-
tion
G
(δ)
S
(Γ) = λ Q + (1 − λ) P (8)
where λ ∈ [0, 1] is a meta-parameter that weighs the
relative importance between the two constributions. It
is easy to verify that
0 ≤ G
(δ)
S
(Γ) ≤ 1. (9)
More generally, for a validation SDB V , the global
objective function is the mean value of G
(δ)
S
(Γ) over
all sequences S
i
∈ V , hence
G
(δ)
V
(Γ) =
∑
1≤i≤|V |
G
(δ)
S
i
(Γ)
|V |
(10)
and the best symbols set after the optimization
procedure is
A
f
= argmin
Γ⊂A
e
G
(δ)
S
(Γ). (11)
To solve the optimization problem described by
Eq. (11) we employ a standard genetic algorithm,
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
108

where each individual of the population is a subset
Γ of the extracted alphabet A
e
= {Ω
1
, ..., Ω
|A
e
|
}. The
genetic code of the individual is encoded as a binary
sequence E of length |A
e
| of the form
E
Γ
= he
1
, e
2
, ..., e
|A
e
|
i (12)
with
e
i
=
1 iff Ω
i
∈ Γ
0 otherwise
.
It is important not to mistake genetic codes with the
SDB sequences described earlier, even if they are both
formally defined as ordered sequences.
Given a validation dataset V and a fixed tolerance
δ, the fitness value F(E
Γ
) of each individual E
Γ
is in-
versely proportional to the value of the objective func-
tion introduced in the last paragraph, hence
F(E
Γ
) = 1 − G
(δ)
V
(Γ) (13)
The computation is then performed with standard
crossover and mutation operators between the binary
sequences and the stop condition is met when the
maximum fitness does not change for a fixed number
N
stall
of generations or after a given maximum num-
ber N
max
of iterations. When the evolution stops, the
filtered alphabet A
f
=
e
Γ is returned, where
e
Γ is the
symbols subset corresponding to the fittest individual
E
e
Γ
.
4 TESTS AND RESULTS
In this section, we present results from different ex-
periments that we designed to test the effectiveness
and performance of FRL-GRADIS in facing prob-
lems with varying complexity.
4.1 Data Generation
We tested the capabilities of FRL-GRADIS on
synthetic sequence databases composed of textual
strings. For this reason, the domain of the problem
is the English alphabet
D = {A, B,C, ..., Z}.
Modelled noise consists of random characters inser-
tions, deletions and substitutions to the original string.
For this reason a natural choice of dissimilarity mea-
sure between sequences is the Levenshtein distance,
that measures the minimum number of edit steps nec-
essary to transform one string of characters into an-
other. The dataset generator works as follows:
1. the true symbols alphabet A
t
is generated. This
alphabet consists of N
sym
symbols with lengths
normally distributed around the mean value L
sym
.
Each character is chosen in D with uniform prob-
ability and repeated characters are allowed;
2. a training SDB T and a validation SDB V re-
spectively composed of N
tr
and N
val
sequences are
generated. Each of these sequences is built by
concatenating N
symseq
symbols chosen randomly
from A
t
. Notice that generally N
symseq
> N
sym
so
there will be repeated symbols;
3. in each sequence, every symbol will be subject to
noise with probability µ. The application of noise
to a symbol in a sequence corresponds to the dele-
tion, substitution or insertion of one character to
that single instance of the symbol. This kind of
noise is referred to as intra-pattern noise;
4. a user-defined quantity of random characters is
added between instances of symbols in each se-
quence. This noise is called inter-pattern noise.
Such quantity depends on the parameter η that
corresponds to the ratio between the number of
characters belonging to actual symbols and the to-
tal number of character of the sequence after the
application of inter-pattern noise, that is,
η =
(# symbol characters)
(# total characters)
.
Notice that the amount of inter-pattern noise is in-
versely proportional to the value of η.
The generated datasets T and V are then ready to be
used as input of the FRL-GRADIS procedure. Notice
that the true alphabet A
t
is unknown in real-world ap-
plications and here is used only to quantify the perfor-
mance of the algorithm.
4.2 Quality Measures
We now introduce the quality measures used in the
following tests to evaluate the mining capabilities of
the FRL-GRADIS algorithm. These measures are
computed for the resulting alphabets obtained from
both the extraction and the filtering steps presented
in Section 3, in order to highlight the improvement
made by the filtering procedure (i.e. the improvement
of FRL-GRADIS over RL-GRADIS).
The redundance R corresponds to the ratio be-
tween the cardinality of the alphabet A and the true
alphabet A
t
, that is,
R =
|A|
|A
t
|
(14)
InformationGranulesFilteringforInexactSequentialPatternMiningbyEvolutionaryComputation
109

Clearly, since the filtering step selects a subset A
f
(fil-
tered alphabet) of the extracted alphabet A
e
, we al-
ways have that
R
f
< R
e
.
The redundance measures the amount of unnecessary
symbols that are found by a frequent pattern mining
procedure and it ranges from zero to infinite. When
R > 1 some redundant symbols have been erroneously
included in the alphabet, while when R < 1 some have
been missed, the ideal value being R = 1.
It is important to notice that the redundancy de-
pends only on the number of symbols reconstructed,
but not by their similarity with respect to the origi-
nal alphabet. For this purpose we also introduce the
mining error E, defined as the mean distance between
each symbol Ω
i
of the true alphabet A
t
and its best
match within the alphabet A, where the best match
means the symbol with the least distance from Ω
i
.
In other words, considering A
t
= {Ω
1
, ..., Ω
|A
t
|
} and
A = {
˜
Ω
1
, ...,
˜
Ω
|A|
}, the mining error corresponds to
E =
∑
i
d(Ω
i
,
˜
Ω
(i)
)
|A
t
|
(15)
where
˜
Ω
(i)
= argmin
˜
Ω∈A
d(Ω
i
,
˜
Ω).
This quantity has the opposite role of the redundancy,
in fact it keeps track of the general accuracy of recon-
struction of the true symbols regardless of the gen-
erated alphabet size. It assumes non-negative values
and the ideal value is 0. For the same reasons stated
above the inequality
E
f
≥ E
e
holds, so the extraction procedure’s mining error con-
stitutes a lower bound for the mining error obtainable
with the filtering step.
4.3 Results
We executed the algorithm multiple times for differ-
ent values of the noise parameters, to assess the differ-
ent response of FRL-GRADIS to increasing amounts
of noise. Most parameters have been held fixed for all
the tests and they are listed in table 1.
We present the results of tests performed with
µ = 0.5 and variable amounts of inter-pattern noise η.
It means that about half of the symbols in a sequence
are subject to the alteration of one character and in-
creasing amounts of random characters are added be-
tween symbols in each sequence. The results obtained
with this configuration are shown in figs. 4 and 5.
Table 1: Fixed parameters adopted for the tests. The param-
eter δ corresponds to the tolerance of the Levenshtein dis-
tance considered when calculating the coverage as in Eq. (1)
while λ weighs the two terms of the objective function of
Eq. (8). The values shown in the second part of the table re-
fer to the genetic algorithm’s parameters. N
pop
corresponds
to the population size, N
elite
is the fraction of individuals
who are guaranteed to survive and be copied to the new
population in each iteration, p
cross
and p
t
extmut are respec-
tively the crossover and mutation probabilities. The evolu-
tion terminates if N
evol
iterations have been performed or if
for a number N
stall
of iterations the maximum fitness has not
changed.
Parameter Value Parameter Value
N
tr
50 N
val
25
N
sym
5 N
symseq
10
l
min
4 l
max
12
δ 1 λ 0.5
N
pop
100 N
elite
0.1
p
cross
0.8 p
mut
0.3
N
max
100 N
stall
50
0.4 0.5 0.6 0.7 0.8 0.9 1
0
2
4
6
8
10
12
14
Redundance
η
Redundance (µ = 0.5)
Extraction (RL−GRADIS)
Filtering (FRL−GRADIS)
Figure 4: Plot of the redundance R of the extraction (RL-
GRADIS) and filtering (FRL-GRADIS) steps for µ = 0.5.
The redundancy plot in fig. 4 shows an apparently
paradoxical trend of the extraction procedure’s redun-
dancy: with decreasing amounts of inter-pattern noise
(i.e. increasing values of η) the extraction algorithm
performs more poorly, leading to higher redundan-
cies. That can be easily explainable by recalling how
the clustering procedure works.
Higher amounts of inter-pattern noise mean that
the frequent symbols are more likely to be sepa-
rated by random strings of characters. These strings
of uncorrelated characters generate very sparse clus-
ters with negligible cardinality that are very likely to
be deleted during the clustering’s reinforcement step.
Clusters corresponding to actual symbols, instead, are
more active and compact, their bounds being clearly
defined by the noise characters, and so they are more
likely to survive the reinforcement step.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
110
0.4 0.5 0.6 0.7 0.8 0.9 1
0
1
2
3
4
5
Mining Error
η
Mining error (µ = 0.5)
Extraction (RL−GRADIS)
Filtering (FRL−GRADIS)
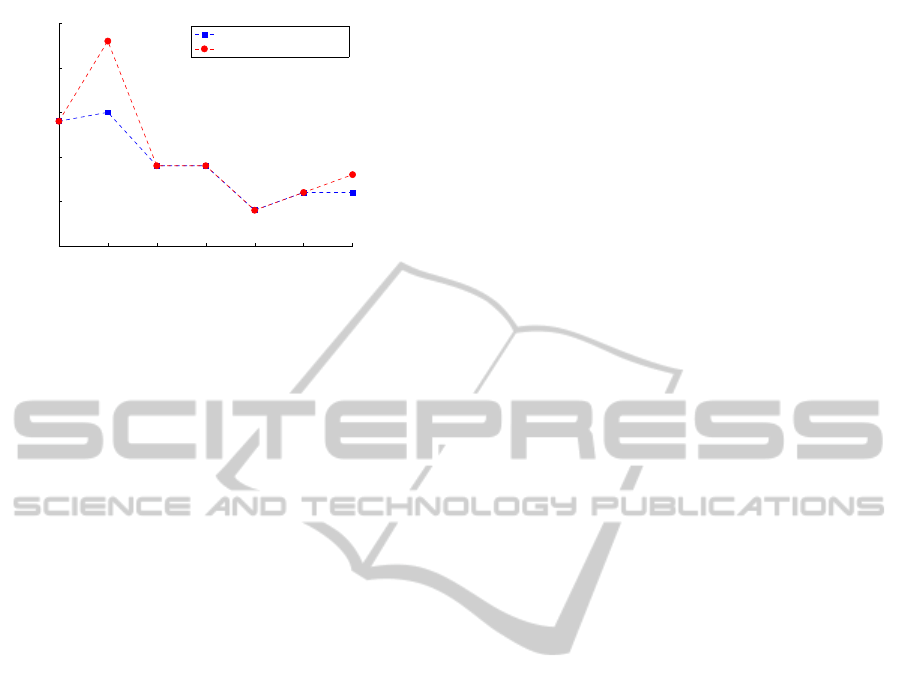
Figure 5: Plot of the mining error E of the extraction (RL-
GRADIS) and filtering steps (FRL-GRADIS) for µ = 0.5.
In case of negligible (or non-existent) inter-pattern
noise, instead, different symbols are more likely to
occur in frequent successions that cause the genera-
tion of many clusters corresponding to spurious sym-
bols, obtained from the concatenation of parts of dif-
ferent symbols. The filtering procedure overcomes
this inconvenience, as it can be seen from fig. 4 that it
is nearly not affected by the amount of inter-pattern
noise. As it is evident, the filtering procedure be-
comes fundamental for higher values of the parame-
ter η, where the clustering produces highly redundant
alphabets that would be infeasible to handle in a real-
world application. Fig. 5 shows that the mining error
after the filtering procedure remains mostly the same
for all values of η, which means that the system is
robust to the moderate alteration of the input signal.
In general, we can conclude that the system allows
for a remarkable synthesis of the extracted alphabet
despite of a modest additional mining error.
5 CONCLUSIONS
In this work we have presented a new approach to se-
quence data mining, focused on improving the inter-
pretability of the frequent patterns found in the data.
For this reason, we employed a two-steps procedure
composed of a clustering algorithm, that extracts the
frequent subsequences in a sequence database, and a
genetic algorithm that filters the returned set to re-
trieve a smaller set of patterns that best describes the
input data. For this purpose we introduced the con-
cept of coverage, that helps in recognizing the true
presence of a pattern within a sequence affected by
noise. The results show a good overall performance
and lay the foundations for further tests and improve-
ments.
REFERENCES
Agrawal, R. and Srikant, R. (1995). Mining sequential
patterns. In Data Engineering, 1995. Proceedings of
the Eleventh International Conference on, pages 3–14.
IEEE.
Bargiela, A. and Pedrycz, W. (2003). Granular computing:
an introduction. Springer.
Ji, X. and Bailey, J. (2007). An efficient technique for min-
ing approximately frequent substring patterns. In Data
mining workshops, 2007. ICDM workshops 2007.
Seventh IEEE international conference on, pages
325–330. IEEE.
Pavesi, G., Mereghetti, P., Mauri, G., and Pesole, G. (2004).
Weeder web: discovery of transcription factor binding
sites in a set of sequences from co-regulated genes.
Nucleic acids research, 32(suppl 2):W199–W203.
Rizzi, A., Del Vescovo, G., Livi, L., and Frattale Masci-
oli, F. M. (2012). A New Granular Computing Ap-
proach for Sequences Representation and Classifica-
tion. In Neural Networks (IJCNN), The 2012 Interna-
tional Joint Conference on, pages 2268–2275.
Rizzi, A., Possemato, F., Livi, L., Sebastiani, A., Giuliani,
A., and Mascioli, F. M. F. (2013). A dissimilarity-
based classifier for generalized sequences by a granu-
lar computing approach. In IJCNN, pages 1–8. IEEE.
Sinha, S. and Tompa, M. (2003). Ymf: a program for dis-
covery of novel transcription factor binding sites by
statistical overrepresentation. Nucleic acids research,
31(13):3586–3588.
Yan, X., Han, J., and Afshar, R. (2003). Clospan: Mining
closed sequential patterns in large datasets. In Pro-
ceedings of SIAM International Conference on Data
Mining, pages 166–177. SIAM.
Zaki, M. J. (2001). Spade: An efficient algorithm for
mining frequent sequences. Machine learning, 42(1-
2):31–60.
Zhu, F., Yan, X., Han, J., and Yu, P. S. (2007). Efficient dis-
covery of frequent approximate sequential patterns. In
Data Mining, 2007. ICDM 2007. Seventh IEEE Inter-
national Conference on, pages 751–756. IEEE.
InformationGranulesFilteringforInexactSequentialPatternMiningbyEvolutionaryComputation
111
