
A Novel Neural Network Computing Based Way to
Sensor and Method Fusion in Harsh Operational
Environments
Yuriy V. Shkvarko, Juan I. Yañez and Gustavo D. Martín del Campo
Department of Electrical Engineering, Center for Advanced Research and
Education of the National Polytechnic Institute, CINVESTAV-IPN, Guadalajara, Mexico
Abstract. We address a novel neural network computing-based approach to the
problem of near real-time feature enhanced fusion of remote sensing (RS) im-
agery acquired in harsh sensing environments. The novel proposition consists
in adapting the Hopfield-type maximum entropy neural network (MENN) com-
putational framework to solving the RS image fusion inverse problem. The fea-
ture enhanced fusion is performed via aggregating the descriptive experiment
design with the variational analysis (VA) inspired regularization frameworks
that lead to an adaptive procedure for proper adjustments of the MENN synap-
tic weights and bias inputs. We feature on the considerably speeded-up imple-
mentation of the MENN-based RS image fusion and verify the overall image
enhancement efficiency via computer simulations with real-world RS imagery.
1 Introduction
Relation to Prior Work–Demanding requirements of feature enhanced remote sens-
ing (RS) imaging in harsh sensing environments has spurred development of various
sensor/method fusion techniques for feature enhanced recovery of images acquired
with multimode RS systems, e.g., see [1–16] and the references therein. The crucial
problem is to reduce the fusion complexity and attain the (near) real-time processing
mode. In this study, we propose a novel approach for computationally speeded-up
enhancement of the RS imagery via adapting the Hopfield-type maximum entropy
neural network (MENN) computational framework to solving the RS image fusion
inverse problem. The feature enhanced fusion is performed via aggregating the de-
scriptive experiment design with the variational analysis (VA) inspired regularization
frameworks that lead to an adaptive procedure for proper adjustments of the MENN
synaptic weights and bias inputs. Our MENN image enhancement technique outper-
forms the recently proposed competing methods (e.g., the F-SAR-adapted anisotropic
diffusion (AD) method [13], the maximum likelihood (ML) inspired amplitude-phase
estimator (APES) [15], the robust spatial filtering (RSF) and robust adaptive spatial
filtering (RASF) procedures [16, 17], etc. that do not employ the method fusion). We
feature on the considerably speeded-up implementation of the MENN-based RS im-
age fusion and verify the overall image enhancement efficiency via computer simula-
tions with real-world RS imagery.
Shkvarko Y., Yañez J. and Martín del Campo G..
A Novel Neural Network Computing Based Way to Sensor and Method Fusion in Harsh Operational Environments.
DOI: 10.5220/0005125100190026
In Proceedings of the International Workshop on Artificial Neural Networks and Intelligent Information Processing (ANNIIP-2014), pages 19-26
ISBN: 978-989-758-041-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 Problem Model
In RS imaging, a model most often used expresses the degraded lexicographically
ordered image vector formed by a system as a sum of the noise and a linear convolu-
tion of the original scene image with the system spatial response function. The latter
is usually referred to as the point-spread function (PSF) of the RS image formation
system [1–8]. The noise vector is account to the power components in the degraded
image that correspond to system noise and environmental noise (solution-dependent
in the harsh environments due to multiplicative noise effects [8]). Let us consider for
the purpose of generality P different degraded images {g
(p)
; p = 1, …, P}
of the same
original scene image b obtained with P different RS imaging systems or methods.
The system or method fusion paradigm [11, 12] can be employed in these cases to
improve the image quality. In a system fusion context [11], we associate P different
models of the PSF with the corresponding image formation RS systems. In the meth-
od fusion context [12], we assume one given low resolution image acquisition system
but apply P different image formation algorithms to form the images {g
(p)
; p = 1, …,
P}, e.g., from the DEDR or VA families developed in the previous studies [13–17].
In the both cases, the lexicographically ordered [5, 12] K-D low resolution RS image
model is formalized by a system of P equations
g
(p)
=
()
Φ
p
b +
(p)
; p = 1,…, P (1)
with P different KK PSFs
()
Φ
p
and related K-D noise vectors {
(p)
}, respectively.
The problem of image enhancement is considered as a composite inverse problem of
restoration of the original K-D image b from P actually formed degraded K-D RS
images {g
(p)
}, given the systems' PSFs {
()
Φ
p
}. No prior knowledge about the statis-
tics of noise {
(p)
} in the data (1) is implied, thus the maximum entropy (ME) prior
model uncertainty [11, 12] conventional for harsh sensing environments is assumed.
3 ME Regularization
It is well known that the PSFs {
()
Φ
p
} are ill-conditioned for practical low/medium
resolution RS image formation systems, both passive radiometers and active ra-
dar/fractional SAR sensors [1–8]. Hence, the regularization-based approach is needed
when dealing with the feature enhanced RS image recovery problems. Next, the sta-
tistical model uncertainties about the image and noise significantly complicate the
recovery problem making inapplicable the statistically optimal Bayesian inference
techniques [5]. That is why, we adopt here the ME regularization approach [11, 12,
16, 17] in which case the desired feature enhanced RS image is to be found as a solu-
tion
ˆ
arg min
b
bbλE to the problem of minimization of the augmented objec-
tive/cost function
11
11
22
1
(|) () ( ()) ()b λ bbb
P
pp P P
p
EH J J
(2)
20

where H(b) = –
1
ln
K
kk
k
bb
is the image entropy, = (
1
, …,
P
,
P+1
)
T
is the
vector of regularization parameters, {J
p
(b) ; p = 1, …, P} compose a set of objective
(cost) functions incorporated into the optimization; here, we compose {J
p
(b); p = 1,
…, P} of equibalanced image discrepancy and image gradient map discrepancy
2
structured squared norms instead of only image discrepancy terms considered in the
previous competing studies [12–15]. Also, the second novel proposition of this study
consists in constructing J
P+1
(b) = b
T
Mb as the Tikhonov-type VA-inspired stabilizer
that controls weighted metrics properties of the image and its gradient flow map spec-
ified by the K×K matrix-form second-order pseudo differential operator M = I +
2
where I represents the discrete-form identity operator and
2
is the discrete-form
spatial Laplacian defined via a 4-nearest-neighbors differences over the x-y spatial
coordinates in the scene frame [5, 18]). The ME-regularized solution on the minimum
of (2) exists and is guaranteed to be unique because all functions that compose E(b|)
are convex. Due to the nonlinearity of the composite error function (2), the derivation
of the ME-regularized solution of the image restoration problem with system/method
fusion requires extremely complex computations with proper collaborative adjust-
ments of all “degrees of freedom” in (2) if solve this problem using the standard
gradient descent-based minimization techniques, thus yields an NP hard computation-
al problem [18, 19]. Our proposition is to solve that problem in a considerably speed-
ed-up fashion using the MENN computational framework detailed in the next section.
4 MENN for RS System/Method Fusion
The multistate Hopfield-type dynamic MENN that we propose to employ to solve the
fusion problem at hand is a P-mode expansion of the MENN developed in [11, 12]
with the K-D state vector x and K-D output vector z = sgnWx +, where W and
represent the matrix of synaptic weights and the vector of the corresponding bias
inputs of the MENN, respectively, designed to aggregate all P systems/methods to be
fused. The state values {x
k
; k = 1, …, K} of all K neurons are used to represent the
gray levels of the lexicographically ordered image vector in the process of the feature
enhancing fusion. Each neuron k receives the signals from all other neurons including
itself and a bias input. The energy function of such a neural network (NN) is ex-
pressed as [11]
TT
11
22
11 1
θ .xWx θ x
KK K
ki k i k k
ki k
EWxxx
(3)
The idea for solving the RS system/method fusion problem using the MENN is
based on the following proposition. If the energy function (3) of the NN represents
the function of a mathematical minimization problem over a parameter space, then the
state of the NN would represent the parameters and the stationary point of the net-
work would represent a local minimum of the original minimization problem
ˆ
arg min
b
bbλE
. Hence, utilizing the concept of a dynamic NN, we may translate
our image recovery problem with RS system/method fusion to the correspondent
21

problem of minimization of the energy function (3) of the related MENN. Therefore,
we define the parameters of the MENN to aggregate the corresponding parameters of
all P systems/methods to be fused adopting the equibalanced image ant its gradient
map discrepancy
2
squared norm [12] partial objective functions {J
p
(b)} in (2) that
yields
() ()
1
11
ˆ
[]
PK
pp
ki p jk ji P ki
pj
WM
, (4)
k
= –lnb
k
+
1
[
P
p
() ()
1
ˆ
K
p
p
p
jk j
j
q
] (5)
for all k, i = 1, …, K. Next, to find a minimum of the energy function (3) with speci-
fications (4), (5) the states of the network are to be updated x'' = x' + x (the super-
scripts ' and '' correspond to the state values before and after network state updating)
to provide the non-positive energy changes
2
1
2
1
( θ 1) ( ) .
K
ki i k k kk k
i
EWx xWx
(6)
due to updating of each kth neuron; k = 1, …, K. To guarantee non-positive values of
the energy changes (6) at each updating step the state update rule (z) should be as
follows, (z
): if z
k
= 0, then x
k
= 0; if z
k
> 0, then x
k
= ; if z
k
< 0, then x
k
= –
for all k = 1, …, K, where is a prescribed step-size parameter. Following the orig-
inal MENN prototype from [11, 12], we adopt = 10
–2
and the collaborative balanc-
ing method for empirical evaluation of the regularization parameters
11
1
ˆ
ˆˆ ˆ
{ ; ( ) ; , 1,..., }
P
ppp np
n
qa a r r pn P
(7)
directly from the degraded input images (1) where r
p
= trace{
() 2
()Φ
p
} represents
the pth system/method resolution factor [5], and the gain factor
ˆ
q is to be found as a
solution to the so-called resolution-to-noise balance equation (Eq. (33) from [11]).
5 Simulation Results
To analyze the performances of different RS image formation techniques, we evaluat-
ed the effectiveness of the image formation and feature enhanced recovery via per-
forming the computer simulations experiment. The test unfocused fractional SAR (F-
SAR) system image was generated via performing the matched spatial filtering
(MSF) [3, 4] of the high-resolution noised SAR 1024×1024-pixel scene image bor-
rowed from the real-world RS imagery [20] with the squared triangular PSF of 10
pixel width in the range direction (y-axis) and the truncated squared Gaussian PSF of
30 pixel width in the azimuth direction (x-axis) to be comparable with the previous
simulations formats [12, 16]. Different fusion combinations {
,
ppP} of two meth-
ods from the tested six (P = 6) specified in Table 1 were simulated and compared. For
evaluation of the enhancement/fusion performances, we employed two metrics. The
22

first one is the conventional resolution enhancement over noise suppression measure
referred to also as the signal-over-noise improvement (SNI) metric [17, 18]
() ( )
2
()
2
1
10
2
1
10log
ˆ
()
pp
kk
K
gg
k
k
fused
K
fused
kk
k
b
SNI
bb
(8)
where b
k
is the kth element of the test high-resolution image b of dimension K =
1024×1024, {
()
ˆ
p
k
b
,
(')
ˆ
p
k
b
} represent the kth elements of the tested combinations
{
,
ppP = 6} of the images fused in a particular simulation experiment, and
ˆ
{}
fused
k
b represent the corresponding pixel values of the fused image for the particular
tested combination {
,
ppP = 6}. The second one is the mean absolute error [19]
() ( )
()
10
2
1
1
10log ; , 1,...,
pp
kk
K
gg
fused
k
k
M
AE b p p P
K
(9)
The quantitative method fusion results evaluated in both metrics (8), (9) are reported
in Table 1, where subscripts
1
and
2
point at single-look and double-look F-SAR mo-
dalities: single-look (SNR = 0 dB) and double-look (SNR = 5 dB).
Table 1. SNI (8) and MAE (9) metrics corresponding to the reconstruction of the F-SAR image
with five simulated fusion combinations (the modeled system parameters are the same as in the
competing study[12]): range PSF width (at ½ from the peak value) κ
r
= 10 pixels; azimuth PSF
width (at ½ from the peak value) κ
a
= 30 pixels; Indexes 1 and 2 point at two corresponding
SNRs: SNR
1
= 0 dB (single look mode) and SNR
2
= 5 dB (double-look mode). The fusion was
performed employing the MENN technique featured in Sect. 4 for the corresponding combina-
tions of the DEDR-related techniques specified in Table 1. The dynamic MENN enhancement
and fusion results are reported for 30 performed iterations for the VA-free DEDR-related tech-
niques [11, 15] and for 8 iterations for the developed here DEDR-VA-MENN method.
Method Fusion Combination
Metric MSF
1
-MSF
2
MSF
1
-AD
2
MSF
1
-
RSF
2
MSF
1
-
RASF
2
MSF
1
-
APES
2
DEDR-
VA-MENN
SNI [dB]
7.92 8.39 8.73 9.17 9.74 10.79
MAE [dB]
20.17 19.34 17.43 15.34 13.16 12.38
In Fig. 1 we present the enhanced imaging results attained with different recovery
techniques (as specified in the figure captions). The corresponding convergence rates
for the three feasible combinations of the competing method fusion combinations are
reported in Figure 2. Such MSF
1
-AD
2
, MSF
1
-RSF
2
and DEDR-VA-MENN methods
require 30.82, 38.51 and 10.46 seconds respectively, to converge when run in a PC at
3.4 GHz with an Intel Core i7 64-bit processor and 8.00 GB of RAM. Thus, our NN
method is at least 3 times more efficient in comparison with the most competing ones.
23

(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
(j)
(k)
(l)
Fig. 1. Qualitative results of the F-SAR images enhancement without and with method fusion:
(a) original 1024×1024-pixel scene from the real-world RS imagery [20]; (b) degraded F-SAR
single look scene image; (c) AD enhancement (without fusion) [13], (d) RSF enhancement
(without fusion) [16]; (e) RASF enhancement (without fusion) [17]; (f) APES enhancement
(without fusion) [15]; (g) MSF
1
-MSF
2
fusion; (h) MSF
1
-AD
2
fusion; (i) MSF
1
-RSF
2
fusion; (j)
MSF
1
-RASF
2
fusion; (k) MSF
1
-APES
2
fusion; (l) DEDR-VA-MENN fusion. Subscripts
1
and
2
point at single-look mode (SNR
1
= 0 dB) and double-look (SNR
2
= 5 dB) F-SAR modalities.
The VA-free enhanced imaging results (e)–(k) are reported for 30 performed iterations and the
fused DEDR-VA-MENN enhancement result (l) is reported for 8 performed iterations.
24
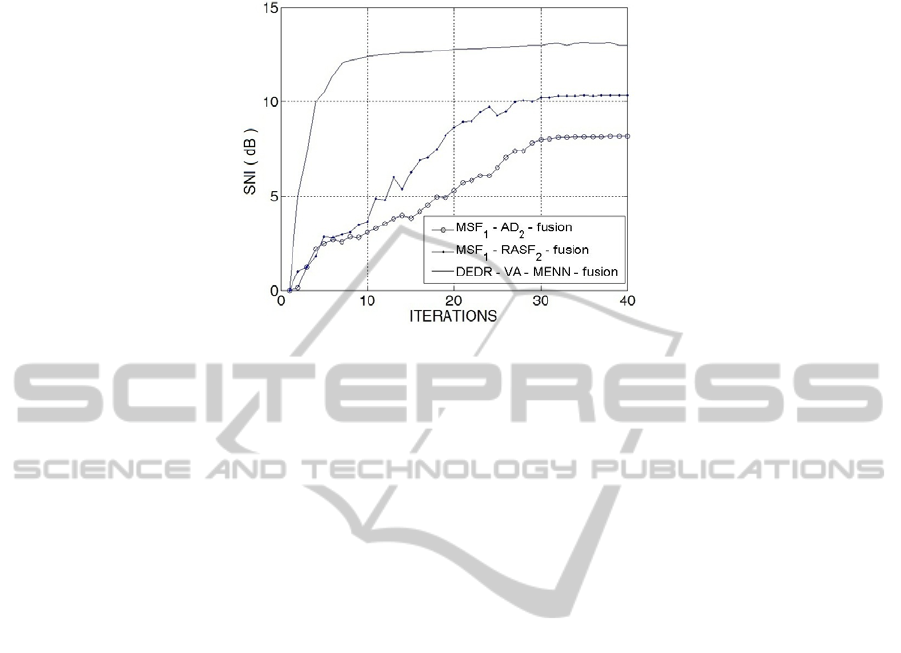
Fig. 2. Convergence rates evaluated via the SNI metric vs. number of iterations for three most
prominent DEDR-related method fusion combinations (specified in the text box) implemented
using the MENN computing technique featured in Sect. 4.
6 Conclusion
We have presented and validated via simulations a new approach for feature en-
hanced RS sensor/method fusion. In the heart of our method is adaptation of the
MENN computational framework to solving the RS image fusion inverse problems.
To achieve the feature enhanced fusion, we developed the technique for performing
the aggregation of the DEDR and VA regularization paradigms that leads to proper
adaptive adjustments of the MENN operational parameters (aggregated synaptic
weights and bias inputs). The proposed aggregated DEDR-VA-MENN enhance-
ment/fusion technique outperforms the existing low-resolution RS image formation
approaches as well as the recently proposed competing robust adaptive RS image
recovery methods that do not employ the multi-level structured regularization both in
the resolution enhancement over noise suppression and convergence rates. These
result in the speeded-up computational implementation with the considerably reduced
(near-real) processing time. The reported simulations demonstrate and verify the
feature enhanced recovery of the real-world RS imagery acquired with an F-SAR
system operating in a harsh sensing environment.
References
1. Curlander J.C., McDonough R.: Synthetic Aperture Radar––System and Signal Processing.
Wiley, NY (1991)
2. Franceschetti G., Landari R.: Synthetic Aperture Radar Processing. Wiley, NY (2005)
3. Henderson F.M. A., Lewis V., Eds.: Principles and Applications of Imaging Radar, Manual
of Remote Sensing, 3d ed., vol. 3, Willey, NY (1998)
4. Wehner D.R.: High-Resolution Radar, 2nd ed., Artech House, Boston, MA (1994)
25

5. Barrett H.H., Myers K.J.: Foundations of Image Science, Willey, NY (2004)
6. Lee J. S.: Speckle Suppression and Analysis for Synthetic Aperture Radar Images, Optical
Engineering, vol. 25, no. 5, (1986) 636-643
7. Franceschetti G., Iodice A., Perna S., Riccio D.: Efficient Simulation of Airborne SAR
Raw Data of Extended Scenes, vol. 44. No. 10. IEEE Trans. Geoscience and Remote Sens-
ing (Oct. 2006) 2851-2860
8. Ishimary A.: Wave Propagation and Scattering in Random Media. IEEE Press, NY (1997)
9. Farina A.: Antenna-Based Signal Processing Techniques for Radar Systems, Artech House,
Norwood, MA (1991)
10. Shkvarko Y.V.: Estimation of Wavefield Power Distribution in the Remotely Sensed Envi-
ronment: Bayesian Maximum Entropy Approach, vol. 50, No. 9. IEEE Trans. Signal Proc.
(Sep. 2002) 2333-2346,
11. Shkvarko Y.V., Shmaliy Y. S., Jaime-Rivas R. Torres-Cisneros M.: System Fusion in
Passive Sensing Using a Modified Hopfield Network, vol. 338. Journal of the Franklin In-
stitute (2000) 405–427
12. Shkvarko Y.V., Santos S.R., Tuxpan J.: Near Real-Time Enhancement of Fractional SAR
Imagery via Adaptive Maximum Entropy Neural Network Computing, 2012 9th European
Conference on Synthetic Aperture Radar (EUSAR’2012), ISBN: 978-3-8008-3404-7,
Nurnberg, Germany (Apr. 2012) 792-795
13. Perona P. Malik J.: Scale-Space and Edge detection Using Anisotropic Diffusion, vol. 12.
No. 7. IEEE Trans. Pattern Anal. Machine Intell. (July 1990) 629-639
14. Patel V.M., Easley G.R., Healy D.M., Chellappa R.: Compressed Synthetic Aperture Ra-
dar, vol. 4. No. 2. IEEE Journal of Selected Topics in Signal Proc. (2010) 244-254
15. Yarbidi T., J. Stoica Li, Xue P. M. Baggeroer A.B.: Source Localization and Sensing: A
Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares, vol. 46,
No. 1. IEEE Trans. Aerospace and Electronic Syst. (2010) 425-443
16. Shkvarko Y.V., Tuxpan J., Santos S.R.: Dynamic Experiment Design Regularization Ap-
proach to Adaptive Imaging with Array Radar/SAR Sensor Systems, Sensors, no 5, (2011)
4483-4511
17. Shkvarko Y.V., Tuxpan J., Santos S.R.: High-Resolution Imaging with Uncertain Radar
Measurement Data: A Doubly Regularized Compressive Sensing Experiment Design Ap-
proach, in Proc. IEEE 2012 IGARS Symposium, ISBN: 978-1-467311-51/12, Munich,
Germany (July 2012) 6976-6970
18. Mathews J.H.: Numerical Methods for Mathematics, Science, and Engineering, Second
Edition, Prentice Hall, Englewood Cliffs, NJ (1992)
19. Ponomaryov V., Rosales A., Gallegos F., Loboda I.: Adaptive Vector Directional filters to
Process Multichannel Images, vol. E90-B, No. 2. IEICE Trans. Communications (Feb.
2007) 429–430
20. TERRAX-SAR Images, Available at: http://www.astrium-geo.com/en/19-galery?img=1690
&search=gallery&type=0&sensor=26&resolution=0&continent=0&application=0&theme=0
26
