New Learning Rules for Three-layered Feed-forward

Neural Networks based on a General Learning Schema

Christina Klüver

and Jürgen Klüver

Department of Computer Science and Business Information Systems,

University of Duisburg-Essen, Essen, Germany

COBASC-Research Group, Department of Computer Science and Business Information

Systems, University of Duisburg-Essen, Essen, Germany

Abstract. We propose a general schema for learning rules in neural networks,

the General Enforcing Rule Schema (GERS), from which we infer new

simplified learning rules for in particular supervised learning of three-layered

feed-forward networks, namely Enforcing Rule Supervised ERS and ERS2.

These rules are comparatively simpler than the established rule of

Backpropagation and their performance is at least equivalent. The new rules are

compared with Backpropagation in different experiments; an additional

comparison is performed with real data for the prediction of parcel delivering.

1 Introduction

Most of the established learning rules for neural networks are, as is well known,

“Hebbian” ones, i.e. they are based on the principle of Hebb that learning is the

changing of connections between the (artificial) neurons. Although Hebb speaks of

the changing of “cells” rather than of connections [1] it seems safe to transfer his

principle to the changing of connections. In this sense Hebb may be called the

(unintentional) father of learning neural networks.

The Hebbian learning rules and their numerous variants have been applied for a

long time and they have frequently demonstrated their usefulness. Yet despite their

obvious success they have a slight methodical and theoretical blemish:

From a methodical point of view it seems a bit strange that the activation values or

output values of the neurons respectively are used on the one hand as cause variables

and on the other as performance variables. Consider, e.g., a standard version of the

Backpropagation rule, which we shall use also for comparison reasons:





net



 o



, if j is an output neuron

net







, if j is a neuron from the hidden layer













(1)

Here the activation or output value respectively of the neuron j represents as a part

of the learning rule a cause variable or an independent variable respectively. On the

other hand the performance of the network as a result of the application of the

learning rule is measured by the output values and that means the activation values of

the different output neurons. Hence the activation values are also used as performance

Klüver C. and Klüver J..

New Learning Rules for Three-layered Feed-forward Neural Networks based on a General Learning Schema.

DOI: 10.5220/0005125600270036

In Proceedings of the International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing (ANNIIP-2014), pages 27-36

ISBN: 978-989-758-041-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

variables or dependent variables.

To be sure, this double usage of the activation values is no logical circle. Yet it

seems rather redundant to use the activation values twofold. Hence it would be

desirable to construct learning rules where the activation or output values are used

only as performance variables. Mathematically the rules would become simpler,

which would be an advantage for teaching, programming, and application purposes.

In addition, from a theoretical point of view it is rather unsatisfactory that the

specific learning rules for different types of learning, particularly supervised learning

and self-organized learning, have not much in common, besides the general aspects of

Hebb’s principle. The Backpropagation rule as a paradigm for supervised learning for

example has on a first and second sight not much to do with the well-known “Winner-

takes all” rule that is used in Kohonen Feature Maps for self-organized learning.

Hence it would be desirable to construct a general learning schema that would be the

basis for learning rules, applied to different types of learning, and that is also based on

Hebb’s proven principle - in neuroinformatics and biology (cf. e.g. [6]).

In a formal sense its essence certainly is the increasing or decreasing respectively

of the weight values between sending neurons and a receiving artificial neuron, as

many learning rules take into account. By leaving out the output values of the

respective neurons we obtain a general learning schema in its simplest form as

w

=  c and 0  c  1.

(2)

The constant c has the same function as the learning rate  in different standard

learning rules. If one uses for example the linear activation function

 w



(3)

then in large networks the activation values frequently become too large. In order to

avoid such an increasing equation (2) can be extended by introducing a “dampening

factor”. Then the schema becomes

w

=  c * (1 – w

(t) 

(4)

if w

(t) is the according weight value at time t, i.e. before changing. The dampening

factor is used in order to keep the weight values in the interval (-1, 1).

Equations (2) and (4) are just schemas, namely the General Enforcing Rule

Schemas (GERS). The application to different types of learning needs in the two

types investigated by us, namely supervised learning and self-organized learning,

additional components. We chose these types of learning because they are by far the

most important ones in the usage of neural networks. By the way, when dealing with

reinforcement learning equation (4) can be used directly as the according learning

rule.

For example, an according learning rule for self-organized learning, which we

developed for a self-organized learning network (Self Enforcing Network, SEN), is

w(t+1) = w(t) + w and

w = c

(5)

c is again a learning rate and v

is the according value in a so-called semantical

matrix, i.e. the data base for the learning process (cf. [2]; [3]). Obviously this is a

direct application of GERS to this type of learning without taking into regard the

output values. The main emphasis in this article, however, is put on the application of

GERS to supervised learning, in particular learning of three-layered feed-forward

networks.

2 ERS – Enforcing Rule Supervised

Three-layered networks need as learning rules strictly speaking two components,

namely the variation of the weights between the hidden and the output layer and the

variation of the weights between the input layer and the hidden one. The first

component of our new rule is computed by

∆w

c∗1‐w





∗ δ

j

∗sgn





(6)



is of course the distance between the output neuron j and the respective component

in the target vector, i.e. 

= t

– o

. Note that the factor sgn(o

) is used only as the sign

of the whole product; the absolute numerical value of o

does not matter. For brevity’s

sake we call this rule ERS – Enforcing Rule Supervised. The second component of

ERS is:





 o

, if j is output neuron





, else











(7)

For experimental and methodical purposes we also constructed a variant of ERS by

adding the factor o

∆w

c∗ 1‐w





∗ δ

j

∗o

(8)

This variant is more similar to the established rules because of the factor o

; for the

sake of brevity we call this variant ERS2. The computation of the weight variation

between the hidden and the output layer is the same as in equation (6).

Because we wished to compare ERS with standard learning rules we performed our

experiments also with a standard version of the Backpropagation Rule (BP), already

shown in equation (1).

There are numerous other versions of BP but we used the

standard version usually introduced in textbooks on neural networks (e.g. [5]).

Equation (7) shows that ERS and ERS2 are also “back propagating” rules as they

propagate the error to the weight values between input and hidden layer. Recently a

learning rule for multilayered feed forward networks has been proposed, namely a so-

called “No-Prop” algorithm, which just uses the Delta rule for the variation of the

weight values between output and hidden layer and leaves the other weight values

fixed [8]. As far as we know this algorithm has been analyzed just for a few

examples.

3 Experimental Design and Results

We analyzed the performance of ERS and ERS2 in comparison to BP with networks

Attempts to improve standard BP can be found, e.g., in Orr and Müller[4].

of different size and different topologies.

The input and target values are generated at

random from the interval between 0.00 and 1.00. The initial weight values of the

networks are also generated at random from the interval (-0.5, 0.5) or (-1, 1). A

learning process is considered as successful if 0    0.01. If such a value is not

reached after mainly 2.000 learning steps the learning run stops and is marked as

unsuccessful. In each single experiment ERS, ERS2, and BP got the same initial

matrix and the same input and target patterns. The learning rate c for ERS and ERS 2

was in the first series c = 0.2 and 0.4 respectively; when enlarging the networks we

decreased the learning rate to c = 0.04. In all experiments in the case of BP was

 =

0.9. For error computation we used the Euclidean distance.

The activation function is tangent hyperbolicus tanh(x) for ERS and ERS2; for BP

we used the logistic function. To simplify the experiments we chose the same size of

the patterns as the number of patterns to be learned, i.e. if the networks had for

example to learn 20 patterns the patterns consisted of 20 components. When we speak

of “pattern” we mean strictly speaking a pair of patterns, namely an input pattern and

a target pattern.

The first experimental series was performed with 10 different patterns for each

network, generated at random. In all 1000 different tests were performed and the

maximal iteration number, i.e. number of learning steps, was limited to 2.000. Table 1

shows the results for the most suited topologies respectively for all learning rules; the

topologies are obtained from according experiments. The values given for the mean

refer to all experiments and only to successfully learned patterns; SD (standard

deviation) was computed for all experiments, i.e. also the unsuccessful ones. LR is the

learning rate and AF the respective activation function. Min / Max refers to minimal

or maximal learning steps respectively.

Table 1. Performance for “ideal” topologies; the numbers in the first line represent the numbers

of successful learning processes.

Learning Rule

Topology

Weight intervals

10—25—10

(-1.0 , 1.0)

ERS

10—65—10

(-1.0 , +1.0)

ERS2

10—40—10

(-0.5 , 0.5)

Performance

LR /AF

Min / Max

Ø / SD

998

0.9 / logistic

38 / 1015

112 / 98

1000

0.1 / TanH

110 / 1282

241 / 85

1000

0.4 / TanH

47 / 1419

134 / 80

The next step was to test the performance of the learning rules with different

topologies and different intervals of the generated weight values. Table 2 shows the

results.

According to our experiments ERS and ERS2 need in general a larger number of

neurons in the hidden layer to reach better results than the BP networks. It might be

not by chance that Widrow et al. (loc. cit.) report the same result when comparing

their algorithm to BP.

Viktor Schäfer has implemented the Tool, which enables the comparison between the rules.

Table 2. Learning performance with 10 patterns and the same topologies.

Topology

Weight intervals

—30—10

(-0.5 , 0.5)

10—40—10

(-0.5 , 0.5)

10—50—10

(-0.3 , 0.3)

LR /AF

Min / Max

Ø / SD

952

0.9 / logistic

304 / 4787

885 / 622

939

0.9 / logistic

290 / 6809

866 / 639

962

0.9 / logistic

208 / 4769

684 / 496

ERS

LR /AF

Min / Max

Ø / SD

934

0.2 / TanH

53 / 4746

310 / 468

982

0.2 / TanH

61 / 5857

205 / 240

998

0.2 / TanH

147 / 9255

778 / 857

ERS2

LR /AF

Min / Max

Ø / SD

998

0.4 / TanH

36 / 2798

140 / 160

1000

0.4 / TanH

38 / 660

127 / 71

989

0.4 / TanH

98 / 9942

625 / 1093

For the following experiments, we decided to make a compromise with respect to

the number of neurons in the hidden layer, i.e. the acceptable according number for

each learning rule, as a result of several samples.

The next figure shows the results for the learning processes with 20, 30, and 50

patterns. The two chief results are:

a) The speed, i.e. the number of learning steps, is approximately the same with all

learning rules. In some experiments BP was the fastest learning rule, in others ERS

and ERS2. Yet the differences are not significant in the sense that there is a general

trend, which rule is the best one.

b) In all experiments ERS and ERS2 are more reliable than BP, i.e. their number of

successfully completed learning processes is always larger than that of BP. Hence,

although the new learning rules ERS and ERS2 are not significantly faster than BP

they are obviously more reliable – an interesting result in particular for practical

applications of neural networks (see below the real data experiments).

Fig. 1. Learning performance with 20, 30, and 50 patterns.

Details can be seen in the following table:

Table 3. Learning performance: details.

Topology

Weight intervals

—60—20

(-0.5 , 0.5)

30—80—30

(-1.0 , 1.0)

50—100—50

(-1.0 , 1.0)

LR /AF

Min / Max

Ø / SD

980

0.9 / logistic

344 / 4527

849.5 / 578.5

992

0.9 / logistic

337 / 3222

614 / 339

992

0.9 / logistic

467 / 3529

802 / 321

ERS

LR /AF

Min / Max

Ø / SD

1000

0.2 / TanH

251 / 6068

780 / 494.5

995

0.1 / TanH

230 / 3878

556.5 / 201

1000

0.03 / TanH

351 / 4114

978 / 492.5

ERS2

LR /AF

Min / Max

Ø / SD

998

0.3 / TanH

254 / 9970

1969.5 / 1414

998

0.2 / TanH

460/ 4468

1296.5 / 935

1000

0.04 / TanH

361 / 3274

666 / 287

For comparison purposes we repeated all experiments with an error rate of 0.000

for each pattern number and each topology. ERS and ERS2 were successful but only

with approximately twice iterations than in the previous experiments. The used

standard version of BP did not succeed at all, i.e. it only seldom reached the learning

goal. Additional parameters like momentum or decay would probably have been

necessary; it will be interesting if such parameters can also improve the performance

of ERS and ERS2.

4 A Case Study: Predictions of Parcel Delivering Times

A severe problem for all delivery services is to inform their customers about the

probable time the parcels and other products will be delivered to the customers. In

cooperation with DHL, the delivery service of the Deutsche Post, one of the biggest

logistic firms worldwide, we obtained real delivery data for several districts of Essen,

a large city in the West of Germany. The districts consist altogether of 20 streets. As

far as we know we were the first to attempt predictions with neural networks for the

problem of prognosticating different time intervals or time windows.

Our research question was two-fold, namely on the one hand to analyze if

successful predictions for delivery times in different streets are possible at all and on

the other hand which one of the three learning rules, compared in the experiments

above, reached the best prediction results.

In all three cases we used the same network topology, namely 34

—45—34. The

number of input and output neurons is due to the number of time intervals each day

was divided into. Hence each input and output neuron represents a certain time

interval. The training phase was 20 weeks; each day in a week was mapped to the

according day in in the next week. Hence we obtained for each day in a week a time

series of twenty components. For BP we used again the logistic function and a

learning rate of 0.9; for ERS we used a so-called logarithmic-linear function that was

newly developed by us (cf. [2]):











1



∗w



 , A



0







1

∗w





0





(9)

The learning rate was 0.04; ERS2 had the tanh-function and a learning rate of 0.08.

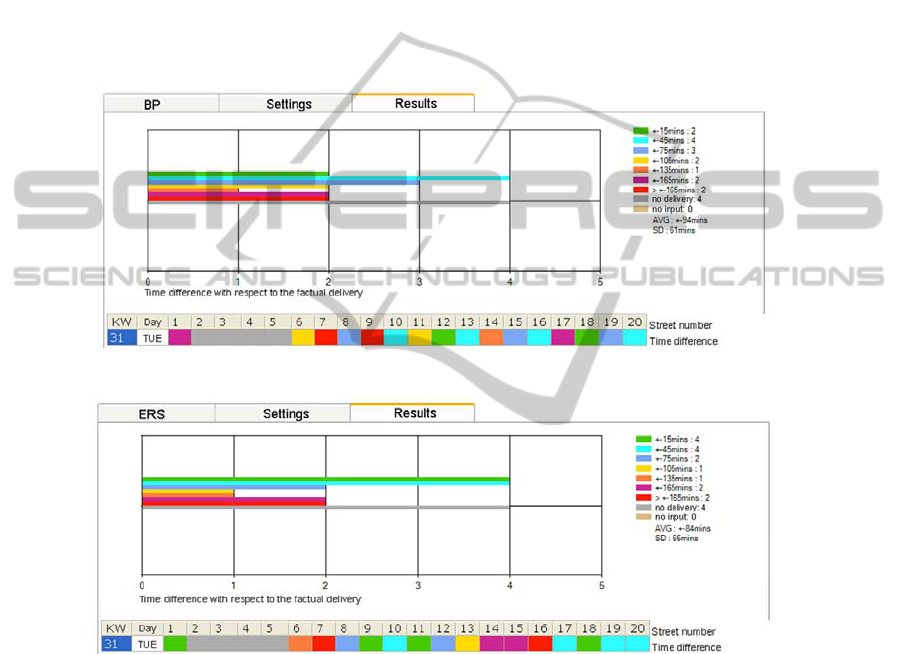
The following figure shows the performance of BP for Tuesday in week 31 (KW);

the numbers below the figure show how many predictions are characterized by a

specific time difference with respect to the factual delivery. For example, 2

predictions differed just  15 minutes from the factual time (top row), 4 predictions

differed  45 minutes (second row) and so on. The number of predictions is the

according mean of the 20 streets.

The next 2 figures show the performances of ERS and ERS2 for the same day:

Fig. 2. Prediction performance of BP for Tuesday.

Fig. 3. Prediction performance of ERS.

An additional remark is necessary: The figures show just the results for 16 time

intervals. This due to the fact that frequently no parcels were delivered at all; hence it

would be quite useless to compute a difference for such days between the predicted

time and the factually non-existent time. Therefore the prediction list is an adjusted

one, which is certainly not the fault of the different networks.

The results for the other days are nearly the same as those for Tuesday; the shown

results are in this way representative.

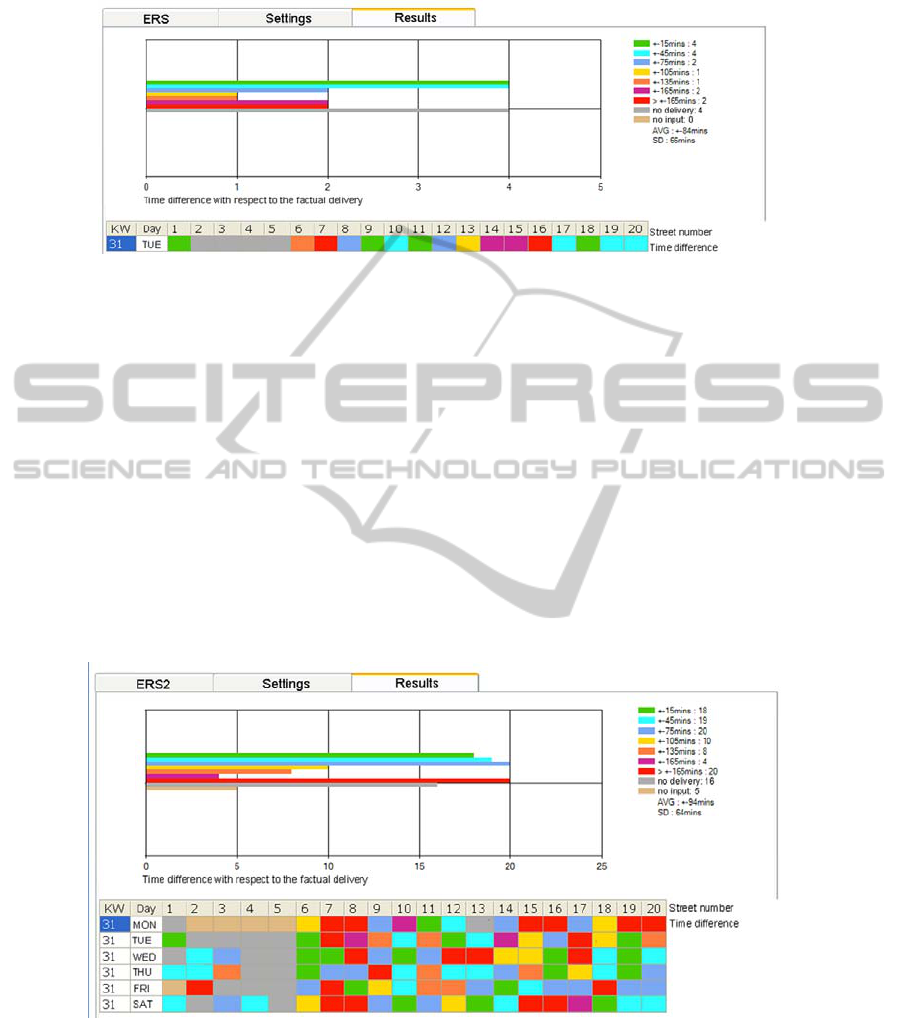
Fig. 4. Prediction performance of ERS2.

With respect to the first questions if such predictions are possible at all, the answer

is “to a certain degree”. The delivery experts at DHL commented on our results that

indeed delivery times permanently vary because of the changing of drivers, choosing

different routes by the drivers, possibility of traffic jams and road works, differences

between customers who frequently and those who only seldom receive parcels, and

other factors. The opinion of the experts in general was that our results could probably

still be improved but that these results are significantly better than their own

estimates. Hence further cooperation will be arranged.

The answer to the second question generally confirms the results of the

experiments described above. All three learning rules perform with a comparable

success. BP and ERS2 are rather similar in their prediction successes; ERS is more

successful, i.e. it generated slightly more very good predictions. Hence this case study

is another indicator that at least ERS is a bit more reliable than BP.

Finally we show in addition the mean of the performance values for all streets and

all days of the week that should be predicted. Fig. 5 contains the results of ERS:

Fig. 5. Mean values of ERS in detail.

The next table shows the results for all learning rules:

Table 4. Comparison of the mean values of the different rules.

Time

difference:

±15 ±45 ±75 ±105 ±135 ±165 >±165

delivery

input

AVG SD

BP 16 16 25 11 9 6 16 16 5 ± 94 60

ERS 18 19 20 10 8 4 20 16 5 ± 94 64

ERS2 20 17 19 9 9 5 20 16 5 ± 95 65

These results show that the trend demonstrated for Tuesday is indeed

representative. The DHL experts again assured us that they were not able to produce

comparable results.

5 CONCLUSION

To sum up, both ERS versions performed at least as well as BP. The general trend in

all experiments and in the case study is unambiguous: ERS and ERS2 seem to be

quite suited to solve complex learning problems at least as well as the established

learning rule, namely BP. The main differences between the rules are on the one hand

that ERS and ERS2 operate well with a small learning rate, which should be even

decreased if the networks become larger. BP in contrast always needs a rather large

learning rate. One has to take into account, though, that frequently the size of the

learning rate depends on the selection of the activation function (e.g. [7]). In our

experiments ERS and ERS2 performed best with tanh and BP with the logistic

function; in the case study we chose the new logarithmic-linear function for ERS,

which performed rather well, and which we already had successfully applied in our

new self-organized learning network [2, 3].

On the other hand both ERS versions perform best with rather large hidden layers;

BP in contrast usually needs only smaller ones. It is probably not by chance that

Widrow [8] (loc. cit.), as remarked, report a similar result from their experiments with

the No-Prop algorithm and BP; further investigations will possibly explain this

remarkable concordance.

Of course several methodical caveats must be taken into consideration. These

results confirm that ERS and ERS2 are able to solve different learning tasks as far as

we have them analyzed. Yet the results are from samples with certain topologies and

from a specific real data case study and they cannot claim to be representative in the

sense that, e.g., ERS and ERS2 are always as fast as BP or for each problem more

reliable than BP. After all, BP has been tested in its different versions for more than

two decades and with the two versions of ERS we are just in the beginning. Other

parameters like other activation functions, different topologies, e.g. short cuts, more

levels, introduction of momentum and decay, or other versions of BP should be

investigated too, which we shall undertake in the near future. In addition, the

influence of parameters like momentum on the two ERS rules should and will be

analyzed too.

It might well be, by the way, that there are classes of learning problems where BP

is significantly better than ERS or ERS2, but it might also be that there are other

problem classes where ERS or ERS2 should be preferred. Without doubt ERS and

ERS2 are comparatively simpler than BP and hence also simpler to program; in

particular ERS and ERS2 do not need any external parameters like, e.g., momentum.

According to our didactical experiences BP is usually rather difficult for students of

computer science to understand. Teaching ERS and ERS2 as an alternative to BP will

be an interesting didactical experience; Widrow [8] stress for the same reasons the

comparative simplicity of the No-Prop algorithm as an advantage with respect to BP.

To emphasize it again, we do not mean that BP or the Delta rule become obsolete

because of our new learning rules. These established learning rules have been

analyzed and applied for many years and they will be always useful and necessary

algorithms. ERS and ERS2 for three-layered or more-layered feed forward networks

might be additional useful tools for users of neural networks – not more but also not

less.

References

1. Hebb, D.O.: The Organization of Behavior. Wiley, New York (1949)

2. Klüver, C., Klüver, J.: Self-organized Learning by Self-Enforcing Networks. In: Rojas I,

Joya G, Cabestany J (eds.): IWANN 2013, Part I, Lecture Notes in Computer Science Vol.

7902, Springer, Berlin Heidelberg (2013) 518–529

3. Klüver, C., Klüver, J.: OSWI: A consulting system for pupils and prospective students on

the basis of neural networks. In: AI & Society. Springer-Verlag, London (2014) DOI

10.1007/s00146-014-0542-y

4. Orr, G., Müller, K.: Neural Networks: Tricks of the Trade, Springer, Berlin Heidelberg

New York (1998)

5. Patterson, D.: Artificial Neural Networks, Theory and Applications. Prentice Hall, New

Jersey (1996)

6. Seung, S.: Connectome. Houghton Mifflin Harcourt, Boston New York (2012)

7. Thimm, G., Fiesler, E.: Optimal Setting of Weights, Learning Rate, and Gain. IDIAP-

Research Report 04-1997 http://publications.idiap.ch/downloads/reports/1997/rr97-04.pdf

(1997)

8. Widrow, B., Greenblatt, A., Kim, Y., Park, D.: 2013. The No-Prop algorithm: A new

learning algorithm for multilayer neural networks. Neural Networks 37. Elsevier Science

Ltd, Oxford (2013) 182–188