An Ordering Procedure for Admissible Network Conﬁgurations to

Regularize DFR Optimization Problems in Smart Grids

A. Rizzi, F. Possemato, S. Caschera, M. Paschero and F. M. Frattale Mascioli

Dipartimento di Ingegneria dell’Informazione, Elettronica e Telecomunicazioni (DIET)

SAPIENZA University of Rome, Via Eudossiana 18, 00184, Rome, Italy

Keywords:

Distribution Feeder Reconﬁguration, Power Factor Correction, Power Losses Minimization, Smart Grid,

Graph Theory, Optimization, Genetic Algorithm.

Abstract:

The power loss reduction is one of the main targets for any electrical energy distribution company. In this paper

the problem of the joint optimization of both topology and network parameters in a real Smart Grid is faced.

A portion of the Italian electric distribution network managed by the ACEA Distribuzione S.p.A. located in

Rome is considered. It includes about 1200 user loads, 70 km of Medium Voltage (MV) lines, 6 feeders,

a Thyristor Voltage Regulator (TVR) and 6 distributed energy sources (5 generator sets and 1 photovoltaic

plant). The power factor correction (PFC) is performed tuning the 5 generator sets and setting the state of the

breakers in order to perform the distributed feeder reconﬁguration (DFR). The joint PFC and DFR problem

is faced by considering a suited objective function and by adopting a genetic algorithm. In this paper we

present a heuristic method to compare the graphs of two admissible topologies, such that similar graphs are

characterized by close active power loss values. This criterion is used to deﬁne a suited ordering of the list

of admissible conﬁgurations, aiming to improve the continuity of the ﬁtness function to the variation of the

conﬁgurations parameter. Testsareperformed by feeding the simulation environment with real data concerning

dissipated and generated active and reactive power values. Preliminary results are very interesting, showing

that, for the considered real network, the proposed ordering criteria for admissible network conﬁgurations can

facilitate the optimization process.

1 INTRODUCTION

The wide diffusion of Distributed Generation (DG)

represents a possible development of modern electri-

cal distribution systems that can evolve towards Smart

Grids (SG). It can be stated that a SG is a new gen-

eration electrical network where smartness, dynam-

icity, safety and reliability are achieved through the

use of Information and Communication Technologies

(ICT) (Dahu, 2011). Recently, electrical distribution

networks have grown quickly and the backbones of

the existing infrastructures have been built when DG

was not considered at all. As a consequence, elec-

tric power is distributed to the ﬁnal user through a

unidirectional transportation infrastructure. This con-

ﬁguration implies a considerable transportation con-

sumption due to the long distance between producers

and consumers. The main problems concerning actual

networks are listed below:

• losses due to long distance between producers and

users

• management of energetic ﬂows

• inefﬁcient use of DG related to renewable energy

generators

• lag in the reaction time in case of blackout

• incomplete and inaccurate knowledge on the in-

stantaneous status of the infrastructure

In order to overcome these drawbacks, a large number

of sensors must be installed on the network to obtain

a complete information on the instantaneous status of

the infrastructure. This information can be used as

input of an optimization control algorithm capable of

determining in real time the best network conﬁgura-

tion able to satisfy the instantaneous power request

and to drive suitable actuators, optimizing a given ob-

jective function.

The number of DG units in electrical distribution

networks has been increasing very fast in the last few

years (Singh et al., 2011). Technologies used for DG

applications could include non-renewable energy re-

sources, such as internal combustion engines, com-

273

Rizzi A., Possemato F., Caschera S., Paschero M. and Frattale Mascioli F..

An Ordering Procedure for Admissible Network Conﬁgurations to Regularize DFR Optimization Problems in Smart Grids.

DOI: 10.5220/0005127302730280

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 273-280

ISBN: 978-989-758-052-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

bined cycles, combustion turbines as well as micro-

turbines and renewable energy resources, for example

photovoltaic and wind turbines.

Another important degree of freedom that can be

used to minimize active power loss in distribution

feeders is offered by the opportunity to perform the

distribution feeders reconﬁguration (DFR). This oper-

ation consists in switching a certain number of break-

ers, altering the topological structure of the network

considering the topological contraints. Therefore, the

DFR problem can be conceptualized as the task of

choosing the status of network breakers resulting in

the conﬁguration with minimal power losses, while

all the system constraints are satisﬁed. The main

drawback of DFR is that it results in a complex non-

linear combinatorial problem, since the status of the

switches is non-differentiable. This discontinuous be-

haviour makes the optimization problem related to

DFR very hard to solve. In recent years, many re-

searchers have proposed interesting solutions. Prob-

ably the ﬁrst contribution in this direction can be

found in (Merlin and Back, 1975), where a branch and

bound type optimization technique is used in order to

ﬁnd the minimal loss operating conﬁguration, for the

distribution system, at a speciﬁc load condition. Af-

ter this work, a few different techniques are proposed

by many researchers (Civanlar et al., 1988), (Carreno

et al., 2008). In recent years, new heuristic algorithms

are proposed in the literature with good results. Prob-

ably, the ﬁrst attempt to use genetic algorithms (GAs)

to solve the DFR problem with minimal losses can be

found in (Nara et al., 1992). Since then, a great num-

ber of publications based on evolutionary algorithms

are proposed in the literature (Storti et al., 2013a),

(Possemato et al., 2013). Recently, GA is also used

to solve the DFR problem with DG (Chandramohan

et al., 2010), (Storti et al., 2013b). One of the main

difﬁculties for solving the DFR problem using evolu-

tionary algorithms is the radiality constraint. A solu-

tion to this problem is proposed in (Storti et al., 2014)

where a cooperation with ACEA Distribuzione S.p.A.

is engaged with the aim to design a control strategy

for the SG under development in the west area of

Rome. The authors conclude that the DFR is a chal-

lenging problem do to high non linearity of the objec-

tive function. For this reason, in this paper we propose

an heuristic method based on the Hamming distance

between network conﬁgurations, to improve the regu-

larity of the objective function. The rest of the paper

is organized as follows: in section 2 we present the

main characteristics of the SG under analysis, in sec-

tion 3 we formulate the DFR optimization problem,

then in section 4 we describe an ordering criteria for

the network conﬁgurations. Finally, in section 5 we

report the results obtained by applying the proposed

ordering heuristic to the set of admissible conﬁgura-

tions together with a GA. Moreover, we compare re-

sults of the genetic optimization of network topology

and DGs parameters for the ACEA SG, in the cases

of unordered (Storti et al., 2014) and ordered conﬁg-

urations.

2 NETWORK SPECIFICATIONS

The portion of the network we consider in this paper

is located in the west area of Rome. The entire SG is

made up of:

• 5 feeders at 20 kV

• 1 feeder at 8.4 kV

• 2 High Voltage (HV) substations

• 76 Medium Voltage (MV) substations

• 5 generator sets (DGs)

• 1 photovoltaic generator (DG)

• 1 thyristor voltage regulator (TVR)

• 106 three-phase breakers

• 70 km of cables

• 1200 user loads

In each HV substation there is a transformer with 150

kV at the primary winding and 20 kV at the secondary

winding (HV/MV transformer). The cables, the pho-

tovoltaic plant, the MV substations and the TVR are

located in the MV portion of the network, whereas the

user loads and the 5 generator sets are located in the

LV portion of the network.

The TVR is a series voltage compensation device.

It performs a bi-directional voltage regulation that

maintains the system voltage within speciﬁed ranges.

The bi-directional relation between the input and the

output voltage is deﬁned as follows:

out

= V

+ N

tap

∆V N

tap

∈ {0, ±1,±2,±3} (1)

where the values of V

and V

out

are expressed in kV

and the ∆V is 0.1 kV. The voltage rated value of V

is 8.4 kV. Each MV substation is equipped with 2

breakers (switches) that allow it to connect with the

network in different ways. By changing the state of

these switches it is possible to modify the topology of

the network.

3 PROBLEM FORMULATION

In this paper, we consider the joint PFC and DFR

problem for minimum active power losses, satisfying

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

274

constraints on nodes voltage and branches current as

well as system operating constraints.

3.1 Optimization Procedure

In this section we formulate the problem of active

power losses minimization in SGs. It consists in

ﬁnding the optimal network parameters and topolog-

ical conﬁguration that minimize the value of the total

active power losses in the network, considering the

constraints imposed on voltages and currents due to

safety or quality of service issues. Consider an admis-

sible set E of the network parameters and a suitable

cost function J : E → R that associates a real number

to each element in E. Formally, the problem consists

in minimizing the function J in E. Mathematically we

can express the cost function J as follows:

J(k) =

loss

(k)

gen

(k)

gen

(k) − P

load

gen

(k)

(2)

where k represents an instance of the network pa-

rameters, P

gen

(k) is the total power generated by all

sources, P

load

is the total power absorbed by the loads,

and their difference P

loss

(k) represents the total losses

in the network. Let’s consider a generic SG character-

ized by n real parameters, m integer parameters and p

nominal parameters. We can express the domain of

the ordinal parameters as:

′



′

∈ R

× Z

: k

′

min

≤ k

′

≤ k

′

max



(3)

in which k

′

min

and k

′

max

represent the vectors of the

minimum and maximum values of the network ordi-

nal parameters k

′

. Concerning the nominal parame-

ters, k

′′

, the domain is a set A

′′

of all possible admis-

sible elements for such parameters:

′′



′′

∈ X

× · ··× X



(4)

in which X

is a generic nominal set with i = 1,..., p.

The overall domain A is deﬁned as A = A

′

× A

′′

and

the parameters vector k is an element of such domain.

Without loss of generality, we consider as possible

to measure the voltages and the currents at all loca-

tions in the network. In order to be valid, a solution k

must satisfy the constraints on voltages and currents

deﬁned below:

B =



k ∈ R

× Z

× X

× · ··× X

min

≤ V

(k) ≤ V

max

,i = 1,..,M



C =



k ∈ R

× Z

× X

× · ··× X

(k)| ≤ I

max

,i = 1,..,R



where V

(k) is the voltage magnitude of node i for a

ﬁxed instance of parameters k, M represents the num-

ber of nodes, V

min

, V

max

are the voltage limits for

node i, while |I

(k)| represents the current magnitude

of branch i for a particular instance of parameters k, R

the number of branches and I

max

the current limit for

branch i. The deﬁnitions given above allow to deﬁne

the admissible set E as follows:

E = A ∩ B ∩C (5)

This formulation is an example of mixed-integer

black box-based optimization problem because the

optimization variables are integer and real. Moreover,

it is not practically possible to derive expression (2) in

closed form as a function of k; for this reason we em-

ploy a GA (derivative free approach) as optimization

algorithm. The constrained optimization problem is

faced by deﬁning the objective function as a convex

combination of two competitive terms:

F(k) = αJ(k) + (1− α)Γ(k) (6)

where α is a real number in the range [0, 1] used to ad-

just the relative weight of the power losses term J(k)

over the constraints term Γ(k). The function Γ(k) is

deﬁned as follows:

Γ(k) = (1− β)Γ

(k) + βΓ

(k) (7)

in which β is a real number in the range [0, 1] used

to adjust the relative weight of the violation of current

constraints Γ

(k) with respect to the term related to

voltages violation Γ

(k). In this paper it is performed

the minimization of F(k) in A. Further details of the

optimization procedure can be found in (Storti et al.,

2013a).

3.2 Admissible Network Conﬁgurations

In order to perform the optimization procedure de-

scribed in section 3.1, we introduce a suitable repre-

sentation of the SG as a non oriented graph GhN,Ei,

in which N and E are the nodes and the edges of the

real network, respectively. Let’s deﬁne as

Ei,

the reduced graph of the network. The objective

of this representation is to properly describe all the

possible system reconﬁgurations satisfying the topol-

ogy constraints. The reduced graph of the network

Ei doesn’t contain all the information of the

original network graph GhN,Ei because for our pur-

poses we need only to know how different portions

of the network can be electrically connected. As de-

scribed in (Storti et al., 2014), the mapping of the real

network in the simpliﬁed graph version is performed

through two main steps:

• The nodes

N of the simpliﬁed graph are used to

model 2 different types of original nodes N. The

ﬁrst one represents nodes at 150kV providing the

energy balance of the active and reactive power

AnOrderingProcedureforAdmissibleNetworkConfigurationstoRegularizeDFROptimizationProblemsinSmartGrids

275

in the SG. In following sections we will refer to

it as HV node. The second one can represent a

single MV real substation eventually connected to

loads, DGs and TVR, or a set of MV substations,

MV). In both cases, we call this kind of nodes as

MV node.

• Edges

E of the reduced network graph are used to

model the topology reconﬁguration. The series of

two switches, installed between two consecutive

MV substations, are mapped into a single edge of

the reduced graph

G (virtual breaker). Each edge

is associated with a label representing its state i.e.

close or open.

Figure 1 shows an example of the representation of

the network through the reduced graph

Ei.

Using the above notation we can introduce the fol-

lowing deﬁnitions:

Def. 1 (Radial Topology Constraint). A network

topology satisﬁes the Radial Topology Constraint iff

each MV substation is fed by only one HV substation

via only one path.

Def. 2 (Admissible Conﬁguration). A reduced

graph

Ei satisfying the radial topology con-

straint is said to be an admissible conﬁguration of the

network.

The graph representation

Ei is used to per-

form an algorithm that executes an exhaustive search

of all the admissible conﬁgurations of the network.

The details of the automatic procedure are described

in (Storti et al., 2014). The output of such procedure

is a list of binary strings (admissible conﬁgurations)

having length equals to the number of edges

E of

the reduced network graph. Each bit represents the

state of the corresponding edge (breaker). The net-

work topology is speciﬁed by an integer index, named

conf

, spanning the rows of the list of admissible con-

ﬁgurations ordered according to the automatic proce-

dure. During the optimization procedure, N

conf

con-

stitutes a nominal parameter to be optimized, so the

objective function can change abruptly moving from

a given conﬁguration to the previous or the next one,

making very challenging this optimization due to high

discontinuities in the objective function. For this rea-

son, in the following section, we present an heuris-

tic method to compare the graphs of two admissi-

ble topologies, in terms of active power loss values

through a purely topological analysis. This criterion

is used to deﬁne a suited ordering of the list of admis-

sible conﬁgurations, aiming to improve the continuity

of the objective function to the variation of the N

conf

parameter.

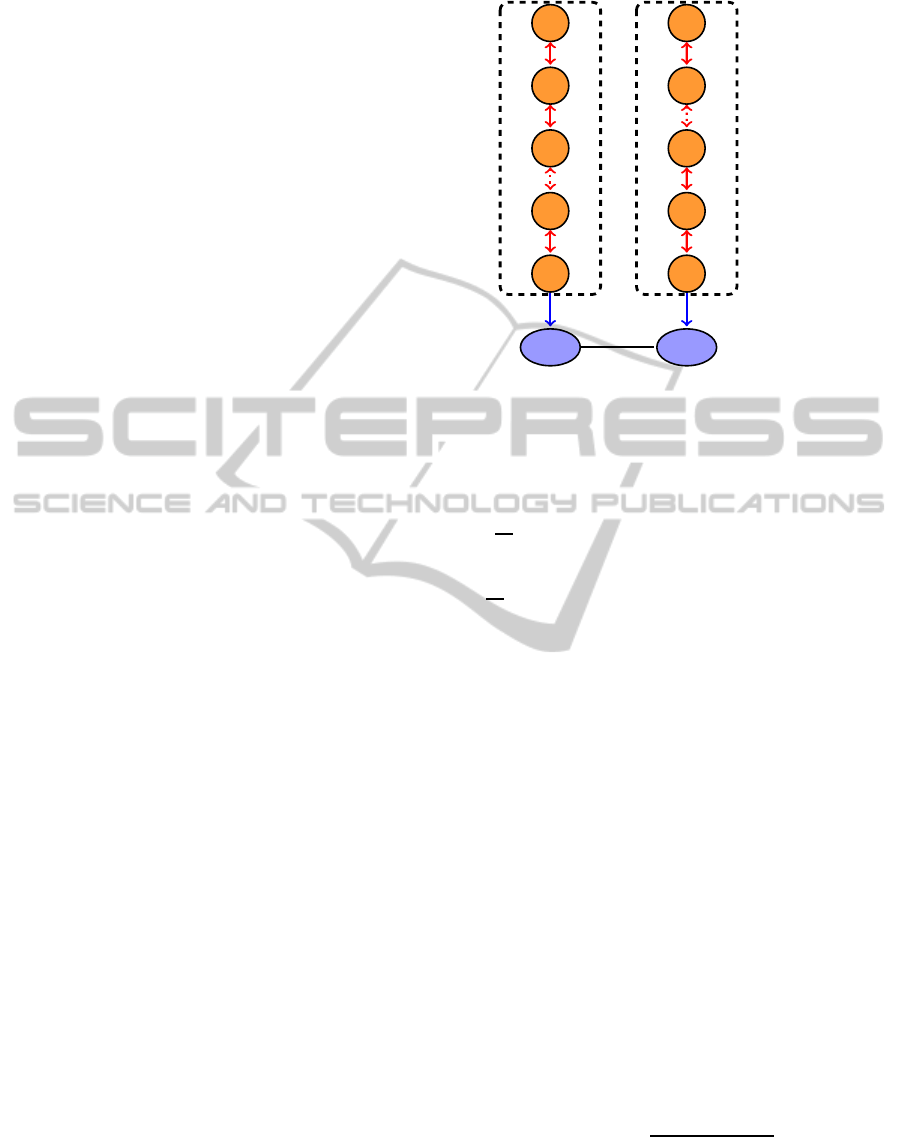
Figure 1: Example of the graph

Ei of the simpliﬁed

network. Orange circlesindicate MV nodes, gray rectangles

are HV nodes, dashed arrows represent open status edges.

The dashed box highlights a portion of the network.

4 ORDERING HEURISTIC

In order to make effective any algorithm for solv-

ing the optimization problem described in section 3.1,

we need an ordering heuristic of the admissible con-

ﬁgurations to improve the ’regularity’ of the objec-

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

276

tive function. In such a derivative free mixed inte-

ger context, it means reducing the variations of the

objective function evaluated at an admissible conﬁg-

uration i from the objective values at i − 1 and i + 1,

for i = 2,3,... ,n − 1, where n indicates the number

of the admissible conﬁgurations found as described

in the previous section.

4.1 Graph Representation of

Admissible Network Conﬁgurations

Each admissible conﬁguration of the network is iden-

tiﬁed by a binary string of length equal to the num-

ber of virtual breakers of the reduced graph. Given

a pair of conﬁgurations hi, ji, we use the Hamming

distance between the respective bit strings, d

(i, j),

to quantify the dissimilarity between i and j. Let

D be a square matrix of order n containing all the

Hamming distances between admissible conﬁgura-

tions, i.e. d

= d

(i, j) for i, j = 1, ...,n. Of course D

is symmetric with zeros along the diagonal only. Let’s

deﬁne as G

the undirected graph of the admissible

conﬁgurations represented by D, where each element

of the matrix is the weight w

of the edge e

that

connects nodes i and j of G

. Let’s denote by N

and E

the sets of nodes and edges of G

, respec-

tively. Figure 2 shows an example of the building pro-

cess of G

. The portion of the reduced graph con-

sidered in the example is highlighted within a dashed

box in Figure 1. Opening the virtual breaker between

nodes

and

represented by edge

3,4

, we ob-

tain the conﬁguration [1 1 0 1], while disconnecting

nodes

and

and reconnecting nodes

and

by opening the virtual breaker

2,3

and closing

3,4

the resulting conﬁguration is [1 0 1 1]. The extracted

conﬁgurations are two nodes of the graph G

at dis-

tance d

= 2.

4.2 Heuristic method for ordering the

admissible conﬁgurations

In this subsection we present an heuristic method,

based on G

, used to order the admissible conﬁgu-

rations of the network to avoid strong discontinuities

between active power loss values of consecutive con-

ﬁgurations. Then, in section 5 we will show how this

method applied to a real electrical network actually

makes less difﬁcult to solve the optimization problem

presented in section 3.1.

Given a conﬁguration i, the objective function value

F(k) will depend on all the other parameters values

in k, i.e. on a set of virtually inﬁnite combinations.

However we need to associate with each conﬁgura-

tion a unique scoring function, as an average estimate

1,2

2,3

3,4

4,5

1,2

2,3

3,4

4,5

1101 1011

= 2

Figure 2: Building process of conﬁgurations graph G

a portion of two instances of the reduced network graph

Ei.

of F(k). To this aim, the following reference values of

the real parameters are chosen for all conﬁgurations:

(

) = (k

j,min

+ k

j,max

)/2, j = 1,.. ., n (8)

and for the integer parameters:

(

) = [(k

h,min

+ k

h,max

)/2], h = 1,.. .,m (9)

in which the operator [·] indicates the round opera-

tion. For simplicity we will refer to f(i) to indicate

F(k)|

conf

and to

f(i) to represent the ﬁtness f(i)

computed in the reference values of the parameters

expressed in (8) and (9).

Let W be the list of all possible values for the weights

of the edges of graph G

, ordered in ascending man-

ner:

W = [w

,. .., w

]

Fixed a node i of G

and a weight w

∈ W, we de-

ﬁne (N

)

as the set of all nodes connected with i

by edges with weight w

. An estimate of the differ-

ence between

f(i) at i-th node and the objective val-

ues associated with the nodes belonging to (N

)

is given by the mean distance (∆F

)

between

f(i)

and the ﬁtness

f(k), ∀k ∈ (N

)

. Indicating as

(∆

i,k

)



f(i)−

f(k)



f(i) the relative distance be-

tween the ﬁtness

f(i) and the ﬁtness

f(k), the mean

distance can be mathematically expressed as:

(∆F

)

∑

)

k=1

(∆

i,k

)

(10)

where (l

)

is the cardinality of (N

)

. If each

node i of G

satisﬁes the following property:

(∆F

)

≤ (∆F

)

, j = 2,.. .,m (11)

AnOrderingProcedureforAdmissibleNetworkConfigurationstoRegularizeDFROptimizationProblemsinSmartGrids

277

we can deduce that, in mean, the active power loss

of the network varies less between similar conﬁgura-

tions than between dissimilar ones. Remember that

with ’similar’ we indicate similarity in terms of Ham-

ming distance. We can extract the subgraph G

i, whose set of edges E

is deﬁned as fol-

lows:

= {e

∈ E

s.t. w

= w

, (12)

∀i, j = 1, 2,...,n}

The existence of an edge between a pair of nodes i

and j of the graph G

should indicate that the con-

ﬁgurations i and j have close active power losses. In

the following section we will proof such property for

the network under analysis.

To order the admissible conﬁgurations of the network

we use the depth ﬁrst traversal algorithm on G

. The

order in which the nodes are visited will be the new

sequence of the indexes of the admissible conﬁgura-

tions.

5 TESTS AND RESULTS

In this section we ﬁrst empirically prove the property

expressed in (11) for the network under consideration,

then we compare the performances of GA when it

is used to solve the optimization problem presented

in section 3.1 for the considered electrical network,

whether the conﬁgurations are ordered or unordered.

Following the notation introduced in section 3.1

and network speciﬁcations described in section 2, we

can control the reactive power of the 5 generator sets

through the phase parameters φ. Instead it is not pos-

sible to control the reactive power of the photovoltaic

generator. Moreover it is possible to chose the N

tap

value of the TVR and the conﬁguration of the net-

work selecting it from the set of admissible ones pre-

viously determined. The phases of the 5 generator

sets φ

,φ

will be spanned in a real given

range speciﬁed by the capability functions of the cor-

responding generator sets. The tap N

tap

of the TVR

will be spanned in the discrete (normed) range de-

ﬁned in (1). Finally,according to the list of admissible

conﬁgurations introduced in section 3.2, the network

topology is speciﬁed by an index, N

conf

, spanning the

rows of such list. In particular, in the smart grid un-

der consideration, the number of admissible conﬁgu-

rations is 390. Summarizing, the candidate solution

vector k = [φ

,φ

tap

conf

] will span the

set deﬁned below:

A = { k ⊂ R

× Z × X : −0.2 ≤ φ

,φ

≤ 0.45

−0.2 ≤ φ

≤ 0.55

0.0 ≤ φ

≤ 0.64

−0.32 ≤ φ

≤ 0.45

−3 ≤ N

tap

≤ 3

conf

∈ X }

in which X = {conf

,..., conf

390

} is the set of indexes

of all conﬁgurations. Moreover, in order to be valid,

a solution k must satisfy the constraints on voltages

and currents deﬁned below:

B =



k ⊂ R

× Z × X : 0.9V

nom

≤ V

(k) ≤ 1.1V

nom

, j = 1, ..,M



C =



k ⊂ R

× Z × X : |I

(k)| ≤ I

max

, j = 1,..,R



in which M and R represent the total number of

nodes and branches of the real network, respectively,

whereas V

nom

and I

max

are the nominal value of the

voltage of the j-th node and the maximum current al-

lowed in the j-th wire, respectively.

Performing the analysis described in the previous

section, we found that in the network under consid-

eration there are only three different possible weights

(i.e. Hamming distance values) associated with the

edges of the graph of the admissible conﬁgurations

. In particular:

W = [2,4,6]

whereby we have to compute (∆F

)

, (∆F

)

, (∆F

)

for i = 1,2,. .. ,390. The minimum weight belong-

ing to W is w

min

= 2, as we could expect, since in

a real electrical network, a topology change implies,

at least, closing a given breaker and opening another

one. Thus, we have to check if the following two con-

ditions are satisﬁed:

(∆F

)

≤ (∆F

)

i = 1,...,390 (13)

(∆F

)

≤ (∆F

)

i = 1,...,390 (14)

To compute the ﬁtness value associated with each

node of G

, we have considered as input of the

network model the power proﬁle associated with the

1:00PM (one hour) of the 1-st of January.

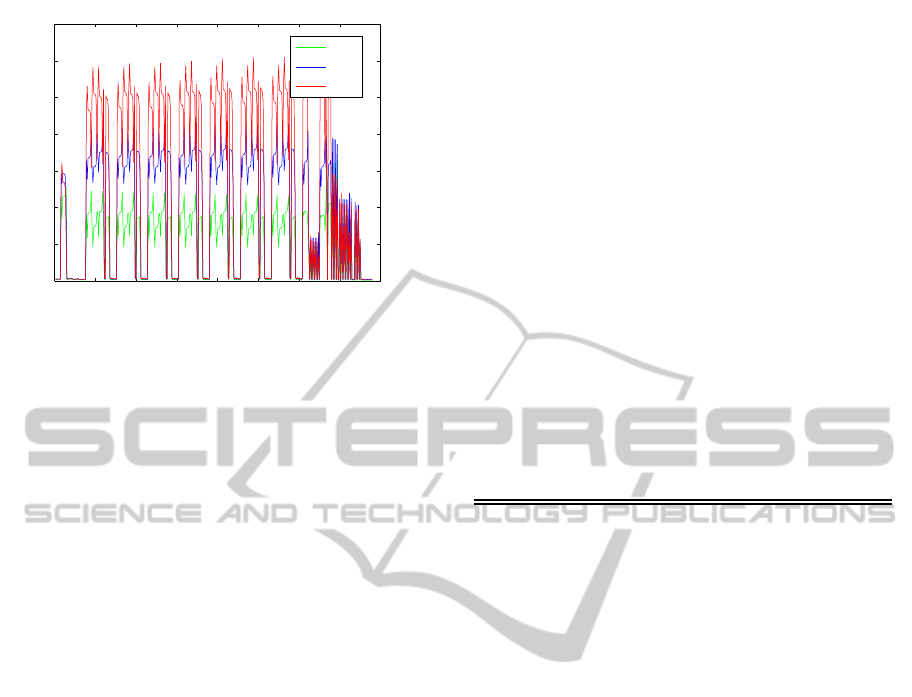
Figure 3 shows the values of (∆F

)

, (∆F

)

, (∆F

)

calculated for all nodes of G

. It is possible to ob-

serve that, for most of nodes, relations (13) and (14)

are satisﬁed. An accurate data analysis returns that

over 97% of nodes (network conﬁgurations) satisfy

these two relations.

It’s important to point out that this result doesn’t de-

pend on the values initially assigned to ﬁtness param-

eters

for j = 1,.. .,5 and N

tap

. In fact, the set of

nodes satisfying relations (13) and (14) is the same for

any set of admissible values initially assigned to these

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

278

0 50 100 150 200 250 300 350 400

100

120

140

nodes i=1,2,...,390

(∆F

)

(∆F

)

(∆F

)

Figure 3: Mean distance between the ﬁtness value associ-

ated with node i,

f(i), and ﬁtness values associated with

all the adjacent nodes of the i-th node belonging to (N

)

, (N

)

respectively, for i = 1,2, ... ,390. The scale

factor is equal to

f(i).

parameters. Thus, we have empirically proven Equa-

tion (11), speciﬁcally that similar network conﬁgura-

tions (i.e. nodes of graph G

connected by edges

with small weights) correspond to close active power

loss values. Note that we have veriﬁed this property

only for the network under analysis.

At this point, as described in section 4.2, we

can choose a depth ﬁrst traversal of the sub graph

i to order the admissible conﬁgura-

tions. It was veriﬁed that G

is a connected graph,

with size, i.e. the number of its edges, equal to 4743.

In particular, the minimum degree of G

, i.e. the

minimum number of edges incident to its nodes, is

equal to 21. There are 90 nodes having this num-

ber of edges incident to them. The maximum degree

of G

is 37 and only 20 nodes have this number of

edges incident to them. In order to compare the effec-

tiveness of this ordering heuristic technique in solving

the proposed optimization problem, the execution of

GA is repeated 6 times, whether the conﬁgurations

are ordered or unordered. Different executions con-

sider different sequences of indexes obtained through

depth ﬁrst traversal of G

, starting from different

root nodes.

To compare performances of GA, the algorithm

parameter setting is chosen identical whether the con-

ﬁgurations are ordered or unoredered (in the second

case, we consider the initial ordering of the admis-

sible conﬁgurations returned by the automatic proce-

dure described in (Storti et al., 2014)). In particular,

the number of individuals of a population is set to 20.

The elite individuals are 2, i.e. only 2 individuals in

the current generation are guaranteed to survive to the

next generation. The crossover fraction parameter is

0.8. The mutation operator is applied to the remain-

ing individuals. Furthermore, the α and β coefﬁcients

used in expressions (6) and (7) are set to 0.9 and 0.2,

respectively.

The maximum number of iterations before the algo-

rithm halts is 100, but GA can stop if the weighted

average relative change in the ﬁtness value over 50 it-

erations is less than or equal to 10

−9

All performed tests consider the same states of the

network to seed GA. More precisely, a ﬁxed initial

population is considered for all of the executions of

the GA when the admissible conﬁgurations are or-

dered and unordered. It should be noted that the ran-

dom initialization does not necessarily ensure the sat-

isfaction of the constraints consideredin the deﬁnition

of the chosen ﬁtness function. Results of the simu-

Table 1: Mean number of generations (# gen) produced by

GA to return the optimal solution, mean percentage reduc-

tion of the ﬁtness value (%F reduct.), mean reduction of the

active power loss (P

loss

) whether the admissible conﬁgura-

tions are ordered or unordered.

ordered conf. unordered conf.

# gen 73 67

%F reduct. 0.023 0.022

loss

reduct. [W] 1096.97 1088.34

lations are shown in Table 1. It compares the mean

value of the number of generations created (#gen),

the ﬁtness percentage reduction (%F reduct.) and the

reduction of active power loss of the network (Ploss

reduct.), whether the conﬁgurations are ordered or un-

ordered (Storti et al., 2014). More precisely, last two

indicators consider the reduction of the ﬁtness value

and actual active power loss between the optimal so-

lution and the best individual of the initial population.

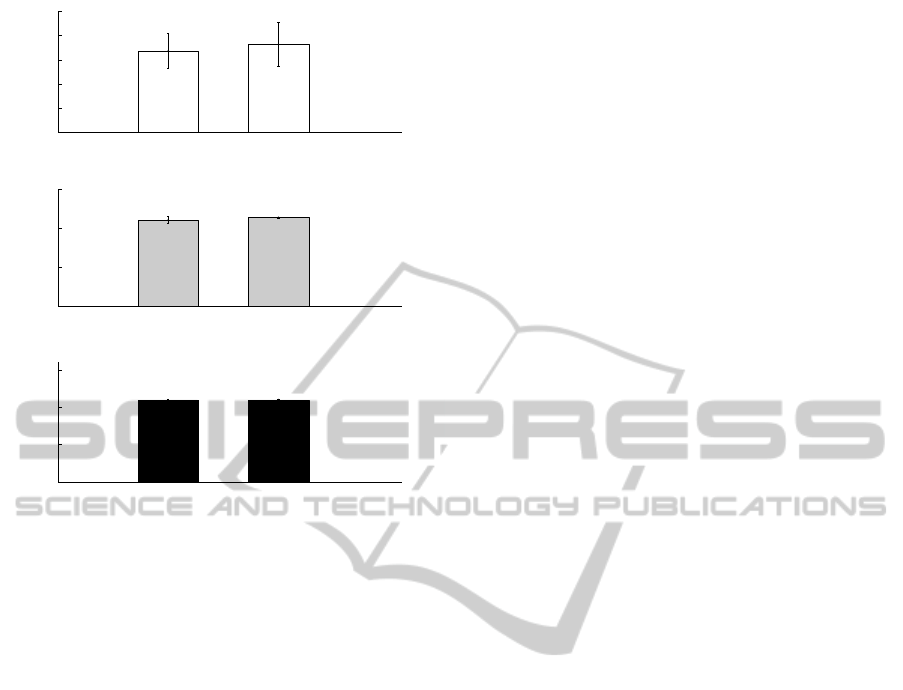
Moreover, Figures 4 (a)-(b)-(c) show the mean value

of the number of generations, the mean percentage

reduction of ﬁtness value and the mean reduction of

power loss and the respective standard deviation in

both cases of ordered and unordered list of conﬁgura-

tions.

We can note that the mean number of generations

of GA when the conﬁgurations are ordered is larger

than in the unordered case. This is due to greater

headway made by GA during the search process of

the optimal solution, in the ﬁrst case. This allows to

have, on average, an higher reduction of the ﬁtness

value, as well as of the total active power loss, from

the initial state of the considered network. As we ex-

pected, the power loss reduction is not very high, but

considering that all the tests simulate only one hour

of one day and projecting this power loss reduction

to the whole network over time, the savings could be-

come interesting in the regular operating condition of

the real network in which the value of the power loss

AnOrderingProcedureforAdmissibleNetworkConfigurationstoRegularizeDFROptimizationProblemsinSmartGrids

279

Not Ord. Config. Ord. Config.

100

Generation

(a)

Not Ord. Config. Ord. Config.

0.01

0.02

0.03

Fitness reduction (%)

(b)

Not Ord. Config. Ord. Config.

500

1000

1500

AP Loss Reduction [W]

(c)

Figure 4: Mean value of the number of generations (a), the

mean percentage reduction ﬁtness value (b) and the mean

reduction of active power loss (c) with the respective stan-

dard deviation for ordered and unordered list of conﬁgura-

tions.

becomes considerable.

6 CONCLUSIONS

In this paper an improvement of the control system

described in (Storti et al., 2013a), (Possemato et al.,

2013), (Storti et al., 2013b) and (Storti et al., 2014) is

presented. We propose an heuristic method to com-

pare admissible network topologies and a criteria to

order the list of such topologies aiming to improve the

continuity of the objective function to the variation of

the conﬁguration parameter. We execute some tests

on the SG sited in the west area of Rome realized by

ACEA Distribuzione S.p.A.. Results show that, for the

network under analysis, the proposed ordering pro-

cedure makes the joint PFC and DFR optimization

problem simpler to cope with a plain genetic algo-

rithm. In future works we intend to verify the criteria

in a more complex network and at different time inter-

vals. Moreover, by exploiting the property described

by Equations 13 and 14, it is possible to redeﬁne more

suitable mutation and crossover operators to furtherly

improve the convergence of the GA during the evolu-

tionary process.

REFERENCES

Carreno, E., Romero, R., and Padilha-Feltrin, A. (2008). An

efﬁcient codiﬁcation to solve distribution network re-

conﬁguration for loss reduction problem. IEEE Trans-

action on Power Systems, 23(4):15421551.

Chandramohan, S., Atturulu, N., Kumudini, R., and Ven-

takesh, B. (2010). Operating cost minimization of

a radial distribution system in a deregulated electric-

ity market through reconﬁguration using nsga method.

International Journal of Electric Power Energy Sys-

tems, 32(2):126132.

Civanlar, S., Grainger, J., Yin, H., and Lee, S. (1988).

Distribution feeder reconﬁguration for loss reduc-

tion. IEEE Transactions on Power Delivery,

3(3):12171223.

Dahu, L. (2011). Electric power communication system of

the future smart grid. Telecommunication for Electric

Power System, 32(222).

Merlin, A. and Back, H. (1975). Search for minimum-

loss operational spanning tree conﬁguration for urban

power distribution systems. In Proceeding of Fifth

power system conference (PSCC), page 118.

Nara, K., Shiose, A., Kitagawa, M., and Ishibara, T. (1992).

Implementation of genetic algorithm for distribution

systems loss minimum reconﬁguration. IEEE Trans-

action on Power Systems, 7(3):10441051.

Possemato, F., Storti, G., Paschero, M., Rizzi, A., and Frat-

tale Mascioli, F. (2013). Two evolutionary computa-

tion approaches for active power losses minimization

in smart grids. In Proceedings of North America Fuzzy

Information Processing Society.

Singh, M., Khadkikar, V., Chandra, A., and Varma, R.

(2011). Grid interconnection of renewable energy

sources at the distribution level with power-quality

improvement features. IEEE Transactions on Power

Delivery, 26(1):307–315.

Storti, G., Possemato, F., Paschero, M., Alessandroni, S.,

Rizzi, A., and Mascioli, F. F. (2013a). Neural Nets

and Surroundings 22nd Italian Workshop on Neu-

ral Nets, WIRN 2012, May 17-19, Vietri sul Mare,

Salerno, Italy, volume 19 of Smart Innovation, Sys-

tems and Technologies, chapter Active power losses

constrained optimization in Smart Grids by gentic al-

gorithms, pages 279–288. Springer Berlin Heidelberg.

Storti, G., Possemato, F., Paschero, M., and nad F.M. Frat-

tale Mascioli, A. R. (2014). A radial conﬁgurations

search algorithm for joint pfc and dfr optimization in

smart grids. In Proceeding of 23th international con-

ference on industrial electrincs (ISIE).

Storti, G., Possemato, F., Paschero, M., Rizzi, A., and Frat-

tale Mascioli, F. M. (2013b). Optimal distribution

feeders conﬁguration for active power losses mini-

mization by genetic algorithms. In Proceedings of

North America Fuzzy Information Processing Society.

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

280