
Combining Piecewise Linear Regression and a Granular Computing
Framework for Financial Time Series Classification
Valerio Modugno
1
, Francesca Possemato
2
and Antonello Rizzi
2
1
Dipartimento di Ingegneria Informatica, Automatica e Gestionale (DIAG)
SAPIENZA University of Rome, Via Ariosto 25, 00185, Rome, Italy
2
Dipartimento di Ingegneria dell’Informazione, Elettronica e Telecomunicazioni (DIET)
SAPIENZA University of Rome, Via Eudossiana 18, 00184, Rome, Italy
Keywords:
Time Series Classification, Evolutionary Optimization, Granular Computing, Linear Piecewise Regression,
Sequential Pattern Mining, Algorithmic Trading.
Abstract:
Finance is a very broad field where the uncertainty plays a central role and every financial operator have to
deal with it. In this paper we propose a new method for a trend prediction on financial time series combining a
Linear Piecewise Regression with a granular computing framework. A set of parameters control the behavior
of the whole system, thus making their fine tuning a critical optimization task. To this aim in this paper we
employ an evolutionary optimization algorithm to tackle this crucial phase. We tested our system on both
synthetic benchmarking data and on real financial time series. Our tests show very good classification results
on benchmarking data. Results on real data, although not completely satisfactory, are encouraging, suggesting
further developments.
1 INTRODUCTION
Prediction of price movements of a security is a very
hard task. A well known economic theory, the Effi-
cient Market Hypothesis (EMH) (Malkiel and Fama,
1970) states that, in an informationally efficient mar-
ket, price changes are unforeseeable if they fully in-
corporate the information and expectations of all mar-
ket participants. The more efficient is a market, the
more random is the sequence of price changes gener-
ated by such a market. So, in principle, the EMH does
not allow to make predictions about future behaviors
of a financial time series and the evolution of a stock
or a bond are modeled as a random walk.
Over the years this hypothesis gaverise to a strong
debate about its credibility and a lot of researchers
have disputed the efficient market hypothesis both
empirically and theoretically. Among the EMH skep-
tics it is possible to cite two works (Haugen, 1999),
(Los, 2000) in which the authors show the deficiency
of the theory by analysing the behaviour of six Asian
markets. In their work the authors do not find any
empirical confirmations of EMH. These results give
a chance to some market operators to realize a gain
exploiting information on past behavior. One of the
most common approaches used by brokers is called
Technical Analysis (TA). TA consists in a large tool
set that is used to predict market movements. One
of the most common tools of TA is the Chart Pattern
Analysis: technicians try to discover patterns from the
market price graph and use this information to buy or
sell assets. This approach appears to be very ineffi-
cient because of the subjectivity that guides the se-
lection of patterns inside data. Today the mainstream
research on the financial field employs a lot of soft
computing techniques to face the challenging prob-
lem of market behaviour prediction. Considering the
classification proposed in (Vanstone and Tan, 2003) it
is possible to gather each method in one of the subse-
quent categories:
• Time Series Prediction: forecasting time series
points using historical data. Research in this area
generally attempts to predict the future values of
time series. Possible approaches comprise raw
time series data, such as Close Prices, or time
series extracted from base data, like the indica-
tors employed in TA. Some examples are: (Chang
et al., 2009), (Radeerom et al., 2012).
• Pattern Recognition and Classification: extraction
of significant known patterns inside data and us-
age of such patterns to attempt a classification
problem. Some examples are: (Nanni, 2006), (Sai
281
Modugno V., Possemato F. and Rizzi A..
Combining Piecewise Linear Regression and a Granular Computing Framework for Financial Time Series Classification.
DOI: 10.5220/0005127402810288
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 281-288
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

et al., 2007), (Cheng et al., 2010).
• Optimization: solving problems where patterns in
the data are not known a priori. Research in this
area goes from the optimal selection of the param-
eters of soft computing systems, to the extraction
of the optimal point at which to enter transactions.
One example is (Kendall and Su, 2005).
• Hybrid: this category is used to identify research
which attempts to combine more than one of the
previous categories. One example is (Bagheri
et al., 2014).
In this paper we introduce a newHybrid Classification
Algorithm based on a Piecewise Linear Regression
(PLR) preprocessing of raw data within a Granular
Computing (GrC) framework (Bargiela and Pedrycz,
2003). From a structural point of view our work has
something in commonwith (Sai et al., 2007), in which
the authors apply a feature selection on several TA in-
dicators and use the extracted features subset to train
a Support Vector Machine for classification purposes.
However, in this paper we do not use any technical in-
dicator as input,trying to identify some recurrent pat-
terns in the raw data prices sequence through PLR and
a GrC algorithm. This approach shares some features
with (Chang et al., 2009). In particular the main fea-
tures of the proposed work are:
1. our approach analyses the financial data at differ-
ent time scales since we can control the granular-
ity of the PLR preprocessing stage;
2. we employ a Dynamic Time Warping dissimilar-
ity measure that manages very well the presence
of noise in data set;
3. our method handles the phenomenon of errors in
the labeling procedure, which is very common in
a financial application, due to the fact that certain
types of heuristics are generally used to describe
a financial time series;
4. our approach is conservative in the sense that it re-
duces the risk of economic loss by rejecting, dur-
ing the pattern discovery phase, all the sequences
that do not have informative contents.
The rest of the article consists of four parts. In the
first part we provide a description of the problem def-
inition, as well as, the hypothesis settings; in the sec-
ond part we present the system GRASC-F (GRanular
computing Approach for Sequences Classification-
Financial application), focusing on the preprocessing
stage and the rejection policy in the embedding pro-
cedure; in the third part we show the results obtained
by applying the algorithm to synthetic data with dif-
ferent kinds of noise and show some test results on
real stocks. Finally some comments are reported in
the conclusion section.
2 PROBLEM DEFINITION
In this paper we propose a method that is conceived to
bring a reliable approach to market trend predictions
in financial time series. We refer to market trends
as tendencies of a market to move in a particular di-
rection. So through our method we want to identify
ordered behaviors of the market that technicians in-
dicate with the terms bull market, when they speak
about an upward trend, and bear market, when they
refer to a downward trend. This algorithm can work
alone or as a trading assistant to support the buy and
sell asset operations of a financial operator. Due to
the overall complexity that arises when we face this
kind of problems, it is necessary to make some sim-
plifying assumptions. First of all we deny the EMH
that refuses the existence of solid trends inside finan-
cial markets considering them only as random fluctu-
ations. Instead, we take on two simple principles that
are the bases of all the TA:
• prices move in trends up and down;
• history tends to repeat itself, and the collective
mood of the investor works always in the same
manner, impressing specific patterns on price
graphs that act as fingerprints. We can use this
information to make trend prediction.
In this work we represent a financial time series as
a sequence of trends: raw financial data are prepro-
cessed to extract trend objects that become the ba-
sic information units for the GrC-based data mining
procedure. Therefore, the preprocessing stage plays
a central role and is significant for the overall per-
formance of the classification system. After the pre-
processing phase we have to deal with a sequence of
structured objects and two different kinds of problems
arise:
• the selection of significant patterns inside the se-
quence of structured data;
• the labeling of unlabeled sequences of trends.
For the first problem we use a featureless GrC frame-
work to describe structured data: dissimilarities be-
tween subsequences of variable lengths and a cluster-
ing procedure are used to select the best representa-
tives for all the sequences according to some given
criteria. Therefore, chosen the correct dissimilarity
measure, we can identify a set of prototypes (called
”Alphabet”) and project all the sequences data in this
prototypes space, where it is easier to accomplish a
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
282

classification task. The labeling problem is faced con-
sidering the overall trend of a fixed time window of
the raw data. In this paper we will not take care about
the cost of transaction, taxes and other losses which
take place during the common market operations, be-
cause we only want to prove the reliability of the clas-
sification algorithms and taking into consideration all
the economic aspects in future works.
3 THE GRASC-F SYSTEM
In this Section we describe in detail the structure of
the whole classification system GRASC-F, focusing
our attention on all the aspects that concern the fi-
nancial prediction task. The system GRASC-F is
an evolution of GRAPSEC (Rizzi et al., 2013), a
sequences classification system based on GrC algo-
rithms GRADIS (Livi et al., 2012) and RL-GRADIS
(Rizzi et al., 2012). These are data mining procedures
able to discover consistent patterns of variable-length
that occur frequently in a data set. The computation of
the prototypes through a clustering technique is cen-
tral in GRASC-F system: a further refining stage is
performed in order to remove prototypes with low re-
currence; all the prototypes that are retained become
part of the so-called symbols alphabet A. We base
the new representation of the input data on the alpha-
bet A. The alphabet is extracted with an unsupervised
technique.
Since the alphabet building phase depends on the
choice of a dissimilarity measure, in this paper we de-
cide to use the DTW (Berndt and Clifford, 1994) dis-
tance, because the preprocessed sequences data are
made by complex objects belonging to R
n
. More-
over, DTW similarity measure is resilient to noise.
GRASC-F depends upon a lot of different parame-
ters and in order to obtain a good performance of the
whole classification process, a fine tuning of them be-
comes a critical task. We get rid of this problem in-
cluding an optimization phase inside the classification
system, which aims to automatize the setting of the
(relevant) parameters.
From a general point of view, the GRASC-F sys-
tem can be described as a pipeline of four main
blocks: financial time series pre-processing, alphabet
building, sequence data projection, and classification.
During the preprocessing stage the input row data is
transformed into sequences of trends. Then we la-
bel every sequence by means of an empirical heuris-
tic. The alphabet building step is performed through
RL-GRADIS algorithm. The developed alphabet A
is successively used to represent the input sequences,
building the so-called symbolic histograms represen-
tation. Finally, a suited feature-based classifier, in our
case a simple K-NN , is adopted to work directly on
this new representation. All these steps are repeated
inside an optimization cycle until the process hits one
of the stop conditions. In this paper we use a genetic
algorithm as optimization procedure. Figure 1 shows
the overall structure of the GRASC-F classification
system.
Figure 1: GRASC-F Classification System.
3.1 Preprocessor
Data preprocessing occupies the first step of the
whole classification system. This phase aims to rep-
resent raw data about the prices of a stock as a labeled
sequences database of trends. The main preprocess-
ing steps are:
• Linear Piecewise Regression
• Labeling of sequences
In the following Sections we will describe briefly the
preprocessing phases.
3.1.1 Linear Piecewise Regression
First we collect raw data about the prices of a stock,
in a fixed time interval, from a specific data file. Dur-
ing the acquisition of the data, we consider a con-
stant sampling rate and for each sample we choose the
close price. Then, the obtained time series is normal-
ized between zero and a fixed maximum value. At this
point we perform a trend extraction on the time series,
using the technique described in (Muggeo, 2003).
This method, that is freely available as an R package,
takes as input a time series and returns a sequence of
trends using a procedure of breakpoints detection. A
breakpoint describes a sample time at which a trend
stops and a new one starts. Since in our application
we do not know a priori the number of breakpoints on
the input time series, we decided to use the algorithm
described in (Muggeo, 2003) because it performs well
in this kind of situations. Practically, we set an ini-
tial number of breakpoints candidates that we call bp
on the stock price function, then, after some itera-
tions of the algorithm, we obtain a segmented linear
regression with the most reliable breakpoints, while
the other are dropped off. The number of breakpoints
CombiningPiecewiseLinearRegressionandaGranularComputingFrameworkforFinancialTimeSeriesClassification
283
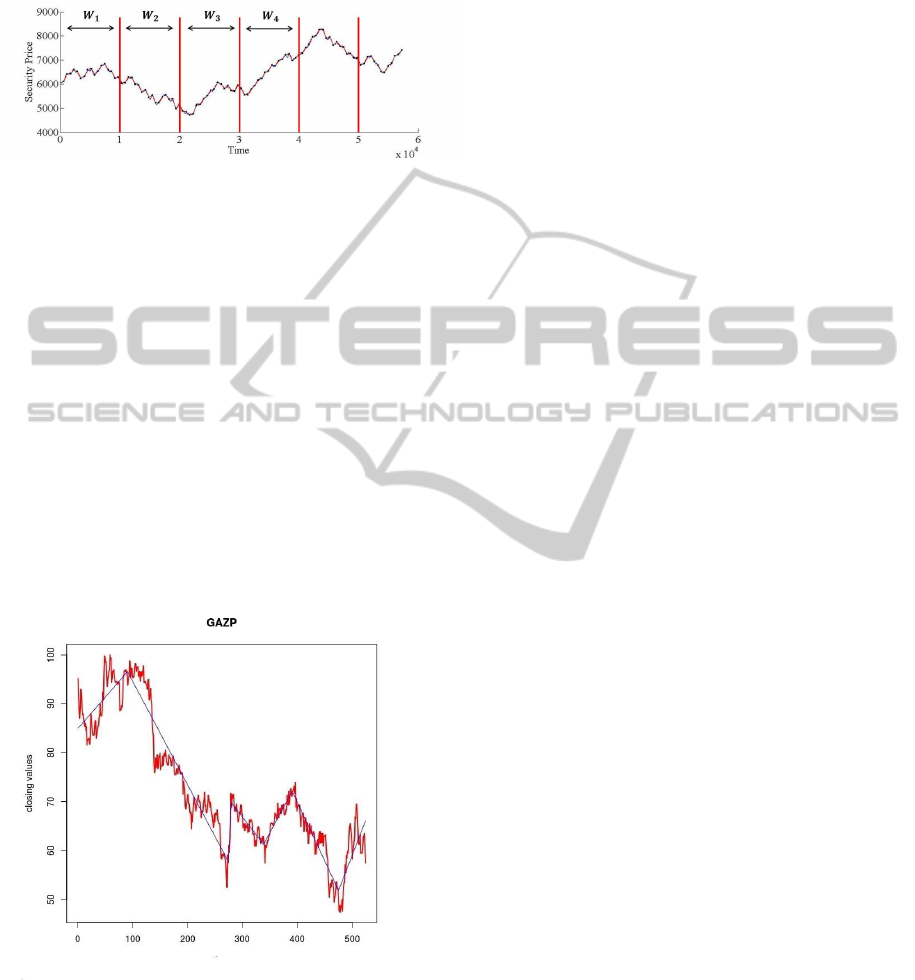
candidates determines the scale of the linear segmen-
tation. The more are the points, the more accurate is
the segmentation of the time series. The output of the
Figure 2: Sequences extraction from preprocessed time se-
ries using a fixed time window W.
LPR is a sequence of trends. Each trend is described
by two real values: the slope of the current trend and
its duration expressed in number of ticks. Therefore
the sequence is constituted by objects that belongs to
the R
2
space. Before the learning phase, we normal-
ize each element of the sequence in the [0, 1] range.
Then, the entire preprocessed data set is divided into
different sequences of R
2
objects, considering a non
overlapping time window W
i
made by a fixed number
of time samples on the input time series. For exam-
ple if we take a window of 1000 ticks (see Figure 2),
then all the trends that are extracted from that win-
dow become a sequence. Therefore, the preprocessed
data set is made by sequences of different number of
objects, depending on how many trends are detected
by the preprocessor in that window. In Figure 3 it is
Figure 3: Example of the LPR applied to a real raw data of
closing prices of a stock.
possible to observe an example of the LPR applied to
a single window of a real raw data.
3.1.2 Labeling of Sequences
In the second step of the preprocessing, we label the
sequences previously extracted. Consider a sequence
s
i
computed from the time window W
i
of n
t
ticks and
a time window W
i+1
that follows W
i
with the same
number of ticks. In order to establish the label of s
i
,
we read the open value p
w
i+1
1
and the close value p
w
i+1
n
t
of the original time series that belongs to W
i+1
. Then
the label l
i
of s
i
is computed as:
l
i
=
0 if p
w
i+1
n
t
− p
w
i+1
1
≤ 0 (1)
1 otherwise
Thus if the label l
i
is equal to 0 it means that
the sequence s
i
anticipates a downward trend in the
next time window, otherwise it anticipates an upward
trend. From the practical trading point of view, a clas-
sification model able to predict such labels with a suf-
ficient accuracy could be used to raise sell and buy
signals. We repeat this procedure for each sequence
of the database extracted in the previous phase except
for the last one because we cannot label it. Finally,
we divide the sequences database into three sets: the
training set S
tr
, the validation set S
vs
and the test set
S
ts
.
3.2 Symbols Alphabet
We define our training set S
tr
= {s
1
, s
2
, ..., s
n
} as a
list of sequences, choosing the DTW distance as the
dissimilarity measure d : S × S → [0, 1] for the GrC-
based features mining procedure. Through a cluster-
ing algorithm and using d(·, ·) we identify a finite set
of symbols A = {a
1
, a
2
, ..., a
n
}; the clustering proce-
dure that we employ, is the well-known Basic Sequen-
tial Algorithmic Scheme (BSAS) algorithm. From
each sequence we build a set of variable-length subse-
quences that is obtained by slicing the sequence con-
sidering its contiguous elements only. We repeat the
slicing operation, extracting all the subsequences with
a length value between two user defined parameter
namely l and L, which define respectively the min-
imum and the maximum number of contiguous el-
ements that compose each subsequence. After the
expansion phase, in which we generate all the sub-
sequences (from now on we refer to this new set as
N ), a clustering procedure is executed on N multi-
ple times. In BSAS we have to set a scale param-
eter θ, taking values in the [0, 1] interval and con-
trolling the maximum radius allowed for all the clus-
ters in the final partition. For information compres-
sion purpose we decide to use the Minimum Sum
of Distances (MinSOD) technique to represent com-
pactly every cluster C
j
with only one element η
j
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
284

selected in the cluster. In GRASC-F we decide to
use RL-GRADIS as mining algorithm because it im-
proves the overall computational performance dur-
ing the clustering-based symbols alphabet extraction
phase. The main idea is to track the evolution of
the cluster construction when the input stream N is
analyzed. RL-GRADIS maintains a dynamic list of
receptors, constituted by the MinSOD cluster repre-
sentatives and characterized by an additional parame-
ter called firing strength denoted as f ∈ [0, 1], which
is dynamically updated by means of two additional
parameters: α, β ∈ [0, 1]. The α parameter is used
as a reinforcement weight factor each time a recep-
tor/cluster ¯r is updated, i.e., each time a new input
subsequence is added to the receptor/cluster. The β
parameter, instead, is used to model the speed of for-
getfulness of receptors. In this way, the clusters that
are not frequently updated during the alphabet con-
struction phase are discarded and we only retain the
clusters that show a good firing strength.
3.3 Embedding Procedure
After the computation of the symbols alphabet A we
proceed with the embedding phase that consists to
map the input sequences in S to a new R
d
space,
where d is the number of symbols that belongs to A
and we refer to it as feature space. In this new space
each input sequence s
i
is represented as a real-valued
vector called symbolic histogram h
(i)
∈ R
d
. The j-
th component of h
(i)
represents the number of occur-
rences of the symbol a
j
∈ A into s
i
. To recognize
if an instance of a symbol a
j
appears within an in-
put sequence s
i
we use an inexact matching proce-
dure based on d(·, ·). For more information about the
matching procedure we suggest to read (Rizzi et al.,
2013). Specifically, in GRASC-F, after the embed-
ding procedure, a second analysis stage is performed
on the symbolic histograms, that we refer to as reduc-
tion phase. In this step, we search for all the subse-
quences s
i
which are mapped to symbolic histogram
with all zero entries. Every time we found such a se-
quence, we remove it from the data set only for the
current individual fitness evaluation. In fact, we made
the assumption that if there are no symbols in a se-
quence, it means that it is not significant and, from a
financial trading point of view, it corresponds to a sit-
uation where the price of a certain security stalls and
there are no emerging behaviors inside data that can
be useful for prediction purposes. So, to be conser-
vative, we prefer to clear off the data set from every
sequence that does not bring any predictive informa-
tion based on the current alphabet A.
3.4 Optimization
The GRASC-F classification system depends on some
parameters that control the behavior of the whole sys-
tem. In order to choose the best setting for these
parameters, we decide to introduce an optimization
step that maximizes the classification performance on
a validation set. These parameters affect the function-
ality of every single stage that composes the system.
In the following we list all the parameters to be tuned
in order to improve the final performance:
• bp: the number of presumed breakpoints that con-
trol the scale of granulation of LPR;
• Q: the maximum number of receptors;
• α: the reinforcement factor when the cluster is up-
dated;
• β: the speed of forgetfulness of receptors;
• ε: the threshold to remove not-frequently updated
receptors;
• θ: the threshold to decide whether a subsequence
is added to an existing receptor/cluster or to a new
one;
• σ: the default strength value for new receptors.
To this aim we introduce an automatic optimiza-
tion procedure using a suited genetic algorithm. We
use a cross-validation strategy to evaluate the fitness
function guiding the optimization, by computing the
recognition rate achieved on the validation set S
vs
. In
this paper, we incorporate the preprocessing stage in-
side the optimization routine to optimize also the pre-
processor parameter bp. We pay in terms of com-
putational effort, that impacts on the training time
but on the other hand we are able to find the opti-
mal time scale for sequences representation. In this
way, we obtain a sort of multi-resolution approach al-
lowing the automatic identification of the time scale
which minimizes the classification error on the S
vs
.
In other words we choose the observation scale cor-
responding to the best informative process represen-
tation. Then, after the preprocessing step, the initial
data set is split into a validation set S
vs
and a training
set S
tr
. At this point we extract a symbols alphabet A
l
from S
tr
. By using the computed A
l
, the input training
and validation sequences are embedded by means of
the symbolic histograms representation. During the
embedding phase we strip away all the sequences in-
side S
vs
and S
tr
that has all zeros inside the symbolic
histogram and, after that, we obtain a reduced embed-
ded training set and a reduced embedded validation
set. Finally, we compute the per-class recognition rate
CombiningPiecewiseLinearRegressionandaGranularComputingFrameworkforFinancialTimeSeriesClassification
285

using a K-NN classifier on the reduced embedded val-
idation set. The fitness value f is thus given by
f = 1−
1
n
n
∑
i=1
#err
i
#patt
i
, (2)
in which #err
i
is the number of misclassified patterns
of class i and #patt
i
is the total number of patterns of
class i, i = 1, ..., n. The optimization stage stops if
the fitness value reaches a predefined value or after a
maximum number of generations of the optimization
algorithm.
4 TESTS AND RESULTS
In this section we present some experiments that we
performedin order to test the behaviour of the classifi-
cation system in different operational situations. First
we analyse classification results using synthetic data
set, then we evaluate the performance of the system
using four real financial time series.
4.1 Synthetic Data Set Generation
The aim of this section is to test the effectiveness and
performance of the GRASC-F system in a synthetic
and controlled environment. In order to analyze the
behavior of the algorithm, we use a synthetic data
generator. The output of the generation process is a
time series over a predefined time interval, represent-
ing the prices valuesof a fictitious stock at a fixedtime
sampling. As described in Section 3.1.2, we consider
two possible classes for the sequences: upward and
downward trends. The domain D of the sequences is
defied as D =
[x, y]
T
∈ R
2
| − 60 ≤ x ≤ +60, 5 ≤
y ≤ 30
, where x models the slope and y the duration
of a trend.
The data are generated through three main steps per-
formed for each class:
• Frequent sequential pattern generation. For each
of the two possible classes, a set of n
pat
sequences
of objects in D (the symbols, i.e. frequent pat-
terns) are generated. The size of each pattern is
randomly determined using a normal distribution
with user defined mean l
pat
and standard deviation
σ
p
. These patterns should be considered as sell or
buy signals for the trading system.
• Sequential database generation. A database of
n
seq
sequences of trend and duration is built us-
ing the previously determined frequent patterns.
The size of each sequence size
seq
represents the
number of frequent patterns in each sequence.
• Labelling of sequences. A labelling sequence of
duration equal to size
seq
·t
pat
is generated for each
sequence in the database in order to assign a la-
bel to it. If the sequence represents a downward
trend, the domain D
down
of the corresponding la-
belling sequence is defined as D
down
=
[x, y]
T
∈
R
2
| −60 ≤ x ≤ +30, 5≤ y ≤ 30
; if the class of
the patterned sequence indicates an upward trend,
the domain D
up
of the corresponding labelling se-
quence is D
up
=
[x, y]
T
∈ R
2
| − 30 ≤ x ≤
+60, 5 ≤ y ≤ 30
. This choice guarantees that
the relation (1) is satisfied.
• Interpolation and data raw generation. The se-
quences of trends are interpolated to obtain a
unique sequence of fictitious prices values of a
stock.
In order to test the robustness of the classification sys-
tem we add some noise to the original sequences be-
fore the interpolation step. In particular we consider
two different types of noise:
• Intra Pattern. The noise is added in a frequent pat-
tern according to a probability µ. Three types of
intra pattern alterations are possible, deletion, in-
sertion or substitution of N
MAX
objects in each in-
stance of a pattern.
• Inter Pattern. This noise is used to insert noisy
objects between patterns in a sequence, randomly
generated in D. The parameter η defines the ratio
between the total duration of all the symbols in the
sequence and the total time of the sequence after
the insertion of noise. In formula
η =
size
seq
·t
pat
t
tot
in which t
tot
= size
seq
·t
pat
+ t
noise
.
4.2 Real Data Set Description
For experiments on real data we decide to try our
method on a inter-day trading task. Since for our pur-
pose we need to employ a financial time-series with
a high frequency sampling time we choose data sets
with a five minute tick. We decide to employ our
method on single stocks and on stock market index.
To this aim, we consider Lukoil, Gazprom, MICEX
and CAC-40, all in the time window from 1/1/2009 to
14/4/2014.
4.3 Classification Results
In order to test the performance of the classification
system we present three different types of synthetic
experiments: (1) clean sequence database (2) fixed
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
286

intra pattern noise with different degrees of inter pat-
tern noise, (3) fixed inter pattern noise with different
degrees of intra pattern noise. We generate N
pat
= 5
sequential patterns of mean length l
sec
= 8. The Train-
ing Set S
tr
is balanced (Possemato and Rizzi, 2013)
and contains 100 patterned sequences (50 sequences
per class) and 100 labeling sequences, while the Vali-
dation and Test Sets (S
vs
and S
ts
) contain 50 patterned
sequences (25 sequences per class) and 50 label-
ing sequences. The feature-based classifier adopted
on the embedding space is based on the k-NN rule
equipped with the Euclidean metric. The symbols
alphabet are extracted considering subsequences of
length between l
min
= 4 and l
max
= 11. The overall
GRASC-F performance measure is the generalization
capability achieved on S
ts
defined as follows:
Accuracy = 1−
#errS
ts
|S
ts
|
(3)
in which #errS
ts
is the number of classification er-
rors on the sequences of S
ts
. As shown in our pre-
vious work (Rizzi et al., 2013) the optimized sys-
tem parameters allow a better performance with re-
spect to default parameters. RL-GRADIS parame-
ters are defined in the following search intervals: Q ∈
{1, ··· , 300}, α ∈ [0, 0.1], β ∈ [0, 0.01], ε ∈ [0, 0.1],
and θ ∈ [0, 0.1]. The number of breakpoints for the
preprocessing procedure can vary in the interval bp ∈
[10, 100]. The number of iterations performed for
each optimization by GA is set to 10. We have empiri-
cally verified that the GA convergeto a stable solution
in less than 10 iterations. We show the results for k of
the k-NN rule fixed to 3. The genetic algorithm has
been initialized by proper random seeds.
4.3.1 Inter-Pattern Noise
The first experiments are performed setting µ = 0, i.e.
no intra-pattern noise, and increasing levels of inter
pattern noise η. This means that the patterns are left
unaltered, but increasing amounts of random objects
are added between symbols in every sequence. Note
that the smaller is the η parameter, the higher is the
inter-pattern noise and the longer is the duration of
the each sequence (both patterned and labelling). Re-
sults obtained are shown in Figure 4. The curve of
the classification accuracy shows a counterintuitive
trend. Higher amounts of inter-pattern noise (that
means lower values for the η parameter) indicate that
the frequent symbols are more likely to be separated
by random objects. This prevents the clustering algo-
rithm to find false patterns generated by portions of
real contiguous patterns. This behavior occurs until
the η parameter is higher than 0.3. After this value
the number of noisy objects becomes very high and it
is more difficult to identify frequent symbols signifi-
cant for the classification problem at hand.
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
55
60
65
70
75
80
85
90
95
100
105
Classification Accuracy on Test Set (µ = 0)
Accuracy
η
Figure 4: Classification Accuracy on Test Set considering
a fixed intra-pattern noise µ = 0 with respect to the level of
inter-pattern noise η.
4.3.2 Intra-Pattern Noise
Considering the results of previous experiments, in
these tests we set η = 0.7 and we progressively in-
crease the value of the intra-pattern noise µ. The clas-
sification accuracy is shown in Figure 5. The higher
is the intra-pattern noise, the lower is the classifica-
tion accuracy on the test set. As we could expect, the
generalization capability of the classification system
decreases with the increase of noisy patterns.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
65
70
75
80
85
90
Classification Accuracy on Test Set (η = 0.7)
Accuracy
µ
Figure 5: Classification Accuracy on Test Set considering a
fixed inter-pattern noise η = 0.7 with respect to the level of
intra-pattern noise µ.
4.3.3 Real Data Results
We perform tests on real data sets described in Sec-
tion 4.2. Table 1 shows the results in terms of clas-
sification error on the test set and of the number of
CombiningPiecewiseLinearRegressionandaGranularComputingFrameworkforFinancialTimeSeriesClassification
287

sequences of S
ts
before and after the reduction phase
described in Section 3.3. We can note that the over-
all number of selected sequences after the reduction
phase is higher for single stocks than for the stock
market indexes. Considering that the error rate be-
tween the stock market indexes and the single stocks
(apart from CAC-40) is very similar, we can say that
this is a very encouraging result because in principle,
if we perform this method on a big set of different
stocks, we could obtain a gain on average. From this
point of view, we consider very promising the per-
formances obtained on real stocks prices in this first
work.
Table 1: Results on Real Data Sets: Lukoil (L), Gazprom
(G), MICEX (M), CAC-40 (C). Classification Error on Test
Set, number of sequences in the Test Set and number of
selected sequences after the reduction procedure.
Err. S
ts
(%) # seq. S
ts
# sel. seq. S
ts
L 52.8571 202 63
G 54.2334 202 126
M 55.5556 202 13
C 100 208 1
5 CONCLUSION AND FUTURE
WORK
In this paper we introduce a new classification system
aiming to perform trend prediction on financial time
series. We prove, through synthetic benchmarking
data sets, that if there are some regularities inside data
our method is able to detect them, showing good clas-
sification performances also in the presence of noise
and with errors in the labeling procedure. The results
on real data show us the path to follow for the future
extension of the proposed method. We consider as en-
couraging the result obtained on real data, suggesting
further developments. To this aim, among other pos-
sible improvements, we are currently working on an
agent based mining algorithm, as the core procedure
for the alphabet synthesis.
REFERENCES
Bagheri, A., Mohammadi Peyhani, H., and Akbari, M.
(2014). Financial forecasting using anfis networks
with quantum-behaved particle swarm optimization.
41:6235–6250.
Bargiela, A. and Pedrycz, W. (2003). Granular computing:
an introduction. Springer.
Berndt, D. J. and Clifford, J. (1994). Using dynamic time
warping to find patterns in time series. In KDD work-
shop, volume 10, pages 359–370. Seattle, WA.
Chang, P.-C., Fan, C.-Y., and Liu, C.-H. (2009). Integrating
a piecewise linear representation method and a neu-
ral network model for stock trading points prediction.
Systems, Man, and Cybernetics, Part C: Applications
and Reviews, IEEE Transactions on, 39(1):80–92.
Cheng, C.-H., Su, C.-H., Chen, T.-L., and Chiang, H.-H.
(2010). Forecasting stock market based on price trend
and variation pattern. 5990:455–464.
Haugen, R. A. (1999). The new finance: the case against ef-
ficient markets, volume 2. Prentice Hall Upper Saddle
River.
Kendall, G. and Su, Y. (2005). A particle swarm optimi-
sation approach in the construction of optimal risky
portfolios. In Artificial Intelligence and Applications,
pages 140–145. Citeseer.
Livi, L., Del Vescovo, G., and Rizzi, A. (2012). Graph
recognition by seriation and frequent substructures
mining. In ICPRAM, pages 186–191.
Los, C. A. (2000). Nonparametric efficiency testing of asian
stock markets using weekly data. Advances in Econo-
metrics, 14:329–363.
Malkiel, B. G. and Fama, E. F. (1970). Efficient capital
markets: A review of theory and empirical work. The
journal of Finance, 25(2):383–417.
Muggeo, V. M. (2003). Estimating regression models
with unknown break-points. Statistics in medicine,
22(19):3055–3071.
Nanni, L. (2006). Multi-resolution subspace for financial
trading. Pattern recognition letters, 27(2):109–115.
Possemato, F. and Rizzi, A. (2013). Automatic text cate-
gorization by a granular computing approach: Facing
unbalanced data sets. In Neural Networks (IJCNN),
The 2013 International Joint Conference on, pages 1–
8. IEEE.
Radeerom, M., Wongsuwarn, H., and Kasemsan, M. L. K.
(2012). Intelligence decision trading systems for stock
index. 7198:366–375.
Rizzi, A., Del Vescovo, G., Livi, L., and Mascioli, F. M. F.
(2012). A new granular computing approach for se-
quences representation and classification. In Neural
Networks (IJCNN), The 2012 International Joint Con-
ference on, pages 1–8. IEEE.
Rizzi, A., Possemato, F., Livi, L., Sebastiani, A., Giuliani,
A., and Mascioli, F. M. F. (2013). A dissimilarity-
based classifier for generalized sequences by a gran-
ular computing approach. In Neural Networks
(IJCNN), The 2013 International Joint Conference on,
pages 1–8. IEEE.
Sai, Y., Yuan, Z., and Gao, K. (2007). Mining stock mar-
ket tendency by rs-based support vector machines. In
Granular Computing, 2007. GRC 2007. IEEE Inter-
national Conference on, pages 659–659. IEEE.
Vanstone, B. and Tan, C. (2003). A survey of the application
of soft computing to investment and financial trading.
Information Technology papers, page 13.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
288
