
Suppression of Building Vibrations
Using PD+PI Type Fuzzy Logic Controller
Yuksel Hacioglu
Department of Mechanical Engineering, Istanbul University, Avcilar, Istanbul, Turkey
Keywords: Building Vibrations, Fuzzy Logic Control, Earthquake Excitation.
Abstract: In order to bring the useful properties of PD and PI type fuzzy logic controllers together, a PD+PI type
fuzzy logic controller for vibration suppression of a building was presented in this study. The building has
nine storeys and an active tuned mass damper was placed on the top floor. The building model was excited
with a real earthquake ground motion. The results have shown that designed controller attenuated the
building vibrations successfully.
1 INTRODUCTION
During the last decades developing technology gave
rise to construction of high and slender buildings
and those tall buildings are more susceptible to
dangerous effects of earthquakes. This is why the
control of building vibrations is essential. In fact
suppressing the vibrations will result in increased
safety and comfort of occupants. The tuned mass
damper (TMD), which is an auxiliary mass
connected to the main body via a spring and a
damper, has been widely used (Ahlawat and
Ramaswamy, 2003). In recent years active tuned
mass dampers (ATMD) were also presented where
an actuator is placed generally parallel to the spring
and damper. Various control strategies have been
proposed with ATMD equipped buildings such as
LQR control (Fujita, 1994), fuzzy logic control
(Guclu and Yazici, 2008), H
∞
control (Poncela et al.,
2007) and backstepping control (Hacioglu and
Yagiz, 2012).
Fuzzy logic control, which is based on fuzzy set
theory presented by Zadeh (Zadeh, 1965), has
become popular within automatic control
community during the last years. This is mainly due
to the fact that it do not require the exact
mathematical model of the system and make
possible to use the knowledge in linguistic form
coming from the experts. Fuzzy logic control has
found different application areas such as active
vehicle suspension control (Yagiz et al., 2008),
robotic manipulator control (Yagiz and Hacioglu),
power systems control (Yesil et al., 2004) etc.
It is well known that classical fuzzy logic controller
namely PD type fuzzy controller can give rise to
steady state errors. On the other hand using PI type
fuzzy logic can solve this problem but with possible
poor transient performance. Therefore in this study a
PD+PI type fuzzy logic controller is designed for the
ATMD controlled nine storey building model.
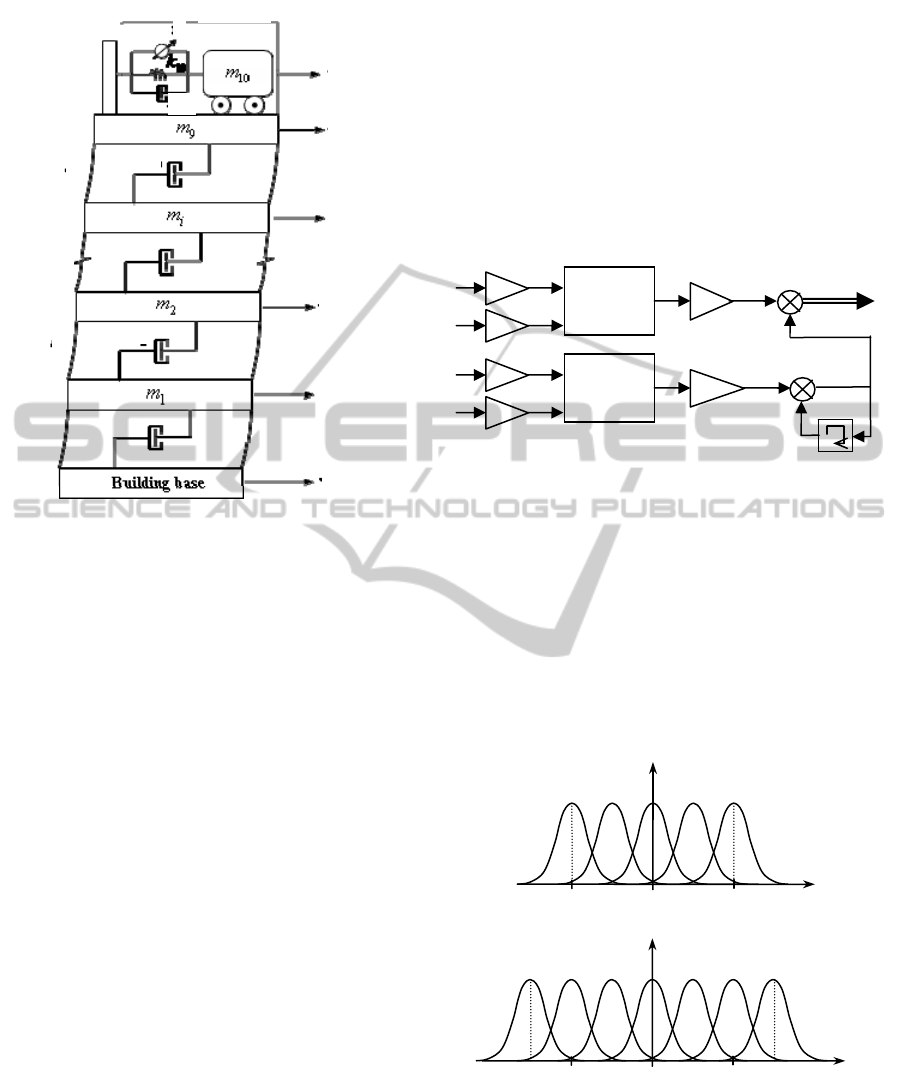
2 BUILDING MODEL
A nine storey building model as seen in Figure 1 is
used in this study. The ATMD is placed on top floor.
Here, m
i
, k
i
, b
i
, and y
i
(i=1,…,9) denote the mass,
stiffness, damping and lateral absolute displacement
of the related storey, respectively. Additionally, m
10
,
k
10
, b
10
and y
10
stand for the mass, stiffness, damping
and lateral absolute displacement of the ATMD,
respectively; u is the control force generated by the
actuator; y
0
is the earthquake ground motion input to
the building.
The equations of motion of the building model
are given below.
It should be noted that, in equations (1) – (10) if
u=0, then the equations of motion for the building
model with TMD is obtained. If in addition, m
10
=0,
k
10
=0 and b
10
=0 are set then, the equations of motion
for the building model without any auxiliary mass
are obtained.
153
Hacioglu Y..
Suppression of Building Vibrations Using PD+PI Type Fuzzy Logic Controller.
DOI: 10.5220/0005129101530157
In Proceedings of the International Conference on Fuzzy Computation Theory and Applications (FCTA-2014), pages 153-157
ISBN: 978-989-758-053-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
SF
1
e
N
e
SF
2
e
N
e
Fuzzy
Logic
Controlle
r
N
u
SF
u
PD
t
u
)
(
SF
3
e
N
e
SF
4
e
N
e
Fuzzy
Logic
Controlle
r
N
u
SF
Δu
PI
t
u
)
(
PI
t
u
)
(
PI
t
t
u
)
(
PI
PD
t
u
)
(
+
+ +
+
Figure 1: The building model.
11 1 1 0 2 2 1 1 1 0
22 1
0
my b y y b y y k y y
ky y
(1)
22 22 1 33 2 22 1
33 2
0
my b y y b y y k y y
ky y
(2)
33 3 3 2 4 4 3 3 3 2
44 3
0
my b y y b y y k y y
ky y
(3)
44 44 3 55 4 44 3
55 4
0
my b y y b y y k y y
ky y
(4)
55 55 4 66 5 55 4
66 5
0
my b y y b y y k y y
ky y
(5)
66 6 6 5 7 7 6 6 6 5
77 6
0
my b y y b y y k y y
ky y
(6)
77 77 6 88 7 77 6
88 7
0
my b y y b y y k y y
ky y
(7)
88 88 7 99 8 88 7
99 8
0
my b y y b y y k y y
ky y
(8)
99 99 8 1010 9 99 8
10 10 9
mybyybyykyy
ky y u
(9)
10 10 10 10 9 10 10 9
my b y y k y y u
(10)
3 CONTROLLER DESIGN
The PD+PI type fuzzy logic controller is presented
in this section. It consists of two parts as seen in
Figure 2, namely the PD and PI parts. The fuzzy
logic controllers use the error e
N
and its derivative
N
e
as inputs. The output of the PD-type fuzzy
controller is the control signal u
N
and the output of
the PI-type fuzzy logic controller is the incremental
change in control signal Δu
N
. Then the resultant
control law for the designed PD+PI controller is
given as
PIPIPDPIPD
ttutututu )()()()(
(11)
Figure 2: Structure of the controller.
As presented in Figure 3, Gaussian membership
functions all defined on the [-1,1] closed interval are
used for the input and output variables. Therefore
scaling factors (SF
i
: input scaling factors; SF
u
and
SF
(Δu)
: output scaling factors) are used in order to
map the crisp variables to their fuzzy counterparts.
For the membership functions used, NB, NM, NS, Z,
PS, PM and PB denote negative big, negative
medium, negative small, zero, positive small,
positive medium and positive big, respectively.
Figure 3: Membership functions for the input and output
variables.
The fuzzy rules are presented in Table 1 and they
were arranged in such a manner that the input
variables are forced to be zero. For example if error
-1
1
0
NB NM NS Z PS PM PB
μ(
u
N
, Δu
N
)
u
N
, Δu
N
N
e
,
N
e
-
1
1
0
NB NS Z PS PB
μ(
N
e
,
N
e
)
k
1
k
2
k
i
k
9
y
0
y
1
y
2
y
i
y
9
y
10
u
b
1
b
2
b
i
b
9
b
10
ATMD
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
154

is positive big (
e=PB) and derivative of error is zero
(
e
=Z) the control output variables are selected to be
positive medium (u
N
=PM and Δu
N
=PM). Similarly if
both inputs are zero, which is the desired case, then
the control outputs are selected to be zero (u
N
=Z and
Δu
N
=Z).
Table 1: Fuzzy rule table for u
N
and Δu
N
.
N
e
N
e
NB NS Z PS PB
NB
NB NB NM NS Z
NS
NB NM NS Z PS
Z
NM NS Z PS PM
PS
NS Z PS PM PB
PB
Z PS PM PB PB
4 NUMERICAL RESULTS
The numerical results for the nine storey building
model with PD+PI type fuzzy logic controlled
ATMD is presented in this section. The ground
motion in East-West direction of the Kocaeli
Earthquake in Turkey, which occurred on 17 August
1999, was applied to the base of the building model
as shown in Figure 4. The data used was recorded
during the main shock of that earthquake by the
station located in Besiktas, Istanbul, Turkey
(Acceleration data is available at the website of the
National Strong Motion Observation Network of
Turkey). Active and passive modes are introduced
for the ATMD. For small vibrations of the building,
the controller is inactive thus ATMD becomes TMD
and for large vibrations of the building the controller
is active thus TMD becomes ATMD. The average of
the absolute value of the top floor displacement
calculated over last Δt=2 s time period was used for
switching criterion.
0 20 40 60 80 100 120 140
-0.1
-0.05
0
0.05
0.1
t (s)
y
0
(m)
Figure 4: Earthquake ground motion.
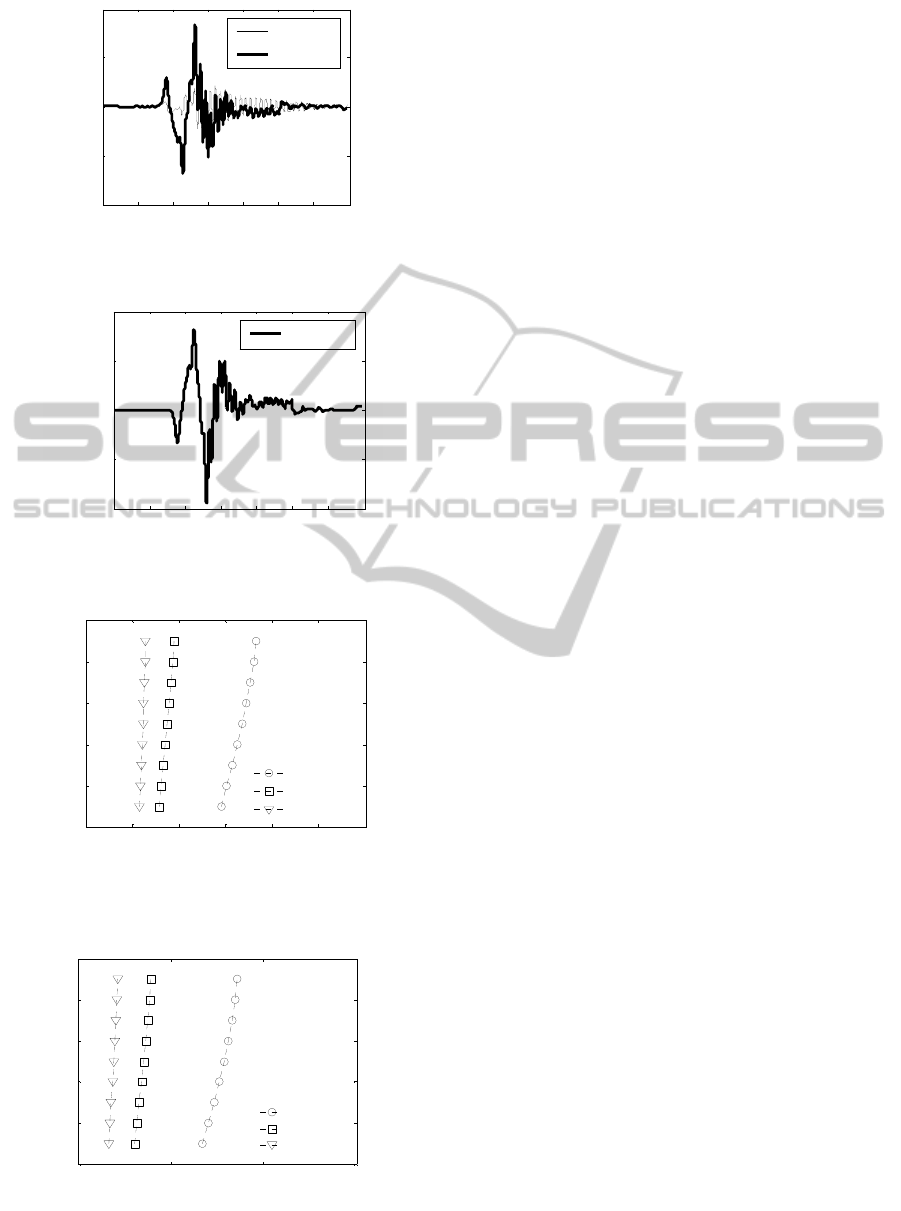
The displacements and accelerations of the top
floor are presented in Figure 5 and Figure 6 for the
building model without TMD or ATMD (which is
called Passive), with TMD and with designed fuzzy
logic controlled ATMD. It is observed from those
figures that both TMD and ATMD reduced the
building vibrations, and it is obvious that the fuzzy
logic controlled ATMD achieved better vibration
isolation than the TMD case.
0 20 40 60 80 100 120 140
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
t (s)
y
9
(m)
Passive
TMD
ATMD
Figure 5: Displacement of the top floor.
The displacements of the TMD and ATMD are
shown in Figure 7. It is seen that the ATMD moves
much more than the TMD while being in reasonable
ranges. Controller force for the ATMD case is also
given in Figure 8.
Finally, the RMS values of the displacements
and accelerations of the building floors are
calculated and presented in Figure 9 and Figure 10
for the passive, TMD and ATMD cases. It is clear
from those figures that the designed PD+PI type
fuzzy logic controlled ATMD reduced those RMS
values for displacements and accelerations much
more than the TMD case, which confirmed the
superior performance of the designed controller.
0 20 40 60 80 100 120 14
0
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
t (s)
y
9
(m/s
2
)
Passive
TMD
ATMD
..
Figure 6: Accelerations of the top floor.
SuppressionofBuildingVibrationsUsingPD+PITypeFuzzyLogicController
155
0 20 40 60 80 100 120 140
-0.8
-0.4
0
0.4
0.8
t
(
s
)
y
10
(m)
TMD
ATMD
Figure 7: Displacements of the TMD and ATMD.
0 20 40 60 80 100 120 140
-200
-100
0
100
200
t (s)
u (kN)
ATMD
Figure 8: The controller force.
0 0.02 0.04 0.06 0.08 0.1 0.12
0
2
4
6
8
10
"RMS" values of displacements
Fl
oor num
b
er
Passive
TMD
ATMD
Figure 9: RMS values for the displacements of the all
floors.
0 0.2 0.4 0.6
0
2
4
6
8
10
"RMS" values of accelerations
Floor number
Passive
TMD
ATMD
Figure 10: RMS values for the accelerations of the all
floors.
5 CONCLUSIONS
In order to suppress the earthquake induced
vibrations of a nine storey building, a PD+PI fuzzy
logic controller was designed. The controller was
applied through an active tuned mass damper
installed on the top floor of the building. The results
indicated that the designed controller has attenuated
the vibrations of the building floors to a certain
degree.
REFERENCES
Ahlawat, A.S. and Ramaswamy A, 2003. Multiobjective
optimal absorber system for torsionally coupled
seismically excited structures. Engineering Structures
25(7), 941-950.
Fujita, T., 1994. Application of hybrid mass damper with
convertible active and passive modes using hydraulic
actuator to high-rise building. Proceedings of the
American Control Conference, Baltimore, Maryland,
June 29 - July 1, Vol. 1, 1067-1072.
Guclu, R. and Yazici, H., 2008. Vibration control of a
structure with ATMD against earthquake using fuzzy
logic controllers. Journal of Sound and Vibration
318(1-2), 36-49.
Hacioglu, Y., Yagiz, N., 2012. Adaptive backstepping
control with estimation for the vibration isolation of
buildings, Journal of Vibration and Control, 18(13),
1996-2005.
National Strong Motion Observation Network of Turkey.
Available at: http://kyh.deprem.gov.tr
Poncela A., Casado C., Baeyens E. and Peran J.R., 2007.
Design of devices for protecting civil structures using
fixed-order control. Structural Control and Health
Monitoring 14(2), 239-260.
Yagiz, N., Hacioglu, Y., 2005. Fuzzy sliding modes with
moving surface for the robust control of a planar robot,
Journal of Vibration and Control, 11(7), 903-922.
Yagiz, N., Hacioglu, Y., Taskin, Y., 2008. Fuzzy sliding-
mode control of active suspensions, IEEE
Transactions on Industrial Electronics, 55(11), 3883-
3890.
Yesil, E., Guzelkaya, M., Eksin, I., 2004. Self tuning
fuzzy PID type load and frequency controller, Energy
Conversion and Management, 45, 377-390.
Zadeh, L.A. 1965. Fuzzy Sets, Information and Control, 8,
338-353.
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
156

APPENDIX
Table A1: Numerical values of the parameters of the
building model.
Parameter Value
3
10
kg
m
1
450
m
2
345
m
3
345
m
4
345
m
5
345
m
6
345
m
7
345
m
8
345
m
9
345
m
10
69
Parameter Value
6
10
N/m
k
1
18.05
k
2
340
k
3
326
k
4
285
k
5
269
k
6
243
k
7
207
k
8
169
k
9
137
k
10
0.3365
Parameter Value
3
10
N s/m
b
1
26.17
b
2
490
b
3
467
b
4
410
b
5
386
b
6
348
b
7
298
b
8
243
b
9
196
b
10
152.39
Table A2: Numerical values of the parameters of the
controller.
Parameter Value
SF
1
1.5
SF
2
1
SF
3
1.5
SF
4
1
SF
u
200000
SF
Δu
4000
SuppressionofBuildingVibrationsUsingPD+PITypeFuzzyLogicController
157
