A New Adaptive Universal Fuzzy Inference System with Application
Yuan Yuan Chai
1
, Jun Chen
1
, Wei Luo
1
and Li Min Jia
2
1
Network Center, China Defense Science and Technology Information Center, Fucheng Road 26#, Beijing, China
2
State Key Lab of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing, China
Keywords: Fuzzy Inference System, Adaptive Universal Fuzzy Inference System, Choquet Integral-OWA Operator
based Fuzzy Inference System, Choquet Integral-OWA Operator based Adaptive Universal Fuzzy Inference
System.
Abstract: Through comprehensive study on existing fuzzy inference systems, this paper presents a Choquet integral-
OWA operator based fuzzy inference system (AggFIS) in order to solve the traditional FIS disadvantages
and its adaptive model which is named Choquet integral-OWA operator based adaptive universal fuzzy
inference system (Agg-AUFIS). By considering the universal fuzzy inference operators and importance
factor during reasoning process, Agg-AUFIS tries to express the essence of fuzzy logic and simulate human
thinking pattern sufficiently, which could provide a new methodology for fuzzy modeling in future.
1 INTRODUCTION
Fuzzy sets theory (linguistic variable) was
introduced by Zadeh in 1965 as a new modeling
technique based on human knowledge and thinking
pattern (Zadeh, 1965), which has gained an
increasing level of acceptance in science and
engineering. Hybrid tools which are developed by
using combinations of fuzzy logic and neural
networks require relatively short development times
and are robust. Through understanding fuzzy logic
essence and various adaptive fuzzy inference
systems, this paper presents a Choquet integral-
OWA operator based fuzzy inference system
(AggFIS) and its adaptive model named as Choquet
integral-OWA operator based adaptive universal
fuzzy inference system (Agg-AUFIS), which are
tested by historical sample data of traffic flow.
2 FUZZY MODELING
When the application domain moves from simple
systems to complex ones, the usual operation
procedure becomes infeasible and we need the
intelligent and adaptive methods to solve all these
problems. System modeling based on conventional
mathematical tools (e.g., differential equations) is
not well suited for dealing with ill-defined and
uncertain systems. By contrast, a fuzzy model of a
system (or a fuzzy inference system) employing
expert knowledge and fuzzy if-then rules can model
the qualitative aspects of human reasoning processes
without implementing precise quantitative analysis.
2.1 Fuzzy Model of a System
The introduction of fuzzy sets can express the
human thinking pattern with relatively simple
mathematics format so that it is "intelligent" and
possible to handle complex nonlinear problems
consistent with the human mind (Zadeh, 1973).
Fuzzy logic aims at modeling the imprecise modes
of reasoning that play an essential role in the
remarkable human ability to make rational decisions
in an environment of uncertainty and imprecision.
This ability depends on our ability to infer an
approximate answer to a question based on a store of
knowledge that is inexact, incomplete, or not totally
reliable (Zadeh, 1988).
Recent interest has developed in the use of fuzzy
set theory for modeling of complex systems. We call
such a representation a fuzzy model of a system
(FMS). Fuzzy modeling based on fuzzy inference is
used to describe the model of the object using fuzzy
if-then rules and aims at constructing a mathematics
paradigm of linguistic analysis for complex system
or progress, which can transform nature language
into algorithm language that can be handled by
computer (Pedrycz et al., 1995; Pedrycz and
Oliveira, 1996). Once a model is identified, it can be
163
Chai Y., Chen J., Luo W. and Jia L..
A New Adaptive Universal Fuzzy Inference System with Application.
DOI: 10.5220/0005130501630168
In Proceedings of the International Conference on Fuzzy Computation Theory and Applications (FCTA-2014), pages 163-168
ISBN: 978-989-758-053-6
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

applied to analysis, prediction, control, diagnosis of
the object.
Comparing with the traditional mathematics
modeling, a fuzzy model of a system (or a fuzzy
inference system), which is established according to
fuzzy set theory and fuzzy logic, implements a non-
linear mapping from its input space to output space
by simulating human thinking mode. The Stone-
Weierstrass theorem indicates that a fuzzy inference
system (FIS) can approximate arbitrary nonlinear
function (Zadeh, 1994), the reasoning process of
which is shown in Figure 1.
Figure 1: Reasoning process of fuzzy inference system.
Conceptually a fuzzy logic controller or more
generally any FMS can be also seen as a function f
mapping input to output. See in Figure 2.
Figure 2: Nonlinear mapping model of FMS.
Essentially f can be seen as a mapping f : X→Y,
y = f(x), where X and Y are the base sets of U and V
respectively (U and V are fuzzy sets of X and Y).
Formally we can represent this mapping as a
relationship F on X*Y such that (x, y)∈F, if f(x) = y
(Yager, 1993a). It is also reported that a fuzzy
inference system (FIS) is a universal approximator
(Furuhashi, 2001).
Fuzzy modeling is an iterative progress and
knowledge is the reasoning cores which make the
output improve continually. It is concluded that
FMS (or FIS) could be an intelligent modeling
method because of its reasoning ability and
nonlinear mapping function.
2.2 Some Shortcomings of FIS
According to fuzzy reasoning type and format of
fuzzy if-then rules, most FIS can be divided into
three classes: Mamdani fuzzy inference system,
Sugeno fuzzy inference system and Tsukamoto
fuzzy inference system.
T-S fuzzy inference system works well with
linear techniques and guarantees continuity of the
output surface. The consequent of each rule is a
linear combination of input variables rather than
membership functions and each rule has a crisp
output. But T-S fuzzy inference system has
difficulties in dealing with the multi-parameter
synthetic evaluation and in assigning weight to each
input and fuzzy rule.
Mamdani fuzzy inference system has some
advantages superior to T-S system (Mamdani, 1977;
Esragh and Mamdani, 1981):
 It’s intuitive;
 It has widespread acceptance;
 It’s well-suited to human cognition and reflects
the nature of fuzzy logic.
Mamdani model can show its legibility and
understandability to the laypeople and has
advantages in consequent expression and intuitive
reasoning, which is applied in many practical
problems. M-FIS does well in solving multi-
parameter evaluation problems, but it needs large
calculation amount for defuzzification and it also has
difficulties in weight expression.
So we conclude that there are the following two
major disadvantages in the existing FIS:
(1) In the existing fuzzy inference systems, the
choice of fuzzy inference operators is relatively
fixed and reasoning composite method is also
limited to two methods, such as Max-min and Sum-
product. For example, in MATLAB fuzzy logic
toolbox, the choice of AND operator is only Product
or Min and the output of FIS is calculated by using
the given operators. The commonly used fuzzy
inference operators and reasoning composite
methods may make us more and more limited in
understanding nature of FIS.
The essence of fuzzy inference system is a non-
linear mapping and each step of fuzzy reasoning is
also a non-linear mapping process. From this point
of view, other reasoning operators could be used to
achieve each reasoning step of FIS in addition to
traditional inference operators and we should have a
comprehensive understanding of fuzzy inference
system.
(2) In traditional fuzzy inference systems,
importance (weight) of each input and each rule is
not considered, which means their contribution to
the overall output is same during the reasoning. This
inference process is not consistent with human
cognition. For example, when we want to buy a bus,
price is most important factor to be considered first,
followed by comfort, colour, etc.
Therefore, considering the importance (weight) of
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
164

each criterion (input or rule) will make FIS more
close to human thinking manner and reflect the
nature of fuzzy logic better.
In order to solve these shortcomings and
limitations, we need a "universal" fuzzy inference
system, which could:
 use the universal fuzzy inference operators and
replace the existing traditional operators to
realize the reasoning process;
 consider the importance factor of objects (inputs
and rules) and establish the inference model that
could completely represent fuzzy logic essence
and simulate human thinking pattern.
This paper introduces a Choquet integral-OWA
operator based fuzzy inference system known as
AggFIS, which is a more "universal" fuzzy inference
system, and its adaptive model respectively in next
chapters.
3 CHOQUET INTEGRAL-OWA
OPERATOR BASED FUZZY
INFERENCE SYSTEM
Fuzzy inference is a computer paradigm based on
fuzzy set theory, fuzzy if-then-rules and fuzzy
reasoning. The basic structure of fuzzy inference
system mainly consists of three parts: rule base
which contains the set of fuzzy rules; database (or
dictionary) which defines the membership functions
used in the fuzzy rules; a reasoning mechanism
which performs the inference procedure to derive a
conclusion from facts and rules.
3.1 Fuzzy Inference Operator
To completely specify the operation of a fuzzy
inference system, we need to assign a function for
each of the following operators:
 AND operator (usually T-norm) for calculating
the rule firing strength with AND'ed antecedents
 OR operator (usually T-conorm) for calculating
the rule firing strength with OR'ed antecedents
 Implication operator (usually T-norm) for
calculating qualified consequent MFs based on
given firing strength
 Aggregate operator (usually T-conorm) for
aggregating qualified consequent MFs to
generate an overall output MF
 Defuzzification operator for transforming an
output MF to a crisp single output value
Once the above five kinds of operators are
determined, we have identified one fuzzy inference
system (FIS). According to the fuzzy inference
operators, FIS can be generally divided into five
layers:
The first layer is fuzzification layer, which is
used to make crisp input fuzzification and the degree
of compatibility is based on antecedent MF; the fifth
layer is defuzzification layer, which extracts a crisp
value that best represents a fuzzy set from overall
MFs. There are five methods for defuzzifying a
fuzzy set A of a universe of discourse Z and the
centroid of area (COA) is the most popular one
(Yager and Filev, 1992).
The second layer is the inference layer or rule
layer, which is used to calculate degree of the fuzzy
rule fulfilment (firing strength) corresponding to the
above AND or OR operator;
The third layer is the implication layer, which is
used to represent how the firing strength gets
propagated or used in a fuzzy implication statement
corresponding to the above implication operator;
The fourth layer is the aggregation layer, which
is used to aggregate all the qualified consequent
MFs to obtain an overall output MF corresponding
to the above aggregate operator.
In the case of crisp inputs and outputs, FIS
implements a nonlinear mapping from its input
space to output space. This mapping is completed by
a group of fuzzy if-then rules. We can assume that
each rule describes the local mapping behaviour.
Fuzzy rules are used to obtain inaccurate
information and expressed as inaccurate (natural
language) reasoning model, which makes FIS have
reasoning abilities similar to human mind under the
imprecise and uncertain environment.
3.2 AggFIS
This paper presents a Choquet integral-OWA
operator based fuzzy inference system named as
AggFIS, which uses the Choquet integral-OWA
operator composite method instead of T-conorm-T-
norm composite and COA defuzzification method in
reasoning process.
In the inference layer, we apply OWA operator
which replaces AND (OR) operator to calculate
firing strength (Yager, 1988, 1993b); in the
aggregation layer, we use Choquet integral instead
of the traditional T-conorm operator (Sum or Max)
to aggregate the qualified MFs and generate an
overall output MF (Grabisch, 2000); and the
defuzzification operator is centroid of area (COA).
Furthermore, in the reasoning process we assign
weight to each input, expressed by μ
i
; we also assign
weight to each rule, expressed by τ
i
.
ANewAdaptiveUniversalFuzzyInferenceSystemwithApplication
165

If we regard these FIS steps as aggregation
process, the replaced operators can be expressed as
"Agg" and we call this model "AggFIS".
Corresponding to different choice of each "Agg"
operator, we can get the different special FIS cases
(Kelman and Yager, 1995; Yager, 1996).
The reasoning process of AggFIS is shown in
Figure 3.
V
1
V
3 V
2
A
n
A
1
B
n
B
1
C
n
C
1
Agg Agg
D
n
D
1
Agg
D
u
1
u
1
u
2 u
2
u
3
u
3
U
D
-1
D
1
(x) D
n
(x)
a
1
,b
1
a
n
,b
n
τ
1
τ
n
Figure 3: Choquet integral-OWA operator based FIS.
The format of fuzzy rule is as follows:
If V
1
is A
1
and V
2
is B
1
and V
3
is C
1
, Then U is D
1
;
V
1
, V
2
, V
3
are the crisp inputs, U is the single
crisp output; A
1
, B
1
, C
1
represents the membership
function of each input variable; D
1
represents the
membership function of output variable. Where,
 D: membership function for the antecedents
(membership neural module);
 D
-1
: membership function for the consequents
(inverse membership neural module);
 D
i
(x): firing strength of each rule;
 µ
i
: importance (weight) of each input;
 τ
i
: importance (weight) of each rule;
 [a
i
, b
i
]: range value for each rule's output.
AggFIS has advantages in universal expression
of fuzzy inference operators and importance factor
of each criterion, which is trying to reflect fuzzy
logic essence and simulate human thinking pattern.
4 CHOQUET INTEGRAL-OWA
OPERATOR BASED ADAPTIVE
UNIVERSAL FUZZY
INFERENCE SYSTEM
A "universal" fuzzy inference system, which has the
universal fuzzy inference operators and considers
the importance factor during reasoning process, can
be transformed into the general structure of fuzzy
neural network by combining with feedforward
neural network. Such model has the capability of
learning and we call it as "adaptive universal fuzzy
inference system (AUFIS)". Through training, the
parameters in this model can be adjusted and it is
easy to extract fuzzy rules that described I/O
relationships of a nonlinear system from the trained
AUFIS.
If Choquet integral-OWA operator based fuzzy
inference system (AggFIS) is incorporated into a
feedforward neural network according to the above
theory, we obtain the adaptive model for AggFIS,
which is known as Choquet integral-OWA operator
based adaptive universal fuzzy inference system
(Agg-AUFIS).
In AggFIS, we choose the differentiable fuzzy
inference operators which ensure the reasoning
process continuity so that Agg-AUFIS has the ability
of learning and the adaptability to the data.
In this section, we first put forward the model
structure of Choquet integral-OWA operator based
adaptive universal fuzzy inference system (Agg-
AUFIS) and then discuss the learning rules for it.
4.1 Model Description
We assume Agg-AUFIS under consideration has
two inputs x and y and one output f. Suppose that
the rule base contains two fuzzy if-then rules:
Rule 1: If x is A
1
and y is B
1
, Then f is C
1
;
Rule 2: If x is A
2
and y is B
2
, Then f is C
2
.
Agg-AUFIS model consists of five layers which
is shown in Figure 4, output of each layer is as
following.
Figure 4: Agg-AUFIS model.
Layer 1: fuzzification layer:
Generate the membership grades µ
a
, µ
b
O
,

μ


 i=1,2 or
O
,

μ




 i=3,4
(1)
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
166

The membership function is the generalized bell
function:
μ


 
1
1
  










(2)
Where {a
i
, b
i
, c
i
} is the parameter set which
refers to premise parameters.
Layer 2: inference layer or rule layer:
O
,
ω

μ

 μ

 μ


  μ

 μ

 μ





i=1,2
(3)
Generate ω
1
, ω
2
by OWA operator, where µ
i
indicates the importance (weight) of each input.
Layer 3: implication layer:
O
,
ω

∘

i=1,2
(4)
Implication operator is product. The consequent
parameters are determined by Ci.
Layer 4: aggregation layer:
O


∑
ω

∘

ω

∘

τ

i=1,2 (5)
Aggregation operator is Choquet integral, where
τ
i
indicates the importance (weight) of each rule.
Layer 5: defuzzification layer
O



∘O

(6)
Compute the crisp output f. The defuzzification
method is COA (center of area).
In Agg-AUFIS, the parameters that need to be
adjusted include:
(1) Premise parameters: A
1
, A
2
, B
1
, B
2
represent
the premise parameters. The type of the inputs
membership functions (MF) is generalized bell
functions, each MF has 3 nonlinear parameters. The
total number of premise parameters is 12.
(2) Consequent parameters: C
1
, C
2
represent the
consequent parameters. If the consequent MF is
trapezoidal membership function, each MF has 4
nonlinear parameters to be adjusted. The total
number is 8.
(3) µ
i
: importance (weight) of each input. Total
number is 2.
(4) τ
i
: importance (weight) of each rule. Total
number is 2.
Total nonlinear parameters in this example are
24 which can be adjusted according to the parameter
updating formula discussed in the following.
4.2 Learning Rules for Agg-AUFIS
In this section, we conclude the learning rules for
Agg-AUFIS based on main idea of back propagation
(BP) in NN through discussing the general weight
updating formula in detail, which could provide a
theoretical reference for further study of learning
rules in adaptive fuzzy inference system (Rumelhart
et al., 1986; Rumelhart, 1994).
As the name implied, an adaptive FIS is a
network structure, the overall input-output behaviour
of which is determined by a collection of modifiable
parameters. A feedforward adaptive FIS is a
mapping between its inputs and output spaces. Our
goal is to construct a network for achieving a desired
nonlinear mapping which is regulated by a data set
consisting of desired input-output pairs of a target
system to be modeled: this data set is called training
data set. The procedures that adjust the parameters to
improve the network’s performance are called the
learning rules that explain how these parameters (or
weights) should be updated to minimize a predefined
error measure.
The basic idea of BP is to define a measure of
the overall performance of the system and then to
find a way to optimize that performance. The error
measure computes the discrepancy between the
network’s actual output and a desired output. We
then obtain the learning rules by putting a specific
optimization technique on the error measure. The
steepest descent method is used as a basic learning
rule. It is also called back propagation because the
gradient vector is calculated in the direction opposite
to the flow of the each node output.
We change the parameters of the system in
proportion to the derivative of the error with respect
to the weights. This simple procedure works
remarkably well on a wide variety of problems. A
key advantage of neural network systems is that
these simple, yet powerful learning procedures can
be defined, allowing the systems to adapt to their
environments.
In Agg-AUFIS model, we use back propagation
as the basic learning rule which means using
gradient vector in steepest descent method to update
all the nonlinear parameters. Once the gradient is
computed, regression techniques are used to update
parameters in the model and we conclude the
parameters updating formula for Agg-AUFIS as
follows:
ω


ω

∆ω

∆ω


η
∙
∂E
∂ω


η
∙
∂E
∂

∙
∂


∂ω


η
ε

∙
∂


∂ω

(7)
j<i, that is x

f


∑
ω

.x

θ, f
i
and x
i
means the
activation function and output of node i. Error signal
ε
i
, which can be derived by the previous layer nodes,
starts from the output layer and goes backward until
the input layer is attained.
The general parameters updating formula is:
ω


ω

η∙



∙

∙
(8)
ANewAdaptiveUniversalFuzzyInferenceSystemwithApplication
167

Where, η is the learning step, d
i
is the desired
output for node i, x
i
is the real output for node i, x
j
is
the input for node i, X is a Polynomial, which is:


1


(9)
5 EXPERIMENTS
In order to verify the validity of Choquet integral-
OWA operator based Adaptive Universal Fuzzy
Inference System (Agg-AUFIS) presented in this
paper, we established Agg-AUFIS for evaluation of
traffic level of service, which are trained and tested
by historical sample data (1429 pairs for training and
640 pairs for testing).
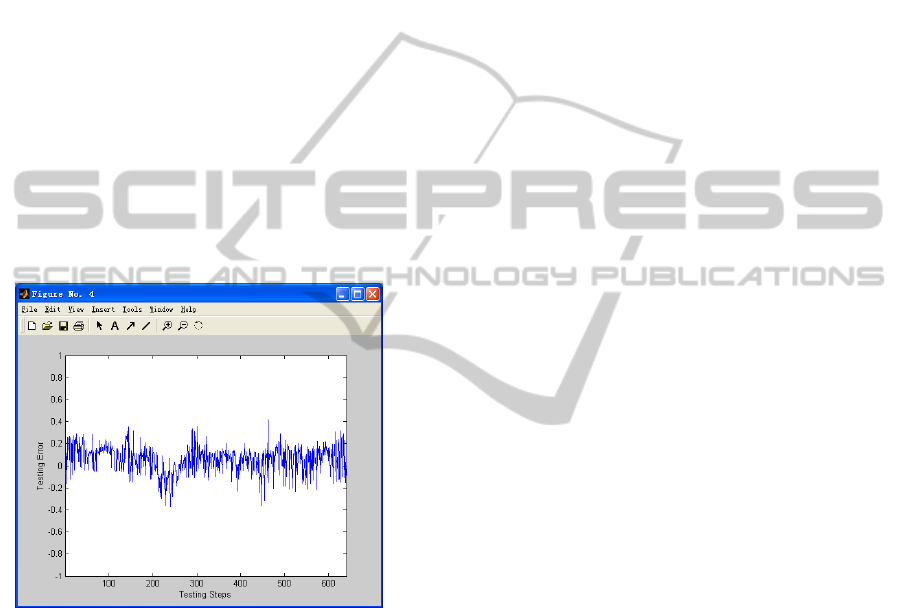
Testing errors are shown in Figure 5. Average
test error is 0.057391. The worst test error is 0.4154
while the best test error is 1.6785e-005. The results
indicated that Agg-AUFIS could be well adapted to
sample data and it is a kind of universal
approximator.
Figure 5: Testing error.
6 CONCLUSIONS
Based on FIS capability of simulating human
reasoning process and dealing with nonlinear system
problems, this paper presents a Choquet integral-
OWA operator based fuzzy inference system
(AggFIS) that is universal in reasoning operator
selection, inference model structure and importance
factor expression, and its adaptive model known as
Agg-AUFIS. The experiments results showed that
Agg-AUFIS has great non-linear mapping function
and complex system modeling capacity. The
comparative experiments will be made between
Agg-AUFIS and existing similar systems, which
could verify the advantages and effectiveness of
proposed model in future work.
REFERENCES
Esragh, F., Mamdani, E. H., 1981. A general approach to
linguistic approximation. Fuzzy Reasoning and Its
Applications, Academic Press. London.
Furuhashi, T., 2001. Fusion of fuzzy/neuro/evolutionary
computing for knowledge acquisition. Proceedings of
IEEE, 89(9), 1266-1274.
Grabisch, M., 2000. A Graphical Interpretation of the
Choquet Integral. IEEE transactions on Fuzzy
Systems, 8(5), 627-631.
Kelman, A., Yager, R. R., 1995. On the Application of a
Class of MICA Operators. International Journal of
Uncertainty, Fuzziness and Knowledge-Based
Systems, 3,113-125.
Mamdani, E. H., 1977. Application of Fuzzy Logic to
Approximate Reasoning Using Linguistic Synthesis.
IEEE transactions on computer, 26(12), 1182-1191.
Pedrycz, W., Lam, P., Rocha, A. F., 1995. Distributed
fuzzy system modeling. IEEE transactions on fuzzy
systems, man, and cybernetics, 25(5), 769-780.
Pedrycz, W., Oliveira, J., 1996. Optimization of fuzzy
models. IEEE transactions on fuzzy systems, man, and
cybernetics -PART B: cybernetics, 26(4), 627-636.
Rumelhart, D. E., Hinton, G. E., Williams, R. J., 1986.
Learning internal representations by error
propagation. Parallel distributed processing:
explorations in the microstructure of cognition, MIT
Press. Cambridge.
Rumelhart, D. E., 1994. The Basic Ideas in Neural
Networks. Communications of the ACM, 37(3), 87-92.
Yager, R. R., 1988. On Ordered Weighted Averaging
Aggregation Operators in Multicriteria
Decisionmaking. IEEE transactions on fuzzy systems,
man, and cybernetics, 18(1),183-190.
Yager, R. R., Filev, D. P., 1992. SLIDE:A simple adaptive
defuzzification method. IEEE transactions on Fuzzy
Systems, 1(1), 69-78.
Yager, R. R., 1993a. On a Hierarchical Structure for Fuzzy
Modeling and Control. IEEE transactions on fuzzy
systems, man, and cybernetics, 23(4), 1189-1197.
Yager, R. R., 1993b. Families of OWA operators. Fuzzy
Sets and Systems, 59, 125-148.
Yager, R. R., 1996. On Mean Type Aggregation. IEEE
transactions on fuzzy systems, man, and cybernetics -
PART B: cybernetics, 26(2), 209-221.
Zadeh, L. A., 1965. Fuzzy Set. Information and Control, 8,
338-353.
Zadeh, L. A., 1973. Outline of a New Approach to the
Analysis of Complex Systems and Decision Processes.
IEEE Transactions on Systems, Man, and Cybernetics,
3(1), 28-44.
Zadeh, L. A., 1988. Fuzzy Logic. Computer, 21(4), 83-93.
Zadeh, L. A., 1994. Soft Computing and Fuzzy Logic.
IEEE Software, 11(6), 48-56.
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
168