
Trawl-door Shape Optimization with 3D CFD
Models and Local Surrogates
Elvar Hermannsson
1
, Leifur Leifsson
2
, Slawomir Koziel
2
, Piotr Kurgan
2
and Adrian Bekasiewicz
3
1
KTH Royal Institute of Technology, School of Engineering Sciences, Stockholm, Sweden
2
Engineering Optimization & Modeling Center, Reykjavik University, Menntavegur 1, Reykjavik, Iceland
3
Faculty of Electronics, Telecommunications and Informatics, Gdansk University of Technology, 80-233 Gdansk, Poland
Keywords: Trawl-Door, Ship Fuel Efficiency, Hydrodynamics, Shape Optimization, 3D CFD.
Abstract: Design and optimization of trawl-doors are key factors in minimizing the fuel consumption of fishing
vessels. This paper discusses optimization of the trawl-door shapes using high-fidelity 3D computational
fluid dynamic (CFD) models. The accurate 3D CFD models are computationally expensive and, therefore,
the direct use of traditional optimization algorithms, which often require a large number of evaluations, may
be prohibitive. The design approach presented here is a variation of sequential approximate optimization
exploiting low-order local response surface models of the expensive 3D CFD simulations. The algorithm is
applied to the design of modern and airfoil-shaped trawl-doors.
1 INTRODUCTION
Trawling gear contributes to a majority of the
fuel expenditure of many fishing vessels. Fishing
gear main parts are the net, a pair of trawl-doors, and
a cable extending from the trawl-doors to the boat
and the net (see Fig. 1(a)). The role of the trawl-
doors is to keep the net open during the trawling
operation. Typically, their span is 6-8 m and chord
2-3 m, while the cables are over a few hundred
meters long and the net tens of meters. Figure 1(b)
shows a modern trawl-door. The trawl-doors may be
responsible for roughly 10-30% of the total drag of
the entire assembly (Garner, 1967). Good trawl-door
designs are therefore desired to minimize fuel
consumption.
In general, trawl-doors have remained the same
for many decades. This is mainly due to the fact that
their designs are based on time-consuming and
expensive physical experiments in tow- or flume
tanks. Computational fluid dynamics (CFD) is
widely used for the design of a variety of vehicles.
However, very few CFD-based studies are reported
for trawl-doors in the literature (Haraldsson, 1996).
Recently, a design optimization approach for
trawl-doors using 2D CFD models has been
introduced (Leifsson et al., 2014). The approach can
be categorized as surrogate-based. As a surrogate
model (i.e., a cheaper representation of expensive
CFD simulations) it exploits low-order local
response surface approximations of the sparsely
sampled 2D CFD simulation data.
(a)
(b)
Figure 1: Schematic of a fishing vessel with trawling gear
illustrating (a) the main parts of the fishing gear (not
drawn to scale), and (b) a typical trawl-door with two
slats.
Trawl-doors
Cables
Net
V
L
L
D
D
Main Element (ME)
cʹ
b
Slat 1
Slat 2
775
Hermannsson E., Leifsson L., Koziel S., Kurgan P. and Bekasiewicz A..
Trawl-door Shape Optimization with 3D CFD Models and Local Surrogates.
DOI: 10.5220/0005131307750784
In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SDDOM-2014), pages
775-784
ISBN: 978-989-758-038-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2D CFD models are a simplified representation
of the flow past trawl-doors. To perform a more
realistic and practical design of trawl-doors, 3D
CFD models are required to capture the flow physics
more accurately. In particular, the trawl-doors are
low aspect ratio, and, therefore, the tip vortex will
have significant effect on the overall performance.
In this paper, we extend our methodology to use 3D
CFD models, using the optimized 2D design as a
starting point. Although computationally more
expensive, the use of 3D CFD simulations turns out
to be critical for design reliability.
2 PROBLEM FORMULATION
The design goal is to optimize the shape and
configuration of trawl-doors. The design of other
components of the trawling gear is not considered here.
We setup the trawl-doors using a typical modern shape
(Fig. 2(a)) and with airfoil profiles (Fig. 2(b)) as
proposed in our earlier work (Jonsson et al., 2012;
Jonsson et al., 2013).
The objective is to minimize the drag of the 3D
trawl-door while maintaining a given lift to ensure
sufficient opening of the net. In particular, the
optimization problem is formulated as
min
(1)
subject to
∗
(2)
where C
D
the drag coefficient (a nondimensional form
of the trawl-door drag), C
D
is the lift coefficient, and
C
L
*
is the minimum allowable lift coefficient.
The position and inclination of the elements are the
design parameters. The design variable vector can be
written as
/ /
(3)
where x/c is the slat leading-edge position on the x-axis,
y/c is the slat leading-edge position on the y-axis,
is
the slat inclination relative to the x-axis,
is the flow
angle of attack relative to the x-axis, and c is the length
of the main element (c = 1 in this study). Upper and
lower bounds, u and l, respectively, are prescribed on
the design variables.
The size and shape of the elements is fixed. The
operating condition, the flow speed V
, is also fixed
during the optimization.
(a)
(b)
Figure 2: Section cuts of the two shapes, (a) a typical
modern trawl-door with thin elements (the F11), and (b) a
novel trawl-door with airfoil shaped elements.
3 CFD MODELS
This section describes the CFD models used in this
study. In particular, we describe the 2D and the 3D
CFD model setup and configuration, as well as give
the results of mesh convergence studies and model
validation.
3.1 Governing Equations
The flow is assumed steady, incompressible, and
viscous. The Reynolds-averaged Navier-Stoke
(RANS) equations are taken to be the governing
equations with Menter’s k-
SST turbulence model
(see, e.g., Tannehill et al., 1997).
3.2 Computational Grid
The farfield is configured in a box-topology where
the trawl-door geometry is placed in the center of the
box. The main element leading edge (LE) is placed
as the origin, with the farfield extending 100 chord
lengths away from the origin in every direction.
Figure 3 shows the 2D solution domain and Fig. 4
shows the 3D one.
The grid is an unstructured triangular one where
the elements are clustered around the trawl-door
geometry, growing in size as they move away from
the origin. The maximum element size on the
geometry is set to 0.1% of the chord length. The
maximum element size in domain away from the
trawl-door is 10 times the chord length. In order to
capture the viscous boundary layer well, a prismatic
inflation layer is extruded from all surfaces. The
initial layer height is chosen so that y
+
< 1. The mesh
is generated with ICEM CFD (ICEM CFD, 2012).
Example meshes is shown in Figs. 5 and 6.
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
776

Figure 3: 2D CFD model solution domain.
Figure 4: 3D CFD model solution domain.
(a) (b)
Figure 5: An example 2D computational grid, (a) the
farfield, and (b) a close-up of the trawl-door surface.
3.3 Flow Solver
Numerical fluid flow simulations are performed
using the commercial computer code FLUENT
(FLUENT, 2012). The flow solver is coupled
velocity-pressure-based formulation. A velocity inlet
boundary condition is prescribed to all the edges of
the farfield, aside from the outlet edge which has a
pressure outlet boundary condition.
(a)
(b)
Figure 6: An example 3D computational grid, (a) the
farfield, and (b) a close-up of the trawl-door surface.
The spatial discretization schemes are second
order for all flow variables and the gradient
information is found using the Green-Gauss node
based method. Additionally, due to the difficult flow
condition at high angle of attacks, the pseudo-
transient option and high-order relaxation terms are
used in order to get a stable converged solution. The
residuals, which are the sum of the L
2
norms of all
governing equations in each cell, are monitored and
checked for convergence. The convergence criterion
is such that a solution is considered to be converged
if the residuals have dropped by six orders of
magnitude, or the total number of iterations has
reached 6,000 for the 2D model and 2,000 for the
3D model.
3.4 Grid Convergence
A convergence study is performed in order to obtain
a grid that is sufficiently fine to capture the flow
physics accurately. The methodology of the study is
to run the CFD model at the same flow conditions,
but with computational grids of various densities.
The CFD model should capture the flow
characteristics with more accuracy when the grid is
Trawl-doorShapeOptimizationwith3DCFDModelsandLocalSurrogates
777
finer. The purpose of the grid convergence study is
then to determine the grid density that results in
stable simulation results (i.e., not changing upon
further grid refinement). The grid satisfying this
condition is considered to be converged with respect
to the discretization density.
The study is conducted for both 2D and 3D CFD
models using a two-element trawl-door
configuration with the main element shape of NACA
2410 and a leading-edge slat shape of NACA 3210
(shown in Figs. 5 and 6). The leading-edge of the
slat is at (x/c,y/c) = (-0.20,-0.08). The slat is inclined
by
s
= 35°. The free-stream velocity is set at V
∞
= 2
m/s, the angle of attack at α = 20° and the Reynolds
number is Re = 210
6
.
The results of the 2D convergence study shown
in Fig. 7(a) indicate that the grid is converged at
168,592 elements, which is the eighth data point,
counting from the left - the lower boundary of the x-
axis. This grid will be used for the 2D CFD model.
The simulations were executed using four parallel
program nodes, on two Intel Xeon(R) X5660 2.8
GHz processors connected in parallel. The resulting
simulation time needed for each of the data points
are presented in Fig. 7(b). Inspection of Fig. 7(b)
reveals that the simulation runtime decreases
significantly from the third to the fourth data point,
although the element number is higher. As
mentioned before, the convergence criterion is
configured in such way that either all of the residuals
need to be reduced by six orders of magnitude or
that the number of iterations reach up to 6,000. The
solution was converged where all residuals had been
reduced by six orders after less than 2,500 iterations
at the fourth and fifth data points, and that explains
the decreased runtime.
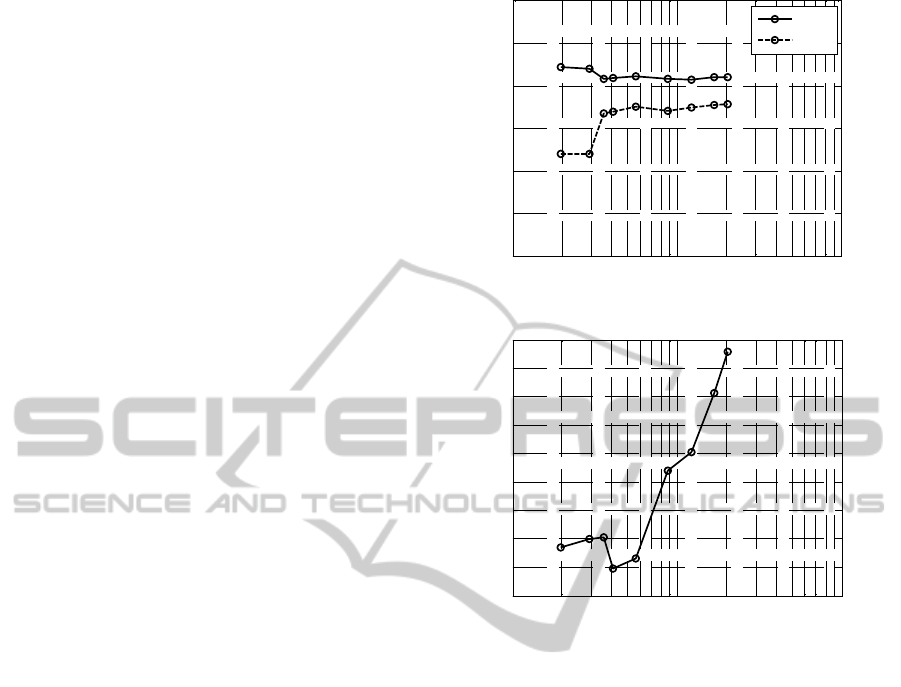
The results of the 3D convergence study shown
in Fig. 8(a) indicate that the grid is converged at
3,972,136 elements, which is the fifth data point,
counting from the left - the lower boundary of the x-
axis. The number of iterations for each of the
simulation runs was 2,000, executed on two Intel
Xeon(R) X5660 processors connected in parallel.
The resulting time needed for each simulation using
the various grids is presented in Fig. 8(b). The
simulation time for the chosen 4 million element
computational grid is therefore around 26 hours. The
simulation time for the sixth data point resulted to be
less than for the fifth one, although the number of
elements is significantly greater. This is caused by
the fact that the solution converged with all residuals
reduced by six orders, before the maximum number
of iterations was reached.
(a)
(b)
Figure 7: Results of a grid convergence study of the 2D
CFD model at V
∞
= 2 m/s and α = 20°; coefficients of (a)
lift and (b) drag versus the number of grid elements.
3.5 Validation
Experimental data is not available for the trawl-door
geometries that are used in this study. Consequently,
other geometries have to be used to validate the CFD
models. For the 2D CFD model, the NACA 0012
airfoil is chosen for the validation process using the
data from Ladson (1988). The 3D CFD model is
compared against the data by Whicker and Fehlner
(1958).
Results for the lift and drag coefficients from the
2D CFD model, compared with the tripped data
from Ladson (1988) are presented in Fig. 9. The
agreement between computational and experimental
data for the lift coefficient versus the angle of attack
is excellent up to the stall region where the
maximum lift occurs (Fig. 9(a)). However, stall
seems to occur at an angle (stall angle of attack) of
16° according to the CFD model, but at an angle of
10
4
10
5
10
6
0
0.5
1
1.5
2
2.5
3
Number of grid elements
C
l
, C
d
x 10
C
l
C
d
x 10
10
4
10
5
10
6
0
20
40
60
80
100
120
140
160
180
Number of grid elements
Time [min.]
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
778

(a)
(b)
Figure 8: Results of a grid convergence study of the 3D
CFD model at V
∞
= 2 m/s and α = 20°; coefficients of (a)
lift and (b) drag versus the number of grid elements.
17° according to the experimental data. A graph of
the lift coefficient versus the drag coefficient is then
presented in Fig. 9(b). Inspection reveals similar
results as the preceding graph, the agreement is good
up to a point when the flow separation increases. In
this case, the agreement is excellent up to a value of
the lift coefficient up to around 1.2.
Results for the lift and drag coefficients from the
3D CFD model, compared with the experimental
data from Whicker and Fehlner (1958) are presented
in Fig. 10. The agreement between the
computational and experimental data for the lift
coefficient versus the angle of attack is excellent up
to a value of around 23° (Fig. 10(a)). According to
the experimental data the stall region occurs at
around 29°. The computational model is not very
reliable when the angle of attack is greater than the
stall angle of attack. Very turbulent flow occurs at
the stall region, and it should be noted that
turbulence modeling is not considered a straight
forward task, especially in 3D modeling (Rumsey et
al., 2010). However, since lift decreases and drag
increases when entered into the stall region, it is not
feasible to operate under such conditions unless a
decrease in velocity is desired. In this study, the aim
is to optimize the aerodynamic characteristics of
trawl-doors, and therefore the desired operating
conditions are at angles less than the stall angle of
attack where the validity of the computational model
is acceptable. It is however evident that the stall
angle of attack is a few degrees smaller according to
the computational results, compared to the
experimental data. Figure 10(b) shows a comparison
between the computational and experimental data of
the drag coefficient versus the lift coefficient. This
graph indicates a similar behaviour as the preceding
ones, stall occurs little earlier in the curve for the
computational results, compared with curve for the
experimental data. The maximum lift coefficient is
therefore lower according to the computational
results is around 1.0, whereas it is around 1.3
according to the experimental data.
(a)
(b)
Figure 9: 2D CFD model validation using NACA 0012.
Experimental data from Ladson (1988) is shown with
triangles and squares.
10
6
10
7
0
0.5
1
1.5
2
2.5
Number of grid elements
C
L
, C
D
x 5
C
L
C
D
x 5
10
6
10
7
0
5
10
15
20
25
30
Number of grid elements
Time [hours]
-5 0 5 10 15 20
-1
-0.5
0
0.5
1
1.5
2
Angle of attack,
[°]
C
l
2D CFD model
Ladson data - grit no. 80
Ladson data - grit no. 120
Ladson data - grit no. 180
-1.5 -1 -0.5 0 0.5 1 1.5 2
0
0.1
0.2
0.3
0.4
0.5
C
l
C
d
2D CFD model
Ladson data - grit no. 80
Ladson data - grit no. 120
Ladson data - grit no. 180
Trawl-doorShapeOptimizationwith3DCFDModelsandLocalSurrogates
779

(a)
(b)
Figure 10: 3D CFD model validation using NACA 0015.
Experimental data from Whicker and Fehlner (1958) is
shown with the triangles.
4 DESIGN METHODOLOGY
4.1 Formulation
The design problem considered in this work can be
formulated as a nonlinear minimization problem of
the form
*
argmin ( )
f
Uf
x
xx
(4)
where f(x) is the function representing performance
parameters of the trawl-door under design (specifically,
the lift and the drag coefficients), whereas x is the
vector of adjustable geometry parameters; U is a given
objective function.
4.2 Optimization by Local Surrogates
The methodology used for trawl-door optimization
exploits local response surface approximation (RSA)
models. The procedure is iterative. In each iteration, a
local model is constructed using sparse samples of f
data and low-order polynomial approximation.
Let x
(j)
= [x
1
(j)
x
2
(j)
… x
n
(j)
]
T
be a design obtained
as a result of iteration j–1 of the algorithm. Let d
(j)
=
[d
1
(j)
d
2
(j)
… d
n
(j)
]
T
be the size parameter that is used
to define the vicinity of the vector x
(j)
. The local
RSA model is created in the interval [x
(j.i)
–
d
(j)
, x
(j.i)
+ d
(j)
]. We denote by X
T
(j)
= {x
t
(j.1)
, …, x
t
(j.N)
}
the training set obtained by sampling the
aforementioned vicinity. The response surface
approximation (RSA) model is obtained by
approximating the data pairs {x
t
(j.k)
,f(x
t
(j.k)
)}, k = 1,
…, N. In this work, a second-order polynomial
model q
(j)
is utilized as follows
∑
∑
(5)
The unknown coefficients
= [
0
1
…
n
11
12
…
1n
22
…
nn
] are found by solving the following
the linear regression problems q(x
t
(j.k)
) = f(x
t
(j.k)
)}, k = 1,
…, N. The unique solution to this problem exists and
can be found analytically assuming that the number of
training points is equal or larger than the number of
unknown coefficients.
It should be noted that although the used RSA
model is very simple, it is sufficient to represent the
CFD-simulated model locally. Also, replacing the
simulation model by the RSA for the purpose of
finding a new candidate design (or, approximated
optimum) allows us to alleviate the problem of
numerical noise always present in CFD simulations.
4.3 Algorithm Workflow
The optimization algorithm workflow is the following
(here, x
(0)
is the initial design, and d
(0)
is the initial
vicinity size, usually, a fraction of the design space
size):
1. Set j = 0;
2. Sample the interval [x
(j.i)
– d
(j)
, x
(j.i)
+ d
(j)
] to
obtain the training set X
T
(j)
;
3. Evaluate the function f at X
T
(j)
;
4. Identify the RSA model q
(j)
;
5. Find a candidate design, x
tmp
, as
() () () ()
()
arg min ( ( ))
jj jj
tmp j
Uq
xd xxd
xx
6. Calculate the gain ratio
()
() () ()
( ( )) ( ( ))
( ( )) ( ( ))
tmp j
jtmp j j
Uf Uf
r
Uq Uq
xx
xx
7. If r > r
incr
, set d
(j+1)
= d
(j)
m
incr
;
8. If r < r
decr
, set d
(j+1)
= d
(j)
/m
decr
;
9. If r > 0, set x
(j+1)
= x
tmp
; otherwise x
(j+1)
= x
(j)
;
10. If the termination condition is satisfied END;
else set j = j + 1 and go to 2;
-5 0 5 10 15 20 25 30
-1
-0.5
0
0.5
1
1.5
2
Angle of attack,
[°]
C
L
3D CFD model
Whicker data
-0.5 0 0.5 1 1.5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
C
L
C
D
3D CFD model
Whicker data
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
780

In the above procedure, the updating parameters
for the trust region size, i.e., r
incr
, m
incr
, r
decr
, and m
decr
are set by the user. In this work, we set r
incr
= 0.75, m
incr
= 1.5, r
decr
= 0.25, and m
decr
= 2. The algorithm is
terminated either if || x
(j+1)
– x
(j)
|| or ||d
(j)
|| are smaller
than a user prescribed threshold. Figure 11 illustrates
the operation of the optimization procedure for n = 2.
Our optimization algorithm is essentially a trust-
region-based procedure with the RSA model used as a
prediction tool. The gain ratio r is used to determine the
quality of prediction made by the model and,
consequently, to update the search radius for the next
iteration. In particular, poor prediction power results in
reducing the search range (and, at the same time, the
validity region for the RSA model). For smaller search
range d, the RSA model becomes better representation
of the CFD-simulated objective. In particular, for
sufficiently small d, the gain ratio will become positive,
i.e., U(f(x
tmp
)) < U(f(x
(j)
)). It should be noted that the
expensive CFD is used both to set up the RSA model
and to verify the new design. We use a very simple
relocation strategy by moving the center of the search
region to the new design (upon its acceptance). Upon
convergence, the search range is decreased, which, at
the same time, leads to improving the accuracy of the
RSA model.
5 RESULTS
Design optimization of modern and airfoil-shaped
trawl-doors is considered using a 3D CFD model
and local surrogates. The design approach is as
follows: (1) shape is optimized in 2D, and (2) the
optimized design from (1) is used as an initial design
for the 3D problem.
5.1 2D Modern Trawl-Door
The objective is to minimize the section drag
coefficient (C
d
) subject to a constraint on the section
lift coefficient (C
l
1.2) as described in Section 2.
The 2D F11 shape is shown in Fig. 2(a). The design
variable vector is x = [x/c y/c
]
T
and the search
domain is set as: 0.4 x/c 0.2, 0.3 y/c 0.3,
20°
50°, 0°
60°. The initial design is x/c
= 0.12, y/c = 0.0085,
= 30°, and
= 0.19°.
The flow speed is V
= 2 m/s and the Reynolds
number is Re = 210
6
. At this condition, we have C
l
= 1.19 and C
d
= 0.08.
Figure 11: A conceptual illustration of the proposed
optimization procedure (n = 2).
To solve the optimization problem we use the
optimization algorithm described in Section 4. A
simple factorial design of experiments (star-
distribution) with 2n + 1 points is used for data
sampling. A second order polynomial is used to fit
the data, and a gradient-based method (the Matlab
(2014) routine fmincon) is employed to search for
the minima.
The numerical results of the design optimization
are presented in Table 1, and the initial and optimum
designs are illustrated in Fig. 12. The optimization
history with an illustration of the optimization path
as well as the vicinity size for each iteration, is
presented in Figs. 13 and 14.
The numerical results show that the lift
coefficient is held constant while the drag coefficient
is reduced by 24%. The resulting increase in the lift-
to-drag efficiency is 32% compared with the initial
design. The lift coefficient at the optimum design is
1.19, violating the lift constraint by less than 1%.
The slat inclination angle hits the lower bound of
20°.
Table 1: Numerical results of the design optimization for
the 2D F11 trawl-door.
Variables Initial Optimized
x/c
0.1200 0.0544
y/c
0.0085 0.0932
[°]
30.00 20.00
[°] 0.19
2.69
C
l
1.19 1.19 0%
C
d
0.08 0.06
24%
C
l
/C
d
14.45 19.08 +32%
Trawl-doorShapeOptimizationwith3DCFDModelsandLocalSurrogates
781

Figure 12: Initial and optimized shapes of the 2D F11
trawl-door. The flow direction is parallel to the x-axis.
Figure 13: Optimization history of the 2D F11 trawl-door
showing the lateral (x/c) and vertical (y/c) position of the
slats leading-edge.
Figure 14: Optimization history of the 2D F11 trawl-door
showing the inclination of the slats (
) and the flow angle
of attack (
).
5.2 3D Modern Trawl-Door
The 3D optimization is formulated in the same way
as the 2D one described in Section 5.2. However, the
minimum lift coefficient is now set as C
L
*
= 1.0. The
initial section shape is set as the optimum design
obtained in the 2D case. The span of the trawl-door
is set as 6.0 m and the aspect ratio is 2.4.
Table 2: Numerical results of the design optimization for
the 3D F11 trawl-door.
Variables Initial Optimized
x/c
0.0544 0.0600
y/c
0.0932 0.0732
[°]
20.00 20.00
[°]
2.69 0.69
C
l
1.00 1.00 0%
C
d
0.14 0.13
6%
C
l
/C
d
7.52 7.55 +6%
Figure 15: Initial and optimized shapes of the 3D F11
trawl-door. The flow direction is parallel to the x-axis.
The numerical results of the 3D design
optimization are presented in Table 2. The 3D
optimum design, compared with the initial and
optimum 2D designs are presented in Fig. 15. The
results show that the values for the lift coefficient is
held constant while the drag coefficient is reduced
by 6% with the corresponding increase by 6% in the
lift-to-drag ratio. All the design variables are
adjusted slightly, aside from the slat inclination
angle, which is still at the lower bound.
5.3 2D Airfoil-Shaped Trawl-Door
The 2D airfoil-shaped trawl-door configuration is
shown in Fig. 2(b). The element shapes are kept
fixed. The main element has the shape of NACA
2412 and the leading-edge slat has the shape of
NACA 3210. The initial design configuration is: x/c
= 0.20, y/c = 0.08,
= 25°, and
= 8.59°. The
optimization problem is formulated the same way as
described in Section 5.1.
The numerical results of the design optimization
are presented in Table 3, and the initial and optimum
designs are illustrated in Fig. 16. The optimization
history with an illustration of the optimization path
as well as the vicinity size for each iteration, is
presented in Figs. 17 and 18.
The drag coefficient is reduced by 12% while
holding the lift coefficient constant. Again, the slat
inclination angle is near the lower bound.
-0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2
-0.1
0
0.1
0.2
0.3
x/c
y/c
Initial
Optimized
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
(x/c)
slats
(y/c)
slats
Design Space
Iteration 1
Iteration 2
Iteration 3
Iteration 4
Iteration 5
Iteration 6
Iteration 7
Iteration 8
Iteration 9
Optimization Path
Initial Design
Optimized Design
0 10 20 30 40 50 60
15
20
25
30
35
40
45
50
55
[°]
[°]
Design Space
Iteration 1
Iteration 2
Iteration 3
Iteration 4
Iteration 5
Iteration 6
Iteration 7
Iteration 8
Iteration 9
Optimization Path
Initial Design
Optimized Design
-0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2
-0.1
0
0.1
0.2
0.3
x/c
y/c
2D initial
3D initial (2D opt.)
3D optimized
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
782

Table 3: Numerical results of the design optimization for
the 2D airfoil-shaped trawl-door.
Variables Initial Optimized
x/c
0.2000 0.2288
y/c
0.0800 0.0066
[°]
25.00 20.50
[°]
8.59 8.28
C
l
1.20 1.20 0%
C
d
0.020 0.017
12%
C
l
/C
d
60.84 69.88 +12%
Figure 16: Initial and optimized shapes of the 2D airfoil-
shaped trawl-door. The flow direction is parallel to the x-
axis.
Figure 17: Optimization history of the 2D airfoil-shaped
trawl-door showing the lateral (x/c) and vertical (y/c)
position of the slats leading-edge.
Figure 18: Optimization history of the 2D airfoil-sahped
trawl-door showing the inclination of the slats (
) and the
flow angle of attack (
).
5.4 3D Airfoil-Shaped Trawl-Door
The 3D optimization task for the airfoil-shaped
trawl-door is formulated in the same way as the 3D
optimization of the F11 shape (described in Section
5.2). Table 4 shows the numerical results and Fig. 19
shows the initial and optimized designs.
The drag coefficient is reduced by 5% with the
corresponding increase by 6% in the lift-to-drag
ratio. There is a significant change is the shape from
2D to 3D indicating the importance of 3D flow
effects.
6 CONCLUSION
In this paper, a sequential approximate optimization
technique for hydrodynamic design of trawl-door
shapes has been presented. The design is based on
high-fidelity CFD simulation models. For the sake
of design cost reduction as well as reliability of the
optimization process, we utilize low-order
polynomial models and trust-region framework as a
convergence safeguard. Numerical studies are
carried out for both 2D and 3D cases with the final
designs obtained in a few iterations of the
optimization algorithm.
Table 4: Numerical results of the design optimization for
the 3D airfoil-shaped trawl-door.
Variables Initial Optimized
x/c
0.2288 0.0600
y/c
0.0066 0.0266
[°]
20.50 20.00
[°]
7.38 7.21
C
l
1.00 1.00 0%
C
d
0.050 0.047
5%
C
l
/C
d
14.56 15.76 +6%
Figure 19: Initial and optimized shapes of the 3D airfoil-
shaped trawl-door. The flow direction is parallel to the x-
axis.
-0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2
-0.2
0
0.2
x/c
y/c
Initial
Optimized
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
(x/c)
slat
(y/c)
slat
Design Space
Iteration 1
Iteration 2
Iteration 3
Iteration 4
Iteration 5
Iteration 6
Iteration 7
Iteration 8
Iteration 9
Optimization Path
Initial Design
Optimized Design
0 10 20 30 40 50 60
15
20
25
30
35
40
45
50
55
[°]
[°]
Design Space
Iteration 1
Iteration 2
Iteration 3
Iteration 4
Iteration 5
Iteration 6
Iteration 7
Iteration 8
Iteration 9
Optimization Path
Initial Design
Optimized Design
-0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2
-0.2
0
0.2
x/c
y/c
2D initial
3D initial (2D opt.) 3D optimized
Trawl-doorShapeOptimizationwith3DCFDModelsandLocalSurrogates
783

REFERENCES
FLUENT, ver. 14, ANSYS Inc., Southpointe, 275
Technology Drive, Canonsburg, PA 15317, 2012.
Garner, J., Botnvarpan og bunadur hennar, Fiskifelag
Islands, 1967.
Haraldsson, H.O., “Fluid Dynamics Simulation of Fishing
Gear,” M.Sc. Thesis, University of Iceland, May 1996,
ICEM CFD, ver. 14, ANSYS Inc., Southpointe, 275
Technology Drive, Canonsburg, PA 15317, 2012.
Jonsson, E., Leifsson, L., and Koziel, S. “Trawl-Door
Performance Analysis and Design Optimization with
CFD”, 2nd Int. Conf. on Simulation and Modeling
Methodologies, Technologies, and Applications
(SIMULTECH), Rome, Italy, July 28-31, 2012.
Jonsson, E., Hermannsson, E., Juliusson, M., Koziel, S.,
and Leifsson, L. “Computational Fluid Dynamic
Analysis and Shape Optimization of Trawl-Doors,”
51st AIAA Aerospace Sciences Meeting including the
New Horizons Forum and Aerospace Exposition,
Grapevine, Texas, January 7-10, 2013.
Ladson, C.L., “Effects of Independent Variation of Mach
and Reynolds Numbers on the Low-Speed
Aerodunamic Characteristics of the NACA 0012
airfoil Section,” NASA Technical Memorandum 4074,
NASA, 1988.
Leifsson, L., Koziel, S., Hermannsson, E., and Reza
Fakhraie, “Trawl-Door Design Optimization by Local
Surrogate Models,” 55th AIAA/ASMe/ASCE/AHS/SC
Structures, Structural Dynamics, and Materials
Conference, National Harbor, MD, January 2014.
Matlab, ver. R2014a, The Mathworks Inc., Natick,
Massachusetts, U.S.A, 2014.
Rumsey, C. L., Smith, B. R., and Huang, G. P.,
“Description of a Website Resource for Turbulence
Modeling Verification and Validation,” 40th AIAA
Fluid Dynamics Conference and Exhibit, AIAA Paper
2010-4742, Chicago, U.S.A., July 2010.
Tannehill, J.A., Anderson, D.A., and Pletcher, R.H.,
Computational fluid mechanics and heat transfer, 2nd
edition, Taylor & Francis, 1997.
Whicker, L. F., and Fehlner, L. F. “Free-Stream
Characteristics of a Family of Low-Aspect Ratio, All-
Movable Control Surfaces for Application to Ship
Design,” National Technical Information Service, U.S.
Department of Commerce, U.S.A, December 1958.
SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
784
