Simplified Information Acquisition Method to Improve
Prediction Performance: Direct Use of Hidden Neuron
Outputs and Separation of Information Acquisition
and Use Phase
Ryotaro Kamimura
IT Education Center and School of Science and Technology, Tokai Univerisity,
1117 Kitakaname, Hiratsuka, Kanagawa 259-1292, Japan
Abstract. In this paper, we propose a new type of information-theoretic method
to improve prediction performance in supervised learning with two main techni-
cal features. First, the complicated procedures to increase information content is
replaced by the direct use of hidden neuron outputs. We realize higher informa-
tion by directly changing the outputs from hidden neurons. In addition, we have
had difficulty in increasing information content and at the same time decreasing
errors between targets and outputs. To cope with this problem, we separate infor-
mation acquisition and use phase learning. In the information acquisition phase,
the auto-encoder tries to acquire information content on input patterns as much
as possible. In the information use phase, information obtained in the phase of
information acquisition is used to train supervised learning. The method is a sim-
plified version of actual information maximization and directlydeals with the out-
puts from neurons. We applied the method to the protein classification problem.
Experimental results showed that our simplified information acquisition method
was effective in increasing the real information content. In addition, by using the
information content, prediction performance was greatly improved.
1 Introduction
Neural network try to store information content on input patterns as much as possible.
Thus, it is necessary to examine how and to what extent information should be stored
within neural networks. Linsker stated explicitly this information acquisition in neural
networks as the well-known information maximization principle [1], [2], [3], [4]. This
means that neural networks try to maximize information content in every information
processing stage.
Following Linsker’s information principle, we developedinformation theoretic meth-
ods to control the quantity of information on input patterns [5], [6], [7]. We have so
far succeeded in increasing information content, keeping training errors between tar-
gets and outputs relatively small. However, we have had several problems of those
information-theoretic methods to be solved in the course of experiments.
Among them, the most serious ones are the inability to increase information, com-
putational complexity and compromise between information maximization and error
Kamimura R..
Simplified Information Acquisition Method to Improve Prediction Performance: Direct Use of Hidden Neuron Outputs and Separation of Information
Acquisition and Use Phase.
DOI: 10.5220/0005134700780087
In Proceedings of the International Workshop on Artificial Neural Networks and Intelligent Information Processing (ANNIIP-2014), pages 78-87
ISBN: 978-989-758-041-3
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

minimization,First, we have observedsome cases where the information-theoreticmeth-
ods do not necessarily succeed in increasing information content. For example, when
the number of neurons increases, the adjustment among neurons becomes difficult,
which prevents neural networks from increasing information content. Then, we have
a problem of computational complexity. As experted, information or entropy functions
gives complex learning formula. This also suggests that the information-theoreticmeth-
ods can be effective only for the relatively small sized neural networks. Third, we have
a problem of compromise between information maximization and error minimization.
From the information-theoretic points of view, information on input patterns should
be increased. However, neural networks should minimize errors between targets and
outputs. We have observed that information maximization and error minimization are
sometimes contradictory to each other. This mean that it is difficult to comprise between
information maximization and error minimization in one framework.
We here propose a new information-theoretic methods to facilitate information ac-
quisition in neural networks. Instead of directly dealing with the entropy function, we
realize a process of information maximization by using the outputs from neurons with-
out normalizing the outputs for the probability approximation. This direct use of outputs
can facilitate a process of information maximization and eliminate the computational
complexity.
In addition, we separate information acquisition and use phase. We first try to ac-
quire information content in input patterns. Then, we use obtained information content
to train supervised neural networks. This eliminates contradiction between information
maximization and error minimization. The effectiveness of separation has been proved
to be useful in the field of deep learning [8], [9], [10], [11]. Different from those meth-
ods, our method tries to create actively necessary information for supervised learning.
2 Theory and Computational Methods
2.1 Simplified Information Maximization
We developedthe information-theoreticmethods to increase information content in hid-
den neurons on input patterns. We have so far succeeded in increasing the information
content to a large quantity [5], [6], [7]. However, the method was limited to networks
with a relatively smaller number of hidden neurons because of the computational com-
plexity of the information method. In addition, we found that the obtained information
content did not necessarily contribute to improved prediction performance.
The computational complexity of the information-theoretic methods can be atten-
uated by dealing directly with the outputs from the neurons. We try to approximate
higher information by producing the hidden patterns achieved by the real information
maximization.
Information in Hidden Neurons. We here explain how to compute the information
and approximate it for simplification. Let x
s
k
and w
jk
denote the kth element of the
sth input pattern and connection weights from the kth input neuron to the jth hidden
79

neuron in Figure 1, then the net input is computed by
u
s
j
=
L
X
k=1
w
jk
x
s
k
, (1)
where L is the number of input neurons. The output is computed by
v
s
j
= f(u
s
j
), (2)
where we here use the sigmoid activation function. The averaged output is defined by
v
j
=
1
S
S
X
s=1
v
s
j
, (3)
where S is the number of input patterns. The firing probability of the jth hidden neuron
is obtained by
p(j) =
v
j
P
M
m=1
v
s
m
(4)
The entropy is defined by
H = −
M
X
j=1
p(j) log p(j), (5)
where M is the number of hidden neurons. The information is defined as decrease of
entropy from its maximum value
I = H
max
− H (6)
Simplified Information Maximization. We can directly differentiate the information
or entropy function in the equation (5). However, in actual situations, we have had
difficulty in increasing the information or to decrease the entropy. In particular, when
the number of hidden neurons was large, we had difficulty in increasing the information
content.
Thus, we try to realize this information increase by using the actual outputs from
hidden neurons. When the information becomes larger or the entropy becomes smaller,
a small number of hidden neurons tend to fire, while all the others become inactive.
To realize this situation, we consider the winners in hidden neurons. Let c
j
denote the
index of the jth winner, then the rank order of the winners are
c
1
< c
2
< c
3
< ... < c
M
. (7)
We here suppose that the winning neurons keep the following relations
v
c
1
> v
c
2
> v
c
3
... > v
c
M
(8)
Thus, when the outputs from neurons become larger, the degree of winning becomes
higher. For higher information, a small number of hidden neurons only fires, while all
80

the others cease to fire. Thus, we suppose that the winning neurons should have the
following outputs
ρ
j
=
β
c
j
, 0 < β < 1 (9)
where β is a parameter to control the degree of winning and ranges between zero and
one. To decrease the entropy, we must decrease the following KL-divergence
KL =
M
X
j=1

ρ
j
log
ρ
j
v
j
+ (1 − ρ
j
) log
1 − ρ
j
1 − v
j
.

(10)
When the KL divergence becomes smaller, a smaller number of winning neurons tend
to fire, while all the other neurons become inactive.
2.2 Separation of Information Acquisition and Use Phase
We have found that the information maximization is contradictory to the error mini-
mization. In maximizing the information, the errors between targets and outputs cannot
be decreased. Recently, the use of unsupervised learning turned out to be effective in
training multi-layered networks [8], [9], [10], [11]. Thus, we separate the information
acquisition procedure from the information use. Figure 1 shows this situation of sep-
aration. In the information acquisition phase in Figure 1(a), the auto-encoder is used
and the information content in hidden neurons is increased as much as possible. Then,
using connection weights obtained by the information acquisition phase, learning is
performed in supervised ways in Figure 1(b).
Information Acquisition Phase. We here explain computational procedures for the
information acquisition phase. The output from the output neuron in the auto-encoder
in Figure 1(a) is computed by
o
s
k
= f


M
X
j=1
W
kj
v
s
j


, (11)
where W
kj
denote connection weights to output neurons. Thus, the error is computed
by
E =
1
2S
S
X
s=1
L
X
k=1
(x
s
k
− o
s
k
)
2
(12)
To increase information, we should decrease the entropy. In the information acquisition
phase, we use the auto-encoder. Thus, we must decrease
J =
1
2S
S
X
s=1
L
X
k=1
(x
s
k
− o
s
k
)
2
− γ
M
X
j=1
p(j) log p(j), (13)
where γ is a parameter to control the effect of the entropy term.
81

x
k
s
s
x
k
s
o
k
s
v
j
w
jk
W
kj
(a) Information acuisition phase
Input
Hidden
Output
Target
x
k
s
s
y
i
s
o
i
w
jk
*
W
ij
(b) Information use phase
Input
Hidden
Output
Fig.1. Network architecture for supervised learning with an information acquisition (a) and use
phase (b).
Simplified Information Acquisition Phase. The equation to be minimized is
J =
1
2S
S
X
s=1
L
X
k=1
(x
s
k
− o
s
k
)
2
+γ
M
X
j=1

ρ
j
log
ρ
j
v
j
+ (1 − ρ
j
) log
1 − ρ
j
1 − v
j

, (14)
where γ is a parameter to control the effect of the KL-divergence. By differentiating the
equation, we have
∂J
∂w
jk
=
1
S
S
X
s=1
δ
s
j
x
s
k
, (15)
82

where
δ
s
j
=
"
L
X
k=1
W
kj
δ
s
k
+ γ

−
ρ
j
v
j
+
1 − ρ
j
1 − v
j

#
f
′
(u
j
), (16)
where δ
s
k
denote the error signals from the output layer.
Information Use Phase. In the information use phase, connection wights obtained
by the information acquisition phase are used as initial ones. Let w
∗
jk
denote initial
connection weights provided by the information acquisition phase, then the output from
the hidden neuron is computed by
v
s
j
= f
L
X
k=1
w
∗
jk
x
s
k
!
. (17)
In the output layer, we use the sofmax output computed by
o
s
i
=
exp(
P
M
j=1
W
ji
v
s
j
)
P
N
m=1
exp(
P
M
j=1
W
jm
v
s
j
)
, (18)
where W
ji
are connection weights from the hidden neurons to the output ones. The
error is computed by
E = −
S
X
s=1
N
X
i=1
y
s
i
log o
s
i
, (19)
where y is the target and N is the number of output neurons. We can differentiate this
error function with respect to connection weights in the competitive and output layer.
We here show the update formula for the first competitive layer
∂J
∂w
jk
=
1
S
S
X
s=1
δ
s
j
x
s
k
, (20)
where
δ
s
j
=
N
X
i=1
W
ij
δ
s
i
, (21)
where δ is the error signal sent from the output layers and η is a learning parameter.
3 Results and Discussion
3.1 Experimental Results
Experimental Outline. In the experiment, we try to show that our simplified method
83

8 output neurons
8 input neurons
10 output neurons
(a) Information acquisition phase
(b) Information use phase
50 hidden neurons
Fig.2. Network architecture for the protein classification problem with the information acquisi-
tion phase (a) and use phase (b).
can be used to increase the information content by firing a smaller number of hidden
neurons. In addition, prediction performance can greatly be improved by controlling the
information content.
To demonstrate the performance of our method, we used the protein classification
problem [12]. The number of patterns was 1484, and the numbers of training and vali-
dation patterns were 500. The remaining patterns were for testing. The numbers of input
and output neurons were eight in the information acquisition phase in Figure 2 (a). In
the information use phase in Figure 2(b), the number of output neurons became ten,
representing ten classes. First, the auto-encoder was used to store information on input
patterns as shown in Figure 2(a). Then, weights to hidden neurons were used as initial
weights for the supervised learning in Figure 2(b).
Information Acquisition. First, we examined whether our simplified methods were
effective in increasing information content
I = log M +
M
X
j=1
p(j) log p(j). (22)
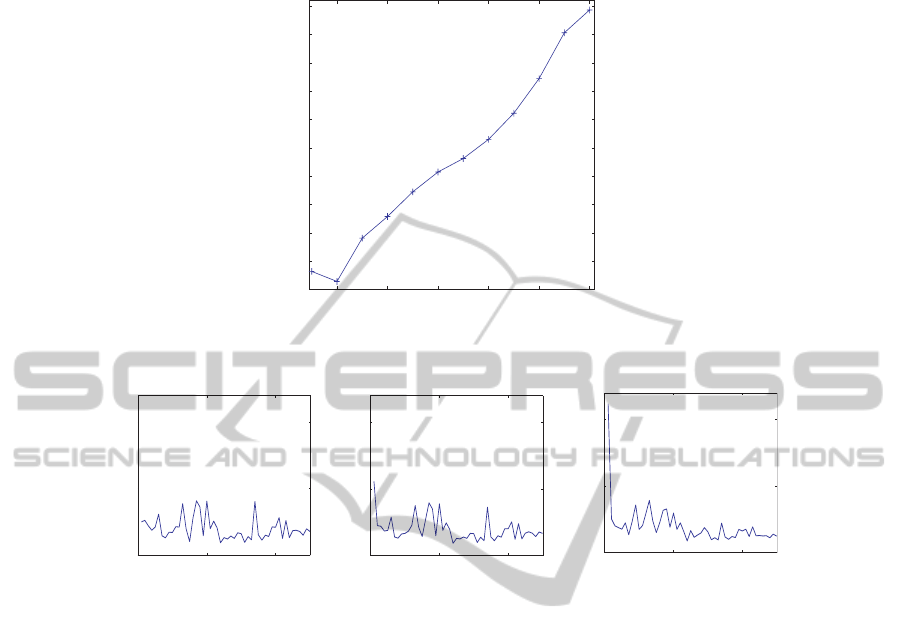
Figure 3 shows information as a function of the parameter β. Information should in-
crease when the parameter β increases. A smaller number neurons tend to fire, when
the information increases as can be expected by the equation
KL =
M
X
j=1

ρ
j
log
ρ
j
v
j
+ (1 − ρ
j
) log
1 − ρ
j
1 − v
j

. (23)
On the other hand, when the parameter β decreases, the firing rates of all hidden neurons
become smaller.
84

0.08
0.09
0.
1
0.11
0.12
0.13
0.14
0.15
0.16
0.17
Information
0.01
0.46
Beta
0.99
Fig.3. Information as a function of the parameter β for the protein classification data.
0 20 40
0
0.05
0.
1
0 20 40
0
0.05
0. 1
0 20 40
0
0.05
0. 1
Hidden neurons
Hidden neurons Hidden neurons
Firing rates
Firing rates
Firing rates
(a) 0.01
(c) 0.99
(b) 0.19
Fig.4. Firing probabilities p(j) when the parameter β increased from 0.01 (a) to 0.99 (l).
As can be seen in the figure, when the parameter β increased, the information in-
creased constantly except when the parameter β was changed from 0.0 to 0.1. This
means that the simplified method was effective in increasing information content. Fig-
ure 4 shows the firing probabilities p (j) of fifty hidden neurons. When the parameter
β was 0.01 in Figure 4(a), all neurons fires with low firing probabilities. When the pa-
rameter β increased to 0.19 in Figure 4(b), the first hidden neuron tended to fire the
most strongly. Then, when the parameter increased to 0.99 in Figure 4(c), the first hid-
den neuron became dominant in terms of the firing probability. The results showed that
when the parameter β increased, one hidden neuron only strongly fired.
Classification Errors. Then, we examined how the obtained information affected the
classification rates for testing data. Figure 5 shows the classification errors as a function
of the parameter β. Without information provided by the auto-encoder, the error rate
was 0.395. This means that all error rates by our method were lower than this error rate
obtained without the information content. In particular, when the parameter β was 0.37,
we have the lowest error of 0.353. The experimental results showed that by controlling
the information content, improved prediction performance could be obtained.
85

0.35
0.355
0.36
0.365
0.37
0.375
0.38
0.385
0.39
0.395
Error rate
0.01
0.37
Beta
0.99
Without information=0.395
0.353
Fig.5. Classification errors when the parameter β increased from 0.01 to 0.99.
4 Conclusion
In this paper, we have proposed a new type of information-theoretic method to improve
prediction performance. In the method, the complex procedures of information max-
imization are replaced by the approximation method. The method directly deals with
outputs from hidden neurons. In addition, the information acquisition and use phase
are separated. In the information acquisition phase, information content in hidden neu-
rons is increased by producing a small number of active hidden outputs. On the other
hand, in the information use phase, the information obtained in the information acqui-
sition phase, is used to train supervised learning. We applied the method to the pro-
tein classification problem. Experimental results showed that the information increased
by our method and the improved prediction performance was obtained. Though the
information-theoretic methods have given tools to examine how neural networks ac-
quires information content on input patterns, their learning rules were complicated for
the actual applications. Our proposed method is simple enough to be applied to many
problems, in particular, to large sized data.
References
1. R. Linsker, “Self-organization in a perceptual network,” Computer, vol. 21, pp. 105–117,
1988.
2. R. Linsker, “How to generate ordered maps by maximizing the mutual information between
input and output,” Neural Computation, vol. 1, pp. 402–411, 1989.
3. R. Linsker, “Local synaptic rules suffice to maximize mutual information in a linear net-
work,” Neural Computation, vol. 4, pp. 691–702, 1992.
4. R. Linsker, “Improved local learning rule for information maximization and related applica-
tions,” Neural Networks, vol. 18, pp. 261–265, 2005.
5. R. Kamimura and S. Nakanishi, “Improving generalization performance by information min-
imization,” IEICE Transactions on Information and Systems, vol. E78-D, no. 2, pp. 163–173,
1995.
6. R. Kamimura and S. Nakanishi, “Hidden information maximization for feature detection and
rule discovery,” Network, vol. 6, pp. 577–622, 1995.
86

7. R. Kamimura and T. Kamimura, “Structural information and linguistic rule extraction,” in
Proceedings of ICONIP, pp. 720–726, 2000.
8. G. E. Hinton, “Learning multiple layers of representation,” Trends in cognitive sciences,
vol. 11, no. 10, pp. 428–434, 2007.
9. Y. Bengio, “Learning deep architectures for ai,” Foundations and trends
R
 in Machine Learn-
ing, vol. 2, no. 1, pp. 1–127, 2009.
10. G. E. Hinton and R. R. Salakhutdinov, “Reducing the dimensionality of data with neural
networks,” Science, vol. 313, no. 5786, pp. 504–507, 2006.
11. G. E. Hinton, S. Osindero, and Y.-W. Teh, “A fast learning algorithm for deep belief nets,”
Neural computation, vol. 18, no. 7, pp. 1527–1554, 2006.
12. K. Bache and M. Lichman, “UCI machine learning repository,” 2013.
13. I. Guyon and A. Elisseeff, “An introduction to variable and feature selection,” Journal of
Machine Learning Research, vol. 3, pp. 1157–1182, 2003.
14. A. Rakotomamonjy, “Variable selection using SVM-based criteria,” Journal of Machine
Learning Research, vol. 3, pp. 1357–1370, 2003.
15. S. Perkins, K. Lacker, and J. Theiler, “Grafting: Fast, incremental feature selection by gradi-
ent descent in function space,” Journal of Machine Learning Research, vol. 3, pp. 1333–1356,
2003.
87