
ANFIS Traffic Signal Controller for an Isolated Intersection
Sahar Araghi, Abbas Khosravi and Douglas Creighton
Center for Intelligent Systems Research (CISR), Deakin University, Victoria 3216, Australia
Keywords:
Traffic Signal Controlling, Fuzzy Logic Systems, ANFIS, Isolated Intersection.
Abstract:
Traffic signal controlling is one of the solutions to reduce the traffic congestion in cities. To set appropriate
green times for traffic signal lights, we have applied Adaptive Neuro-Fuzzy Inference System (ANFIS) method
in traffic signal controllers. ANFIS traffic signal controller is used for controlling traffic congestion of a single
intersection with the purpose of minimizing travel delay time. The ANFIS traffic controller is an intelligent
controller that learns to set an appropriate green time for each phase of traffic signal lights at the start of the
phase and based on the traffic information. The controller uses genetic algorithm to tune ANFIS parameters
during learning time. The results of the experiments show higher performance of the ANFIS traffic signal
controller compared to three other traffic controllers that are developed as benchmarks. One of the benchmarks
is GA-FLC (Araghi et al., 2014), next one is a fixed-FLC, and a fixed-time controller with three different values
for green phase. Results show the higher performance of ANFIS controller.
1 INTRODUCTION
Increasing traffic density is one of the unpleasant out-
comes of the urbanization. Traffic congestion has
many harmful side effects. Creating environmen-
tal and health hazards, generating a huge amount of
green house gas, increasing the amount of fuel con-
sumption, wasting time in traffic queues are some of
these side effects (Iqbal et al., 2012a).
Through the studies, to control traffic signal tim-
ing, different categories have been defined for traffic
control systems. One of these categories considers
three generations; fixed-time or predefined method
is the first generation that requires pre-set signal se-
quences. Traffic Network Study Tool (Robertson,
1969)(Vincent et al., ) is one of the methods for de-
termining effective pre-set signals. In the second gen-
eration the signal timing adjusts based on the de-
tected traffic situation. Split Cycle Offset Optimiza-
tion Technique (Hunt et al., 1982), and Sydney Co-
ordinated Adaptive Traffic System (Luk, 1984) are
the popular samples of the second generation. Third
generation is for distributed control and based on dy-
namic decision making. Control method in third gen-
eration is fully adaptive and optimization of signal
timing is done progressively (Cai et al., 2009). OPAC
(Gartner, 1982)(Gartner et al., ) and RHODES (Mir-
chandani and Head, 2001) are some examples of this
generation.
Adaptive systems have both offline and online
types. Offline type benefits a database of pre-stored
signal control plans. The pre-stored plans are devel-
oped by historical traffic data. Plan selection is di-
rectly related to the date and time to have the best
suitable plan for current traffic condition. For offline
type there is always this issue that the registered traffic
conditions considered for that time of the week may
become out-dated or changed gradually then not be
suitable anymore. Decision making in online type is
based on real-time traffic situation detected and pre-
dicted values. progressive optimization is possible ev-
ery five to fifteen minutes in online mode.
The conventional traffic controlling methods are
not suitable solution for fluctuating and increasing
traffic condition. Traffic flows in urban area are
vague, complex, random and fuzzy that make it dif-
ficult to propose a pre-defined formula for traffic con-
trolling (Wannige and Sonnadara, 2009). In this
situation Artificial Intelligence (AI) techniques that
are able to think like human are useful for control-
ling traffic congestion at an intersection (Udofia and
Emagbetere, 2013).
Many attempts have been done to apply AI tech-
niques to improve the performance of the controlling
(Spall and Chin, 1997)(Chin et al., 2011)(Schouten,
2007)(Cai et al., 2009). For example, Choy(Chee,
175
Araghi S., Khosravi A. and Creighton D..
ANFIS Traffic Signal Controller for an Isolated Intersection.
DOI: 10.5220/0005135001750180
In Proceedings of the International Conference on Fuzzy Computation Theory and Applications (FCTA-2014), pages 175-180
ISBN: 978-989-758-053-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2005) proposed a hybrid approach in which they ap-
plied computational intelligence concepts to imple-
ment a cooperative, multiagent system for a large-
scale traffic network. The problem of controlling
the network was divided between various agents who
made decision by fuzzy neural control systems. Ap-
plying the proposed system for controlling traffic sig-
nal timing in a part of the Central Business District
of Singapore showed reducing total vehicle stoppage
time by 50% and the total mean delay by 40% com-
pared to real-time adaptive traffic control system.
Fuzzy logic system (FLS) is a powerful tool for
situations where implementation of the exact math-
ematical model is difficult or impossible (Niittymki,
2001). Pappis and Mamdani are pioneers of im-
plementation a fuzzy logic controller for an isolated
intersection with two one-way streets (Pappis and
Mamdani, 1977). Researchers (Favilla et al., 1993)
have also applied FLS to control a single intersection
with two-way streets. In this work the number of ve-
hicles that had already passed the intersection and the
length of the queue of the red approach formed the
Fuzzy Logic controller (FLC) inputs and the amount
of extension of green time was the output of the FLS.
Nair and Cai (Nair and Cai, 2007), proposed a
FLC aimed to ensure smooth flow of traffic and reduc-
ing the delay time. It is usually attempted to optimize
the performance of the network by maximizing traffic
flows or minimizing traffic delays under typical traffic
conditions, consequently, these controllers are not the
optimal for exceptional traffic cases such as road acci-
dents. This research proposes an FLC able to control
traffic flows under both normal and exceptional traffic
conditions by different traffic detector sensors placed
at incoming and outgoing links. Many other studies
also used FLC for a single intersection (Wei et al.,
2001)(Wei et al., 2001)(Hu et al., 2007)(Zeng et al.,
2007).
Different studies are done in controlling traffic
signal lights at intersections, in some studies fixed
predefined green times are used based on traffic con-
gestion (Abdoos et al., 2011)(Abdoos et al., 2013)
which reduces the flexibility of cycle times. In
some other works just extension or termination of the
green phase are computable (Pappis and Mamdani,
1977)(Favilla et al., 1993)(Bazzan, 2009)(El-Tantawy
et al., 2013). The number of extensions can be con-
tinued up to reaching the maximum number. In this
case there is no estimation of the end of the phase.
Researchers who used FLS for designing traffic con-
troller usually apply manually tunning process in gen-
erating fuzzy rules based on expert knowledge. Since
there is no organized approach used by human to cre-
ate these rules, the tunning process can be error-prone
and time consuming.
In this paper, Adaptive Neuro-fuzzy Inference
System (ANFIS) is applied to control traffic conges-
tion by allocating appropriate time to traffic signal
phases. ANFIS method utilized both neural network
(NN) which is very fast process and FLS with the ca-
pability of human reasoning (Iqbal et al., 2012b). In
this situation it is not necessary to predefine the rule
base and ANFIS finds its optimal parameters through
training. The proposed controllers make it possible to
have different ranges of green times with flexible cy-
cle time. Before start of each phase the appropriate
green times for that phase is estimated and sent to the
controller. We evaluate the performance of the ANFIS
controller with one of our previous studies GA-FLC
(Araghi et al., 2014) and a FLC uses predefined pa-
rameters in its fuzzy sets named fixed-FLC. In addi-
tion, a fixed-time controller with three different values
for its green phase time is included in performance
evaluation tests.
The rest of this paper is organized as follows. In
section 2, the designed ANFIS controller is intro-
duced. Section 3, represents experimental results and
discussion and finally conclusion is in section 4.
2 PROPOSED ANFIS TRAFFIC
SIGNAL TIMING
CONTROLLER
ANFIS model has a combination of both NN and
Fuzzy Systems (FS). One of the difficulty in apply-
ing FLC for a system is how to define the appropori-
ate rule base to obtain the best efficiency of the FLC.
In ANFIS system first order Sugeno model fuzzy sys-
tem modifies the rules and adaptively learns to reach
the optimal parameters for the rule base.
Here, an ANFIS controller is designed for a four-
way intersection. This controller has four inputs and
one output. The queue length of vehicles at each ap-
proaching link of the four-way intersection make the
inputs of the controller and the output of the system
is the proposed green time for the current phase of the
cycle. At the end of each phase the detected length of
queues of all the approaching links are sent to the AN-
FIS controller and the controller sends the green time
for the next phase. During the training Genetic Al-
gorithm (GA) evaluates the performance of the con-
troller with different parameters until reach the op-
timal parameters for the ANFIS controller. Average
delay time of a complete run of a simulation is con-
sidered as the cost function for the GA. It means GA
aimed to reduce average delay time of the whole net-
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
176

Queue Lengths
ANFIS
Green Time
Cost Function
Traffic Simulator
(PARAMICS)
Input
Output
GA
(in whole simulation)
Update Parameters
Average Delay
Each Phase
Each Round of Simulation
Figure 1: The figure shows the process of ANFIS training.
ANFIS parameters are updated after each round of simula-
tion through genetic algorithm optimization method.
work in finding optimal parameters Eq. 1.
cost f unction =
∑
n
i=1
d
i
k
(1)
where i = 1, . . . , n is the number of phases executed
during the simulation time, d is the calculated delay
time for each phase, and k is the number of cars re-
leased in each simulation scenario.
The implemented ANFIS controller is for inter-
section with four approaching links. This means the
ANFIS controller has four inputs. ANFIS use Sugeno
type fuzzy systems. Three membership functions
are considered for inputs named small, medium, and
large. The design and training process of ANFIC con-
troller are presented in Fig. 1.
3 EXPERIMENTS
ENVIRONMENT AND RESULTS
DISCUSSION
An intersection with four approaching links and four
phases is designed in Paramics V6.8.0. Fig. 2 shows
the designed platform. The total time divided between
defined four phases is the cycle time. This time is
divided between these four traffic phases. Vehicles
in each lane get permission to cross the intersection
based on the related green time and direction of the
phase. The cycle time is assumed to be unfixed to
have more flexibility in controlling system according
to traffic demand. Zones are the areas that vehicles
are released from them to the intersection and we con-
sider four zones in our simulation. Matlab R2011b is
used to implement the controller.
As it is mentioned in previous section we have
considered three membership functions for each in-
Figure 2: Snapshot of four defined phases at an isolated
intersection in Paramics.
0 10 20 30 40 50 60 70 80 90 100
10
20
30
40
50
60
70
Generation
Fitness value
Best: 16.3109 Mean: 18.9095
Best fitness
Mean fitness
Figure 3: Convergence of genetic algorithm during optimiz-
ing ANFIS parameters.
put of the ANFIS controller. The range of the each
membership function presented in Fig. 4, as the figure
shows small is a trapezoidal function with the ranges:
[−1, −1, 10, 20], medium is triangular one with the
range: [10, 20, 30], and large is also trapezoidal func-
tion with the range: [20, 30, 500, 500].
We consider a scenario with 1,200 cars in one hour
simulation time. Fig. 3 shows the convergence trend
of genetic algorithm to find the optimal parameters
for ANFIS controller. It shows that the optimization
algorithm finds the optimal membership parameters
in about 20 generations.
An GA-FLC (Araghi et al., 2014) is also imple-
mented as a benchmark. Similar membership func-
tions are designed for GA-FLC Fig. 4. GA-FLC has
fixed parameters for its four inputs but parameters of
the output membership functions are adjusted using
the training method. In the case of fixed-FLC parame-
ters of all inputs and output are fixed and pre-defined.
The parameters of inputs membership functions are
similar to ANFIS and GA-FLC Fig.4, and the param-
eters of the output for fixed-FLC after training pre-
ANFISTrafficSignalControllerforanIsolatedIntersection
177

0 5 10 15 20 25 30 35 40
0
0.2
0.4
0.6
0.8
1
Q1
Degree of membership
Small Medium Large
Figure 4: Membership functions of inputs for ANFIS, GA-
FLC, and fixed-FLC .
0 10 20 30 40 50 60 70 80
0
0.2
0.4
0.6
0.8
1
GreenTime
Degree of membership
Small Medium Large
Figure 5: Membership functions of output for fixed-FLC.
sented in Fig. 5.
In all controllers, the appropriate green time for
each phase is generated based on the queue length in
four links. ANFIS controller uses the rule base ob-
tained during training and GA-FLC and fixed-FLC
apply the same rule base that presented in our pre-
vious work (Araghi et al., 2014). Rule base is pre-
sented in table 1. It is defined in a way to consider
neighbors situations in green time proposing. Queue
length of vehicles at current link (CL), next link (NL),
second next link (2NL), and third next link (3NL) are
the factors considered in the rule base definition. For
example, the first rule is defined as this:
If CL is small, NL is small or medium or large,
2NL is small or medium or large, and 3NL is small
or medium or large, then Green Time is small.
Based on the research is done in (Araghi et al.,
2014), parameters of GA-FLC are optimally tunned
using genetic algorithm with the purpose of minimiz-
ing delay times. The genetic algorithm used has 30
populations for optimizing seven parameters of eleven
output membership functions. Fig. 6 shows the pa-
rameters of output membership functions after train-
Table 1: FLC Rule Base. In this table S stands for small,
M for medium, L for large, and ∼ is for negation (eg., ∼S
means not-small, which could be either medium or large)
(Araghi et al., 2014).
CL NL 2NL 3NL Green Time
(1) S S/M/L S/M/L S/M/L S
(2) M S ∼M ∼M S
(3) M M M M M
(4) M L S/M/L S/M/L M
(5) L ∼L ∼L ∼L M
(6) L L ∼L ∼L L
(7) L ∼L L ∼L M
(8) L ∼L ∼L L M
(9) L ∼L L L M
(10) L L ∼L L L
(11) L L L ∼L L
(12) L L L L L
0 10 20 30 40 50 60 70 80
0
0.2
0.4
0.6
0.8
1
GreenTime
Degree of membership
Small Medium Large
Figure 6: Membership functions of the GA-FLC output af-
ter optimizing the parameters (Araghi et al., 2014).
ing with GA.
Fixed-time or pre-timed controller is usually used
as a benchmark for evaluating the performance of de-
signed controllers. In the fixed-time controller, a con-
stant amount of time is set for each phase. Consid-
ering constant time for each phase reduce the flexi-
bility of the fixed-time controller to adapt traffic de-
mands. The deigned fixed-time controllers use equal
time for all green phases. We have designed a fixed-
time controller with three different values as green
phase time: 20, 40, and 60 seconds values. This
is done to have a more comprehensive comparison
by considering three different values fixed-time con-
troller.
The performance of each controller is evaluated
by considering the total delay time of the intersection.
Fig. 7 shows the accumulative delay time of the inter-
section in a one-hour simulation after utilizing each
controller.
The diagram illustrates that the ANFIS controller
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
178
0 10 20 30 40 50 60
−0.5
0
0.5
1
1.5
2
2.5
x 10
4
Minute
Delay Time (sec)
ANFIS
GA−FLC
fixed−FLC
Fix20
Fix40
Fix60
Figure 7: Accumulative total delay time of the intersection
in one hour.
has a better performance than GA-FLC, fixed-FLC,
and fixed-time controller. Second best controller is
GA-FLC and then we have the fixed-FLC controller.
Fixed-time controller has a different result for each
green phase value. These differences prove that the
efficiency of the fixed-time controller is variable and
highly depends on the traffic conditions.
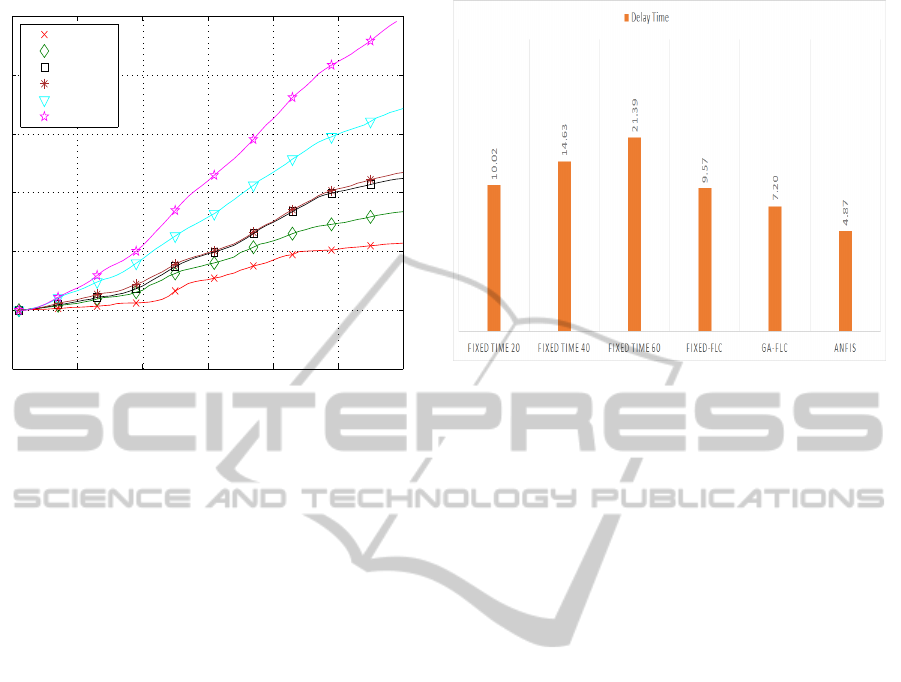
Fig. 8 shows the total delay that impose to the in-
tersection per vehicle in each hour. The bar chart also
shows that the best performance is achieved by AN-
FIS controller. It shows the amount of delay per vehi-
cle per hour for the intersection and these delay times
are presented in seconds. Fuzzy logic controllers
have totally better performance than fixed-time con-
troller. GA-FLC which is a version of fuzzy controller
with optimized output membership function parame-
ters obtains better result that fixed-FLC, and ANFIS
controller that has optimized rule base obtains the best
results between other controllers.
4 CONCLUSIONS
In this paper, we implement and examine the per-
formance of ANFIS for controlling traffic signals for
an isolated intersection. ANFIS gives the opportu-
nity of using fuzzy logic system in traffic signal con-
trolling while there is no need to pre-defined rule
base. Parameters of the ANFIS controller are opti-
mally tuned using genetic algorithm and ANFIS con-
troller obtains its optimal rule base. The purpose of
tuning and optimization is to minimize the total de-
lay in the network. GA-FLC (Araghi et al., 2014),
Figure 8: Total delay time per vehicle for the intersection.
a fuzzy controller with fixed and predefined param-
eters, and a fixed-time controller with three different
values are also designed and implemented to evalu-
ate the performance of the ANFIS controller. Trape-
zoidal and triangular membership functions are con-
sidered for queue lengths in fuzzy controllers. Re-
sults of the experiments for the simulation scenar-
ios show the better performance of the ANFIS con-
troller compared to two others fuzzy controllers and
fixed-time method. For our future work designing
and implementing fuzzy logic controllers for a multi-
intersection network has been planned. Considering
the situation of the neighbor intersections is a no-
ticeable factor in designing controllers for a multi-
intersection network.
REFERENCES
Abdoos, M., Mozayani, N., and Bazzan, A. (2011). Traf-
fic light control in non-stationary environments based
on multi agent q-learning. In 14th International
IEEE Conference on Intelligent Transportation Sys-
tems (ITSC), pages 1580–1585, Washington, DC,
USA.
Abdoos, M., Mozayani, N., and Bazzan, A. L. (2013).
Holonic multi-agent system for traffic signals con-
trol. Engineering Applications of Artificial Intelli-
gence, 26(56):1575–1587.
Araghi, S., Khosravi, A., and Creighton, D. (2014). Optimal
fuzzy traffic signal controller for an isolated intersec-
tion. In IEEE International Conference on Systems,
Man, and Cybernetics, page Under Publish.
Bazzan, A. L. C. (2009). Opportunities for multiagent sys-
tems and multiagent reinforcement learning in traf-
fic control. Autonomous Agents and Multi-Agent Sys-
tems, 18(3):342–375.
Cai, C., Wong, C. K., and Heydecker, B. G. (2009).
ANFISTrafficSignalControllerforanIsolatedIntersection
179

Adaptive traffic signal control using approximate dy-
namic programming. Transportation Research Part
C: Emerging Technologies, 17(5):456–474.
Chee, C. M. (2005). Cooperative, hybrid multi-agent sys-
tems for distributed, real-time traffic signal control.
PhD thesis, NUS, Singapore.
Chin, Y., Bolong, N., Kiring, A., Yang, S., and Teo, K.
(2011). Q-learning based traffic optimization in man-
agement of signal timing plan. International Jour-
nal of Simulation: Systems, Science and Technology,
12(3):29–35.
El-Tantawy, S., Abdulhai, B., and Abdelgawad, H. (2013).
Multiagent reinforcement learning for integrated net-
work of adaptive traffic signal controllers (MARLIN-
ATSC): methodology and large-scale application on
downtown toronto. IEEE Transactions on Intelligent
Transportation Systems, 14(3):1140–1150.
Favilla, J., Machion, A., and Gomide, F. (1993). Fuzzy traf-
fic control: adaptive strategies. In , Second IEEE In-
ternational Conference on Fuzzy Systems, 1993, pages
506–511.
Gartner, N. (1982). Demand-responsive decentralized ur-
ban traffic control: Part 1, single-intersection poli-
cies. Technical Report DOT/RSPA/DPB-50/81/24,
U.S. Department of Transportation, Office of Univer-
sity Research.
Gartner, N. H., Kaltenbach, M. H., and Miyamoto, M. M.
Demand-responsive decentralized urban traffic con-
trol: Part II, network extensions. Technical Report
DOT/RSPA/P-34/85/009, U.S. Department of Trans-
portation.
Hu, Y., Thomas, P., and Stonier, R. (2007). Traffic sig-
nal control using fuzzy logic and evolutionary algo-
rithms. In IEEE Congress on Evolutionary Computa-
tion, 2007. CEC 2007, pages 1785–1792. 00004.
Hunt, P., Robertson, D., and Bretherton, R. (1982). The
scoot online traffic signal optimisation technique.
Traffic Engineering and Control, 23(4):190–192.
Iqbal, M., Zahin, A., Islam, Z., and Kaiser, M. (2012a).
Neuro-fuzzy based adaptive traffic flow control sys-
tem. In 2012 International Conference on Commu-
nications, Devices and Intelligent Systems (CODIS),
pages 349–352.
Iqbal, M., Zahin, A., Islam, Z., and Kaiser, M. (2012b).
Neuro-fuzzy based adaptive traffic flow control sys-
tem. In 2012 International Conference on Commu-
nications, Devices and Intelligent Systems (CODIS),
pages 349–352.
Luk, J. (1984). Two traffic-responsive area traffic control
methods: SCATS and SCOOT. Traffic Engineering
and Control, 25(1):14–22.
Mirchandani, P. and Head, L. (2001). A real-time traffic
signal control system: architecture, algorithms, and
analysis. Transportation Research Part C: Emerging
Technologies, 9(6):415–432.
Nair, B. and Cai, J. (2007). A fuzzy logic controller for iso-
lated signalized intersection with traffic abnormality
considered. In 2007 IEEE Intelligent Vehicles Sympo-
sium, pages 1229–1233.
Niittymki, J. (2001). General fuzzy rule base for isolated
traffic signal controlrule formulation. Transportation
Planning and Technology, 24(3):227–247.
Pappis, C. P. and Mamdani, E. H. (1977). A fuzzy logic
controller for a traffic junction. IEEE Transactions on
Systems, Man and Cybernetics, 7(10):707–717.
Robertson, D. (1969). TRANSYT: a traffic network study
tool. Technical report, Road Research Laboratory,
Ministry of Transport, Crowthorne, Berkshire.
Schouten, S. (2007). Reinforcement Learning of Traffic
Light Controllers under Partial Observability. PhD
thesis, Faculty of Science University of Amsterdam,
The Netherlands.
Spall, J. C. and Chin, D. C. (1997). Traffic-responsive signal
timing for system-wide traffic control. Transportation
Research Part C: Emerging Technologies, 5(34):153–
163.
Udofia, K. and Emagbetere, J. (2013). Development of
multi-agent ANFIS-based model for urban traffic sig-
nal control. In 2013 International Conference on Con-
nected Vehicles and Expo (ICCVE), pages 662–669.
Vincent, R. A., Mitchell, A. I., and Robertson, D. I. c. .
User guide to TRANSYT version 8. Technical Report
LR888, Taffic Engineering Department, Transport and
Road Research Laboratory, Crowthorne, Berkshire,
U.K.
Wannige, C. T. and Sonnadara, D. U. J. (2009). Adaptive
neuro-fuzzy traffic signal control for multiple junc-
tions. In 2009 International Conference on Indus-
trial and Information Systems (ICIIS), pages 262–267.
00008.
Wei, W., Zhang, Y., Mbede, J., Zhang, Z., and Song, J.
(2001). Traffic signal control using fuzzy logic and
moga. In Proceedings of the IEEE International Con-
ference on Systems, Man and Cybernetics, volume 2,
pages 1335–1340. 00022.
Zeng, R., Li, G., and Lin, L. (2007). Adaptive traffic sig-
nals control by using fuzzy logic. In Second Interna-
tional Conference on Innovative Computing, Informa-
tion and Control, 2007. ICICIC ’07, pages 527–527.
00005.
FCTA2014-InternationalConferenceonFuzzyComputationTheoryandApplications
180
