Uncertainty Quantiﬁcation in Smart Grid Co-simulation Across

Heterogeneous Model Domains

Cornelius Steinbrink

OFFIS – Institute for Information Technology, Escherweg 2, 26121 Oldenburg, Germany

1 MOTIVATION

The international power distribution grids are ex-

pected to undergo fundamental restructuring in the

next decades, becoming Smart Grids. Smart Grids are

typically deﬁned as power grids enhanced with infor-

mation and communication technology (ICT). They

provide components of the power system with means

to send and receive information about current states,

energy requirements, load and generation predictions

etc. This calls for the development of various new

hardware devices and control concepts and thereby

for rigorous, systematic testing of the interaction be-

tween the new components.

Smart Grids are highly complex systems since

their dynamics do not solely depend on classical grid

components like generators and consumers anymore,

but also on weather predictions, market prices, the uti-

lization of the ICT system, and many other factors.

This complexity limits the pool of possible testing

procedures. Hardware experiments are too expensive

and inﬂexible to serve as generally applicable means

of testing. In the form of ﬁeld tests they are even

potentially dangerous since real infrastructure is in-

volved. Software simulation is considered to be more

suitable for the early stages of Smart Grid research

since it is generally cheap, ﬂexible and safe. However,

monolithic simulation software easily expires in its

usability since it does not consider the expendability

of the Smart Grid setup. Whenever new Smart Grid

components or concepts are introduced, they have to

be modeled and implemented by the software devel-

opers, which requires high manual effort and some-

times simply is not possible. In order to avoid this

overhead, the OFFIS – Institute for Information Tech-

nology, has developed the modular Smart Grid simu-

lation tool mosaik (Rohjans et al., 2013).

Mosaik is an event-based co-simulation frame-

work that allows the integration of existing Smart

Grid component models with the help of a ﬂexible

API. The implemented models exchange data with

one another via mosaik and may be instantiated and

orchestrated to form large-scale simulation scenarios

(i.e. scenarios with thousands of model instances).

The extensive scenario size is enabled at reasonable

computational costs by employing steady-state calcu-

lation of the grid utilization in the frequency domain

(e.g. PyPower, a port of the MATPOWER package

(Zimmerman et al., 2011)). This means that short-

term dynamic behavior like electro-magnetic tran-

sients is not resolved.

Due to its ﬂexible design, mosaik supports various

kinds of simulation processes, e.g. hardware emula-

tion. This is the concept of the Smart Energy Simula-

tion and Automation Laboratory (SESA-Lab) that has

been set up at the OFFIS. The central component of

the laboratory is the real-time simulator eMEGAsim

developed by the company OPAL-RT. This high per-

formance computer allows the simulation of network

models with µs resolution and provides digital and

analogue I/O capabilities that make it a ready-to-use

hardware-in-the-loop framework (HIL, see (de Jong

et al., 2011)). By combining mosaik and eMEGAsim,

the SESA-Lab enables analysis of dynamic transients

in precise subsystems of otherwise steady-state large-

scale scenarios. The main challenge of this approach

is to ensure accuracy of results for this heterogeneous

co-simulation system. A schematic overview of the

SESA-Lab setup is given in Figure 1.

2 STAGE OF THE RESEARCH

A showcase scenario has been implemented to

demonstrate the technical coupling between mosaik

and eMEGAsim. The scenario’s simulator pool con-

tains 44 low voltage grid nodes, 41 households, and

21 photovoltaic converters. The majority of these in-

stances is managed by mosaik. The included simula-

tors are based on time series and thus ensure power

generation and consumption within unproblematic

operational conditions. Similarly, no faults or power

outages have been modeled. Due to the simplicity of

this showcase it is a suitable starting point to system-

atically study the requirements for accurate coupling

Steinbrink C..

Uncertainty Quantiﬁcation in Smart Grid Co-simulation Across Heterogeneous Model Domains.

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Transformation

of Continuous

Data

Latency

Handling

Dynamic

Scheduling

Uncertainty

Quantification

Coupling

SESA-Lab

eMEGAsim

dynamic

mosaik

Simulator

Pool

steady-state

(e.g. PyPower)

Figure 1: Schematic sketch of the SESA-Lab concept.

between the two systems.

A theoretical list of these requirements has already

been set up and is presented in Section 3. The require-

ment, on which this PhD project is focused, is un-

certainty quantiﬁcation (UQ). It is the common way

to assess accuracy of measurements or simulation re-

sults. The challenges of designing a ﬂexible UQ sys-

tem in the Smart Grid context are discussed in Sec-

tion 4. A systematic design approach has been de-

veloped to tackle these challenges. The approach is

outlined in Section 6.

3 OUTLINE OF OBJECTIVES

The main objective of the presented PhD project is the

improvement of the coupling between eMEGAsim

and mosaik. Since the former represents a highly dy-

namic time domain system while the latter represents

a steady-state frequency domain system, information

is inevitably lost, which leads to uncertainty in the

results. Four requirements have been identiﬁed that

need to be fulﬁlled in order to reduce this uncertainty

as much as possible and provide a measure for the re-

sult accuracy: information transfer, latency handling,

dynamic scheduling, and, as mentioned before, uncer-

tainty quantiﬁcation.

The challenge of information transfer focuses on

the transformation of data. As already mentioned,

eMEGAsim calculates data in the time domain. Thus,

frequency domain transformation has to be performed

before sending data to mosaik. The simplest way

to do this is by calculating effective values of volt-

age and current, or via Fourier transform. However,

more elaborate techniques exist that support the goal

of preserving as much information as possible. No-

table concepts applied to power system analysis are

wavelet analysis (Shariatinasab et al., 2012), machine

learning (Wehenkel, 1997), and parameter estimation

(Lechtenberg et al., 2012). Choosing the most appro-

priate method or combination of methods for infor-

mation preservation is only one part of successful in-

formation transfer. It also has to be determined, in

which way mosaik (or implemented models) can ef-

fectively use this information. E.g. currently, there

is no component implemented in mosaik that is able

to process information about higher harmonics in the

eMEGAsim simulation. However, such components

might be integrated in the future. In that case, the

coupling between the platforms should provide usable

information in a standardized manner.

The issue of latency leads to temporal uncer-

tainty. First tests of coupling between mosaik and

eMEGAsim have revealed some transmission latency

for data exchange. Since the real-time simulator is

a closed-source resource, the transmission paths can

not be directly adjusted. However, different possi-

bilities exist to establish the connection between the

platforms. Therefore, the ﬁrst step to latency han-

UncertaintyQuantificationinSmartGridCo-simulationAcrossHeterogeneousModelDomains

dling is given by the systematic comparison of the

different connection strategies in order to ﬁnd the

one least inﬂicted with latency. Furthermore, a de-

terministic character of the latency has to be ensured.

Most likely, transmission latency can not be elimi-

nated completely. Instead, the remaining, determinis-

tic latency has to be quantiﬁed so that it can be com-

pensated or considered in some other way.

Scheduling is needed for the temporal speciﬁca-

tion of data exchange between the platforms, i.e. the

synchronization. Within mosaik scheduling is event-

based. Thus, data is exchanged whenever new val-

ues have been calculated through a simulation event.

This form of synchronization is very efﬁcient, but it is

not directly applicable to the coupling between mo-

saik and eMEGAsim. After all, the simulation of

eMEGAsim is continuous and therefore does not pro-

duce distinct events. The simplest alternative syn-

chronization mechanism is time-discrete with a ﬁxed

time interval between two “synchronization points”.

Lin and colleagues point out that this mechanism is

rather inefﬁcient since events that require data ex-

change do not necessarily coincide with the ﬁxed syn-

chronization points (Lin et al., 2011). If an important

event happens in between two synchronization points,

the corresponding system has to wait until the end of

the interval to send data. This leads to temporal uncer-

tainty. Of course, this uncertainty can be diminished

by reducing the time length between two synchroniza-

tion points. However, this would lead to much higher

computational effort. Instead, some previously dis-

cussed methods for data transformation may be used

to characterize and detect events in the eMEGAsim

signal. This would allow for much more efﬁcient

and accurate, event-based synchronization between

the platforms.

The presented requirements for accurate coupling

between mosaik and eMEGAsim are strongly con-

nected (see Figure 1). Elaborate information trans-

fer reduces uncertainty caused by information loss

and enables dynamic scheduling. Scheduling itself as

well as latency handling reduce temporal uncertainty.

Therefore, the three features provide the groundwork

for a UQ system that is then used to analyze the re-

maining inﬂuence of uncertainty in the Smart Grid

scenarios. Since the design of a UQ system is the

focus of this PhD project, the following sections out-

line the corresponding research process further. The

three aforementioned features will be included in the

coupling in a rather prototypical fashion and reﬁned

in future research projects.

4 RESEARCH PROBLEM

It is challenging to design a general UQ system for a

ﬁeld of application as complex as the SESA-Lab. The

main reason for this is that UQ is a multi-step process

that requires interaction with the user. Therefore, it

can not be fully automated. First, initial information

has to be provided about uncertainty of system mech-

anisms and input values. Then these uncertainties are

propagated through the model(s) and ﬁnally the cal-

culated uncertainty of the results is presented to the

user as a basis for decision-making. Further problems

stem from the fact that there exists no single standard-

ized measure to quantify uncertainty. The methods for

uncertainty propagation are manifold as well. Nev-

ertheless, some categories exist that are helpful for

theoretical conceptualization as well as practical im-

plementation. Uncertainties are typically divided into

aleatory and epistemic.

Aleatory uncertainty is also called irreducible un-

certainty. It stems from natural ﬂuctuations in a sys-

tem that can be statistically described but not dimin-

ished. Examples for this are power production of

wind farms and solar panels, or power consumptions

of households. In practice, knowledge about sources

of aleatory uncertainty is typically assumed in the

sense that mean value, standard deviation and form

of the distribution are known.

Epistemic uncertainty is deﬁned as reducible un-

certainty. It stems from the lack of knowledge about

parameters, input values or the system in general.

Therefore, it can theoretically be reduced when more

knowledge is obtained, but it can never be excluded

completely, due to the nature of knowledge. Exam-

ples for epistemic uncertainty are diverse: simpliﬁ-

cations in the model equations, the possibility of in-

tentional attacks against the system, or operation pa-

rameters of a power plant. In practice, the knowledge

about sources of epistemic uncertainty is by deﬁnition

sparse. Generally, only interval boundaries or mea-

sures from possibility theory are given. The coupling

features discussed in Section 3 all contribute to reduc-

ing epistemic uncertainty.

Methods for uncertainty assessment and propaga-

tion are oftentimes only appropriate to treat one of the

two types of uncertainty. Aside from that, they are di-

vided into intrusive and non-intrusive methods. Intru-

sive methods require the user to adjust the numerical

simulation code, e.g. to replace deterministic model

equations by stochastic ones. This leads to higher

computational efﬁciency since intrusive approaches

are not sampling-based. Non-intrusive methods leave

the model code untouched, which is sometimes less

efﬁcient but much more ﬂexible.

SIMULTECH2014-DoctoralConsortium

Since the SESA-Lab is a modular environment,

used by many stakeholders and practitioners of dif-

ferent backgrounds, non-intrusive UQ methods are

deemed the most appropriate. Intrusive methods

would require too much manual effort of the user, and

are not applicable at all when closed-source software

is used.

Additionally to being non-intrusive, UQ meth-

ods must sufﬁce two requirements for the SESA-Lab:

they must be computationally efﬁcient in order to be

applicable in large-scale scenarios, and they must be

applicable for sources of aleatory as well as epistemic

uncertainty. Combining these two requirements un-

derlines the challenging character of UQ in Smart

Grids. Computationally efﬁcient algorithms typically

assume knowledge about the distribution of uncertain

values and are therefore only applicable for aleatory

uncertainty, see e.g. (Lin et al., 2014). Distribution-

ignorant methods, on the other hand, are typically

sampling-based, like Monte Carlo Simulation (MCS),

which leads to high computational costs in complex

systems.

5 STATE OF THE ART

Uncertainty quantiﬁcation in general is a broad and

active research ﬁeld. Since it is a collection of widely

applicable methods, it is of interest for every scien-

tiﬁc discipline that is associated with measurement or

modeling. Consequently, readily usable tools have

been developed to facilitate the application of UQ

methods. One of the most noteworthy of these tools

is the open-source software DAKOTA (Adams et al.,

2014) that has been developed by Sandia National

Laboratories. It provides not only functionalities for

UQ but also for optimization, parameter estimation

and sensitivity analysis. The UQ capabilities of the

software include different ways to assess initial un-

certainty as well as the most established propagation

methods. However, it is not considered suitable to

manage mosaik’s UQ via DAKOTA by coupling the

platforms. The most important argument against the

coupling is the fact that the analyzed simulation code

has to be started by DAKOTA. This would limit the

independence and thereby the modular character of

mosaik. Furthermore, DAKOTA is not a domain-

speciﬁc tool. In the context of Smart Grid research,

it provides a large overhead of unnecessary function-

alities while those functions are not included that have

been speciﬁcally developed for the energy domain,

e.g. probabilistic load ﬂow (Borkowska, 1974). Nev-

ertheless, DAKOTA has to be considered as an im-

portant reference and a possible resource. After all,

the open-source character of the software promises to

be helpful for individual implementations of selected

methods.

Although UQ is a ﬁeld with a long tradition, its

application to power system modeling and especially

Smart Grid modeling has only started to gain atten-

tion in the recent years. It has often been suggested

that large-scale power systems are too complex for

classical sampling-based UQ methods like MCS. In-

stead, new methods are developed and improved, e.g.

the approach by Lin and colleagues (Lin et al., 2014).

They speciﬁcally test their collocation method with a

power grid model and demonstrate its computational

efﬁciency in comparison to MCS.

Hiskens and Alseddiqu present a UQ approach

speciﬁcally focused on dynamic, continuous power

system simulations, similar to the ones conducted

by eMEGAsim in the SESA-Lab context (Hiskens

and Alseddiqu, 2006). They point out the compu-

tational efﬁciency of their trajectory sensitivity ap-

proach, stressing the importance of this feature for

systems as complex as power grids.

The Smart Grid concept increases the complexity

of power systems even more, especially in the con-

text of uncertainty, as suggested by Zio and Aven (Zio

and Aven, 2011). They argue that the large amount

of determining factors yields different forms of un-

certainty due to different states of knowledge. This

is problematic since uncertainty propagation methods

oftentimes rely on knowledge about the uncertainty

sources. Furthermore, they deem it important to con-

sider as much uncertainty sources as possible, but it

can be difﬁcult even for experts to assess input uncer-

tainties for some sources, e.g: what is the probabil-

ity of a fault in a newly developed grid component?

Zio and Aven suggest a general framework for uncer-

tainty assessment in Smart Grids, divided into three

abstract categories, namely “drivers” (observable tar-

gets, e.g. costs), “limiters” (constraints, e.g. limita-

tions in technical deployment), and “effectors” (inﬂu-

encing phenomena, e.g. failures). However, the prac-

tical use of such a framework has not yet been tested.

In the context of mosaik, it is also unclear whether the

framework can be applied to each type of model that

is capable of being integrated through the API.

Li and Zio suggest a more practical approach

for joint assessment of uncertainties from different

sources (Li and Zio, 2012). They combine concepts of

probability and possibility theory in order to account

for different states of knowledge. However, they use

this approach as a ﬁrst step of MCS that is oftentimes

assumed to be unﬁt for complex, large-scale systems,

as stated above. It is questionable whether the joint

assessment approach is compatible with more sophis-

UncertaintyQuantificationinSmartGridCo-simulationAcrossHeterogeneousModelDomains

ticated propagation methods.

Uncertainty assessment is also the focus of some

auxiliary software tools for energy management sys-

tems. An example is a tool for the assessment of wind

power and load forecast uncertainty developed by

the Paciﬁc Northwest National Laboratory (Makarov

et al., 2010). It is a complex system in itself and con-

tains various methods for uncertainty assessment, e.g.

statistical analysis of error data. Still, it is worth con-

sidering to include specialized tools like this or se-

lected underlying concepts into the mosaik UQ frame-

work.

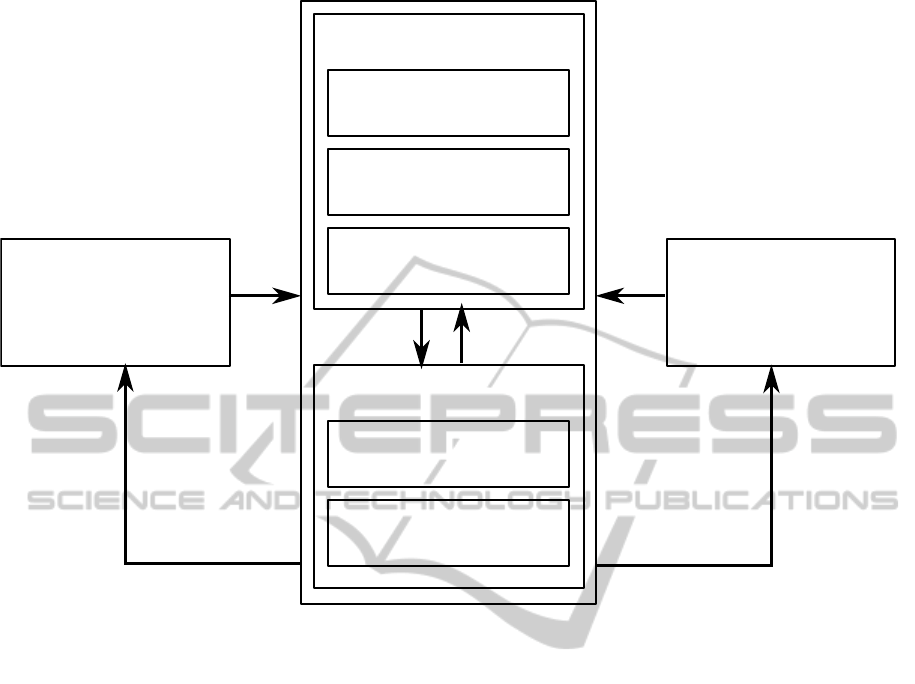
6 METHODOLOGY

The presented approach to set up a UQ system is

structured according to the design science frame-

work for information system research established by

Hevner and colleagues (Hevner et al., 2004), see Fig-

ure 2. They propose a number of guidelines that help

to set up the research project. In this sense, the UQ

system represents the artifact that is to be designed

(Guideline 1). The requirements are established by

a speciﬁc environment, i.e. users of the SESA-Lab,

and a knowledge base, i.e. literature regarding UQ

(Guideline 2). Furthermore, means of evaluation of

the artifact are needed (Guideline 3). For this, two

data and information sets will be set up: an uncer-

tainty taxonomy and a set of test scenarios.

A taxonomy is a common classiﬁcation scheme in

knowledge engineering that enables the practical han-

dling of theoretical concepts, see e.g. (Avi

zienis et al.,

2004). It collects the deﬁnitions of the concepts of

a certain domain and captures the relations between

them thereby facilitating the modeling of said con-

cepts. An uncertainty taxonomy in this sense is a

collection of all common uncertainty concepts that il-

lustrates how these concepts are represented and uti-

lized in practice. This establishes standardization and

is thus important for all steps of the UQ process that

require user interaction.

A second helpful data set consists of test scenar-

ios. Scenario-based design is a popular engineer-

ing approach in computer science that provides some

beneﬁts like early evaluation of usability of certain

concepts (Rosson and Carroll, 2002). In a practi-

cal sense, scenario sets furthermore provide different

types of boundary conditions for systematic testing

of implementations. The approach is typically itera-

tive with rough initial scenarios that become reﬁned

through theoretical and practical requirement analy-

sis. Smart Grid scenarios vary in size, types of inte-

grated grid components, and simulated faults. Addi-

tionally, SESA-Lab scenarios vary in the size of the

subsystem that is modeled in eMEGAsim. The show-

case scenario already counts as a ﬁrst test scenario

that now has to be complemented by other setups.

Once the taxonomy and test scenarios are set up,

they will be used to design and evaluate the artifact,

i.e. a UQ system for the SESA-Lab. A UQ system, as

outlined in Section 4, consists of three components:

an assessment framework for speciﬁcation of initial

uncertainties, a propagation method, and result repre-

sentation for the ﬁnal accuracy assessment.

An uncertainty assessment framework should pro-

vide users with the possibility to specify initial un-

certainties of different scenario components in a stan-

dardized manner. The differentiation between epis-

temic and aleatory uncertainty is important here. It

will be facilitated by the outlined uncertainty taxon-

omy.

Once the initial uncertainties are assessed, they

are propagated through the models via an appropri-

ate method. Since a variety of these methods is avail-

able, it has to be researched, which of them are ap-

plicable or adoptable in the SESA-Lab context and

thus should be included into the UQ system. Further-

more, it is promising to enhance sampling-based UQ

methods with practices from the ﬁeld of Design of Ex-

periments (DoE). DoE provides many techniques that

render sampling more efﬁcient and thereby minimize

the number of needed samples. DoE minimal sam-

pling methods like Latin Hypercube Sampling (LHS,

see (Giunta et al., 2003)) are already well-established

in UQ. The set of test scenarios will allow for system-

atic comparison of propagation methods.

Finally, the calculated uncertainty of the simula-

tion results has to be presented to the user in an efﬁ-

cient and understandable way in order to support in-

terpretation and decision-making. Since this task is

related to the assessment of initial uncertainties, the

taxonomy will again be helpful.

Validation of the UQ system artifact will be con-

ducted via use of the test scenarios. Uncertainty val-

ues may be computed for ﬁxed model compositions

a priori, even with methods that are not applicable in

the UQ system itself, e.g. intrusive methods. Then

these values are compared with the UQ system out-

put in order to evaluate its accuracy. It is reasonable

to select well-understood models for the test scenar-

ios so that correct uncertainty values can be identiﬁed

easily.

SIMULTECH2014-DoctoralConsortium

Assessment

Framework

Propagation

Method(s)

Result

Representation

Artifact: UQ System

Taxonomy

Test-Scenarios

Evaluation

Assess

Refine

Environment

Users of the

SESA-Lab

Knowledge Base

Literature

Research

Refine

Requirement

Analysis

Additions to the

Knowledge Base

Figure 2: Design process for the uncertainty quantiﬁcation system analogous to the framework proposed by (Hevner et al.,

2004).

7 EXPECTED OUTCOME

The expected outcome of the presented PhD project

is a coupling between the simulation platforms

eMEGAsim and mosaik with quantiﬁable accuracy.

This will contribute to the development of the SESA-

Lab, a setup for software/hardware as well as steady-

state/dynamic Smart Grid co-simulation. The cou-

pling ensures accuracy by reducing temporal and

data value uncertainty through means of latency han-

dling, dynamic scheduling, and data transformation.

The remaining uncertainty is quantiﬁed via a ﬂexible

UQ system that provides the user with standardized

means of interaction and readily evaluated propaga-

tion methods.

ACKNOWLEDGEMENT

The author would like to thank Prof. Sebastian Lehn-

hoff for valuable discussions, proofreading, and gen-

eral supervision of the PhD project. Further thank

goes to the SEE PhD program of the University of

Oldenburg for the possibility of pursuing the PhD.

REFERENCES

Adams, B. M., Ebeida, M. S., Eldred, M. S., Jakeman,

J. D., Swiler, L. P., Bohnhoff, W. J., Dalbey, K. R.,

Eddy, J. P., Hu, K. T., Vigil, D. M., Bauman, L. E.,

and Hough, P. D. (2014). Dakota, A Multilevel Paral-

lel Object-Oriented Framework for Design Optimiza-

tion, Parameter Estimation, Uncertainty Quantiﬁca-

tion, and Sensitivity Analysis. Sandia National Lab-

oratories, P.O. Box 5800, Albuquerque, New Mexico

87185, 5.4 edition.

Avi

zienis, A., Laprie, J.-C., Randell, B., and Landwehr, C.

(2004). Basic concepts and taxonomy of dependable

and secure computing. IEEE Transactions on Depend-

able and Secure Computing.

Borkowska, B. (1974). Probabilistic load ﬂow. IEEE Trans-

actions on Power Apparatus and Systems.

de Jong, E., de Graaff, R., Vaessen, P., Crolla, P., Roscoe,

A., Lehfuß, F., Lauss, G., Kotsampopoulos, P., and

Gafaro, F. (2011). European white book on real-time

powerhardware-in-the-loop testing. Technical report.

Giunta, A. A., Wojtkiewicz Jr., S. F., and Eldred, M. S.

UncertaintyQuantificationinSmartGridCo-simulationAcrossHeterogeneousModelDomains

(2003). Overview of modern design of experiments

methods for computational simulations. In 41st

Aerospace Sciences Meeting and Exhibit.

Hevner, A. R., March, S. T., Park, J., and Ram, S. (2004).

Design science in information systems research. MIS

Quarterly.

Hiskens, I. A. and Alseddiqu, J. (2006). Sensitivity, approx-

imation, and uncertainty in power system dynamics.

IEEE Transactions on Power Systems.

Lechtenberg, M., G

orner, K., G

otze, J., and Rehtanz, C.

(2012). Estimation of oscillation parameters for power

grids. In IEEE Asia Paciﬁc Conference on Circuits

and Systems.

Li, Y. and Zio, E. (2012). Uncertainty analysis of the ad-

equacy assessment model of a distributed generation

system. Renewable Energy.

Lin, G., Elizondo, M., Lu, S., and Wan, X. (2014). Uncer-

tainty quantiﬁcation in dynamic simulations of large-

scale power system models using the high-order prob-

abilistic collocation method on sparse grids. Interna-

tional Journal of Uncertainty Quantiﬁcation.

Lin, H., Sambamoorthy, S., Shukla, S., Thorp, J., and Mili,

L. (2011). Power system and communication network

co-simulation for smart grid applications. In Innova-

tive Smart Grid Technologies.

Makarov, Y. V., Huang, Z., Etingov, P. V., Ma, J., Gut-

tromson, R. T., Subbarao, K., and Chakrabarti, B. B.

(2010). Incorporating Wind Generation and Load

Forecast Uncertainties into Power Grid Operations.

Paciﬁc Northwest National Laboratory.

Rohjans, S., Lehnhoff, S., Sch

utte, S., and Scherfke, S.

(2013). mosaik – a modular platform for the eval-

uation of agent-based smart grid control. In 4th

IEEE/PES Innovative Smart Grid Technologies Eu-

rope.

Rosson, M. B. and Carroll, J. M. (2002). Scenario-based de-

sign. In The Human-Computer Interaction Handbook:

Fundamentals, Evolving Technologies and Emerging

Applications. Lawrence Erlbaum Associates.

Shariatinasab, R., Akbari, M., and Rahmani, B. (2012). Ap-

plication of wavelet analysis in power systems. In Ad-

vances in Wavelet Theory and Their Applications in

Engineering, Physics and Technology. InTech.

Wehenkel, L. (1997). Machine learning approaches to

power-system security assessment. IEEE Expert.

Zimmerman, R. D., Murillo-S

anchez, C. E., and Thomas,

R. J. (2011). Matpower: Steady-state operations, plan-

ning, and analysis tools for power systems research

and education. IEEE Transactions on Power Systems.

Zio, E. and Aven, T. (2011). Uncertainties in smart grids

behavior and modeling: What are the risks and vul-

nerabilities? how to analyze them? Energy Policy.

SIMULTECH2014-DoctoralConsortium