
Combining Different Computational Techniques in the Development
of Financial Prediction Models
A. J. Hoffman
School of Electrical, Electronic and Computer Engineering, North-West University, Potchefstroom, South Africa
Keywords: Neural Networks, Linear Regression, Histograms, Financial Time Series, Prediction, Portfolio Management.
Abstract: The prediction of financial time series to enable improved portfolio management is a complex topic that has
been widely researched. Modelling challenges include the high level of noise present in the signals, the
need to accurately model extreme rather than average behaviour, the inherent non-linearity of relationships
between explanatory and predicted variables and the need to predict the future behaviour of a large number
of independent investment instruments that must be considered for inclusion into a well-diversified
portfolio. This paper demonstrates that linear time series prediction does not offer the ability to develop
reliable prediction models, due to the inherently non-linear nature of the relationship between explanatory
and predicted variables. It is shown that the results of histogram based sorting techniques can be used to
guide the selection of suitable variables to be included in the development of a neural network model. We
find that multivariate neural network models can outperform the best models using only a single explanatory
variable. We furthermore demonstrate that the stochastic nature of the signals can be addressed by training
common models for a number of similar instruments which forces the neural network to model the
underlying relationships rather than the noise in the signals.
1 INTRODUCTION
The prediction of financial time series is a topic that
has been widely researched (Fama and French,
2008; Altay et al, 2005, Alcock et al, 2005 and
many others). Modelling the future behaviour of
financial time-series is a non-trivial task as the
process of the formation of market prices is
influenced by many factors, some of these being
unknown to the researcher, making it impossible to
construct an exact model based on known
underlying relationships. To a large extent an
empirical process must therefore be followed.
Many techniques have been developed for the
fitting of empirical models to complex data sets,
including multiple regression and neural networks
(Bishop, 1996). In the case of financial time series
this is complicated by several factors. Firstly it is
not known which explanatory variables would be the
most suited amongst a large set of candidates. It is
however of critical importance to limit the model
inputs to the smallest possible number, as all
empirical modelling techniques suffer from the
‘curse of dimensionality’ (Bishop, 1995) – too many
input variables translate into too much modelling
capacity, resulting in a model that is fitted to the
noise in the training set and that do not generalize
well in an out-of-sample test set.
The second challenge is closely related to the
first: in order to ensure good generalization
properties the number of observations available in
the training set must be large compared to the
number of degrees of freedom offered by the model.
The number of training samples available for a
single financial instrument may however be limited:
one may be limited to training sets with less than
100 samples per instrument, as explained later in this
paper. If a multivariate neural model is trained the
number of degrees of freedom may be more than 50;
given the noisy nature of the signals a model trained
on so little data is almost guaranteed to train mostly
on the noise in the training set and hence not to
generalize well outside of the training set.
A third challenge is the fact that, in the case of
portfolio return maximization, one needs to select
those investment instruments that will display
extreme return behaviour. As regression techniques
tend to model the average behaviour of input-output
relationships, the accuracy of such a model may be
very bad for extreme behaviour, specifically if the
276
Hoffman A..
Combining Different Computational Techniques in the Development of Financial Prediction Models.
DOI: 10.5220/0005136502760281
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 276-281
ISBN: 978-989-758-054-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

relationship is not linear, as will be demonstrated
through an example later in this paper.
Some of the most consistent techniques for
selecting investment instruments are based on
histogram techniques that involves the ranking and
sorting of instruments with respect to one or more
explanatory variables (Fama and French, 2008).
While this approach has the benefit of simplicity and
of averaging out most of the noise in the time series
behaviour, it is limited to the modelling of simple
relationships and to the use of only a small number
of simultaneous input variables.
Results claimed for the successful application of
linear regression and neural network techniques to
financial time series have mostly been applied either
to a small number of instruments or to the modelling
of stock indices only (e.g. Altay et al); such results
may however not work equally well to support a
portfolio management approach that requires the
modelling of a large number of instruments to be
considered for return maximization combined with a
sufficient level of diversification.
There is hence a need to develop a technique for
reliably modelling the expected return behaviour of
a large number of individual instruments, typically
all stocks listed on an exchange. It is the purpose of
this paper to demonstrate a method that combines
the capabilities of several modelling techniques and
that can represent general return behaviour observed
on an exchange.
The rest of the paper is organized as follows:
section 2 provides a brief literature survey, while
sections 3 and 4 describe the results obtained using
histogram and linear regression techniques. In
section 5 we describe the methodology used to
develop a neural network model that overcomes
several of the limitation of the prior techniques.
Section 6 provides an overview of the most
important results obtained, while section 7 concludes
and makes recommendations about future work.
2 LITERATURE OVERVIEW
There has been much fundamental debate in
literature about the predictability of financial time
series, and more specifically of stock returns (Blasco
et al, 1997; Kluppelberg et al, 2002). Initial views
in favour of the efficient market hypothesis stated
that stock prices already reflect all available
knowledge about that stock, making the prediction
of stock returns to earn abnormal returns on a
portfolio impossible in principle. Much has
however been published in recent years confounding
those early views, and today it is widely accepted
that the strong form of market efficiency does not
hold up in practice (Fama and French, 2004).
Many studies have demonstrated the ability of
both linear and non-linear time series prediction
models to predict future stock behaviour, contrary to
earlier beliefs that the market behaviour should be
described as a random walk model (Lorek et al,
1983; Altay and Satman, 2005; Bekiros, 2007; Jasic
and Wood, 2004; Huang et al, 2007).
3 HISTOGRAM TECHNIQUES
The most direct approach to uncover the ability of an
explanatory variable to predict future returns is to
sort the available set of instruments based on the
value of the explanatory variable. This technique
has been used successfully by Fama and French
(2008) to identify a set of fundamental and technical
variables that can explain so-called anomalous
future stock returns. The technique involves the
periodic ranking of stocks based on the values of
each of the explanatory variables. The ranked stocks
are then sorted into a number of bins and the average
returns of the stocks in each bin are calculated to
provide periodic sorted returns for the set of stocks
under consideration. The set of sorted returns
effectively represents the histogram of returns with
respect to the sorting variable.
Based on previous results (Hoffman, 2012) we
considered the following set of sorting variables:
MC (log of market capitalization);
One month return over last month (Ret1(-1);
Momentum (12 month accumulated returns);
BtoM (book-to-market equity ratio);
DO (detrended oscillator, variable used to detect
the onset of upward or downward movements);
1 month (Ret1_Sector) and 12 month
(Ret12_Sector) returns of the sector from which
the stock originated.
Results obtained with the sorting of stocks listed
on the Johannesburg Stock Exchange (JSE) using 5
sorting bins are shown in table 1 below. By
calculating the t-statistics of the sorted returns it can
be determined whether the deviations in returns
between bins are statistically significant. If a hedged
portfolio is formed long positions will be taken in
stocks in the highest sorted bin and short positions
for stocks in the lowest sorted bin.
CombiningDifferentComputationalTechniquesintheDevelopmentofFinancialPredictionModels
277

Table 1: Sorted monthly returns of explanatory variables.
SortedBin
1 2 3 4 5
MC
0.76% 0.21% 0.48% 0.51% 0.08%
Momentum
‐0.60% 0.05% 0.31% 0.62% 1.56%
Ret1(‐1)
0.64% 0.59% 0.84% 0.77% 1.19%
BtoM
‐0.48% 0.13% 0.69% 0.42% 1.22%
YtoB
‐0.42% 0.48% 0.90% 0.60% 0.45%
DO_Value
‐0.62% 0.08% 0.27% 0.82% 1.39%
DO_Ret
‐0.42% 0.33% 0.47% 0.64% 0.95%
R1_Sector
‐0.11% 0.15% 0.28% 0.59% 1.06%
R12_Sector
‐0.05%‐0.10% 0.41% 0.78% 0.94%
Histograms rely on the averaging effect over all
sorted items to eliminate noise specific to individual
item properties and to retain only common aspects
of behaviour; an accurate reflection of the
underlying relationship is obtained only if there are a
significant number of items in each sorted bin. On a
smaller exchange like the JSE the total number of
listed stocks is approximately 400. Should two
sorting variables and five bins be used the number of
items in each of the 25 bins will be approximately
16, which is already marginal in terms of the
standard deviation of the sorted means. This
demonstrates the inherent limitation of the histogram
technique to be used as multivariate model.
4 LINEAR REGRESSION
Linear regression is probably the most widely used
modelling technique to uncover empirical
relationships; it provides consistent results as, in
contrast to neural networks, exact statistical
formulas can be used for extracting the values of
linear regression coefficients that e.g. minimize the
sum-of-squared modelling errors. In the case of
financial time series different versions of so-called
ARMAX techniques can be used as a special version
of linear regression, with the ARMAX model chosen
depending of the type of autoregressive and moving
average relationships that are included into the
model, and whether extraneous variables are
included or not.
While linear regression has significant appeal
due to its simplicity, consistency and the limited
computational effort required to extract the linear
regression coefficients, it is limited to the modelling
of linear relationships. We will demonstrate the
fitting of a linear regression model to an inherently
non-linear relationship that was uncovered by a
sorting method, resulting in linear regression
predictions that are counter-productive.
Table 2 below provides results for the sorting of
1 month future returns using 12 month historic
returns as sorting variable. The sorting technique
produces a very useful hedge return of 1.82% on
average per month. The size of the t-statistics for
extreme bins also indicates a statistically significant
relationship. It can be seen that, while there is not a
strong relationship between input and output over
bins 2 to 4, the relationship seems to bend strongly
up- and downwards in bins 2 and 1 respectively,
indicative of a non-linear relationship. We extract a
linear regression model using 12 month historic
returns as input and one month future returns as
output variable and calculate the predicted and
residual returns, the latter defined as the difference
between the actual and predicted returns. By sorting
the stocks based on predicted returns we calculate
the average returns and residual predicted returns
within each sorted bin, as displayed in table 3 below.
Table 2: Sorted monthly returns using 12 monthly historic
returns as sorting variable.
BinNo 1 2 3 4 5
AveRet‐0.08% 0.60% 0.76% 0.98% 1.74%
tStat‐5.52‐1.34‐0.34 1.02 5.73
High‐Low 1.82%
Table 3: Sorted monthly returns and residual returns using
linear regression based predicted returns as sorting
variable.
BinNo 1 2 3 4 5
AveRet% 0.69 1.02 0.53 1.03 0.80
tStat‐0.77 1.27‐1.77 1.38‐0.09
High‐Low% 0.11
ResPredRet% 6.6 2.0‐0.1‐1.0‐4.6
tStat 42.8 12.7‐0.7‐6.3‐30.3
It can be seen that, in contrast to the direct
application of sorting to the explanatory variable, the
linear regression prediction produced almost zero
hedge returns. In this case the average linear
correlation between input and output variable was -
0.044, even though there is a strong positive
correlation between input and output for items in the
extreme bins. It is also clear that the residual returns
in the extreme bins have means that are distinctly
positive or negative respectively, which is indicative
of an inherently non-linear underlying relationship;
this is confirmed by the large t-statistics obtained in
the extreme bins. This simple example demonstrates
the limitations of using linear models to financial
time series prediction.
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
278

5 DEVELOPING A NEURAL
NETWORK MODEL
The most popular technique for modelling non-
linear empirical relationships is neural networks
(NNs), based on their ability to model relationships
of arbitrary nature using small number of model
parameters (Bishop, 1996). A number of key
decisions have to be made as part of the NN
development process. The first of these is to decide
whether to develop a separate NN for each
instrument, one NN for all instruments or a separate
NN for each category of instruments that are
believed to display similar behaviour. A second
decision involves the selection of input variables; as
the number of model inputs impacts the number of
degrees of freedom, and given the limited number of
training observations and the need to generalize
outside of the training set, this decision is closely
link to the first. A third decision is the length of
time history to be included into the training set:
making the training set as large as possible in order
to reduce the impact of noise may not be optimal in
other respects, as the underlying nature of the
relationships to be modelled may change over time.
The above choices depend on the available number
of training observations, the strength and stability of
the expected relationships and the degree to which it
is expected that different instruments will display
common behaviour. The expected complexity of the
relationships will dictate the neural architecture to be
implemented. The stability of the relationships
should determine the time span of training sets.
It is clear that there are a significant number of
options to choose from, resulting in a potentially
very large number of model permutations. Given
the relatively lengthy process to train a NN (which
typically includes training several networks for each
permutation, given the stochastic nature of the NN
training process) it is not practically possible to
exhaustively experiment with all possibilities. A
more productive approach is use sorting and linear
regression techniques to select those variables that
show potential for inclusion into a set of NN inputs,
and to determine the presence of non-linearities in
the relationships.
For the purpose of this exercise we considered
those candidate inputs that were found to possess
significant explanatory power to predict one month
returns based on ranking and sorting. We selected
market capitalization (MC) and book-to-market ratio
(BtoM) as the fundamental variables with the most
prominent explanatory power. In order to improve
upon the predictive abilities of these fundamental
inputs we considered several technical variables; at
monthly time scales the most prominent
relationships between past and future returns are
mean reversion in returns (Cubbins et al, 2006) and
momentum in returns (Fama and French, 2008). We
therefore add momentum and a detrended oscillator
to the set of inputs; the latter is a commonly used
technical indicator used to detect changes in the
current trend and that has been found to display
consistent positive relations with future returns
(Hoffman, 2012). We also add sector 1 and 12
month returns as additional extraneous variables.
In the case of JSE listed stocks we are limited to
less than 400 stocks at any given point in time, with
an available time history spanning between 20 and
25 years. We are therefore limited to maximum 250
to 300 monthly observations per stock. To allow the
calculation of variables like momentum, requiring a
history of 12 months, the training set must be further
reduced. In order to determine whether the model
development technique produces repeatable results
we furthermore have to repeat the model training
and prediction process over a period of at least 10
years to observe the impact of the different market
(bull and bear) cycles. It is hence clear that we will
be left with less than 100 training observations per
stock for every model training cycle. If we include 5
or more input features and several hidden nodes the
number of model degrees of freedom will range
between 30 and 60; 100 training samples is thus too
few to allow the extraction of a separate NN model
for each stock, given the stochastic nature of the
relationships to be modelled. We are therefore
forced to group stocks together in order to
accumulate sufficiently large training sets.
As observed from the sorted returns results, the
behaviour that should be profitable to exploit occurs
in the extreme sorted categories. We assist the
neural training process to focus primarily on extreme
behaviour by weighing the training sets unevenly:
we identify extreme observations (observations
where either the input or the target value falls into an
extreme sorted bin) and load the training set with a
disproportionate fraction of extreme observations to
ensure that ‘average’ observations will not dominate
the learning process.
For each model extraction cycle we select a
training set that spans over a maximum period of 5
years and construct a training set that contains
observations selected with equal probability from
the available time history of all stocks. A separate
test set is constructed using the same selection
techniques but spanning over a time period that
directly follows on the time period representing the
CombiningDifferentComputationalTechniquesintheDevelopmentofFinancialPredictionModels
279
training set. After training the model it is applied to
the training and test sets. The prediction results are
then allocated to the individual stocks so that the
predicted returns for each stock can be determined
for the next investment period. The predicted stock
returns are ranked and sorted and a hedge portfolio
is formed by going long in the highest sorted
category and short in the lowest sorted category.
The above process is repeated over the available
time window, and the average sorted return for each
bin over the available time period as well as the
hedge portfolio returns is calculated.
The success of this combined approach to model
development will be measured by comparing the
sorted returns generated by the prediction model
against the sorted returns generated by any of the
individual explanatory variables used in the original
sorted returns exercise, as well as with the results
obtained from using linear regression models.
6 RESULTS
We use stock returns calculated relative to a value
weighted market return – a model with no predictive
capability should therefore produce sorted returns
that do not significantly differ from zero. Variables
with hedged returns that are statistically significant
from zero are displayed in table 4 below.
Table 4: Sorted monthly hedged returns and t-statistics of
explanatory variables used as model inputs.
High‐Low H‐LtStat
MC ‐0.68% ‐4.7
Ret1(‐1) 0.55% 3.4
Momentum 2.16% 14.8
BtoM 1.71% 11.7
YtoB 0.87% 6.0
DO
_
Value 2.00% 13.7
DO_Ret 1.37% 9.4
Ret1_Sector 1.17% 8.0
Ret12
_
Sector 0.99% 6.8
Secondly we use the above set of variables as
inputs in a linear regression model to determine
whether a multivariate linear model can produce
predicted return results that are superior to the sorted
return results of the individual variables. The sorted
predicted returns and residual predicted returns are
displayed in table 5. It can be seen that the hedged
return produced by the linear regression model is
significantly lower than the hedged returns produced
by any of the variables used as regression inputs.
This failure of linear regression to capture the true
input-output relationship is confirmed by the large
residual returns in the extreme bins.
Table 5: Sorted monthly returns using linear regression
predicted returns as sorting variable.
SortedBin 1 2 3 4 5
AveRet% 0.32 0.08 0.37 0.40 0.70
tStat‐0.43‐2.08‐0.06 0.15 2.26
High‐Low% 0.39
H‐LtStat 2.69
ResPredRet% 12.9 2.0‐0.22‐2.0 12.5
tStat 94.52 14.68‐1.64‐14.6 91.50
Thirdly we develop neural network models using
the same set of input variables. We start with the
single input variable that produced the highest sorted
returns. Other variables are then considered for
addition; such additional variables are only retained
if the sorted hedged returns of the resulting
prediction model exceed that of the model excluding
that variable. We verify if the modelled
relationships display gradual changes over the range
of inputs values (as would be expected in practice),
rather than abrupt changes (as can easily be obtained
with neural models if insufficient regularization is
used). This was done by varying one input at a time
between its extreme values while maintaining the
other inputs at their average values. One of the
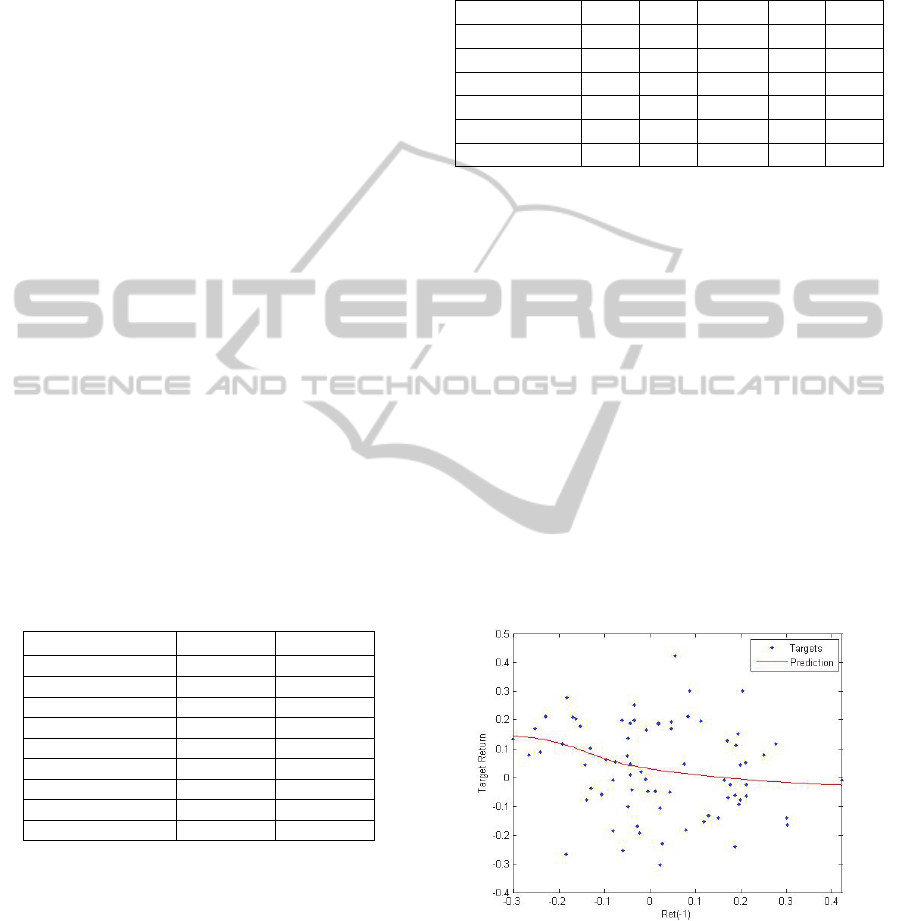
modelled relationships is displayed in figure 1 below
– the relationship, however nonlinear, display
gradual changes over the ranges of input values; this
provides additional confidence in the model.
Figure 1: Typical input-target variable scatter plot and
neural network prediction.
The sorted returns as well as the High-Low
hedged returns using the NN prediction as sorting
variable are displayed in table 6 below. It is clear
that the neural model produce results that are
superior to the results of any of the individual
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
280

explanatory variables. Whereas the largest average
monthly hedged return for a single variable is
2.15%, the best neural model produced hedged
returns of 3.35% per month, which translates to an
annual return of approximately 48% relative to the
market return. This is a very significant result, given
that in practice the best stock based investment
funds seldom outperforms the market by more than
8-10 % per annum. It can furthermore be seen that
the residual returns are spread much more evenly
across all sorted bins, in contrast to the results
obtained using linear regression. This means that
the neural network model was able to effectively
capture the inherent non-linearity in the input-output
relationships.
Table 6: Sorted monthly returns and residual returns using
neural network predicted returns as sorting variable.
SortedBin 1 2 3 4 5
AveRet%‐1.27 0.03 0.40 0.67 2.08
tStat‐11.37‐2.45 0.15 1.98 11.62
High‐Low% 3.35%
H‐LtStat 22.98
AveResRet%‐1.03‐0.71‐0.34 0.05 1.62
tStat‐7.57‐5.24‐2.48 0.39 11.87
7 CONCLUSIONS
In this paper we demonstrated the value of
combining several different computational
techniques in an integrated methodology. We
described the results that can be obtained by ranking
and sorting returns as well as by using linear
regression techniques, and demonstrated that while
being useful, both approaches have specific
limitations. We then combined these techniques
with neural networks to exploit the non-linearities in
the relationships that were uncovered. Neural
network models were trained taking into account the
fact that stocks are selected to exploit extreme rather
than average behaviour. The methodology was
subjected to rigorous testing for all stocks forming
part of the JSE and over a period of approximately
20 years. The resulting multivariate NN model
produced significantly superior results compared to
any of the variables on their own.
In contrast to earlier work our results represent
the performance obtained by equally considering all
stocks available on the JSE, using explanatory
variables that have been demonstrated before to each
possess predictive power in their own right, and
applying the same stock selection methodology over
a period of more than 20 years that contains several
bull and bear cycles. We can therefore conclude that
multivariate NN models can outperform single input
sorting techniques as well as multivariate linear
regression techniques. It is furthermore clear that
each important model development decision must be
based on a solid understanding not only of the
modelling techniques used but also of the
application domain, in this case portfolio
management.
Future work will involve the expansion of the
same methodology to different categories of stocks,
as well as to decision making on a daily rather than a
monthly basis.
REFERENCES
Alcock, J., Gray, P., June 2005. Forecasting stock returns
using model-selection criteria. In The Economic
Record, 81(253).
Altay, E., Satman, M. K., Stock market forecasting:
artificial neural network and linear regression
comparison in an emerging market, 2005. In Journal
of Financial Management and Analysis, 18(2).
Bekiros, S. D., 2007. A neurofuzzy model for stock
market trading. In Applied Economics Letters, Vol. 14.
Bishop, C. M., Neural networks for pattern recognition,
Clarendon Press, 1995.
Blasco, N., Del Rio, C., Santamaria, R., The random walk
hypothesis in the Spanish stock market: 1980-1992.
June 1997. In Journal of Business Finance and
Accounting, 24(5).
Cubbins E, Eidne M, Firer C and Gilbert E. 2006. Mean
reversion on the JSE. Investment Analysts Journal, 63:
39 – 48.
Fama, E. F., French, K. R., 2004. The Capital Asset
Pricing Model: Theory and Evidence. In Journal of
Economic Perspectives, 18(3).
Fama, E. F., French, K. R., August 2008. Dissecting
Anomalies. In The Journal of Finance, LXIII(4).
Hoffman, A. J., 2012, Stock return anomalies: evidence
from the Johannesburg Stock Exchange. In Investment
Analysts Journal, No. 75, pp. 17-37.
Huang, W. et al, 2007. Neural networks in finance and
economic forecasting. In International Journal of
Information Technology and Decision Making, 6(1).
Jasic, T., Wood, D. 2004. The profitability of daily stock
market indices trades based on neural network
predictions. In Applied Financial Economics, 14.
Kluppelberg, C. et al, 2002. Testing for reduction to
random walk in autoregressive conditional
heteroskedasticity models. In Econometrics Journal,
5, pp. 387-416.
Lorek, K. S. et al, 1983. Further descriptive and predictive
evidence on alternative time-series models for
quarterly earnings. In Journal of Accounting Research,
21(1).
CombiningDifferentComputationalTechniquesintheDevelopmentofFinancialPredictionModels
281
