Computationally Efficient Multi-Objective Optimization of and

Experimental Validation of Yagi-Uda Antenna

Adrian Bekasiewicz

, Slawomir Koziel

and Leifur Leifsson

Faculty of Electronics, Telecommunications and Informatics, Gdansk University of Technology, 80-233 Gdansk, Poland

Engineering Optimization & Modeling Center, Reykjavik University, Menntavegur 1, 101 Reykjavik, Iceland

Keywords: Antenna Design, Design Optimization, Multi-Objective Optimization, Electromagnetic Simulation,

Simulation-Driven Design, Design Space Reduction, Surrogate-based Optimization.

Abstract: In this paper, computationally efficient multi-objective optimization of antenna structures is discussed. As a

design case, we consider a multi-parameter planar Yagi-Uda antenna structure, featuring a driven element,

three directors, and a feeding structure. Direct optimization of the high-fidelity electromagnetic (EM)

antenna model is prohibitive in computational terms. Instead, our design methodology exploits response

surface approximation (RSA) models constructed from sampled coarse-discretization EM simulation data.

The RSA model is utilized to determine the Pareto optimal set of the best possible trade-offs between

conflicting objectives. In order to alleviate the difficulties related to a large number of designable

parameters, the RSA model is constructed in the initially reduced design space, where the lower/upper

parameter bounds are estimated by solving appropriate single-objective problems resulting in identifying the

extreme point of the Pareto set. The main optimization engine is multi-objective evolutionary algorithm

(MOEA). Selected designs are subsequently refined using space mapping technique to obtain the final

representation of the Pareto front at the high-fidelity EM antenna model level. The total design cost

corresponds to less than two hundred of EM antenna simulations.

1 INTRODUCTION

Contemporary antenna structures have to be

designed to satisfy very strict performance

requirements concerning various characteristics such

as reflection, gain (Sharaqa and Dib, 2013;

Koulouridis et al., 2007), cross polarization

(Afshinmanesh et al., 2008; Chamaani et al., 2011)

or side-lobe level (Kuwahara, 2005; Jin and Rahmat-

Samii, 2007). At the same time, antenna topologies

become more and more complex and their

electromagnetic (EM) models have to account for

various interactions with the environment (e.g.,

housing, connectors, installation fixtures, etc.).

Standard design procedures based on repetitive

parameter sweeps guided by engineering experience

are normally laborious and typically fail to find a

truly optimum results. On the other hand, automated

design using numerical optimization procedures

(e.g., Nocedal and Wright, 2006; Conn et al., 2009)

may be associated with prohibitively high

computational costs when accurate, high-fidelity EM

simulations are used for antenna performance

evaluation.

In general, antenna design is a multi-objective

process where various (often conflicting) objectives

have to be simultaneously accounted for (Kolundzija

and Olcan, 2006; Yang et al., 2008). The goal of

multi-objective optimization is normally to identify

a set of designs (also referred to as a Pareto-optimal

set) representing the best possible trade-offs between

non-commensurable objectives (Deb, 2001).

Compared to conventional single-objective

optimization, multi-objective design posed

additional challenges, both conceptual (due to

possible non-commensurability of vector-valued

objective function) and computational (related to the

necessity of identifying multiple solutions).

Conventional direct-search methods (including

gradient based algorithms) are not suitable for

solving multi-objective design tasks (Deb, 2001).

Population-based metaheuristic algorithms, such as

genetic algorithms (Ding and Wang, 2013; Junwei et

al., 2009; Koulouridis et al., 2007;) and particle

swarm optimizers (Chamaani et al., 2011; Jin and

798

Bekasiewicz A., Koziel S. and Leifsson L..

Computationally Efﬁcient Multi-Objective Optimization of and Experimental Validation of Yagi-Uda Antenna.

DOI: 10.5220/0005136607980805

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SDDOM-2014), pages

798-805

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Rahmat-Samii, 2007; Jin and Rahmat-Samii, 2010),

are more attractive because of their ability of finding

the entire representation of the Pareto set in a single

algorithm run (Deb, 2001). Unfortunately,

disadvantage of population-based search techniques

is their high computational cost which is a result of

processing large sets of candidate solutions – typical

number of objective function evaluations are a few

thousands to tens of thousands for a single algorithm

run (Afshinmanesh et al., 2008; Kuwahara, 2005).

This is a serious drawback when handling EM-

analyzed antenna models: simulation time for

realistic setups that take into account not only the

antenna structure itself but also its environment

(feeding structure, connectors, installation fixtures)

may take as long as a few hours per design.

Utilization of surrogate-based optimization

(SBO) techniques (Bandler et al., 2004; Koziel et

al., 2013) can alleviate the difficulities related to

high cost of metaheuristic optimization. In SBO

scheme, the high-fidelity antenna model is replaced

by a computationally cheap, yet less accurate

surrogate (a so-called low-fidelity model), which can

be 10 to 50 times faster than its high-fidelity

counterpart. In case of antennas, a surrogate is

usually a coarsely-meshed version of the high-

fidelity model, evaluated in the same

electromagnetic (EM) solver (Koziel et al., 2014;

Bekasiewicz et al., 2014a). The optimization burden

in SBO is shifted to a surrogate, which is iteratively

refined in a prediction-correction loop. The

numerical expenses related to massive evaluations of

the low-fidelity model during metaheuristic

optimization may be further reduced by

incorporation of response surface approximation

(RSA) techniques (Koziel and Bandler, 2012; Koziel

and Ogurtsov, 2013). However, the cost of RSA

model preparation grows exponentially with the

number of designable parameters, which reduces

potential applications of this approach to low-

dimensional antenna design cases only.

In (Koziel and Ogurtsov, 2013), a surrogate-

based multi-objective optimization scheme for

seeking the representation of a Pareto optimal-set

using population-based metaheuristics has been

proposed. The approach partially addressed the

problem of RSA model construction for antennas

with up to 8 geometrical parameters by means of

structure decomposition into a radiator and its

feeding network; however, this is not possible for

majority of modern antenna designs. Also,

decomposition is not practical when the number of

parameters in the decomposed parts is still too large.

In this work, we discuss a simple yet robust

methodology for design space reduction aimed at

generation of an accurate RSA model to extend the

applicability of the technique described in (Koziel

and Ogurtsov, 2013). Our approach is based on

identification of the extreme points of the Pareto set

by performing separate single-objective

optimizations with respect to each design goal, one

at a time. The reduced design space is a hypercube

determined by these extreme points and it is orders

of magnitude (volume-wise) smaller than the initial

one, which allows for a construction of an accurate

RSA model even for large number of design

variables. For the sake of demonstration, we

consider a 12-variable planar Yagi-Uda antenna

optimized with respect to minimum voltage standing

wave ratio (VSWR) and maximum average gain

within the frequency band of interest. A set of

designs selected from the Pareto set obtained

through optimization have been fabricated and

measured to experimentally validate the design

methodology.

2 MULTI-OBJECTIVE DESIGN

OPTIMIZATION

In this section, we recall the formulation of the

multi-objective optimization problem. We also

discuss the optimization algorithm as well as the

design space reduction scheme. In Sections 3 and 4,

our design methodology is demonstrated using a

planar Yagi-Uda antenna. Experimental validation is

provided in Section 5.

2.1 Formulation of Multi-Objective

Antenna Design Problem

We will denote by R

(x) as an accurate (or high-

fidelity) model of the antenna under optimization.

The model is obtained using EM simulation at fine

discretization. Antenna response (gain, side-lobe

level or VSWR) is denoted by R

, whereas x is a

vector of designable (normally, geometry)

parameters.

Let F

(x)), where k = 1, …, N

obj

, be a kth

objective. A typical design objective could be

related to minimization of an antenna side-lobe

level, reduction of the occupied area or

maximization of gain. In multi-objective scheme we

seek for a representation of a so-called Pareto

optimal-set X

, which is composed of non-

dominated designs such that for any x  X

, there is

ComputationallyEfficientMulti-ObjectiveOptimizationofandExperimentalValidationofYagi-UdaAntenna

799

no other design y for which the relation y  x is

satisfied (y  x, i.e., y dominates over x, if F

(y))

 F

(x)) for all k = 1, …, N

obj

, and F

(y)) <

(x)) for at least one k) (Deb, 2001).

For the sake of optimization we also consider a

coarse-discretization version R

of R

, referred to as

the low-fidelity model. R

is evaluated using the

same solver as R

and it is typically at least one order

of magnitude faster than the high-fidelity model.

2.2 Multi-Objective Optimization

Methodology

Both the high-fidelity model R

and its low-fidelity

(coarse-discretization) counterpart R

are too

expensive to be directly optimized in multi-objective

sense. For that reason, a kriging interpolation model

is prepared (Simpson et al., 2001) using a set of

training samples acquired by simulating R

at the

predetermined training locations (Koziel et al.,

2013). Here, the samples are distributed using Latin

Hypercube Sampling (LHS) algorithm (Beachkofski

and Grandhi, 2002) within the previously reduced

design space. The methodology for a solution space

reduction is briefly described in Section 2.3.

The main tool for identification of Pareto optimal

solutions is a multi-objective evolutionary algorithm

(MOEA) with fitness sharing, mating restrictions

and Pareto dominance tournament selection (Talbi,

2009). The solutions obtained by MOEA define the

initial approximation of the Pareto optimal-set of

interest. In the next stage, we select K designs from

the initial solution set: x

(k)

, k = 1, …, K. The chosen

designs are subsequently refined using SBO to find

their corresponding high-fidelity model R

responses. The description of the SBO scheme given

below assumes two design objectives: F

and F

;

however, the procedure can be easily generalized to

any number of objectives. For each x

(k)

, the

corresponding high-fidelity model solution x

(k)

found using the output space mapping (OSM)

algorithm of the form (Koziel et al., 2008):



(.)

(. 1)

(.) (.)

,() ( )

arg min ( ) [ ( ) ( )]

ki ki

sfsss









xx x

Rx Rx Rx

(1)

where x

(k.i)

is the ith approximation of x

(k)

(the

process (1) is iterated until convergence).

The objective of design refinement is to

minimize F

for each x

(k)

without degrading F

. The

utilization of OSM ensures perfect alignment of the

surrogate model R

with the high-fidelity model at

the beginning of each iteration of (1). Usually, 2 to 3

iterations are required to find the desired high-

fidelity model solutions x

(k)

. The OSM-driven

refinement procedure is repeated for all K chosen

samples. One should emphasize that the evaluation

of the high-fidelity model R

is performed only

during the refinement step. In this work, the

construction of kriging interpolation model is

performed using a DACE toolbox (Lophaven et al.,

2002). The block diagram of the optimization

procedure is shown in Fig. 1. More detailed

explanation of the optimization algorithm can be

found in (Koziel and Ogurtsov, 2013).

2.3 Design Space Reduction Algorithm

Response surface approximation model R

, once set

up, is very fast and easy to optimize; however the

cost of gathering training data for its construction

increases exponentially with the number of design

variables, which makes utilization of such a model

questionable if the number of antenna geometry

parameters is larger than 5 or 6 (Bekasiewicz et al.,

2014b; Koziel and Ogurtsov, 2013). Consequently,

the reduction of the design space is a crucial step to

make the RSA model setup feasible.

The Pareto optimal-set is usually located in a

small region of the initially defined design space:

normally, the frontiers for each geometry parameter

of an antenna are defined rather wide to ensure that

the desired solutions are located within these

prescribed limits.

Figure 1: Design flow of the proposed multi-objective

optimization procedure.

START

Reduce design space

Refine selected designs

using SBO

END

Acquire data

Construct kriging model

Optimize using MOEA

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

800

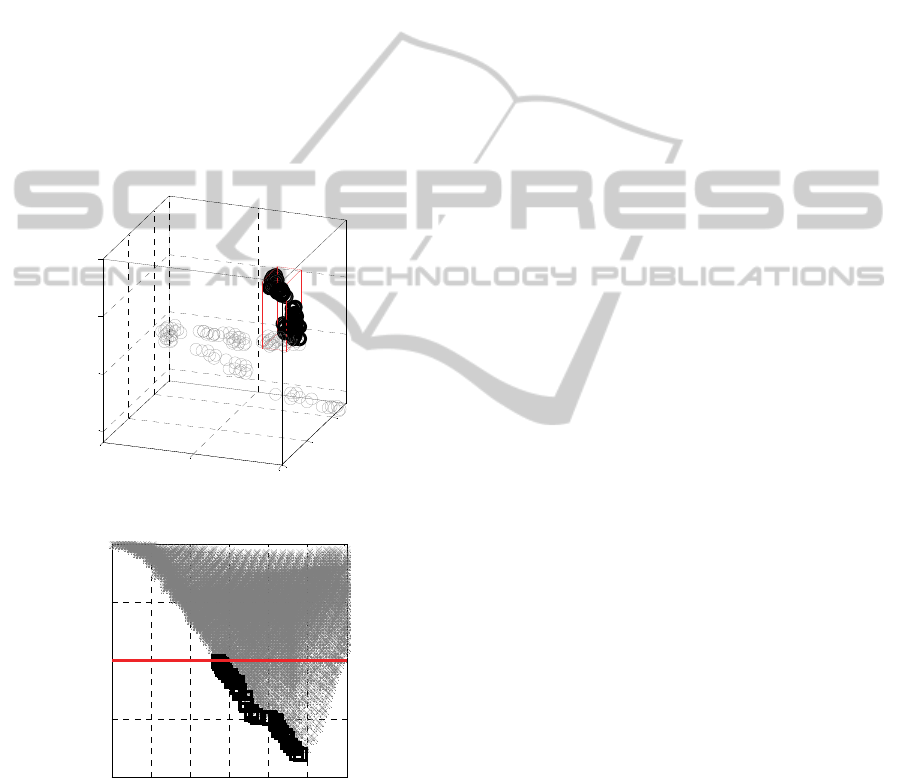
Figure 2 shows a typical example of such a

situation, here, for a UWB monopole antenna

(Bekasiewicz et al., 2014c). Nonetheless, setting up

the RSA model in such a large solution spaces is

virtually impractical. In the proposed approach,

frontiers of the solution space are reduced using

single-objective optimizations with respect to each

design goal. Consider l and u as initial lower/upper

bounds for the design variables. Let





*( )

arg min ( )

cd k cd





lxu

xRx

(2)

where k = 1, … N

obj

, is an optimal design of the low

fidelity-model R

with respect to the kth objective.

These extreme (or corner) points of the Pareto

optimal-set are denoted by x

*(k)

. Frontiers of the

reduced design space can be then defined as follows:

(a)

(b)

Figure 2: (a) Visualization of the Pareto optimal set (○) in 3-

dimensional solution space (data for UWB monopole

antenna, Bekasiewicz et al., 2014). The portion of the design

space that contains the part of the Pareto set we are interested

in (red cuboid, where F

≤ –10) is only a small fraction of the

initial space. (b) the Pareto set of interest (□) versus the entire

design space mapped to the feature space (×).

l* = min{x

*(1)

, …, x

*(Nobj)

} (3)

u* = min{x

*(1)

, …, x

*(Nobj)

} (4)

The reduced solution space is usually orders of

magnitude (volume-wise) smaller than the initial

one, which makes the generation of an accurate RSA

model possible at a low computational expense. One

should note that utilization of the proposed method

cannot ensure the existence of all Pareto optimal

solutions within refined design space; however, the

majority of them are usually accounted for.

3 CASE STUDY: PLANAR

YAGI-UDA ANTENNA

In order to demonstrate the presented design

concepts, let us consider a planar Yagi-Uda antenna

shown in Fig. 3. The antenna is designed to work on

Taconic RF-35 substrate (ε

= 3.5, tanδ = 0.0018, h =

0.762 mm). The structure is an extended version of

antenna discussed in (Qian et al., 1998) and it

comprises a driven element feed by a microstrip-to-

coplanar strip transition, three directors and a

microstrip balun. The input impedance is 50 Ω. In

the design process, the following two objectives are

considered:

 F

– minimization of VSWR (with the maximum

allowed VSWR equal to 2 for the entire

frequency range of interest, here, 5.2 GHz to 5.8

GHz), and

 F

– maximization of average gain in 5.2 GHz to

5.8 GHz frequency range.

The antenna geometry is described by 12

parameters: x = [s

]

Parameters w

= 1.7, w

= 3, w

= 0.85 and w

= 0.85

remain fixed (all dimensions in mm). The high-

fidelity model R

of the antenna (~600,000 mesh

cells, average evaluation time of 25 minutes) and its

low-fidelity counterpart R

(~110,000 mesh cells,

evaluation time of 150 seconds) are both

implemented in CST Microwave Studio (CST, 2013)

and evaluated using its transient solver. The initial

lower/upper bounds are l = [2 2 2 2 18 7 7 7 3 7 2

, and u = [10 10 10 10 30 15 15 15 12 16 6 3]

4 OPTIMIZATION RESULTS

In the first stage of the design process, the technique

described in Section 2.3 has been applied to

determine the reduced search space boundaries:

5 10 15 20 25 30 35

-20

-15

-10

-5

ComputationallyEfficientMulti-ObjectiveOptimizationofandExperimentalValidationofYagi-UdaAntenna

801

= [4.05 3.75 2.93 2 22.89 13 14.6 8 4.93 12.34 4.2

1.96]

, and u

= [7.39 9.75 8.93 10 24.22 15 14.6 15

8.93 13.01 4.2 2.62]

. Compared to the initial

bounds, a five orders of magnitude reduction

(volume-wise) has been obtained.

In the next stage, the response surface

approximation model was constructed using 1300

training samples allocated by means of Latin

Hypercube Sampling (Beachkofski and Grandhi,

2002). The generalization error of the model

estimated using cross-validation (Queipo et al.,

2005) is only 1% for VSVR and 0.1% for gain. It

should be reiterated that it is not possible to

construct such accurate RSA models in the original

design space unless significantly larger number of

training samples are utilized.

The initial Pareto optimal set has been identified

using multi-objective evolutionary algorithm applied

to the surrogate model R

. In the last stage, a set of

ten designs has been selected from the initial Pareto

set and refined using the procedure described in

Section 2.2. The results are shown in Table 1

(detailed antenna dimensions for the selected

designs) and Fig. 4 (initial and refined Pareto sets).

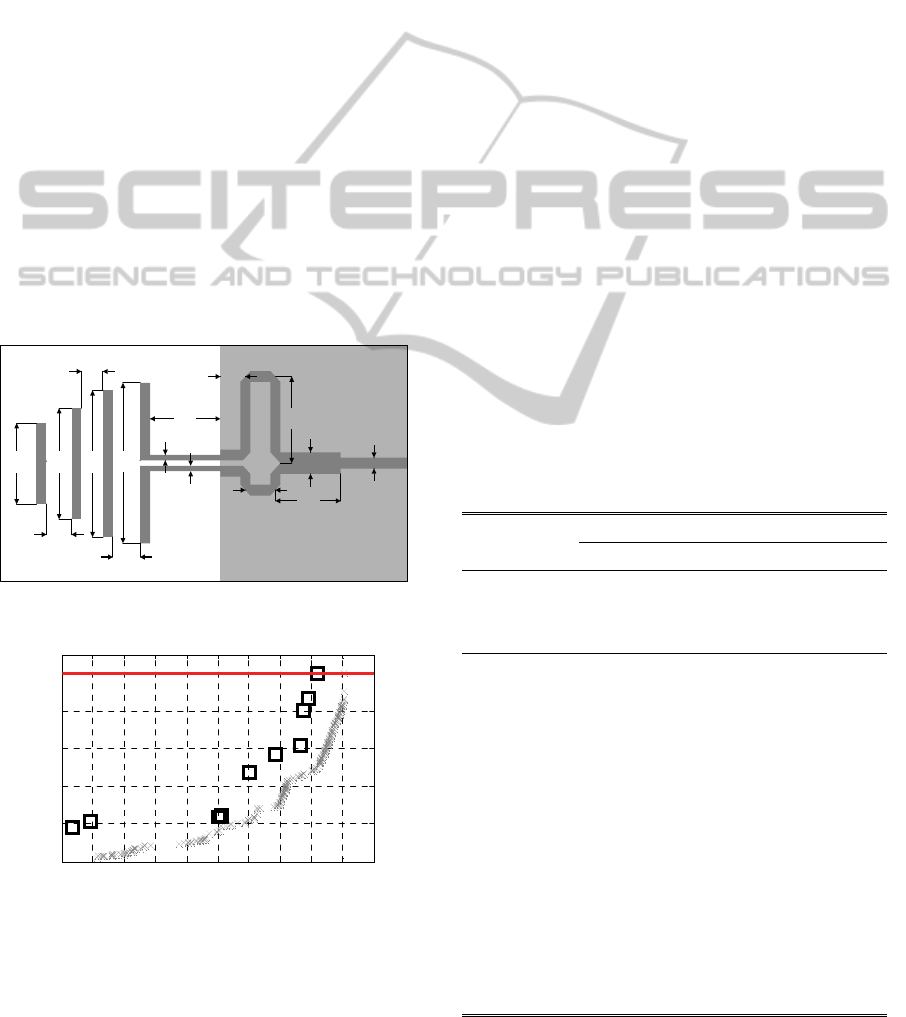
Figure 3: Layout of 12-variable planar Yagi-Uda antenna.

Figure 4: Pareto set of optimized RSA model R

(×)

obtained by the proposed multi-objective optimization

procedure and 11 refined high-fidelity designs R

(□)

obtained by (1).

It can be observed that the minimum antenna

VSVR is 1.177 (with the corresponding average gain

of 6.47 dB). The maximum average gain possible for

this antenna is 8 dB while still maintaining the

VSVR level of 2 within the entire frequency band of

interest. Figure 5 shows the frequency responses of

the antenna for a few designs selected along the

Pareto set.

It is interesting to analyse the cost of multi-

objective antenna design using the proposed

technique. In the first stage (design space reduction),

334 R

evaluations were used to execute single-

objective evaluations (220 R

and 114 R

evaluations for minimization of F

and

maximization of F

, respectively). The response

surface approximation model was constructed using

additional 1300 R

samples. Multi-objective

optimization of the RSA model is a very fast

process, the cost of which corresponds to less than

one high-fidelity model evaluation. Finally, the

refinement step requires 30 R

evaluations. The total

aggregated cost of Yagi-Uda antenna optimization is

about 194 R

simulations (~81 hours of CPU time),

which is very low compared to direct multi-objective

optimization using population-based metaheuristic,

the latter requiring at least a few thousands of high-

fidelity model evaluations (estimated using the

number of evaluations of R

model during MOEA

optimization).

Table 1: Multi-objective optimization results for planar

Yagi-Uda antenna.

Selected designs

(1)

(3)

(5)

(8)

(10)

VSVR 1.177 1.240 1.573 1.801 2.003

Average gain

[dB]

6.472 7.425 7.771 7.957 8.041

Design variables [mm]

7.38 6.19 6.03 4.87 4.30

3.79 3.82 7.57 9.46 9.75

3.08 7.24 6.94 8.10 8.44

9.41 9.61 9.75 9.98 9.92

24.03 23.96 23.00 23.03 22.96

14.65 14.95 14.97 14.92 14.99

14.60 14.60 14.60 14.60 14.60

11.52 14.81 14.78 15.00 15.00

8.08 7.36 5.49 5.44 5.11

12.36 12.39 12.40 12.35 12.34

4.20 4.20 4.20 4.20 4.20

2.24 2.59 1.98 2.01 2.35

GND

6.4 6.6 6.8 7 7.2 7.4 7.6 7.8 8 8.2 8.4

1.2

1.4

1.6

1.8

(Average Gain) [dB]

(max(VSWR) in band)

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

802

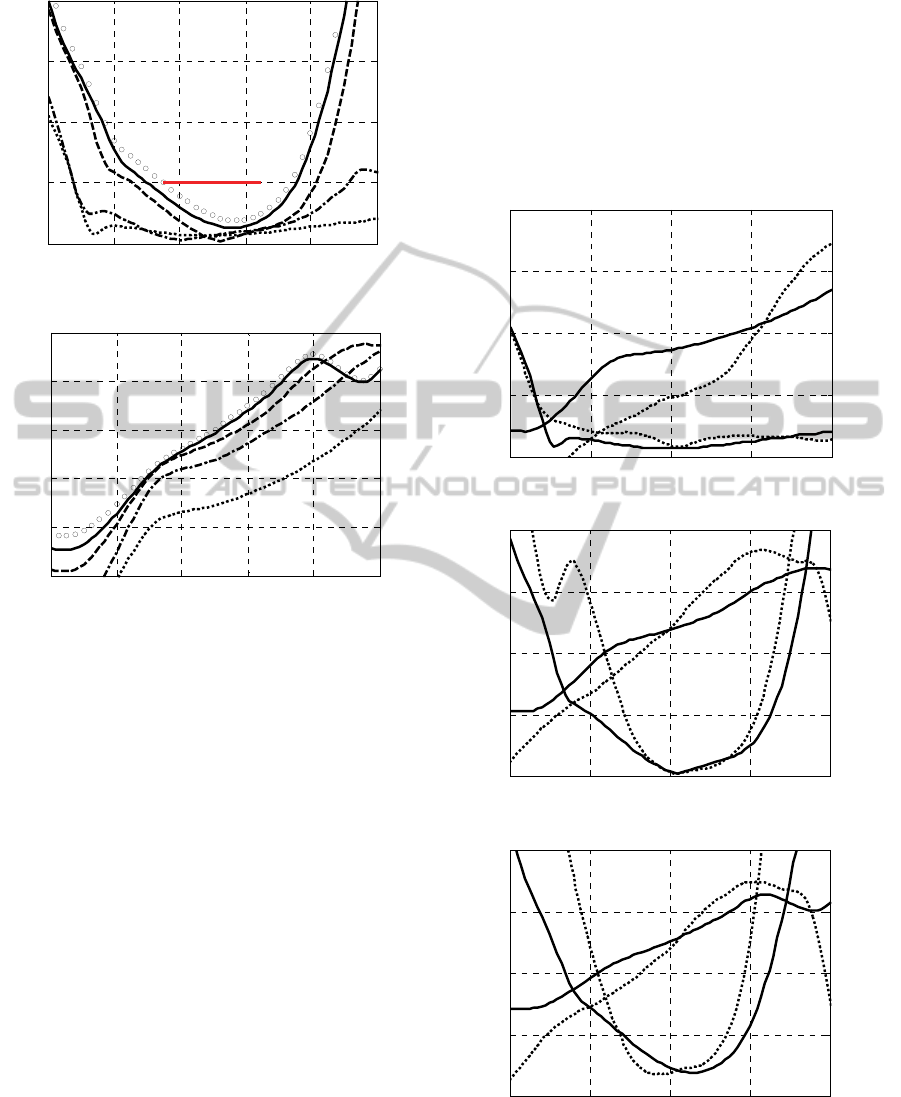
(a)

(b)

Figure 5: Frequency characteristics of the designs from

Table I: x

(1)

– (···), x

(3)

– (– · –), x

(5)

– (– – –),x

(8)

– (–––),

(10)

– (○○○).

It should be emphasized that multi-objective

optimization is essential to obtain comprehensive

information about the structure under design, here,

the considered Yagi-Uda antenna. The knowledge

about possible trade-offs between conflicting

objectives is fundamental for making design

decisions, in particular selecting the antenna

structure for a particular application. The proposed

technique allows us to gather this information at a

low computational cost and it is doable on a single-

processor machine in hours rather than weeks (the

latter typical for metaheuristic-based optimization,

see, e.g., Chamaani et al., 2011).

5 EXPERIMENTAL

VALIDATION

Selected antenna designs (x

(1)

, x

(5)

, x

(10)

– see Table

1 for dimensions) have been fabricated in order to

carry out experimental verification of the proposed

multi-objective design and optimization technique.

Both, reflection and gain have been measured using

vector network analyser. The latter has been

determined using three antenna method based on

Friis transmission equation (Balanis, 2005). A

comparison of simulation and measurement results

is shown in Fig. 6, whereas a photograph of the

fabricated circuits is shown in Fig. 7.

(a)

(b)

(c)

Figure 6: Simulation (—) and measurement (···) results of

optimized Yagi-Uda antennas in terms of voltage standing

wave ratio and gain: (a) x

(1)

; (b) x

(5)

; (c) x

(10)

4.5 4.9 5.3 5.7 6.1 6.5

VSWR

Frequen cy [GHz]

4.5 4.9 5.3 5.7 6.1 6.5

Gain [dB]

Frequen cy [GHz]

4.5 5 5.5 6 6.5

Frequency [GHz]

VSWR

Gain [dB]

4.5 5 5.5 6 6.5

Gain [dB]

4.5 5 5.5 6 6.5

Frequency [GHz]

VSWR

Gain [dB]

4.5 5 5.5 6 6.5

Gain [dB]

4.5 5 5.5 6 6.5

Frequency [GHz]

VSWR

Gain [dB]

4.5 5 5.5 6 6.5

Gain [dB]

ComputationallyEfficientMulti-ObjectiveOptimizationofandExperimentalValidationofYagi-UdaAntenna

803

Figure 7: Photograph of a fabricated antennas, from the

top: x

(1)

, x

(5)

, x

(10)

A slight difference in VSWR factor can be

observed for x

(5)

and x

(10)

antenna realizations,

which is due to the lack of connector in the EM

antenna model. Slight differences between gain

responses can also be observed. They are introduced

by impedance and polarization matching errors

during measurement procedure.

6 CONCLUSIONS

In this work, a simple yet robust and

computationally efficient technique for multi-

objective optimization of multi-parameter Yagi-Uda

antenna has been presented. Our approach exploits

variable-fidelity EM simulations and a response

surface approximation (RSA) model (here, realized

as kriging interpolation). An important step of the

process, i.e., initial reduction of the design space,

allows for constructing the RSA surrogate using a

limited number of training samples, even though the

number of designable parameters is relatively large.

The Pareto optimal-set is obtained at a cost of less

than 200 high-fidelity model evaluations, which is a

considerable speedup in comparison to direct multi-

objective optimization using population-based

metaheuristics. The selected designs have been

fabricated and measured for the sake of an additional

validation of the design procedure.

ACKNOWLEDGEMENTS

The authors thank Computer Simulation Technology

AG, Darmstadt, Germany, for making CST

Microwave Studio available. This work was

supported in part by the Icelandic Centre for Research

(RANNIS) Grant 141272051.

REFERENCES

Afshinmanesh, F., Marandi, A., Shahabadi, M. 2008.

Design of a Single-Feed Dual-Band Dual-Polarized

Printed Microstrip Antenna Using a Boolean Particle

Swarm Optimization. In IEEE Transactions on

Antennas and Propagation, 56, 1845—1852.

Balanis, C.A. 2005. Antenna theory: analysis and design.

John Wiley & Sons, 3

edition.

Bandler, J.W., Cheng, Q.S., Dakroury, S.A., Mohamed,

A.S., Bakr, M.H., Madsen, K., Søndergaard, J. 2004.

Space mapping: the state of the art. In IEEE

Transactions on Microwave Theory and Techniques,

52, 337—361.

Beachkofski, B., Grandhi, R. 2002 Improved distributed

hypercube sampling. In American Institute of

Aeronautics and Astronautics, paper AIAA 2002-

1274.

Bekasiewicz, A., Koziel, S., Leifsson, L. 2014. Low-cost

EM-simulation-driven multi-fidelity optimization of

antennas. In International Conference on

Computational Science – Procedia Computer Science,

29, 769—778.

Bekasiewicz, A., Koziel, S., Zieniutycz, W. 2014. Design

Space Reduction for Expedited Multi-Objective

Design Optimization of Antennas in Highly-

Dimensional Spaces. In Solving Computationally

Extensive Engineering Problems: Methods and

Applications.

Bekasiewicz, A., Koziel, S., Ogurtsov, S., Zieniutycz, W.

2014. Design of Microstrip Antenna Subarrays: A

Simulation-Driven Surrogate-Based Approach. In

International Conference on Microwave Radar and

Wireless Communications, 1, 177—180.

Chamaani, S., Mirtaheri, S.A., Abrishamian, M.S. 2011.

Improvement of Time and Frequency Domain

Performance of Antipodal Vivaldi Antenna Using

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

804

Multi-Objective Particle Swarm Optimization. In

IEEE Transactions on Antennas and Propagation, 59,

1738—1742.

Conn, A.R., Scheinberg, K., Vicente, L.N. 2009.

Introduction to Derivative-Free Optimization. In MPS-

SIAM Series on Optimization, MPS-SIAM.

CST Microwave Studio 2013. Computer Simulation

Technology AG, Bad Nauheimer Str. 19, D-64289

Darmstadt, Germany.

Deb., K. 2001. Multi-Objective Optimization Using

Evolutionary Algorithms. John Wiley & Sons. New

York.

Ding, D., Wang, G. 2013. Modified Multiobjective

Evolutionary Algorithm Based on Decomposition for

Antenna Design. In IEEE Transactions on Antennas

and Propagation, 61, 5301—5307.

Jin, N. Rahmat-Samii, Y., 2007. Advances in Particle

Swarm Optimization for Antenna Designs: Real-

Number, Binary, Single-Objective and Multiobjective

Implementations. In IEEE Transactions on Antennas

and Propagation, 55, 556—567.

Jin, N., Rahmat-Samii, Y. 2010. Hybrid Real-Binary

Particle Swarm Optimization (HPSO) in Engineering

Electromagnetics. In IEEE Transactions on Antennas

and Propagation, 58, 3786—3794.

Junwei L., Ireland, D., Lewis, A. 2009 Multi-Objective

Optimization in High Frequency Electromagnetics—

An Effective Technique for Smart Mobile Terminal

Antenna (SMTA) Design. In IEEE Transactions on

Magnetics, 45, 1072—1075.

Kolundzija, B.M., Olcan, D.I. 2006. Multiminima

heuristic methods for antenna optimization. In IEEE

Transactions on Antennas and Propagation, 54,

1405—1415.

Koulouridis, S., Psychoudakis, D., Volakis, J. 2007.

Multiobjective Optimal Antenna Design Based on

Volumetric Material Optimization. In IEEE

Transactions on Antennas and Propagation, 55, 594—

603.

Koziel, S., Cheng, Q.S., Bandler, J.W. 2008. Space

mapping. In IEEE Microwave Magazine, 9, 105—122.

Koziel, S., Bandler, J.W. 2012. Accurate modeling of

microwave devices using kriging-corrected space

mapping surrogates. In International Journal of

Numerical Modelling: Electronic Networks, Devices

and Fields, 25, 1—14.

Koziel, S., Ogurtsov, S. 2013. Multi-Objective Design of

Antennas Using Variable-Fidelity Simulations and

Surrogate Models. In IEEE Transactions on Antennas

and Propagation, 61, 5931—5939.

Koziel, S., Leifsson, L., Ogurtsov, S. 2013. Reliable EM-

driven microwave design optimization using manifold

mapping and adjoint sensitivity. In Microwave and

Optical Technology Letters, 55, 809—813.

Koziel, S., Ogurtsov, S., Couckuyt, I., and Dhaene, T.

2013. Variable-Fidelity Elec-tromagnetic Simulations

and Co-Kriging for AccurateModeling of Antennas. In

IEEE Transactions on Antennas and Propagation, 61,

1301—1308.

Koziel, S., Bekasiewicz, A., Zieniutycz, W. 2014 Expedite

EM-Driven Multi-Objective Antenna Design in

Highly-Dimensional Parameter Spaces. In IEEE

Antennas and Wireless Propagation Letters, 13, 631—

634.

Kuwahara, Y. 2005. Multiobjective optimization design of

Yagi-Uda antenna. In IEEE Transactions on Antennas

and Propagation, 53, 1984—1992.

Nocedal, J., Wright, S. 2006. Numerical optimization,

Springer, 2

edition.

Lophaven, S.N., Nielsen, H.B., Søndergaard, J. 2002

DACE: a Matlab kriging toolbox, Technical

University of Denmark.

Qian, Y., Deal, W.R., Kaneda, N., Itoh, T. 1998.

Microstrip-fed quasi-Yagi antenna with broadband

characteristics. In Electronics Letters, 34, 2194—

2196.

Queipo, N.V., Haftka, R.T., Shyy, W., Goel, T.,

Vaidynathan, R., Tucker, P.K. 2005 Surrogate-based

analysis and optimization. In Progress in Aerospace

Sciences, 41, 1—28.

Sharaqa, A., Dib, N. 2013. Position-only side lobe

reduction of a uniformly excited elliptical antenna

array using evolutionary algorithms. In IET

Microwaves, Antennas & Propagation, 7, 452—457.

Simpson, T.W., Peplinski, J., Koch, P.N., Allen, J.K.

2001. Metamodels for computer-based engineering

design: survey and recommendations. In Engineering

with Computers, 17, 129—150.

Talbi, E.-G. 2009. Metaheuristics – From Design to

Implementation. John Wiley & Sons.

Yang, X.-S., Ng, K.-T. Yeung, S.H., Man, K.F. 2008.

Jumping Genes Multiobjective Optimization Scheme

for Planar Monopole Ultrawideband Antenna. In IEEE

Transactions on Antennas and Propagation, 56,

3659—3666.

ComputationallyEfficientMulti-ObjectiveOptimizationofandExperimentalValidationofYagi-UdaAntenna

805