A Comparison of Two Fitting Functions for Sacadic

Pulse Component Mathematical Modelling

Rodolfo Garc´ıa-Berm´udez

, Camilo Vel´azquez

, Fernando Rojas

Roberto Becerra

, Michel Vel´azquez

, Liliana L´opez

and Luis Vel´azquez

University of Holgu´ın, Biomedical Data Processing Research Group (GPDB),

80100, Holgu´ın, Cuba

University of Granada, Department of Computer Architecture and Technology, ETS Ing.

Inform´atica y de Telecomunicaci´on, 18071 Granada, Spain

Centre for the Research and Rehabilitation of Hereditary Ataxias “Carlos J. Finlay”,

80100, Holgu´ın, Cuba

Abstract. An accepted model for the saccade signal of ocular motor neurons

comprises two components in the form of a pulse and a step. In this contribution,

an assessment of two ﬁtting functions for the saccadic pulse component is made,

in order to obtain a reduced set of descriptors that could be used for the early

diagnosis of ataxia. Results show that both models have achieved to describe the

waveform of the saccadic pulse signal, revealing higher performance of Gauss

series over the gamma function.

1 Introduction

Ocular movements are affected by inherited spinocerebellar ataxias [3, 1,2,4], spe-

cially the behavior of saccadic system is modiﬁed, patients show increased latencies

to respond to visual stimulation with slower saccades among other impairments of this

system [5].

An accepted model for saccades generation involves two components, oculomotor

plant is driven by a pulse-step to produce a saccade [6]. Several works have been using

independent component analysis to isolates pulse and step components in saccadic and

vergence ocular movements [7, 9, 8]. Based in these results in a precedent work we

have applied independent component analysis to noisy electro-oculographic records of

patients, of ataxia SCA2, characterized by severely deformed saccades and the pulse

and step components were obtained [10]. In order to evaluate the pulse component

several of its parameters has been used, as duration, amplitude, the time to reach a

determined percent of the ﬁnal value (not including the latent period) [12,9,11] among

others. An important limitation common in the estimation of these variables is the need

to use thresholds to identify onset and offset of the pulse.

In the present work an evaluation of two ﬁtting functions for the pulse component is

made in order to obtain a reduced set of descriptors to be used for classiﬁcation purposes

of ataxia patients and presymptomatics with respect to healthy subjects.

García-Bermúdez R., Velázquez C., Rojas F., Becerra R., Velazquez M., López L. and Velázquez L..

A Comparison of Two Fitting Functions for Sacadic Pulse Component Mathematical Modelling.

DOI: 10.5220/0005136800880094

In Proceedings of the International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing (ANNIIP-2014), pages 88-94

ISBN: 978-989-758-041-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 Materials and Methods

All the experiments and material were handled by the medical staff of the Centre for the

Research and Rehabilitation of Hereditary Ataxias (CIRAH) at Holgu´ın (Cuba). A two-

channel electronystagmograph (Otoscreen, Jaeger-Toennies, Hochberg, Germany) was

used to record saccadic ocular movements. Subjects were seated on chair with special

ﬁxation accessory to avoid head movements, and asked to follow a divergence stimuli

conformed by a white circular target in a blank screen. The target appeared suddenly

at each side of the screen at random time slots between 1s and 3 s, the distance from

subject to screen was adjusted to obtain an angular distance of 30 degrees.

A group of 19 records of patients of ataxia was collected and the 29 records of

presymptomatic individuals with genetic evidence of the disease but without detected

symptoms and a third group of 23 records of healthy subjects. Saccades were identiﬁed

using an automated algorithm based in a velocity threshold of 10 degrees per second,

after this step a manual process of visual inspection was made to eliminate saccades

considered anticipatory (latencies lower than 100 ms) or with artifacts like blinkings,

excessive noise, muscle or extra ocular movements in the close time before onset, or

in the next ﬁxation. In the next step the mean of amplitude, duration and latency were

calculated and saccades with deviations higher than 20% were excluded, in similar way

as it is described in [10].

2.1 Obtaining Pulse and Step Components

Independent component analysis (ICA) is a well knownmethod for estimation of under-

lying components in mixtures of non gaussian and statistically independent variables.

The aim of ICA is to ﬁnd the linear matrix W which mixes the x independent compo-

nents to produce a set of y observed signals, as it is shown in the equation 1:

y = W × x. (1)

To apply ICA as observations are considered an ensemble of saccades after the

process of identiﬁcation and exclusion of non valid saccades, where each row is a vector

containing a saccade:

S =



. . . s

. . . .

. . . s



(2)

An Infomax ICA [13] algorithm implemented in matlab [14] was used accordingly

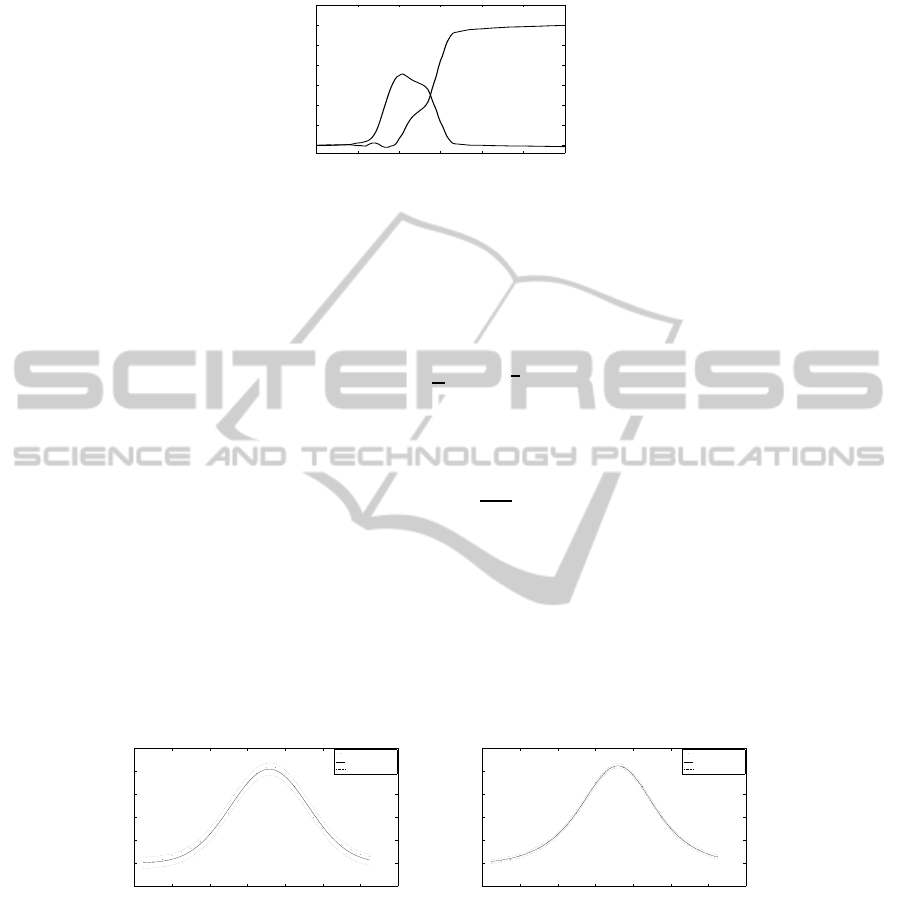
to the procedure described in [10]. Figure 1 shows the pulse and step obtained for a

patient of ataxia.

2.2 Pulse Component Fitting

The ﬁtting of step component using a sigmoid function was treated in a precedent work

[10], four coefﬁcients were estimated and used in conjunction with the value and latency

0 100 200 300 400 500 600

Time (ms)

Component value (degrees)

Fig.1. Pulse and step components.

of the maximum of the pulse component for classiﬁcation purposes. The best results of

experimental tests with several functions to ﬁt the pulse components were achieved

with the gamma function, previously used to model the velocity behavior of saccadic

movements [15], and gaussian series with diferent numbers of terms. The equation of

the gamma function is the following:

f(x) = a

c−1

−

(3)

Where a, b, c and d are the coeﬁcients to be adjusted.

While the gaussian series is expressed by:

f(x) =

i=1



−



x−b





(4)

Where the coefﬁcients for each term are a

, b

, c

The function ﬁtting procedure was made by means of the ﬁt function implemented

in matlab. Prior to the ﬁtting process the active pulse segment was identiﬁed, in order to

consider only this part of the signal. The onset and offset points were marked examining

the ﬁrst derivative of the signal at left (onset point) and right (offset point) sides of the

central maximum value, until a value of 0 was found. Figure 2 shows a segmented pulse

ﬁtted by gamma function (left) and using a two terms Gauss series (right).

0 20 40 60 80 100 120 140

−1

Time (ms)

Component value (degrees)

data

fitted curve

prediction bounds

0 20 40 60 80 100 120 140

−1

Time (ms)

Component value (degrees)

data

fitted curve

prediction bounds

Fig.2. Pulse component ﬁtted using a gamma (left) and Gauss1 (right) function.

3 Results

The ﬁtting was applied to all the records, using gamma function and Gauss series from

one up to ﬁve terms. A visual inspection of the graphics for every record and ﬁtting

function was done to rank the results, when no differences were seen among several

Table 1. Ranking of ﬁtting functions.

Fitting functions 1 2 3 4 5 6

Gamma 0.97% 28.64% 49.51% 11.65% 1.94% 0.49%

Gauss1 3.88% 38.83% 32.04% 19.9% 5.34% 0%

Gauss2 62.14% 28.16% 6.8% 2.43 % 0% 0%

Gauss3 80.01% 7.28% 2.43% 0% 0% 0%

Gauss4 82.04% 1.46% 0% 0% 0% 0%

Gauss5 73.79% 1.46% 0.49% 0% 0% 0%

functions, same rank was assigned to them for this record. This is summarized in Table

Results from Table 1 reveal gamma function worse performance when compared

with the Gauss series. Best results are achievedby Gauss2 and highers. Table 2 shows an

analysis of the success in ﬁtting of each function, gamma function is below Gausss1 and

Gauss2, from Gauss3 this indicator deteriorates. An overall evaluation of both tables

points to Gauss2 as the best, with a very low percent of failed ﬁttings and ranked ﬁrst

or second about 80% of the cases, while gamma is in general sense worst than Gauss

series.

Table 2. Failures of ﬁtting functions.

Fitting functions Number of failed ﬁttings Percent of failed ﬁttings

Gamma 14 6.8%

Gauss1 0 0%

Gauss2 1 0.49%

Gauss3 21 10.19%

Gauss4 34 16.5%

Gauss5 50 24.27%

Gauss series of higher order has the inconvenience of the increased number of coef-

ﬁcients (three per term), otherwise gamma and Gauss1 with only three coefﬁcients. An

analysis of the correlation coefﬁcient of Pearson (Figure 3 left) and root medium square

error (Figure 3 right) as metrics for the goodness of th ﬁt accounts for gamma as the

worst function, while the Gauss series has sustained improvements with the increment

in the number of terms.

0.97

0.975

0.98

0.985

0.99

0.995

Gamma

Gauss1

Gauss2

Gauss3

Gauss4

Gauss5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

Gamma

Gauss1

Gauss2

Gauss3

Gauss4

Gauss5

Fig.3. Pearson’s correlation coefﬁcients (left) and RMSE (right) results of ﬁtting functions.

3.1 Analysis of Fitting Coefﬁcients

The ﬁtting procedure for gamma functions failed for 5 records of patients of ataxia (14

well ﬁtted), six presymtomatics (23 well ﬁtted) and 3 healthy subjects (20 well ﬁtted),

Gauss1 showed no failures and Gauss2 failed for one patient (not coincident with those

ones failed by gamma). Given the limited quantity of available records it was decided

to compare gamma and Gauss1 ﬁtting functions. A random selection of the resultant

records of presymtomatics and healthy subjects was made to obtain fourteen records

in each class of subjects for this preliminary analysis of the relationships among ﬁtting

coefﬁcients and classes of subjects.

Figure 4 represents the coefﬁcients of gamma function versus the category of the

subjects, it can be seen overlapping among categories for the three variables. Otherwise,

in Figure 5 is possible to observe better deﬁned clusters in the categories of healthy sub-

jects and patients of ataxia for coefﬁcients b and c, while presymptomatics are located

between these categories, probably depending on their progression in the disease. It

must be noticed the bigger separation between means and similar dispersion observed

for coefﬁcient b, this is conﬁrmed by the values of the mean and standard deviation of

each coefﬁcient (Table 3).

Healthy Presymptomatics Patients

Fig.4. Coefﬁcients a (left), b (center) and c (right) of gamma ﬁtting function vs category.

Healthy Presymptomatics Patients

Fig.5. Coefﬁcients a (left), b (center) and c (right) of Gauss1 ﬁtting function vs category.

Table 3. Means and standard deviations of coefﬁcients of Gauss1 ﬁtting function.

Category Coefﬁcients

a b c

mean std mean std mean std

Healthy 14,1 3,1 22,8 6,0 11,8 4,2

Presimptomatics 14,2 2,5 30,6 8,3 18,3 6,3

Patient 15,8 2,4 57,9 10,2 36,4 9,1

4 Discussion

Simple visual inspection reveals higher performance of Gauss series over gamma func-

tion. Regardless of the number of terms, Gauss series are better valued in terms of the

ﬁtting performance. Additionally Gauss1 and Gauss2 have very low failing rates, as

compared to gamma function or Gauss series of higher orders, an appropriate selection

of initial is very difﬁcult when the number of coefﬁcients increases.

This superiority is consistent with the numerical results of two of the most used

parameters to assess the goodness of ﬁt: the Pearson’s correlation coefﬁcient and the

RMSE value. For both parameters gamma function has a poorer performance with

respect to Gauss series. Although the Pearson’s correlation coefﬁcient is above 0.95,

which can be considered an expression of a good ﬁtness for all the functions, there exist

an considerable difference of gamma and one term Gauss series with respect to Gauss

of 2 terms or higher. The lack of an enough number of records inhibits to do a consistent

analysis of the behaviour of the ﬁtting coefﬁcients for the studied functions, this is more

evident for Gauss series with a higher number of terms. However a comparison with a

limited set of register for Gauss1 and gamma could be made, in order to evaluate the

clustering ability of the coefﬁcients taken separately. For gamma function only b seems

to be able to identify between healthy subjects and patients of ataxia, presymptomatics

are located in a middle overlap zone with respect to the two extreme groups.

Similar results were found for coefﬁcients b and c of the Gauss1 series. The vi-

sual inspection and the analysis of mean and standard deviation were in coincidence to

identify coefﬁcient b of Gauss1 as the best to classify subjects. No data was available

concerning other signiﬁcant medical variables to correlates the condition of presymp-

tomatics with the value of b, but it is reasonably to believe that b could be a signiﬁcant

marker of the progression of the disease, even before other symptoms are to be present.

These results were not improved when more than one coefﬁcient was used for cluster-

ing, in fact visual inspection revealed the presence of linear correlation between b and

c for Gauss1.

5 Conclusions

In this contribution two ﬁtting function has been evaluated for modelling of saccadic

pulse component obtained by the application of ICA to electro-oculographic records,

gamma function and Gauss series. Both models have achieved to describe the wave-

form of the signal in its active area, conﬁrmed by the analytical results. Accordingly to

the trade off between successful ﬁttings and quality Gauss2 could be considered as the

best choice, although the presence of two terms implies the need of 6 coefﬁcients. On

the other hand the use of only one of the coefﬁcients of Gauss1 proved to be a good

feature to classify subjects in the extreme categories of patients and healthy subjects,

and as a probable indicator of the condition of presymptomatics, however these results

must be considered preliminaries and further research is necessary to explain relation-

ships between the condition of the subjects and the coefﬁcients derived from modelling.

References

1. Fahey M. C., Cremer P. D., Aw S. T., Millist L., Todd M. J., White O. B., et al. Vestibular,

saccadic and ﬁxation abnormalities in genetically conﬁrmed Friedreich ataxia. Brain. 1 de

abril de 2008;131(4):1035-45.

2. Hutton J. T., Albrecht J. W., Kuskowski M, Schut L. J. Abnormal ocular motor function

predicts clinical diagnosis of familial ataxia. Neurology. 1987;37(4):698-701.

3. B¨urk K., Fetter M., Abele M., Laccone F., Brice A., Dichgans J., et al. Autosomal dominant

cerebellar ataxia type I: oculomotor abnormalities in families with SCA1, SCA2, and SCA3.

J Neurol. 1999;246(9):789-97.

4. Moschner C., Perlman S., Baloh R. W. Comparison of oculomotor ﬁndings in the progressive

ataxia syndromes. Brain. 1994;117(1):15-25.

5. Vel´azquez P´erez L., S´anchez Cruz G., Canales Ochoa N., Rodr´ıguez Labrada R., Rodr´ıguez

D´ıaz J., Almaguer Mederos L., et al. Electrophysiological features in patients and presymp-

tomatic relatives with spinocerebellar ataxia type 2. J Neurol Sci. 15 de diciembre de

2007;263(1-2):158-64.

6. Robinson D. A. Models of the saccadic eye movement control system. Biol Cybern. 1 de

junio de 1973;14(2):71-83.

7. Chen Y-F., Chen T., Semmlow J. L. Decomposition of Control Signals for Saccade and

Vergence Eye Movements Using Independent Component Analysis. J Med Biol Eng.

2004;24(1):23-8.

8. Lin H-H., Chen Y-F, Chen T., Lee Y-Y. Decomposition of saccadic pulse and step com-

ponents by independent component analysis. Proceedings of the International Confer-

ence on Mathematics and Engineering Techniques in Medicine and Biological Sciences,

METMBS’04 [Internet]. 2004 [citado 3 de diciembre de 2008]. p. 124-8.

9. Chen Y-F., Lee Y-Y., Huang M-W., Du Y-C., Chen T. Analysis of decomposed saccadic

pulses and steps by independent component analysis for patients with brain stem lesions.

Proceedings of the 2005 International Conference on Mathematics and Engineering Tech-

niques in Medicine and Biological Sciences, METMBS’05 [Internet]. 2005.

10. Rojas F., Garc´ıa R. V., Gonz´alez J., Vel´azquez L., Becerra R., Valenzuela O., et al. Identiﬁ-

cation of saccadic components in spinocerebellar ataxia applying an independent component

analysis algorithm. Neurocomputing. 9 de diciembre de 2013;121:53-63.

11. Semmlow J. L., Yuan W. Adaptive Modiﬁcation of Disparity Vergence Components:

An Independent Component Analysis Study. Invest Ophthalmol Vis Sci. 1 de julio de

2002;43(7):2189-95.

12. Alvarez T. L., Daftari A., Semmlow J. L. Independent Component Analysis of Divergence

Eye Movements. Neural Engineering, 2005 Conference Proceedings 2nd International IEEE

EMBS Conference on. 2005. p. 608-11.

13. Bell A. J, Sejnowski T. J. An information-maximization approach to blind separation and

blind deconvolution. NEURAL Comput. 1995;7:1129-59.

14. Kolenda T. ICA Infomax Matlab implementation. 2003.

15. Van Opstal A. J., Van Gisbergen J. A. M. Skewness of saccadic velocity proﬁles: A unifying

parameter for normal and slow saccades. Vision Res. 1987;27(5):731-45.