
Heuristic Crossover Operator for Evolutionary Induced Decision
Trees
Sašo Karakatič and Vili Podgorelec
Institute of Informatics FERI, University of Maribor, Smetanova 17, Maribor, Slovenia
Keywords: Genetic Algorithm, Decision Tree, Crossover.
Abstract: In this paper we propose an innovative and improved variation of genetic operator crossover for the
classification decision tree models. Our improved crossover operator uses heuristic to choose the tree node
that is exchanged to construct the children solutions. The algorithm selects a single node based on the
classification accuracy and the usage of that particular node. We evaluate this method by comparing it with
the results of the standard crossover method where nodes for exchange are chosen at random.
1 INTRODUCTION
The decision tree classification method is one of the
classifiers used in the machine learning field that is
notorious for its ease of interpretation by human
users and the ability to generalize the problem
solutions (Cantu-Paz & Kamath 2003). Many
methods for the construction of decision trees were
proposed in the past, but our paper is focused on the
evolutionary method of genetic programming.
Genetic programming is a variation of the genetic
algorithm where individuals in the generation are
presented with a tree structure. Each individual
presents one solution and the process of evolution
consists of several genetic operators which create
new individuals (crossover) or try to modify the
existing ones (mutation) (Koza 1992). Our paper
focuses on the crossover operator which is a method
that generates new individuals from the parent trees
in such a way, that some characteristics from both
parents are represented in the child tree – therefore
mimicking the natural process of mating, where
DNA of humans is constructed from the genetic
material from both parents.
Crossover is heavily dependent on the type of
representation used for individuals. Due to the
standard representation of decision trees being done
with a tree structure instead of an array, our focus
was on the crossover for tree genotype – genetic
programming. The crossovers on the tree are done
by exchanging the subtrees from one individual to
another, with the method of choosing these subtrees
being the main question. We propose an innovative
crossover method that tries to eliminate the weak
parts of the tree individual, based on the partial
accuracy of the subtrees and usage of that subtree.
Rest of the paper is organized as follows. We
start with the background overview of existing
research done on the crossover operators of the
decision tree models and other similar tree based
problems. We continue with the description of the
proposed improvement in the crossover operator,
where we present the idea of the innovative
crossover method. Following that, the experiment on
the standard benchmark datasets, to evaluate the
quality of our proposed improvement is presented.
The results are backed up by the statistical methods
and are supplemented with the interpretation of the
results and the discussion. In the conclusion we
summarize the paper and present the final verdict.
Possibilities for further research are also discussed.
2 RELATED WORK
Koza (Koza 1992) describes the random subtree
exchange crossover as a blind operator, due to no
context being included in the crossover location
choosing. He also introduced constrained crossover
that exchanges only two matching subtrees (Koza &
Noyes 1994). The positive effect of this is the
maintenance of the context, which allows the
subtress to evolve faster to its optimal form.
However, this has its own limitations. Namely, there
is no new genetic material entering the subtrees
which eventually leads to the local optimum.
289
Karakati
ˇ
c S. and Podgorelec V..
Heuristic Crossover Operator for Evolutionary Induced Decision Trees.
DOI: 10.5220/0005137102890293
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 289-293
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
D'haeseleer takes a different approach, where he
assigns a location to each node. He tries to extend
the initial context preserving crossover from Koza
by limiting the crossover so that only subtrees on
same location can be exchanged with its strong
context preserving crossover. As he states himself,
the greatest weakness of this crossover is the
resulting limited diversity, so he expands it with the
weak context preserving crossover where the nodes
exchanged have to have the same parent
(D’haeseleer 1994). The main disadvantage of this
type of location based crossover is that most of the
times the nodes on the same location are not in the
same context.
Iba and Garis (Iba & de Garis 1996) used a
heuristic search for subtrees, where the evaluation of
each node was calculated with the mean square error
value. By this criterion, the worst subtrees are
replaced with the best subtrees. This method is
similar to the one proposed in the paper. However,
the search for the worst subtrees can select nodes in
high depth levels, thus constructing large trees
which was never evaluated on classification
problem. In addition to that, we believe that
substitution for best subtrees eventually leads to less
diversified population of solution meaning that this
kind of method has a potential to get stuck in local
optimum early on in the evolution process.
One very similar method to ours was made by
Hengpraprohm and Chongstitvatana where they
exchanged the worst subtrees with the best ones.
They evaluated the subtrees, followed by the
pruning and comparison of the fitness pre and post
(Hengpraprohm & Chongstitvatana 2001). Same
problems may arise here, as stated previously,
replacing the worst subtrees with the best ones can
prematurely result in local optima.
Another context aware crossover was done by
Majeed and Ryan in (Majeed & Ryan 2006a) and
(Majeed & Ryan 2006b), where they make multiple
children from two parent trees and select only one of
them as the real successor that advances to the next
generation. The crossover point in the second parent
is chosen at random, while in the first parent every
legal point is used. Surveys of evolutionary
algorithms for decision trees by Barros et. al.
(Barros et al. 2012) and Espejo at. al. (Espejo et al.
2010) do not mention any other heuristic crossover
operators.
Expansion of good building block ideas came
from Zhang (Zhang et al. 2007) with his looseness
controlled operator, where he used local hill
climbing search to construct and evaluate subtrees.
He introduces the evaluation function called “sticky”
that evaluates how good do particular nodes perform
together in parent-child relationship and perform
crossover based on the stickiness values.
3 CROSSOVER IMPROVEMENT
Genetic operator crossover is one of the most
impacting operators on the final solution of the
whole process. Process of mating begins with two
parent individuals that are selected (with the
selection operator) for the creation of the child
individual. The standard procedure is to select a
random subtree in the first parent tree and exchange
it for a random subtree from the second parent tree;
the resulting tree is considered as the child
individual. Our goal was to improve this process
with heuristics in hopes of improving the results.
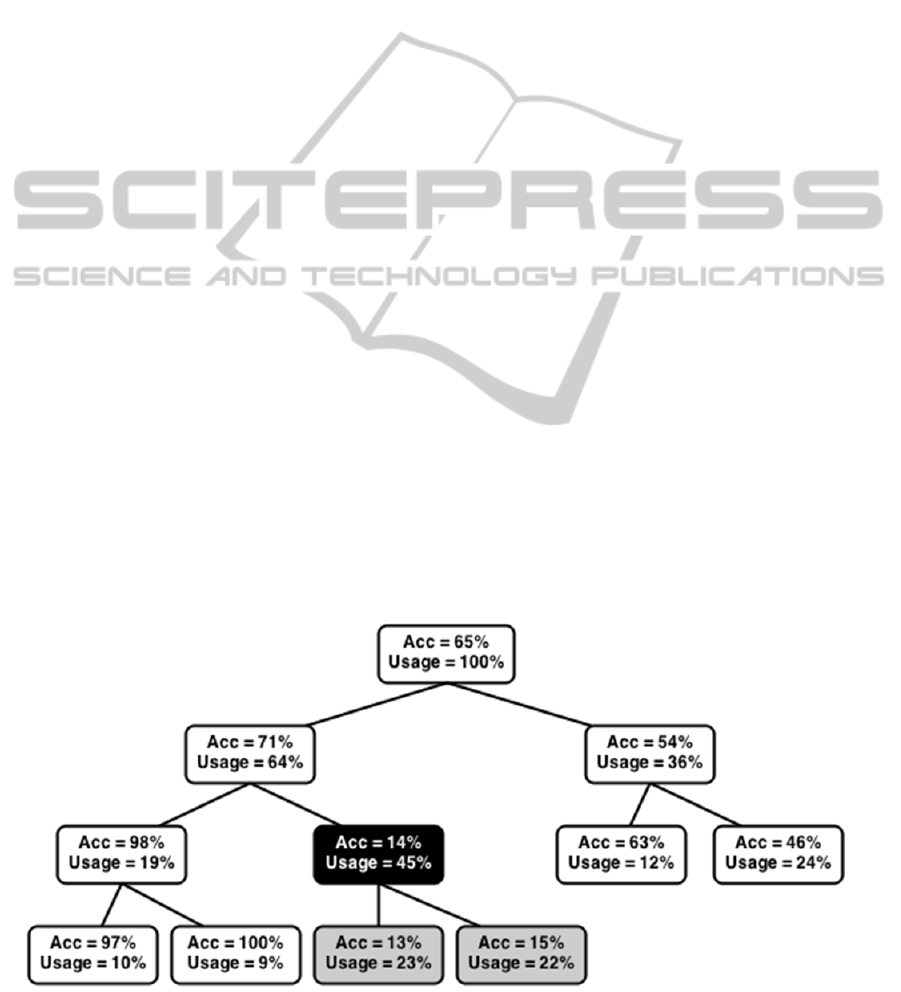
Figure 1: Evaluation of nodes in the whole tree.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
290

The nature of the decision tree is such, that we can
calculate the basic performance metrics of each
individual subtree, which is based on the instances
that were processed by that particular subtree. Our
hypothesis was that we can select the worst
performing subtree from the first parent and replace
it, so that the worst part of the tree will always be
selected for the crossover and eliminated. This will
produce the solutions with at least an equal and
hopefully even better quality based on the
classification metrics.
For the evaluation of subtrees we initially used
the overall classification accuracy of the subtree on
its instances. The results showed that this produced
somewhat better results based on the mean accuracy
of the 100 experiments, but the results were not
statistically significant. This crossover chose the
nodes with worst accuracy, which were terminal in
most instances and thus failed to make an impact by
ignoring the nodes that were used the most but were
in the higher levels of the tree. Mistakes made by the
nodes in the tree on the lower levels impact the
results much more that the nodes on the higher
levels, so a change which would force the algorithm
to choose more nodes on lower levels of decision
tree was necessary.
e = usage + error rate (1)
Based on this experience we introduced another
metric to the evaluation of the subtrees – the usage
of the root nodes on the subtrees. We reasoned that
this process should replace the subtrees with the
worst accuracy while at the same time giving more
emphasis on more used subtrees (near the root of the
tree) and essentially ignoring the nodes near the end
of the tree which are the unfortunate consequences
of randomness and processes just a few
classification instances. Combined evaluation of
nodes is calculated as the sum of the error rate (1 -
accuracy) and the usage of the node as is show in the
equation 1. Usage of the nodes is a percentage of
classification instances processed in the node during
the training phase of the genetic algorithm. This
process ignores the root node. The evaluation of the
nodes in the tree is shown in the Figure 1, where
node with the black background is the node with the
highest crossover evaluation and is chosen for the
exchange with the random subtree with the second
parent.
4 EXPERIMENT
Our genetic algorithm with proposed crossover was
Table 1: Comparison of crossovers on several datasets by overall classification accuracy.
Dataset Instances Avg standard
cx
Avg
improved cx
p Max
standard
Max
improved
autos
205 .4705
.5044 < .001
.62
.67
glass
214 .5744
.5814
.136 .73
.77
diabetes
768 .6382
.6444
.789 .70 .70
iris
150 .9447
.9480
.629 1.00 1.00
primary-tumor
339 .2601
.2741 .007
.38 .38
sonar
208 .6067
.6740 < .001
.80 .80
Table 2: Comparison of crossovers on several datasets by average Fscore.
Dataset No. of
classes
Avg standard
cx
Avg improved
cx
p Max
standard
Max
improved
autos
7 .2069
.2460 < .001
.35
.41
glass
7 .2623
.2913 < .001
.43
.50
diabetes
2 .4899
.5121 .015
.62 .62
iris
3 .9443
.9478
.597 1.00 1.00
primary-tumor
22 .0321
.0419 < .001
.08
.09
sonar
2 .5501
.6510 < .001
.79 .79
HeuristicCrossoverOperatorforEvolutionaryInducedDecisionTrees
291
implemented and tested on six standard
classification benchmark datasets. Characteristics of
the used dataset and the results of the experiments
are shown in the Table 1 and Table 2. Algorithm ran
10 times on 10 folds on each dataset (100 times in
total) in order to produce reliable results and
minimize the chance of randomness. Accuracies in
the Table 1 are means of accuracies on all 100 runs.
In addition to mean of all accuracies, we calculated
the average Fscore of all classes on the dataset for
each run and included the mean of those in the Table
2, for comparison. Independent samples Mann-
Whitney U test was conducted to ensure the validity
of the results. We added the p-values for each test.
Both, the results that are statically significant (p <
0.05) and the instances where our improved
algorithm achieved better best resulting
classification model are bolded. Crossovers are
labelled as CX.
Basic genetic algorithm settings were the same
for all of the datasets and were set as follows:
evolution process ran for 2000 generations, with
100% chance of crossover and 10% chance of basic
random mutation. Each generation consisted of 150
individual solution decision trees, where the best
individual automatically advanced to next generation
(one elite individual). Selection operator was chosen
to be binary tournament, and the fitness evaluation
method was based on the accuracy of the
individuals.
Table 1 and Table 2 show, that our proposed
crossover operator not only matched, but improved
the classification results on both metrics, the
accuracy and the average Fscore, on used datasets.
In datasets glass (p = 0.136), diabetes (p = 0.789)
and iris (p = 0.597) the difference was not as
dramatic as in other datasets, but average accuracy
achieved is still better. Based on these results we can
conclude that the proposed improvements to the
crossover methods made significant improvements,
which is unlikely due to chance, on chosen datasets.
Out of six datasets, our algorithm matched 4 of them
in the best resulting model and was better in other 2
datasets in the overall accuracy. In the Table 2 and
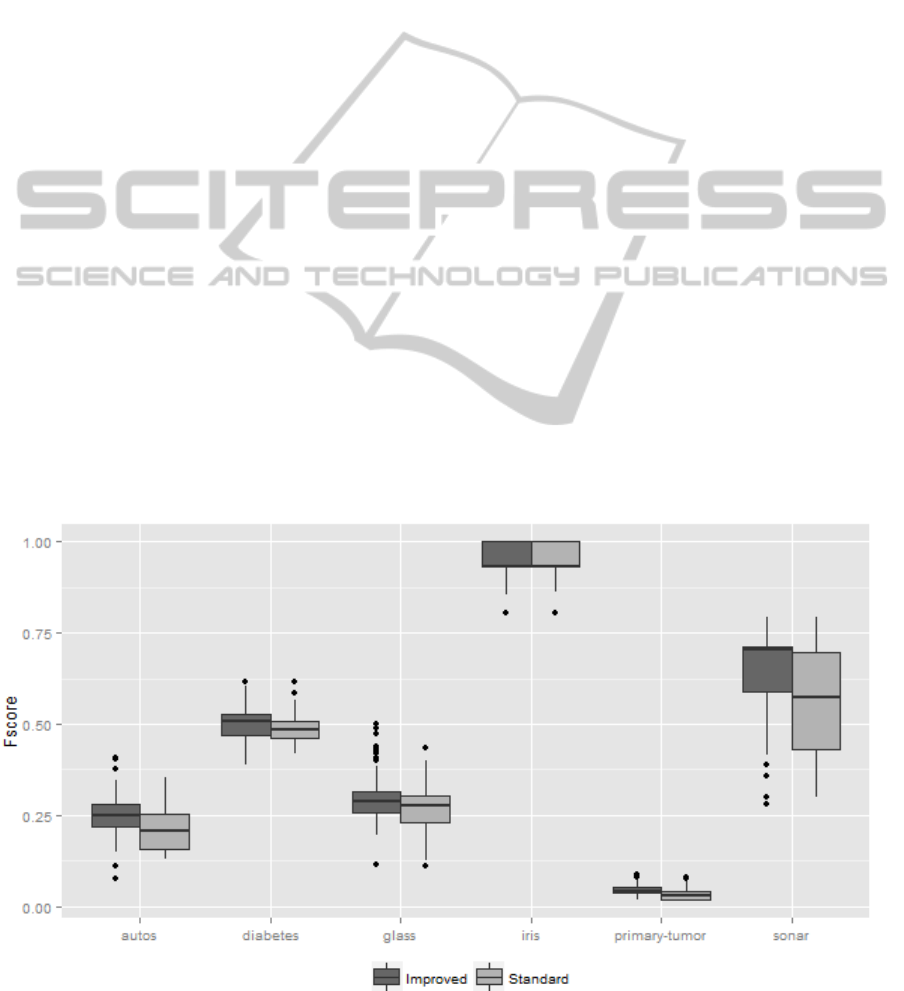
Figure 2, the same comparison is made but on the
Fscore classification metric, where our algorithm
found better average Fscore in all 6 datasets, where
5 of them are statistically significant improvements.
In 3 out of 6 dataset, our proposed algorithm
achieved better maximal Fscore and matched the
original crossover on the maximal score on 3 other
datasets. The dataset iris was an outlier here,
because both crossover methods achieved in perfect
accuracy and Fscore. As can be seen from Figure 2
no further improvement is possible on iris dataset.
This also explains why no statistically significant
improvement could be made with the iris dataset.
Let us look in details why our improvement
results in better solutions in accuracy and Fscore.
Figure 3 compares two samples (from dataset sonar),
one from each crossover, through evolution. Vertical
axis shows accuracy of the best solution in the
population. From results shown in Figure 3 we can
Figure 2: Fscore comparison between two crossovers.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
292

Figure 3: Comparison in accuracy through evolution.
see that algorithm with the standard crossover
reaches its optimum much faster than the algorithm
with our improved crossover. Figure 3 confirms that
indeed, the algorithm with standard crossover
reached its optimum already around 1400
th
generation, while algorithm with our improved
crossover continues to run for another 600
generations and reaching its optimum in generation
1860. The difference between accuracy is ~0.5 in
favour of our proposed crossover.
5 CONCLUSIONS
We proposed the innovative crossover operator that
does not choose the place for the crossover process
based at random but rather on the accuracy and
usage of the subtree. As mentioned in the overview
in the second chapter, no similar method was found
in the tree classification models. This innovative
method was tested on several datasets in our
experiment, with the results showing significant
increases in the metrics of overall classification
accuracy and average Fscore of final tree models.
Based on this we can assume that these result can be
reproduced on other classification problem datasets.
To corroborate this statement further studies are
planned on more diverse, unbalanced, and otherwise
unusual datasets. Additional research option would
be to try and replace the overall accuracy in the
evaluation of nodes with another metric such as
Fscore or similar classification or decision tree
evaluation metric.
REFERENCES
Barros, R. C. et al., 2012. A Survey of Evolutionary
Algorithms for Decision-Tree Induction. IEEE
Transactions on Systems, Man, and Cybernetics, Part
C (Applications and Reviews), 42(3), pp.291–312.
Cantu-Paz, E. & Kamath, C., 2003. Inducing oblique
decision trees with evolutionary algorithms.
Evolutionary Computation, IEEE Transactions on,
7(1), pp.54–68.
D’haeseleer, P., 1994. Context preserving crossover in
genetic programming. In Evolutionary Computation,
1994. IEEE World Congress on Computational
Intelligence., Proceedings of the First IEEE
Conference on. pp. 256–261.
Espejo, P. G., Ventura, S. & Herrera, F., 2010. A Survey
on the Application of Genetic Programming to
Classification. IEEE Transactions on Systems, Man,
and Cybernetics, Part C (Applications and Reviews),
40(2), pp.121–144.
Hengpraprohm, S. & Chongstitvatana, P., 2001. Selective
crossover in genetic programming. Population, 400,
p.500.
Iba, H. & de Garis, H., 1996. Extending genetic
programming with recombinative guidance. Advances
in genetic programming, 2, pp.69–88.
Koza, J. R., 1992. Genetic Programming: vol. 1, On the
programming of computers by means of natural
selection, MIT press.
Koza, J. R. & Noyes, J., 1994. Genetic Programming II
Videotape: The Next Generation, MIT Press
Cambridge, MA.
Majeed, H. & Ryan, C., 2006a. A less destructive, context-
aware crossover operator for GP. In Genetic
Programming. Springer, pp. 36–48.
Majeed, H. & Ryan, C., 2006b. Using context-aware
crossover to improve the performance of GP. In
Proceedings of the 8th annual conference on Genetic
and evolutionary computation. pp. 847–854.
Zhang, M., Gao, X. & Lou, W., 2007. A new crossover
operator in genetic programming for object
classification. Systems, Man, and Cybernetics, Part B:
Cybernetics, IEEE Transactions on, 37(5), pp.1332–
1343.
0,4
0,45
0,5
0,55
0,6
0,65
0,7
Standard Improved
HeuristicCrossoverOperatorforEvolutionaryInducedDecisionTrees
293
