Smooth Trajectory Generation with 4D Space Analysis for Dynamic

Obstacle Avoidance

Suhyeon Gim

1,2

, Lounis Adouane

, Sukhan Lee

and Jean-Pierre Derutin

Institut Pascal/Universit´e Blaise Pascal UMR6602, 63177, Aubi´ere Cedex, France

SungKyunKwan University, Seoburo 2066, 440-746, Suwon, Korea

Keywords:

Continuous Curvature Path, Dynamic Obstacle Avoidance, Velocity Planning.

Abstract:

This paper presents smooth trajectory generation scheme for obstacle avoidance in static and dynamic en-

vironment. The smooth trajectory has successive two steps where smooth path is generated ﬁrstly and then

corresponding velocity is planned along the path. Smooth path of continuous curvature is composed by para-

metrically adjusted clothoids with proposed algorithm and then the safe velocity planning is carried out in the

4D conﬁguration framework. Two circles are used to completely surround the used nonholonomic car-like

vehicle, this permit to check the probable future vehicle’s collisions and to have space-time analysis. Some

demonstrative simulations show the strong potential of the proposed smooth and ﬂexible methodology for

future experimentations with actual vehicles.

1 INTRODUCTION

Autonomous navigated vehicle or semi-autonomous

driver assistant system has been attracting a lot of

robotics research and industry ﬁelds for more than a

decade. One of the most important issues is trajec-

tory generation or path planning capability to manage

a safe motion in a variety of risky environments. In

path planning scheme, there are two kinds of planners

(or planning algorithm) which are characterized either

by global or local (Solea and Nunes, 2006), (Villa-

gra et al., 2012). The global path planner gives a

general navigational information (the path/trajectory

to follow) to the vehicle to go from its initial con-

ﬁguration to one ﬁnal conﬁguration while taking into

account all the obstacles in the environment (Khatib,

1986), (Giesbrecht, 2004). This planner use generally

wholly known topological or grids-composed global

map of the environment. The local path planner per-

mits for its part to obtain only the navigational infor-

mation from the current vehicle’s conﬁguration to a

ﬁnal conﬁguration, which could be not the actual ﬁ-

nal destination of the vehicle, but just un intermedi-

ate conﬁguration to avoid any obstructing obstacle.

This last planner is considered more reactive (Kelly

and Nagy, 2003), (Likhachev and Ferguson, 2009) in

the sens that it can deal easily with dynamic obsta-

cles (Chakravarthyand Ghose, 1998), (Fulgenzi et al.,

2007). It is obviously important to notice that we

could use a multitude of local planned path to obtain

the global path for the navigation (Adouane, 2013).

The work presented in this paper focuses on local

path planning algorithm with the consideration of dy-

namic obstacle avoidance. It is assumed that the ve-

hicle has a predeﬁned path from a global path planner

and the local planner is required to generate a ﬂexible

and smooth trajectory in the presence of any obstruct-

ing dynamic obstacle. The path generated from the

local path planner should be sufﬁciently accurate and

smooth to be followed by the car-like vehicle.

To obtain accurate trajectory for a car-like vehicle,

it is important for the planner to take into account:

nonholonomic contraintes of the vehicle as well as

its kinematic and dynamic contraints (Lamiraux and

Laumond, 2001). There have been a lot of smooth

path generation methods for vehicles. The works us-

ing continuous curvature path generations like those

given in (Thompson and Kagami, 2005) are very efﬁ-

cient in the sense that they take into consideration the

vehicle’s parameters as well as passenger comfort.

There have been a lot of smooth path generation

methods for the vehicle and the continuous curvature

path has been focused for its close relationship with

vehicle parameters and drivingcomfort (Montes et al.,

2007), (Labakhua et al., ).

The continuous curvature path (CCP) has some

advantages that the steering behavior of the vehicle

is closely related to the curvature variation of the path

802

Gim S., Adouane L., Lee S. and Derutin J..

Smooth Trajectory Generation with 4D Space Analysis for Dynamic Obstacle Avoidance.

DOI: 10.5220/0005148808020809

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (IVC&ITS-2014), pages 802-809

ISBN: 978-989-758-040-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

to follow and the vehicle’s movement is assured to

be smooth along all the trajectory. This trajectory is

especially useful for the nonholonomic car-like vehi-

cle and the vehicle can follow the path without ever

stopping to reorient its front wheels. The CCP for a

nonholonomic vehicle are dealt with many previous

works. Firstly, Dubins (Dubins, 1957) , Reeds-Shepp

(Reeds and Shepp, 1990) (RS path) proposed the

smooth path model for nonholonomic vehicle yield-

ing to the shortest in travel length, however it lacks the

curvature continuity. Fraichard-Scheuer (Fraichard

and Scheuer, 2004) (FS path) presented a continuous

steering planning composed by lines, circular arcs and

clothoids curves. This latter curves, with continuous

curvature, take into account upper-bounded curvature

and upper-boundedsharpness in the absence of obsta-

cles. The work of (Wilde, 2009) presented a simple

and fast trajectory generation method of continuous

curvature with minimum sharpness for human natural

and safe driving. However, the solution was limited

only for the lane change maneuver example.

In this paper, a parametric Continuous Curva-

ture Path (pCCP) which is proposed in (Gim et al.,

2014) is extended to the problem of non-zero cur-

vatures boundary conditions and it is applied to a

simple dynamic obstacle avoidance problem by us-

ing the extended-pCCP or e-pCCP. The smooth tra-

jectory generation for the static and dynamic obsta-

cle avoidance is carried out by e-pCCP paths inte-

grated with smooth velocity planning scheme. For

e-pCCP, this work has different contributions with re-

gard to the literatures. At ﬁrst, compared to FS path

(Fraichard and Scheuer, 2004), the proposed solu-

tion makes no limitation on the sharpness or curva-

ture. FS path solves the zero curvatures conﬁguration

problem while ﬁxing the sharpness in all clothoids

or uses symmetric elementary paths by replacing the

maximal curvatured arc segment of RS path with a

maximal sharpness clothoid. Another point can be

found that the nonzero curvature conﬁgurations on

both ends are dealt with for obstacle avoidance or path

replanning manouevre where initial and ﬁnal curva-

ture values are determined from current steering and

obstacle boundary modelling. The nonzero initial cur-

vature conﬁguration is useful to replan a path while

following pre-deﬁned path with nonzero steering an-

gle. The non-zero ﬁnal curvature is also important to

avoid the obstacle modeled in a bounded radius cir-

cle by generating the path for surrounding the obsta-

cle circle. The other major point is introducing 4D

conﬁguration (Wu et al., 2011) to analyze the future

vehicle’s trajectory to determine the ﬁnal avoidance

pose and velocity set-points. Compared to the ve-

locity obstacle model approach (Fiorini and Shiller,

1998), (Berg et al., 2008), (Wilkie et al., 2009), the

proposed model analyzes all the expected collision

cases for varying velocity of obstacles even for non-

straight trajectory. Resulting e-pCCP from 4D con-

ﬁguration analysis gives thus smooth trajectory even

when dealing with dynamic obstacles. This paper is

organized as follows. In the next section, the path fol-

lowing model for the nonholonomic vehicle and the

problem is deﬁned and then the proposed clothoids

solutions for the trajectory generation are described

with algorithmic description. In section 3, 4D conﬁg-

uration analysis is described with efﬁcient vehicle’s

model and the smoothing procedure for the applica-

tion to a practical implementation is addressed with

simulated results. The paper ends with a conclusion

with some prospects.

2 PATH GENERATION FOR

NONHOLONOMIC CAR-LIKE

VEHICLE

2.1 Continuous Curvature Path Model

There is a useful mathematical representation for the

nonholonomic car-like vehicle path according to its

length (curvilinear abscissa) which it uses clothoid.

A clothoid is represented by curvature variation with

the length. Fully deﬁned clothoidal form for a path is

efﬁcient for car-like vehicle in that it gives informa-

tion on the curvature along the length and it could also

give maneuvering information to the vehicle driver. A

clothoid is deﬁned by parametrical forms given by :

κ(s) = κ

+ αs, (1)

θ(s) =

κ(u)du, (2)

x(s) =

cos θ(u)du, (3)

y(s) =

sin θ(u)du, (4)

where, α is the sharpness (or rate of curvature) for

curvatureκ(s). Equation. (1) shows that the curvature

increase or decrease by constant sharpness α and the

orientation in (2) changes with integration of curva-

ture in (1). It is to be noted that this mathematical re-

lation is the same as for the physical relation between

the steering angle and the vehicle orientation where

the orientation varies in integrated amount of steering

changes. It is also noted that the position in coordi-

nate is determined only after the orientation at lengths

is calculated as in (3), (4). This means that when one

SmoothTrajectoryGenerationwith4DSpaceAnalysisforDynamicObstacleAvoidance

803

tries to ﬁnd a sharpness for a clothoid to meet the de-

sired position and orientation at a certain curvilinear

distance requires to have an analytic model of the in-

verse kinematic solution, which is not yet available in

the literature, because the problem is too complex to

resolve.

A clothoid has the property to have continuous

curvature which is either increasing or decreasing

through the length. There are some kinds of formu-

lations for the rate of the curvature such as polynomi-

als, exponential or trigonemetric function, however,

the 1

order form (like what is given in equation (1)),

relying on the constant sharpness, is well-known not

only for its computational simplicity but also for phe-

nomenal similarity to the real vehicle actuation sys-

tem. To be more speciﬁc, the curvature of a point on

the path corresponds to the steering angle of the vehi-

cle which follows the path at the point and the sharp-

ness signiﬁes the rate of the steering change at that

point. In the next subsection, the Problem deﬁnition

and algorithmic solution will be given, while begin-

ning by recalling the already proposed algorithm in

(Gim et al., 2014).

2.2 Parametric Clothoid for Path

Generation

This subsection deals with a problem to generate a

smooth path in local planner for a nonholonomic car-

like vehicle. The local planner generates a short path

in the detectable range distance and its boundary con-

dition is deﬁned by two conﬁgurations, i.e. initial

and ﬁnal P

. For CCP generation, clothoid is the

major segment along the path and each clothoid is

linked to other clothoids while satisfying boundary

conﬁgurations with attributed constraints in vehicle.

Before to explain the main contribution of the pro-

posed paper, let us remind what was already pro-

posed in (Gim et al., 2014), which consist on an

algorithmic approach to compute the parameters of

the clothoid which has as initial conﬁguration P

and

as a ﬁnal conﬁguration P

. It is to be noted that

the initial and ﬁnal speciﬁed set-poits curvatures are

equal to zero. The work considered thus the initial

and the ﬁnal steering angle of the front wheels (κ in

(1)) are always zero, which means that the vehicle

start from straight line and ﬁnish also with straight

line. The proposed algorithm in (Gim et al., 2014),

called parametricContinuousCurvaturePath (pCCP)

permits to compute these parameters based on some

basic properties or pattern of Clothoids. Indeed, when

a clothoid is deﬁned, the relations among its parame-

ters are given as following.

κ =

√

2δα, δ =

2α

, s =

2δ

, (5)

where all parameters are the values at the end

point of the clothoid and δ means the amount of ori-

entation change through the whole length which is

called deﬂection (Labakhua et al., ). Note that α, κ,

δ and s are closely related to each other and further-

more, if two of them are deﬁned, then the others are

also determined. This relation is important to make

a clothoid meet a desired pose by adjusting indepen-

dent two parameters, e.g. (α, κ) or (α,δ). To specify

the convergence criteria as well as determining initial

values for the algorithm, some basic properties or pat-

tern according to the parameter variation are useful to

understand. To summarize the links between the pa-

rameters, 3 properties can be concluded:

Property 1. As the sharpness α increases with other

parameters constant, the clothoid shrinks.

Property 2. As the deﬂection δ increases with other

parameters constant, the clothoid expands.

Property 3. As the curvature κ increases with other

parameters constant, the clothoid winds up inward.

The path in the problem requires at least two

clothoids to satisfy the both conﬁgurations where

each clothoid has a unique sharpness to adjust its cur-

vature to maximal value, i.e. C

: s 7→ [s

ℓ

]. When a

clothoid is deﬁned as C

, the other as C

and they are

composed as C

⊕C

, while satisfying the orientation

continuity G

as well as curvature continuity G

at the

connection point where G

is n-th order of Geometric

Continuity.

2.3 Problem Deﬁnition with

Algorithmic Solution

In this paper, we make a focus on the smooth local

path generation for obstacle avoidance where the ini-

tial and ﬁnal curvatures are non-zero. This problem

was not addressed in the former work (Gim et al.,

2014) and the parametric convergence criteria in the

algorithm also needs to be differently treated. An-

other importance for the problem comes from the

question on how to cope with dynamic obstacle.

When a vehicle follows the generated path for a static

obstcle, the path should be replanned with current

steering angle of initial non-zero curvature as well

as nonzero steering angle at the ﬁnal avoidance pose.

To cope with the dynamic obstacle, it needs to be ex-

tended for pCCP. The curvature for initial conﬁgura-

tion is given according to the current steering angle of

the vehicle and the curvature for ﬁnal conﬁguration

is determined from the obstacle boundary radius to

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

804

generate the path that surrounds the moving obstacle

boundary to avoid it.

To formalize the addressed problem, the following

formulation is given.

Problem: From P

,θ

,κ

) to P

,θ

,κ

)

with κ

≥ 0, κ

6= 0, ﬁnd the minimum number of

clothoids which satisfy the both conﬁgurations with

curvature continuity along the path.

Proposition 1. The conﬁguration is deﬁned on the

ﬁrst quarter plane of the Cartesian coordinates and

other conﬁgurations can be deﬁned by symmetric

manner to its X −Y coordinates. The initial pose is on

the origin with its orientation θ

= π/2 and the ﬁnal

pose exists on the ﬁrst quarter of Cartesian coordi-

nate.i.e. x > 0,y > 0.

Proposition 2. The curvature in a clothoid has posi-

tive sign when the steering angle is in the right hand

side from its middle origin, and vice versa. The sharp-

ness in a clothoid has positive sign when the steering

turns right (clockwise) noted as C

and vice versa as

With the above propositions, the pose conﬁgu-

rations of the problem can be slightly changed by



0,0,

,κ

≥ 0



and P

,θ

,κ

6= 0).

Note that there are two cases according to the turn-

ing direction or curvature sign at the ﬁnal pose.

(

> 0 : C

< 0 : C

(6)

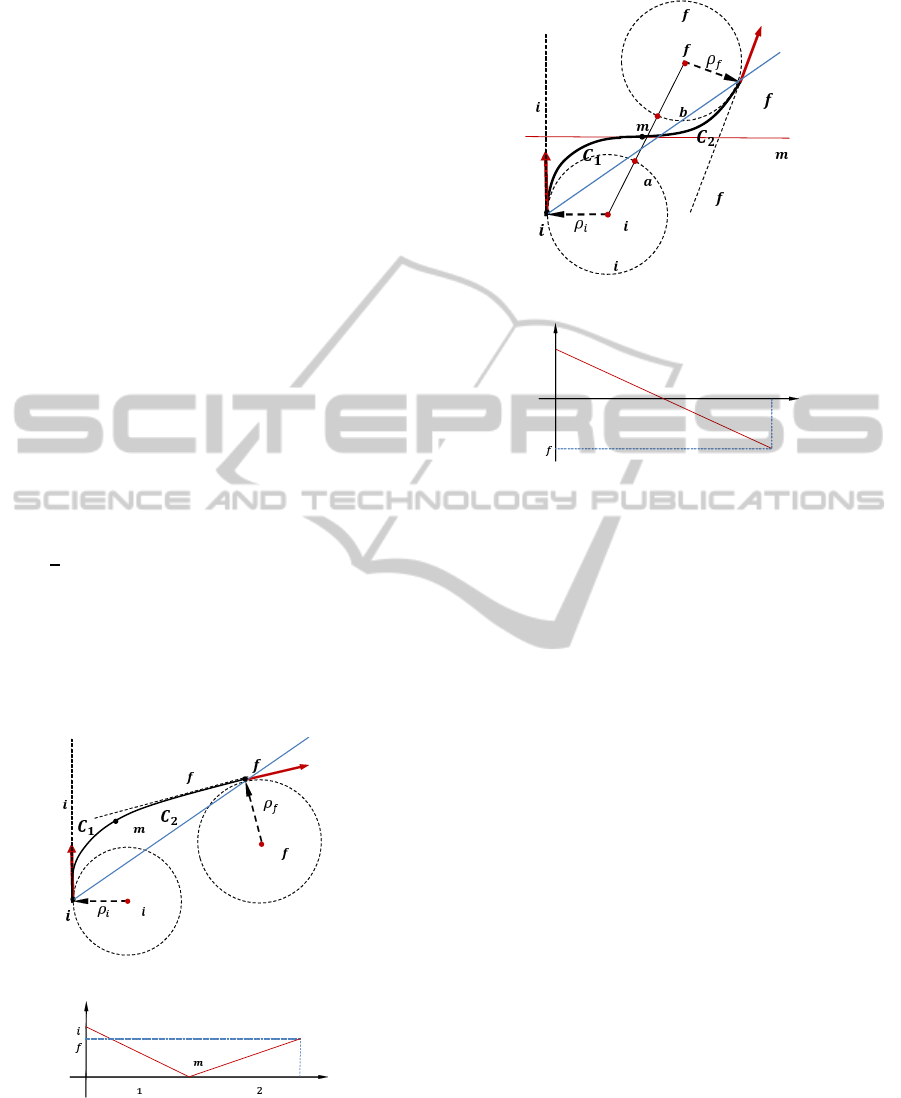
ࡼ

ℓ



ℓ



ࡼ





(a) Two clothoids composition

࡯

૚

࡯

૛

࢖

(b) Curvature diagram

Figure 1: e-pCCP problem : C

Figure 1 and Figure 2 show the path comprised by

two clothoids composition with initially same curva-

ture but with different turning direction as noted by



ࡼ

ℓ



ℓ





ℓ

ࡼ







(a) Two clothoids composition

௜

࡯

૚

࡯

૛

࢖

࢓

ଵ

ଶ

(b) Curvature diagram

Figure 2: e-pCCP problem : C

> 0 (cf. Figure 1) and κ

< 0 (cf. Figure 2) with

its corresponding curvature diagram respectively.

The initial pose P

and the ﬁnal pose P

are de-

noted by vector from each end position with given

curvatures (or radius of curvature) ρ

and ρ

where

the extension lines are displayed from each pose as ℓ

and ℓ

respectively (cf. Figure 2(a)). While fulﬁlling

the pose conﬁguration at both ends, clothoid segment

and C

(∀s ∈ [s

, s

]) are generated and located

for its ﬁnal end C

) to be P

with same orien-

tatation of ℓ

and ℓ

. The connection point p

where

each orientation and curvature are same for geomet-

ric continuity is found from a parametrical adjustment

and the point can be a line depending on the conﬁg-

uration. Corresponding curvature diagram of C

is shown in Figure 1(b) with convention described in

Proposition 2. This diagram features the steering be-

havior while following the path, in other words, the

steering turns left from the right side position to its

center and then turns right to make another right po-

sition in steering angle. Two clothoids designate two

turning motions for steering angle and it certiﬁes the

motion is continuous through all the travel length as

shown in curvature diagram.

Another case C

is shown in Figure 2. The

clothoid generation and composition procedure are

the same then the case of C

while satisfying the

conﬁguration with curvature continuity. However,

different to ﬁrst case, the solution of Figure 2(a) is

only available where there is sufﬁcient space for the

SmoothTrajectoryGenerationwith4DSpaceAnalysisforDynamicObstacleAvoidance

805

line ℓ

to pass by between two points p

, p

that

the line c

and circles r

, r

meet each other. (c

are the center position of circle r

, r

.) such that



−c



> ρ

+ ρ

as a necessary condition.

In this case, it is required that a clothoid is supple-

mented to satisfy the two clothoids conﬁguration.

ࡼ

ℓ



ℓ



ℓ

ࡼ





ℓ

(a) Three clothoids composition

௜

࡯

૙

࡯

૛

࢖

࡯

૚

଴

ଵ

ଶ

(b) Curvature diagram

Figure 3: e-pCCP problem : C

Figure 3 depicts the additional case C

in-

cluding C

where both radius of end curvatures are

overlapped so that two clothoids can not make a meet

with each other. One of feasible method to tackle

the problem is to add a clothoid which increase from

the given initial curvature κ

to any higher curva-

ture κ

as shown in Figure 3(a). The following cur-

vature diagram of (b) explains the curvature varia-

tion of three clothoids. The resulting path of three

clothoids is useful for the dynamic obstacle planning

when the current curvature is so low (including the

case κ

≃ 0) that it is expected any collision with the

obstacle which is dealt with the demonstrative exam-

ples in section 4.

The detailed procedure for generating clothoids is

described in Algorithm 1 for two clothoids C

and C

that covers the cases C

and C

of (6) .

In Algorithm 1, both end curvatures κ

, κ

are

given and initial deﬂection δ

for C

with variations

dδ,dρ are assumed by designer before entering the

loop. In line 3, the parameter is varied according

to the property found as Properties 1 to 3 and each

clothoid is generated as given in the line 4, line 6 by

(5). The variation determinant λ(C

)) for dδ is im-

portant for fast convergence with small number of it-

erations. Note that the point C

) is at the other end

of C

since the curvature value in a clothoid is varied

from 0 to its maximum κ

max

by s

to s

ℓ

variation. The

rule for determining the sign of dδ is deﬁned by an in-

equality condition which checks on the point p(x,y)

whether it locates in upper or lower side of the tan-

gential line at p

) as following.

λ(p, p

) = −tan(θ

−δ

)x+ y+ x

+ tan(θ

−δ

(7)

where it is a straight line passing the end point

of a clothoid C

, i.e. C

) and λ(C

)) is checked

for the location on the pointC

) = (x,y)|C

,s = s

The other determinant equation is λ

⊥

which is the per-

pendicular line of λ(C

)) which is described as,

⊥

(p, p

) = x−x

−tan(θ

−δ

+ tan(θ

−δ

)y.

(8)

The composition of two clothoids by given con-

straints requires only one adjusting variable for solv-

ing the problem and there are unsolvable conﬁgura-

tions only by regulating the variable such as the end

point of C

locates inside of the ﬁnal radius of cur-

vature circle r

. In such case, additional regulation

is performed to make two clothoids meet by reducing

the radius ρ

(or increasing the curvature) at the ﬁnal

pose as described in line 13. The convergence toward

the solution is deﬁned in line 4 where D

, the distance

between the composed curve C

1,2

and ℓ

reach the

threshold ε, e.g. 10

−3

[m].

Algorithm 1: e-pCCP generation.

Require: δ

,dδ, dρ

1: procedure CLOTHOID2NC(P

)

while D

≤ ε do ⊲ Dist. C

) to ℓ

= (δ

+ dδ)

4: α

← f (κ

,δ

) ⊲ C

generation

= θ

−θ

−δ

⊲ G

continuity

6: α

← f

′

(κ

,δ

) ⊲ C

generation

← ℓ

)

8: dδ = sign(λ)|dδ|

if λ(C

))

λ < 0 then

10: dδ = dδ/2

11:

end if

12: if λ

⊥

))

⊥

< 0 then

13:

= ρ

−dρ ⊲ ρ

reduction

14: end if

15:

λ = λ,

⊥

= λ

⊥

16: end while

17:

C ←C

⊕C

⊲ Composition: ⊕

18:

return

sol

) ⊲ Obtained Solution

19: end procedure

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

806

3 VELOCITY PLANNING IN 4D

SPACE

3.1 4D Space Analysis for Obstacle

Avoidance

In this subsection, a framework of 4D space is in-

troduced to analyze collision detection in space and

time domain and to plan the obstacle avoidance ma-

neuver for a vehicle. Cartesian coordinated 3D con-

ﬁguration space (C-space) with additional time axis

are constructed to analyze future status for dynamic

objects. A representative description is shown in Fig-

ure 4 where two vehicle move in each direction and

expected to make collision on intersection at a colli-

sion time t

by meeting the two future trajectory lines

and L

. It is shown that an obstacle vehicle moving

in velocity v

and a vehicle of v

collide at the state

in 4D space. In 4D space, it is easy to check on any

possible collision among dynamic objects by measur-

ing minimum distance between each future trajectory

line whether the resultant value is less than a collision

threshold distance where the threshold is bounded by

object modeling scheme.

With 4D analysis and circular representation for

the vehicle, feasible avoidance pose can be deter-

mined to avoid any collision by replanning the trajec-

tory. One of possible avoidance plan is to modify the

velocity proﬁle by encompassing the collision bound-

ary with minimal changes of original velocity proﬁle.

The other possible avoidance consists to set up the

arrival pose of the future generating path to be safe

from any collision. For the dynamic obstacle avoid-

ance, here, two avoidance poses (front and rear) are

considered as follows.

Figure 5 presents the collision plane of the ob-

stacle where the horizontal axis corresponds to the

conﬁguration space C and vertical axis presents fu-

ture time. Consistent with the problem deﬁnition,

the obstacle is assumed to move from left side of

Figure 4: 4D conﬁguration analysis for collision avoidance.

Obstacle

ࡼ

ࢉ

ࡼ

ࢌࢇ

ࡼ

࢘ࢇ

࢚

ࢉ

࢚

ࡿ

ࢉ

ࡸ

ࢌ

ࡸ

࢘

ത

ഥ

Figure 5: Avoidance pose planning in collision plane.

the line ℓ

(cf. Figures 1,2 and 3) to right side with

constant velocity (same speed and orientation) at t

This methodology remains effective when the obsta-

cle changes its orientation or speed such that replan-

ning is started as the change is detected. At the posi-

tion of P

in t

, a collision is expected at the state S

In the plane, there are two avoidance modes accord-

ing to the location of the obstacle boundaries. Upper

region of the boundary, noted as L

corresponds to

front avoidance region and lower part of the bound-

ary L

corresponds to rear avoidance. The avoidance

pose (or ﬁnal pose) P

is determined to be the point on

the tangential line which is perpendicular to obstacle

velocity direction. According to the avoidance pose,

the path by the vehicle is C

for L

andC

for L

avoidance.The vehicle is represented by two circles in

this work to simply check the collision distance with

obstacles. When the obstacle comes close to collide

with the vehicle from the right side to left of ℓ

(cf.

Figures 1,2 and 3), the avoidance modes are changed

each other with the same scheme. Under two avoid-

ance shemes of velocity replanning and path replan-

ning, there are four avoidance statuses

, F

and

where every subscript signiﬁes colliding obstacles

(circle) with one of the two circles (which surround

the vehicle).

Note that

in velocity change avoidance lo-

cate at the vertical line of P

where both circles pass

by the expected collision position P

but with arrival

time differences. For the path replanning, it requires

another stragegy to constrain the arrival time at rear

avoidance arrival pose P

or front avoidance arrival

pose P

. In what follows, the strategy to locate the

collision time t

to be out of the obstacle boundary is

to ﬁnd the time at avoidance pose F

or R

which are

in the same level of t

as well as being closest to the

obstacle boundary. In the avoidance maneuver, the

initial velocity at t

could be maintained with a little

changes according to the changes in the travel length

of the new replanned path.

3.2 Dynamic Obstacle Avoidance

With the obtained solution for path planning, using

SmoothTrajectoryGenerationwith4DSpaceAnalysisforDynamicObstacleAvoidance

807

clothoids given in section 2.3, it is proposed in this

section to apply it for dynamic obstacle avoidance

problem. In the dynamic obstacle problem, the ob-

stacle is represented with a circle (Chakravarthy and

Ghose, 2011) having constant velocity.

With the conﬁguration described in section 2.3, e-

pCCP to avoid obstacles is generated.

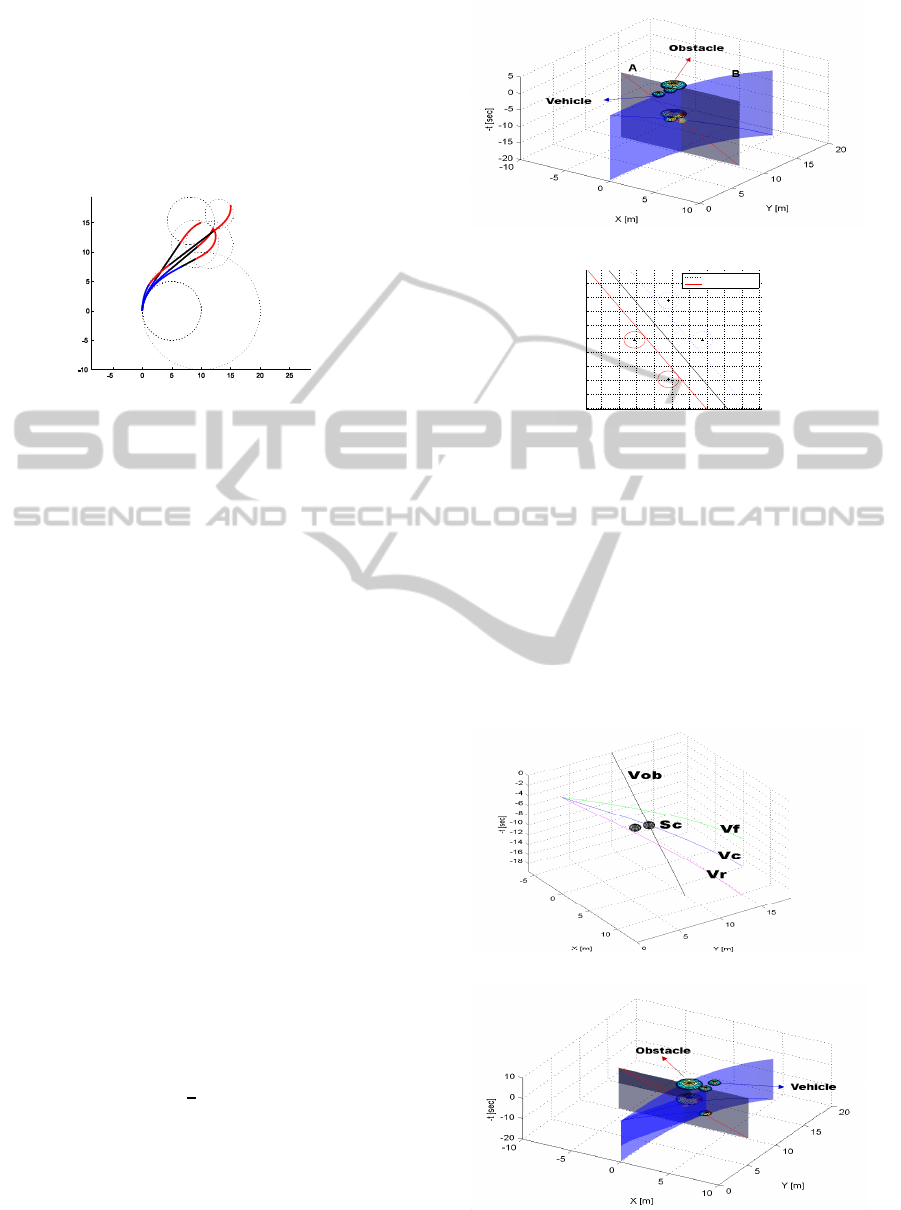
Figure 6: e-pCCP for obstacle avoidance.

In Figure 6, four different conﬁgurations are ap-

plied for e-pCCP generation. Each generated path sur-

round the obstacle circle to avoid the obstacle by path

following. The initial conﬁguration and ﬁnal conﬁgu-

ration are denoted by P

and P

while the correspond-

ing radius of curvatures are presented respectively.

The generated paths are composed by two clothoid

with additional straight line to have curvature conti-

nuity while avoiding the obstacle boundary as close

as possible. This avoidance path has additional ad-

vantages as follows. At ﬁrst, the path could be short

accoring to the static or dynamic obstacle. Secondly,

the rate of steering turn (or sharpness) is minimal

compared to farther pose avoidance from the obsta-

cle. Lastly, such path could be still efﬁcient when the

obstacle changes its moving direction while avoidng

since the path could be also regenerated with current

steering angle as initial curvature and new ﬁnal con-

ﬁguration by expected obstacle motion. Obtained e-

pCCP is applied in 4D conﬁguration space in order

that the path combines the velocity smoothness for

dynamic obstacle to fulﬁll the continuous trajectory

of vehicles.

Figure 7 presents a demonstrative 4D space sim-

ulation for dynamic obstacle avoidance. In (a), the

obstacle trajectory of A plane and the vehicle trajec-

tory of B plane are plotted in the space by given infor-

mation for the obstacle P

(−6,10,0, 0) with 0.6 m/s

and the vehicle P

(0,0,

,0.08). In this conﬁgura-

tion, a collision is predicted at 10 sec in future and (b)

depicts the obstacle avoidance poses determination as

described in Figure 5.

Figure 8 shows the replanned trajectory for the

simulation given in Figure 7 where (a) is the velocity

replanning and (b) is the replanned path by e-pCCP.

In (a), collision state S

is shown along the trajec-

(a) Collision case

3 4 5 6 7 8 9 10 11 12

−15

−14

−13

−12

−11

−10

−9

−8

−7

−6

Travel length [m]

Elapsed time [−sec]

Front avd.(Rear circle)

Rear avd.(Front Circle)

(b) Avoidance planning

Figure 7: 4D analysis for dynamic obstacle avoidance.

tory line v

with obstacle trajectory v

. For the ve-

hicle, the front avoidance with current velocity v

and

rear avoidance with current velocity v

are planned

while both avoidance trajectories keep the safe dis-

tance to avoid any collosion with the obstacle trajec-

tory. Figure 8(b) demonstrates that the generated tra-

jectory guarantees a smooth collision avoidance with

the dynamic obstacle.

(a) Velocity replanning

(b) Safe trajectory

Figure 8: e-pCCP for obstacle avoidance.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

808

4 CONCLUSIONS

This paper presents a smooth trajectory generation for

dynamic obstacle with 4D space analysis and e-pCCP.

Extending pCCP to the nonzero curvatures problem

permits the generated path to be reactive for dynamic

obstacle. By collision checking in 4D space analysis

with two circles vehicle representation for the vehicle,

the avoidance poses are determined to avoid any risk

of collision on the future. The resultant trajectory has

steering smoothness on the path as well as smooth ve-

locity changes along the path. Demonstrative exam-

ples on a dynamic obstacle shows the effectiveness

of the proposed methods and expected to be imple-

mented for more complicated dynamic environments

such as multiple obstacles or cluttered areas with real

time performance.

REFERENCES

Adouane, L. (2013). Toward smooth and stable reactive mo-

bile robot navigation using on-line control set-points.

In IEEE/RSJ, IROS’13, 5th Workshop on Planning,

Perception and Navigation for Intelligent Vehicles,

Tokyo-Japan.

Berg, J. V., Lin, M., and Manocha, D. (2008). Recipro-

cal velocity obstacles for real-time multi-agent navi-

gation. IEEE Int. Conf. on Robotics and Automation,

pages 1928–1935.

Chakravarthy, A. and Ghose, D. (1998). Obstacle avoidance

in a dynamic environment: A collision cone approach.

IEEE trans. on Systems, Man and Cybernetics-Part A:

Systems and Humans, 28(5):562–574.

Chakravarthy, A. and Ghose, D. (2011). Collision cones

for quadric surfaces. IEEE Trans. on Robotics,

27(6):1159–1166.

Dubins, L. E. (1957). On curves of minimal length with a

constraint on average curvature, and with prescribed

initial and terminal positions and tangents. American

Journal of Mathematics, 79:497–516.

Fiorini, P. and Shiller, Z. (1998). Motion planning in dy-

namic environments using velocity obstacles. Int. J.

of Robotics Research, 17(7):760–772.

Fraichard, T. and Scheuer, A. (2004). From Reeds and

Shepp’s to continuous curvature paths. IEEE Trans.

on Robotics, 20:1025–1035.

Fulgenzi, C., Spalanzani, A., and Laugier, C. (2007). Dy-

namic obstacle avoidance in uncertain environment

combining pvos and occupancy grid. IEEE Int. Conf.

on Robotics and Automation, pages 1610–1616.

Giesbrecht, J. (2004). Global path planning for unmanned

ground vehicles.

Gim, S., Adouane, L., Lee, S., and Derutin, J.-P. (2014).

Parametric continuous curvature trajectory for smooth

steering of the car-like vehicle. Int. Conf. on Intelli-

gent Autonomous Systems.

Kelly, A. and Nagy, B. (2003). Reactive nonholonomic

trajectory generation via parametric optimal control.

The International Journal of Robotics Research, 22(7

- 8):583 – 601.

Khatib, O. (1986). Real-time obstacle avoidance for ma-

nipulators and mobile robots. The int. J. of Robotics

Research, 5(1):90–98.

Labakhua, L., Nunes, U., Rodrigues, R., and Leite, F. S.

Smooth trajectory planning for fully automated pas-

sengers vehicles: Spline and Clothoid based methods

and its simulation.

Lamiraux, F. and Laumond, J. P. (2001). Smooth mo-

tion planning for car-like vehicles. IEEE Trans. on

Robotics and Automation, 17(4):498–501.

Likhachev, M. and Ferguson, D. (2009). Planning long dy-

namically feasible maneuvers for autonomous vehi-

cles. Int. Journal of Robotics Research, 28(8):933–

945.

Montes, N., Mora, M. C., and Tornero, J. (2007). Tra-

jectory generation based on rational Bezier curves as

clothoids. IEEE Intel. Vehicles Symposium, pages

505–510.

Reeds, J. A. and Shepp, L. A. (1990). Optimal paths for

a car that goes both forwards and backwards. Paciﬁc

Journal of Mathematics, 145(2):367–393.

Solea, R. and Nunes, U. (2006). Trajectory planning with

velocity planner for fully-automated passenger vehi-

cle. Intel. Transportation Systems Conf., pages 474–

480.

Thompson, S. and Kagami, S. (2005). Continuous curva-

ture trajectory generation with obstacle avoidance for

car like robot. Int. Conf. on Computational Intelli-

gence for Modeling, Control and Automation, pages

863–870.

Villagra, J., Milantes, V., Perez, J., and Godoy, J. (2012).

Smooth path and speed planning for an automated

public transport vehicle. Robotics and Autonomous

Systems, 60:252–265.

Wilde, D. K. (2009). Computing clothoid segments for

trajectory generation. IEEE/RSJ Int. Conf. on Intel.

Robots and Systems, pages 2440–2445.

Wilkie, D., van den Berg, J., and Manocha, D. (2009). Gen-

eralized velocity obstacles. IEEE Int. Conf. on Intelli-

gent Robots and Systems, pages 5573–5578.

Wu, P. P. Y., Campbell, D., and Merz, T. (2011). Multi-

objective four-dimenstional vehicle motion planning

in large dynamic environments. IEEE Trans. on

Systems, Man, and Cybernetics-Part B:Cyberntetics,

41(3):621–634.

SmoothTrajectoryGenerationwith4DSpaceAnalysisforDynamicObstacleAvoidance

809