
Extraction of Dynamics-correlated Factors from Image Features in
Pushing Motion of a Mobile Robot
Takahiro Inaba and Yuichi Kobayashi
Graduate School of Engineering, Shizuoka University, 3-5-1 Johoku, Naka-ku, Hamamatsu, Japan
Keywords:
Bio-inspired Robotics, Developmental Robotics, Image Feature Extraction, Motion Learning.
Abstract:
It is important for autonomous robots to improve capability of extracting information that is relevant to their
motions. This paper presents an extraction and estimation of factors that affect behavior of object from image
features in object pushing manipulation by a two-wheeled robot. Motions of image features (SIFT keypoints)
are approximated with variance. By detecting correlation between the variance and positions of the keypoints,
the robot can detect keypoints whose positions affect behaviour of some keypoints. Position information of
the keypoints is expected to be useful for the robot to decide its pushing motion. The proposed scheme was
verified in experiment with a camera-mounted mobile robot which has no pre-defined knowledge about its
environment.
1 INTRODUCTION
In recent years, autonomous robots are expected to
act in more various environment, ranging from house-
hold to disaster site, outdoor, and so on. In such kinds
of environment, many unknown factors will prevent
the robots from accomplishing their tasks. For exam-
ple, in a situation where a robot is needed to move
an unknown object, it is very difficult to give pre-
programmed plan to the robot about where to push
the object with which direction because its motion de-
pends on various factors such as shape, weight, stiff-
ness, inertia and so on.
Immediate solution for this problem is to
once avoid pursuing autonomy and apply human-
controlled robots, but another approach can be to de-
velop learning ability of autonomous robots to build
recognition and motion-planning strategy by their
own. Developmental robotics (Asada et al., 2009)
is closely related to the above-mentioned approach
since it aims to build not only motion learning abil-
ity (using reinforcement learning (Sutton and Barto,
1998) for example) but also recognition of environ-
ment while considering connection between recogni-
tion and robot’s motion (Metta and Fitzpatrick, 2003).
As an example of recognition of environment,
let’s consider a case where a robot is going to manip-
ulate an object. It will be important to know whether
the robot can be push it, how it moves when the robot
manipulates it, and what kind of factor causes its be-
havior. Developmental robotics deals with acquisition
of such kind of information through leaning.
Madokoro et al. proposed recognizing and iden-
tifying an object by using visual sensor (Madokoro
et al., 2012). After unsupervised learning using im-
ages collected in advance, robot recognizes the ob-
ject using camera information. Nakamura et al. pro-
posed a multi-modal object categorization by pLSA
(probabilistic Semantic Analysis) and LDA (Latent
Dirichlet Allocation), that are applied to information
obtained when robot manipulates objects (Nakamura
et al., 2007). In this research, robot grasps objects
and observes them from various angles and it clas-
sifies object and estimate behavior of a new object.
Nishide et al. proposed motion generation of object
manipulation by applying a neural network to obtain
information when robot manipulates object (Nishide
et al., 2008).
In the researches mentioned above (Nakamura
et al., 2007) (Nishide et al., 2008), how the robot
should behave was given by human designers. But
in order to construct ability of behavior generation,
it is desirable to let the robot plan its behavior based
on its trial and error instead of giving the robot mo-
tion information (time series of joint angle, for ex-
ample). Another common problem for the related re-
searches (Madokoro et al., 2012) (Nakamura et al.,
2007) (Nishide et al., 2008) is that extraction of im-
portant factors that are influential to the robot’s inter-
est is made only as a result of a large-scale learning
process, sometimes almost as a black box. For flexi-
ble motion generation, it is important to extract partial
310
Inaba T. and Kobayashi Y..
Extraction of Dynamics-correlated Factors from Image Features in Pushing Motion of a Mobile Robot.
DOI: 10.5220/0005154003100315
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 310-315
ISBN: 978-989-758-054-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

dependencies between sensor observation. Therefore,
construction of recognition based on robot’s simple
and elemental behaviors in a manner where relations
among factors of sensor information are tractable, has
not been realized yet.
This paper presents a method of extracting corre-
lation between features obtained by sensor informa-
tion based on elementary behavior of robot. Pushing
motion of a mobile robot is considered as a task. In
the process of pushing motion, image features that are
relevant to changes of object behavior are extracted.
The remainder of the paper is constructed as fol-
lows. Problem settings are described in Section 2. Ex-
traction of factors related to dynamics of observation
is described in Section 3. Experiment is explained in
Section 4, followed by conclusion conducted with a
mobile robot.
2 PROBLEM SETTING
The experimental settings are depicted in Fig.1(a) and
Fig.1(b). A mobile robot equipped with a camera
(Fig.1(a)) moves on the floor while sometimes touch-
ing an object that is randomly located in its environ-
ment. The object will move according to the motion
of the robot when they are contacting with each other.
Examples of images captured by its camera are de-
picted in Fig.2, where part of the object is viewed in
the image when robot is closely located to the object
or is contacting with it.
It is assumed that size, shape, appearance of the
object and as well as appearance of background are
unknown to the robot. An implicit assumption for
the object is that the object provides more than sev-
eral SIFT (Scale Invariant Feature Transform) (Lowe,
2004) keypoints so that motion of the object can be
detected by the keypoints corresponding to the object.
Control input given to the robot is desired veloci-
ties of the both wheels. Observation of the robot is
images obtained at every frame. Both control and
observation frames are one sec. Image features are
obtained from each image as SIFT keypoints at a
frame and correspondences with its preceding frame
for each image are calculated by mean shift (Co-
maniciu et al., 2002). Mean shift algorithm is used
to classify SIFT keypoints because feature value of
SIFT keypoints changes gradually, and thus conven-
tional SIFT matching algorithms do not work effec-
tively. Process of classifying SIFT keypoints is de-
picted in Fig.3. Each keypoint extracted in an image
has 128 dimension feature vector V = [v
1
···v
128
]((1)
in Fig.3). SIFT uses luminance gradient around key-
point for description of feature vector. SIFT divides
(a) Mobile robot with CCD camera. (b) Robot, object and environment
Figure 1: Problem settings.
area around keypoint to 16 area, and creates eight his-
togram of luminance gradient in every 45 degrees in
each divided area. This 128 histograms are used as
components of the feature vector. Mean shift is ap-
plied to V. As a result, keypoints that have close fea-
ture vectors are classified into a common cluster((2)
in Fig.3). Matching of the keypoints between two im-
ages is decided whether two keypoints belong to the
same cluster((3) in Fig.3). Thus, not only position but
displacement from its preceding frame is available as
observation.
Finally, it is desirable that the robot system is to be
able to plan how to approach to the object and push it
when a target position of the object is given to the
robot. For this goal, the robot first must be able to
identify which part of image should be focused for
the planning. In other words, the robot first needs
to detect keypoints whose positions are influential to
the behavior of the object. In this paper, we describe
about extracting correlation between object behavior
(a) Robot at the center of object. (b) Robot at the right edge of object.
Figure 2: Examples of obtained image.
i keypoint has 128 dimension feature
vector V
i
(1) Extraction keypoints
from each image.
(2) Using mean shift, key
points are classified by
each V
i
.
(3)Key points between
images can be matched by
result of mean shift.
Figure 3: Process of classifying keypoints.
ExtractionofDynamics-correlatedFactorsfromImageFeaturesinPushingMotionofaMobileRobot
311
and position of keypoints in order to find keypoints
that are useful for estimating the object behavior with-
out any knowledge on the environment.
3 EXTRACTION OF
DYNAMICS-CORRELATED
FACTORS
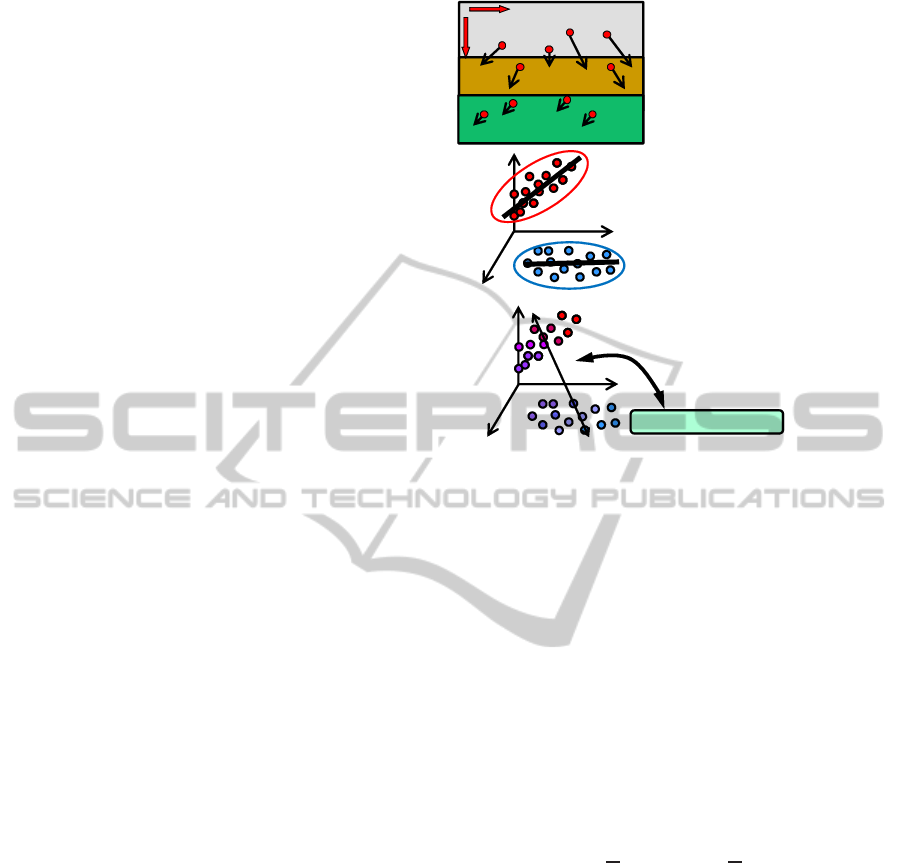
3.1 Outline
Outline of the proposed extraction of dynamics-
correlated factors from image features is depicted in
Fig.4. Image features are extracted by SIFT key-
points, as show in (1) in Fig.4. Motions of features
in the image frame are approximated as a function of
motor command to the robot wheels. NGnet (Nor-
malized Gaussian networks) (Moody and Darken,
1989) is applied for the approximation so that vari-
ance of motion of features can be clustered by multi-
ple Gaussian distributions around linear function ap-
proximators ((2) in Fig.4). NGnet is adopted be-
cause it provides not only function approximation
but also estimation of variance. Gaussian process
is widely used for function approximation with esti-
mation of variance (Rasmussen and Williams, 2006),
but it deals with only uniform variance in its gen-
eral form. An extension of Gaussian Process to
deal with input-dependentvariance has been proposed
(LLazaro-Gredilla and Titsias, 2011), but its calcula-
tion amount is high.
The variance of motion of features is evaluated
as class probabilities to the clusters using LDA (Lin-
ear Discriminant Analysis) ((3) in Fig.4). The clus-
ters used for LDA correspond to the Gaussian dis-
tributions composing NGnet. In comparison with
PCA(Principal Component Analysis), LDA is more
suitable for extracting dynamics-correlated factors
since if NGnet appropriately reflects variance of dy-
namics through its function of clustering. Dynamics-
correlated factors are extracted by analyzing correla-
tion between the class probabilities and position of
each keypoint. In this paper, we use CCA (Canoni-
cal Correlation Analysis) for calculating correlation.
CCA is one of multivariate analysis method. Us-
ing CCA (Canonical Correlation Analysis), where
keypoints with large correlation coefficient can be
regarded to be dynamics-correlated factors ((4) in
Fig.4).
x
y
Object
Landscape
Floor
i keypoint
i
x∆
x∆
y∆
O
φ
x∆
y∆
O
φ
P
(1) Function approximation for
dynamics of keypoint.
)(
φ
f
i
=∆x
(2) Clustering of keypoint dynamics
using NGnet.
(3) Calculated class probabilites by
LDA.
(4) CCA(correlation extraction).
x
: Position of keypoint
Figure 4: Outline.
3.2 Collection of Motions of Keypoints
and Motor Commands
The mobile robot pushes object with various move-
ments. Images before and after each motion of the
robot are captured by its camera. SIFT keypoints are
extracted in the images and matching is applied to be-
tween the two frames. Fig.5 shows an example of mo-
tions of keypoints after one cycle of robot’s locomo-
tion.
Let m
l
, m
r
∈ R [step/s] denote command of rota-
tional speed to the left and right wheels, respectively.
Motor command to the robot is denoted by φ ∈ R,
where φ specifies the rotational speeds m
r
and m
l
as
m
r
=
C
2
− φ, m
l
=
C
2
+ φ, (1)
where C ∈ R is a constant. Fig.6(a) shows examples
of trajectories of robot with different values of φ. All
128-dimensional feature vectors of SIFT keypoints
over the collected images are clustered by mean shift
algorithm. Matching of keypoints between two im-
age frames is applied based on information of the ob-
tained clusters. Let i, i = 1, ··· , N denote index of
keypoint, where N denotes the total number of key-
points identified by the clustering procedure. Position
of keypoint i in the image coordinate is denoted by
x
x
x
i
∈ R
2
and its motion vector after the robot’s loco-
motion is denoted by ∆x
x
x
i
∈ R
2
.
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
312

Figure 5: Example of motions of keypoints.
0=
φ
0<
φ
0>
φ
(a) Trajectory of robot
x
y
ԥx
ԥy
䠖
Key point extracted from image before move
䠖
Key point extracted from image after move
䠖
Trajectory of key point
(b) Example of feature points data
Figure 6: Example of collecting data.
3.3 Identification of Environmental
Dynamics by NGnet
Once keypoints are clustered by mean shift, motion of
each keypoint is approximated by NGnet, which con-
sists of Gaussian mixture model with linear approxi-
mators, as a function of φ as ∆x = f(φ). Approxima-
tion of NGnet is based on EM algorithm (McLachlan
and Krishnan, 2008).
3.4 Calculation of Class Probability by
LDA
LDA is applied to the multiple classes obtained by
NGnet. LDA is dimensionality reduction method
that maximizes the variance between classes. Aver-
age of ∆X is ∆
¯
x. Let ∆x
k, j
∈ ∆X
j
denote motion of
k-th(k = 1, ··· , n) keypoint in class j( j = 1, · · · , M),
where ∆X
j
denotes set of motion vectors of keypoints
in class j and n
j
. Within-class variance W and inter-
class variance B are obtained by the following equa-
tion.
W =
1
n
C
∑
i=1
∑
∆x∈∆X
i
∆x− ∆
¯
x
i
∆x− ∆
¯
x
i
T
(2)
B =
C
∑
i=1
n
i
∆x− ∆
¯
x
i
∆x− ∆
¯
x
i
T
(3)
For discrimination of between two classes, it is nec-
essary that W is as small as possible and B is as big
as possible. a defines transformation matrix for re-
ducing dimension of ∆X, and evaluation function for
separation between classes J(a) defines as following
equation,
J(a) =
a
T
Ba
a
T
Wa
. (4)
Vector a that maximizes J(a) is obtained as eigenvec-
tor of matrix W
−1
B. Linear discriminant coefficients
vector d is also calculated based on the obtained vec-
tor a. Using this result, class probability of i-th key-
point P
i
is estimated by P
i
= exp(∆bfx
i
d
T
).
3.5 Extraction of Correlation by CCA
CCA is used to extract keypoints whose positions are
relevant to the change of motion dynamics. CCA is
applied to class probability and position of keypoint,
and correlation coefficient r is obtained. Correlation
between positions of keypoints and their class prob-
abilities are analyzed using CCA. Let P
i
, i = 1, ··· , n
be defined by P
i
= P( j|∆x
i
), where class is specified
as j = 1 and M = 2 for simplicity. Data matrices for
CCA is defined as P = [P
1
··· P
n
], X = [x
1
··· x
n
]
T
.
Each weight coefficient of synthetic linear variable U,
V is a ∈ R
2×1
, b ∈ R
1×1
, and U, V is obtained by fol-
lowing equation,
U = aX (5)
V = bP. (6)
r is obtained by following equation, then a and b is
determined to value that r is maximum,
r =
Cov[U, V]
p
Var[U]
p
Var[V]
, (7)
where Cov denotes covariance and Var denotes vari-
ance.
4 EXPERIMENT
In the experiment, robot was placed in front of the
object and given control input while changing φ in
{−20, −15, −10, 0, 10, 15, 20}. The initial positions
ExtractionofDynamics-correlatedFactorsfromImageFeaturesinPushingMotionofaMobileRobot
313
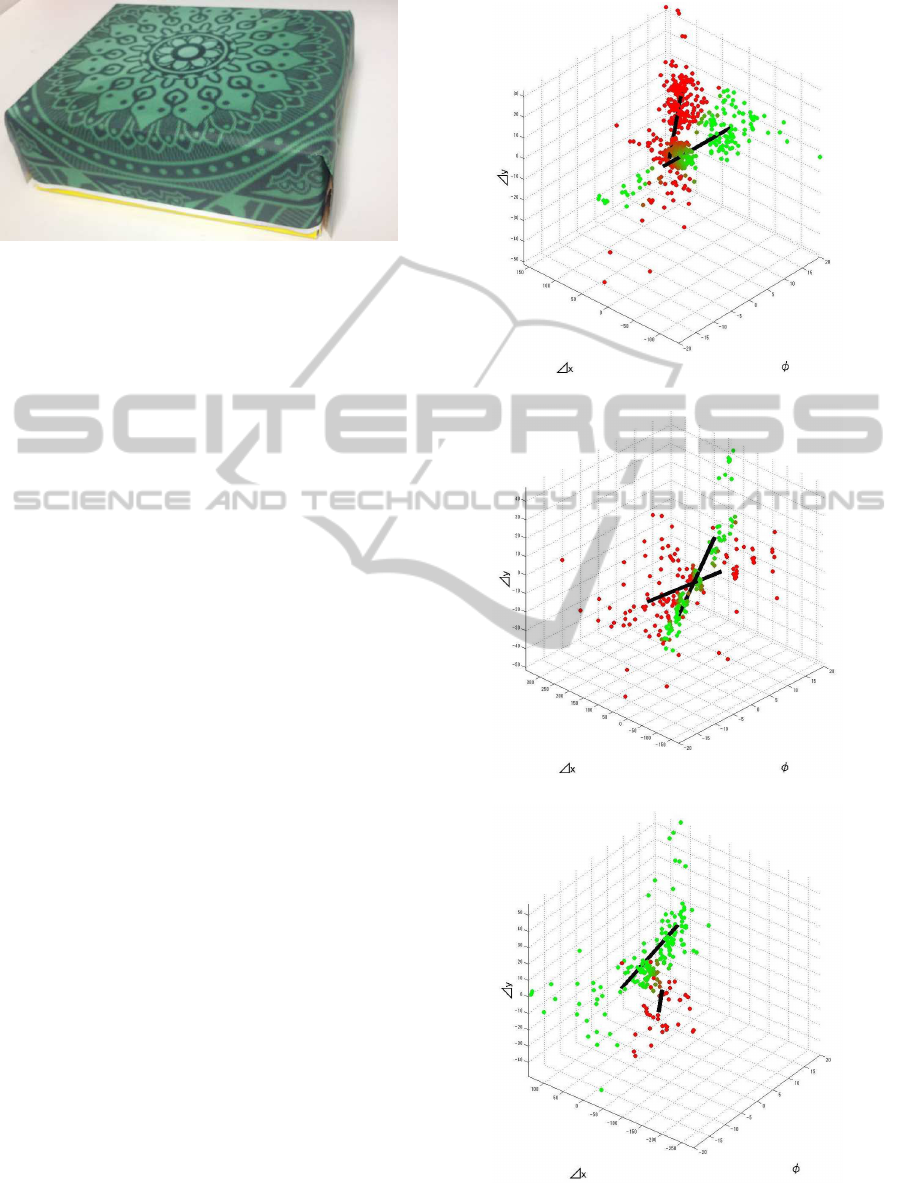
Figure 7: Object.
for the robot were either the center of the object (see
Fig.7) or right edge of it. As a result of clustering
by mean shift, totally 234 keypoints were obtained,
24 for the object and 210 for background. Pushing
behavior were conducted over 100 times. Results of
approximation and classification by NGnet are shown
in Fig.8, with M = 2. Colors of points denote classes,
and straight lines denote approximated linear func-
tions, each corresponding to a class. It can be seen
that in 8(a) and 8(b) of Fig.7, distribution of ∆x
i
could
be properly estimated by two distributions. On the
other hand, for some keypoints, classification into two
classes was not properly done as shown in 8(c) of
Fig.8, for example. This will be a cause of failure
of extraction of correlation.
Distribution of correlation coefficients of key-
points for the object and background is depicted in
Fig.9. As a whole, keypoints on the object showed
higher correlation in comparison with those on back-
ground. It means that points on the object are more
reliable to predict motions of (not necessarily, but
mainly) the object. Keypoints that have high and low
correlation coefficient are depicted in Fig.10. Red
points denote keypoint that has high correlation, and
green ones denote keypoint that has low correlation.
It can be seen that keypoints with correlation are
commonly extracted at the object with constantly-
tractable positions in the image.
Estimated motions of keypoint of the two classes
are depicted in Fig.11. Red arrow depicts motion of
keypoint when robot pushed center of the object by
φ = 0, and blue one depicts motion of keypoint when
robot pushed right edge of the object by φ = 0. It
can be seen that depending on the position of the key-
point, different directions of motion were predicted.
It means that the robot can predict which direction
the object moves depending on the position of a reli-
able keypoint. This prediction will help the robot to
plan its action so that it can move the object to a de-
sired location. For the purpose of prediction, errors in
the process of variance approximation and correlation
analysis should be further investigated.
(a) Result of NGnet 1.
(b) Result of NGnet 2.
(c) Result of NGnet 3.
Figure 8: Result of NGnet.
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
314
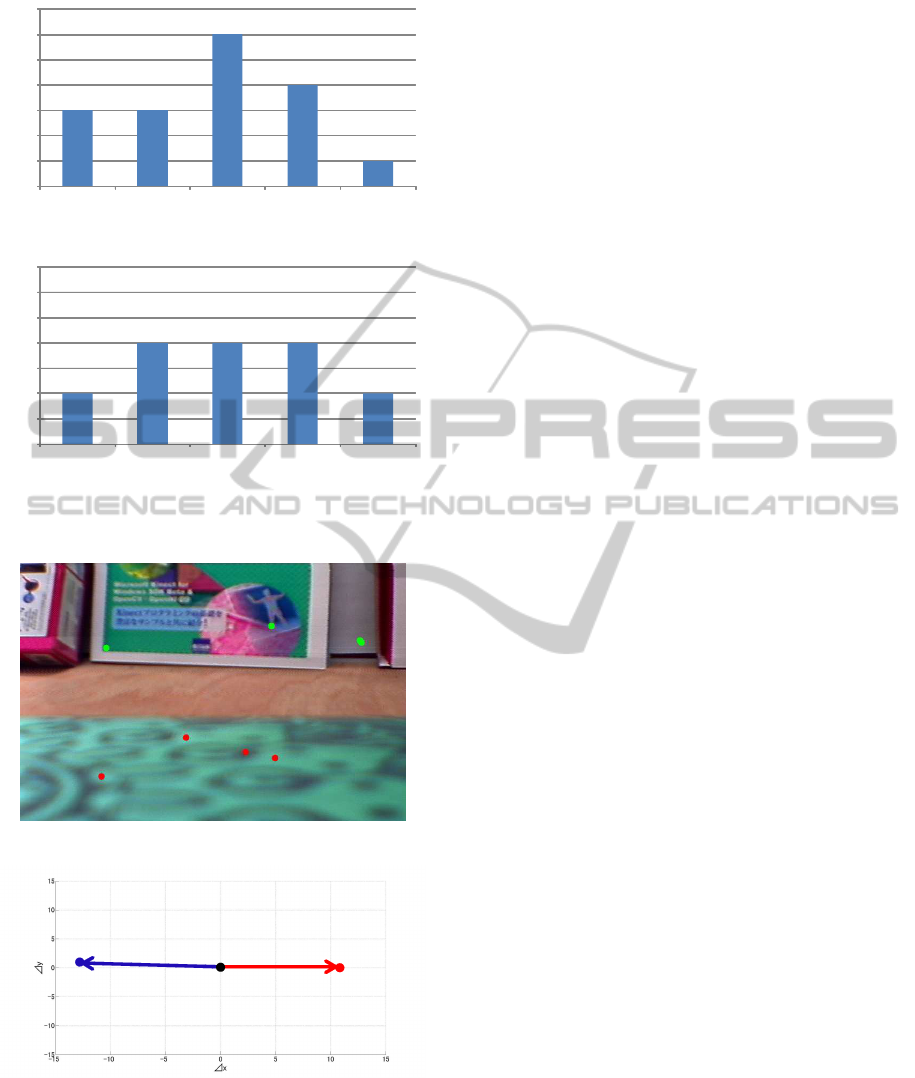
Ϭ
ϭ
Ϯ
ϯ
ϰ
ϱ
ϲ
ϳ
Ϭ͘ϭͲϬ͘Ϯ Ϭ͘ϮͲϬ͘ϯ Ϭ͘ϯͲϬ͘ϰ Ϭ͘ϰͲϬ͘ϱ Ϭ͘ϱͲϬ͘ϲ
Nnumber
Correlation coefficient
(a) Correlation coefficients of keypoints on the object.
Ϭ
ϭ
Ϯ
ϯ
ϰ
ϱ
ϲ
ϳ
Ϭ͘ϬͲϬ͘ϭ Ϭ͘ϭͲϬ͘Ϯ Ϭ͘ϮͲϬ͘ϯ Ϭ͘ϯͲϬ͘ϰ Ϭ͘ϰͲϬ͘ϱ
Number
Correlation coefficient
(b) Correlation coefficients of keypoints on background.
Figure 9: Histogram of correlation coefficient.
Figure 10: High and low correlation coefficient keypoint.
Figure 11: Estimated feature point motion.
5 CONCLUSIONS
In this paper, we proposed a method of extracting im-
age features whose positions are influential to their
dynamics. The proposed method is based on a sim-
ple motion of pushing and will be useful for higher-
level motion generation. In experiment, it was veri-
fied that the proposed method showed possibility to
extract useful image features for prediction of mo-
tions in the image. Distributions of motions of key-
points will be further investigated so as to realize bet-
ter variance approximation.
ACKNOWLEDGEMENTS
This research was partly supported by Research Foun-
dation for the Electro technology of Chubu.
REFERENCES
Asada, M., Hosoda, K., Kuniyoshi, Y., and Ishiguro, H.
(2009). Cognitive developmental robotics. Au-
tonomous Mental Development, IEEE Transactions
on, 1:2–341.
Comaniciu, D., Meer, P., and Member, IEEE, S. M. I.
(2002). Mean shift: A robust approach toward feature
space analysis. IEEE transactions on pattern analysis
and machine intelligence, 24(5):603–619.
Lowe, D. G. (2004). Distinctive image features from scale
invariant keypoints. International Journal of Com-
puter Vision, 60(2):91–110.
LLazaro-Gredilla, M. and Titsias, M. (2011). Variational
heteroscedastic gaussian process regression. Interna-
tional Conference on Machine Learning.
Madokoro, H., Utsumi, Y., and Sato, K. (2012). Scene
classication using unsupervised neural networks for
mobile robot vision. Society of Instrument and Con-
trol Engineers (SICE) Annual Conference 2012, pages
1568–1573.
McLachlan, G. and Krishnan, T. (2008). The EM Algorithm
and Extensions, 2nd Edition. WILEY.
Metta, G. and Fitzpatrick, P. (2003). Early integration of
vision and manipulation. Neural Networks, 2003. In-
ternational Joint Conference on, 4:2703–vol.
Moody, J. and Darken, C. J. (1989). Fast learning in net-
works of locallytuned processing units. Neural Com-
putation, 1(2):281–294.
Nakamura, T., Nagai, T., and Iwahashi, N. (2007). Mul-
timodal object categorization by a robot. Intelligent
Robots and Systems, 2007. IEEE/RSJ International
Conference on, pages 2415–2420.
Nishide, S., Ogata, T., Yokoya, R., Tani, J., Komatani, K.,
and Okuno, H. G. (2008). Object dyamics prediction
and motion generation based on reliable predictability.
Robotics and Automation. IEEE International Confer-
ence on, pages 1608–1614.
Rasmussen, C. and Williams, C. (2006). Gaussian Pro-
cesses for Machine Learning. The MIT Press.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement Learn-
ing: An Introduction. The MIT Press.
ExtractionofDynamics-correlatedFactorsfromImageFeaturesinPushingMotionofaMobileRobot
315
