Characterizing Generalization Algorithms

First Guidelines for Data Publishers

Feten Ben Fredj

1,2

, Nadira Lammari

and Isabelle Comyn-Wattiau

1,3

CEDRIC-CNAM, 292 rue Saint Martin, 75141, Paris Cedex 03, France

MIRACLE, Pôle technologique de Sfax, Route de Tunis Km 10 B.P. 242 Sfax 3021, Tunisia

ESSEC Business School, 1 Av B. Hirsch, 95000 Cergy, France

Keywords: Anonymization, Privacy, Generalization Technique, K-Anonymity, Algorithm, Guidelines.

Abstract: Many techniques, such as generalization algorithms have been proposed to ensure data anonymization

before publishing. However, data publishers may feel unable to choose the best algorithm given their

specific context. In this position paper, we describe synthetically the main generalization algorithms

focusing on their constraints and their advantages. Then we discuss the main criteria that can be used to

choose the best algorithm given a context. Two use cases are proposed, illustrating guidelines to help data

holders choosing an algorithm. Thus we contribute to knowledge management in the field of anonymization

algorithms. The approach can be applied to select an algorithm among other anonymization techniques

(micro-aggregation, swapping, etc.) and even first to select a technique.

1 INTRODUCTION

The volume of sensitive and/or confidential data

(salary, medical information, religious affiliation

may be considered as sensitive data) contained in

information systems becomes very important. In

many cases nowadays, we have to share such data.

Moreover, organizations, either public or private, are

more and more required to make publicly available

their data.

In order to ensure data anonymization,

companies remove personal identifiers, such as

social security numbers, first names and last names.

However, even without direct identification, these

data may be linked to external files and thus re-

identified. (Samarati, 2001) illustrates this risk,

using an example of medical records linked to an

electoral roll, using common attributes such as zip

code, birth date and sex.

Companies may implement specific techniques

to protect their data from disclosure risk. Most of

them are known as privacy preserving data

publishing (PPDP) techniques (Kiran and Kavya,

2012). Some of them are also privacy preserving

data mining (PPDM) techniques (Nayak and Devi,

2011). To the best of our knowledge, the most

familiar techniques for microdata anonymization

are: (1) data swapping which switches the values of

one attribute throughout the lines of a table

(Fienberg and McIntyre, 2004), (2) adding noise

(Brand, 2002) that consists in adding a random value

with a given distribution to all microdata, (3) micro-

aggregation (Defays and Nanopoulos, 1993) that

merges individual records into groups containing at

least k rows. Each merged record contains the means

of original individual values. Finally, generalization

(Samarati, 2001) replaces effective values with more

general ones (a date is truncated into a month, a city

is generalized into its related region, etc.).

Let us note that all anonymization techniques

aim not only to ensure data privacy but also to

preserve data usefulness. The latter is usually

measured using two kinds of metrics: data metrics

and search metrics (Fung et al., 2010). Data metrics

measure the difference between the quality of

original data and the quality of anonymized data.

Search metrics are used by algorithms to decide, at

each step, among several anonymization

transformations, the best one, i.e. minimizing data

distortion.

Each technique led to implementation of many

algorithms. Our preliminary state of the art allows us

to conclude that each algorithm presents some

advantages but also drawbacks and may be limited

to a specific context. We are convinced that

choosing the relevant technique and the best

360

Ben Fredj F., Lammari N. and Comyn-Wattiau I..

Characterizing Generalization Algorithms - First Guidelines for Data Publishers.

DOI: 10.5220/0005154603600366

In Proceedings of the International Conference on Knowledge Management and Information Sharing (KMIS-2014), pages 360-366

ISBN: 978-989-758-050-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

algorithm requires taking into account several

context parameters. Therefore, we have performed a

deep analysis of several generalization algorithms in

order to elicit such parameters. The research

question addressed in this paper is the following:

“based on literature, how can we provide data

holders with the knowledge about relevant

parameters helping them to select an adequate

generalization algorithm?”

The paper is organized as follows. Section 2

introduces the preliminary concepts allowing us to

describe generalization algorithms. In Section 3, we

describe the main generalization algorithms. Section

4 proposes a comparison table synthesizing the

different algorithms and finally, we conclude our

analysis and present future research.

2 PRELIMINARIES

Microdata are usually stored in relational tables

containing tuples representing individuals. Each

tuple has a value (microdata) for each attribute. The

latter can be an explicit identifier, a quasi-identifier,

a sensitive attribute or a non-sensitive one. An

Explicit Identifier (EI) directly identifies an

individual (e.g. social security number, first name,

last name). A Quasi-Identifier (QI) is a set of

attributes which, when linked to external

information, enables the re-identification of

individuals whose identifiers were removed. For

example (sex, zip code, and birthdate) is a well-

known quasi-identifier in many data sets. A

Sensitive Attribute (SA) represents data that

individuals don’t want to divulgate, such as medical

information or salaries. Non-Sensitive Attributes

(NSA) are attributes that are not included in previous

categories. For instance, in Table 1 representing the

original data set to be anonymized, the attributes

“age” and “education” constitute the QI. The

attribute “Disease” is a sensitive attribute (SA).

Table 1: Original data.

Explicit

Identifier

Quasi Identifier Sensitive

attribute

Name Age Education Disease

Alice 19 10th Diabetes

Jean 19 9th Cancer

Ines 27 9th Flu

David 30 9th Flu

Bob 23 11th Cancer

Dupont 23 11th Cancer

The generalization technique can be applied on a

continuous or a categorical attribute. A continuous

attribute is numerical and may take an infinite

number of different real values (e.g. the attribute

“age” in Table 1). A categorical attribute takes a

value in a limited set and arithmetic operations on it

do not make sense (e.g. the attribute “education” in

Table 1).

To avoid possible re-identification of individuals,

several privacy models have been proposed: k-

anonymity (Sweeney, 2002), l-diversity

(Machanavajjhala et al., 2007), t-closeness (Li, Li

and Venkatasubramanian, 2007), etc. In this paper,

we focus on k-anonymity since all generalization

algorithms are based on this privacy model. Let k be

an integer. An anonymized table satisfies k-

anonymity if each release of data is such that every

combination of values of quasi-identifiers can be

indistinctly matched to at least k individuals

(Sweeney, 2002). As an example, Table 2 is a

generalization of Table 1, satisfying 2-anonymity.

3 SOME GENERALIZATION

ALGORITHMS

Generalization technique consists in replacing data

values with more general ones (Samarati, 2001).

Therefore, data are true but less precise. The

generalization is applied on a quasi-identifier. It

requires the definition of a hierarchy for each

attribute of the QI. Each hierarchy contains at least

two levels. The root is the most general value. It

represents the highest level. The leaves correspond

to the original data values and constitute the lowest

level denoted 0. As an example, the tree at Figure 1a

represents a generalization hierarchy of the attribute

“education”. The node “Junior” is at the level 1 of

the hierarchy. Figure 1b is an example of hierarchy

for the attribute “age” where the latter is generalized

through intervals.

Figure 1: Generalization hierarchies for education and age.

The generalization technique is implemented thanks

to several different algorithms. The main ones are

described in the following paragraphs.

Secondary

Senior Junior

9th 10th 11th 12th

[19, 30]

[19, 23] [27, 30]

19 23 27 30

(a) (b)

CharacterizingGeneralizationAlgorithms-FirstGuidelinesforDataPublishers

361

Table 2: Generalized data.

Age Education Disease

[19,23] Junior Diabetes

[19,23] Junior Cancer

[27,30] Junior Flu

[19,23] Senior Cancer

3.1 μ-argus

μ-argus (Hundepool and Willenborg, 1996) is an

iterative algorithm. At each iteration (a) the data

holder chooses the attribute to be generalized, (b) the

algorithm replaces each value of this attribute with

the value of its direct parent in the corresponding

hierarchy, (c) it verifies the compliance of the

resulting table with the k-anonymity, and finally (d)

lets the data holder choose between suppressing

some values (i.e. replacing them with null values) in

the tuples that not satisfy the k-anonymity or

continuing the generalization process.

3.2 Datafly

Datafly (Sweeney, 1998) was the first algorithm able

to meet the k-anonymity requirement for a big set of

real data. In addition to the definition of k, it needs

the determination of the number of allowed tuple

suppressions (MaxSup). To minimize information

loss, at each iteration, DataFly (a) generalizes the

attributes having the highest number of distinct

values, (b) checks whether the resulting table

complies with the k-anonymity. If the number of

tuples which do not satisfy k-anonymity is lower

than MaxSup, then these tuples are removed and the

algorithm stops. Otherwise, the algorithm performs

another iteration of generalization. Thus, combining

generalization and suppression prevents from an

excessive generalization which would reduce data

usefulness.

3.3 Samarati’s Algorithm

Samarati’s algorithm (Samarati, 2001) is based on a

lattice representing the possible combinations of

generalization levels. Each node, in the lattice,

contains a list describing the generalization level of

each QI attribute (Fig. 2). Thus, each node

corresponds to a possible anonymization (genera-

lization) of the original table. For example, starting

from Table 1, the implementation of <A1,E1> leads

to Table 2. All the values of the attribute “age”

which are of level 0 in Table 1 will be replaced with

their parents of level 1 in the Table 2. The same

transformation is performed for the values of the

attribute “education”.

Figure 2: The generalization lattice of the two attributes

age and education.

Samarati argues that the best anonymization

results are the nodes satisfying k-anonymity,

potentially with suppression but limited to MaxSup

(number of tuple suppressions allowed) and located,

as much as possible, at the bottom of the lattice (that

means minimizing information loss). In order to find

these optimal nodes, the algorithm considers the

nodes at the level h/2, h being the height of the

unexplored part of the lattice (the whole lattice is

considered at the first iteration). As an illustration,

for the lattice at Figure 2, h is equal to 4. The nodes

located at h/2=2 are <A2,E0>, <A1,E1> and

<A0,E2>. Each iteration works as follows: if, at the

level h/2, at least one node satisfies k-anonymity, the

algorithm stores together all the nodes satisfying k-

anonymity. Then, it concentrates on the lower half

of the lattice and computes the new value of h/2. On

the contrary, if there is not any node satisfying k-

anonymity at this level, the algorithm targets the

upper half of the lattice. The algorithm stops when h

is equal to 0. The final result consists of the last

stored nodes.

3.4 Incognito

Incognito (LeFevre, DeWitt and Ramakrishnan,

2005) is also based on a lattice. However, the latter

is built iteratively in order to achieve more

efficiency. At each iteration i, it builds all possible

lattices of i attributes by joining lattices of (i-1)th

iteration (except for iteration 1 where lattices are

built using the generalization hierarchies). Then, in

the resulting lattices, it removes all the nodes not

compliant with k-anonymity. At the end of the

process, the resulting lattice contains all the possible

generalizations satisfying k-anonymity. The data

holder has then to choose one generalization among

those proposed in the lattice.

3.5 Bottom up Generalization

This algorithm has been proposed by (Wang et al.,

<A0, E0>

<A1, E0> <A0, E1>

<A2, E0><A1, E1><A0, E2>

<A2, E1> <A1, E2>

<A2, E2>

KMIS2014-InternationalConferenceonKnowledgeManagementandInformationSharing

362

2004) and is dedicated to a specific data mining task

which is the classification. Like most generalization

algorithms, Bottom Up algorithm builds the

anonymized table iteratively. At each step, the

algorithm selects, among the candidate

generalizations, the one that provides the data

publisher with more anonymity while best

preserving the quality of the classification. The

information loss regarding the classification and the

anonymity gain are measured using a metric. The

process is stopped when the table satisfies the k-

anonymity. A generalization (a node in the

generalization hierarchy) is considered as candidate

regarding a table if its children in the generalization

hierarchy are also in the table. For instance, the

value “secondary” is not a candidate generalization

for Table 1 since its children (“junior” and “senior”)

aren’t in this table.

3.6 Top down Specialization

Like Bottom Up generalization, Top Down

Specialization (commonly called TDS) (Fung, Wang

and Yu, 2005) is dedicated to classification.

However, TDS is a top-down approach since it

browses the generalization hierarchy from top to

bottom.

TDS assumes that a maximum generalization of

all the values of the original table will preserve k-

anonymity but can affect the quality of the resulting

table in terms of classification. Therefore it performs

iterations to find the best specializations i.e. those

that not only satisfy k-anonymity but also generate

less anonymity loss, thus enabling better quality

with respect to the classification.

3.7 Median Mondrian

The principle of Median Mondrian (LeFevre et al.,

2006a) is to divide the set of individuals (tuples)

represented in the table into groups such that each

group contains at least k individuals (to satisfy k-

anonymity). Then, the individuals which belong to

the same group will have the same value for their QI

via the generalization process. More precisely,

individuals (tuples of the original table) are

represented, thanks to the values of their QI, in a

multidimensional space where each dimension

corresponds to an attribute of the QI (Fig. 3). The

splitting of the space into areas corresponds to the

constitution of groups of individuals. It is performed

using the median.

At each iteration, the algorithm chooses a

dimension and checks the possibility of splitting a

group into two groups (splitting the area on the

median value of this dimension). A group can be

divided into two groups if in each resulting group

there are at least k individuals (k-anonymity

condition). Every group for which the division is not

allowed is marked. The splitting process switches to

another dimension when all groups are marked for

the current dimension. It stops when all dimensions

have been explored. Then the algorithm performs

the proposed generalizations, replacing the different

values in the same area with the value of their first

common parent (recoding process).

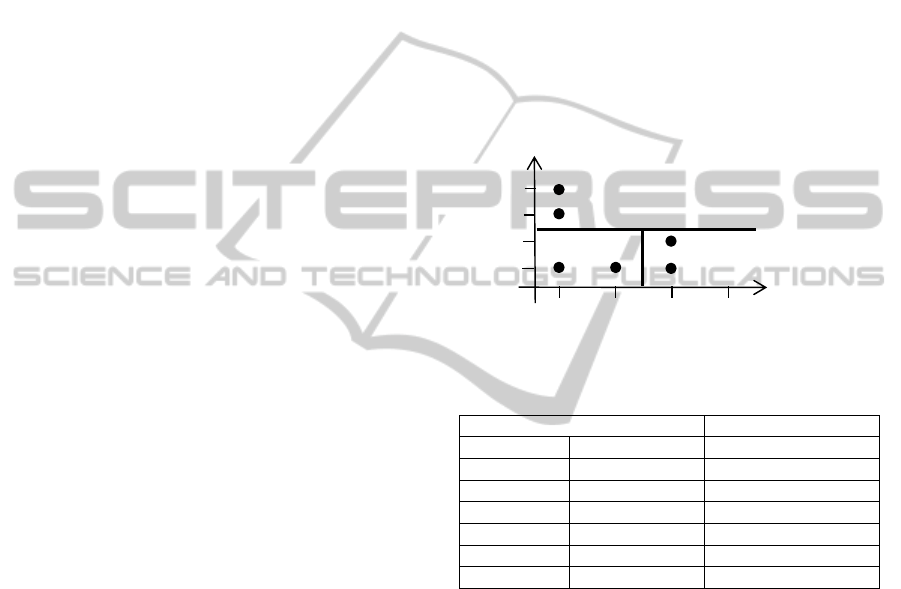
Figure 3 shows the result of the splitting process

performed on Table 1 that satisfies 2-anonymity.

Table 3 is the anonymized table generated from the

recoding proposed at Fig. 3.

Figure 3: 2-dimensional space for age and education

Table 3: Recoding of Figure 3

Quasi identifier attributes Sensitive attribute

Age Education Disease

19 Junior Diabetes

19 Junior Cancer

[27,30] 9

Flu

[27,30] 9

Flu

23 11

Cancer

23 11

Cancer

3.8 InfoGain Mondrian and LSD

Mondrian

These two algorithms extend the previous one

(Median Mondrian) (LeFevre et al., 2006a). In their

splitting process, they use a metric that permits to

choose, among a set of allowed divisions, the best

division i.e. that preserves either the classification

(Infogain Mondrian) or the regression (LSD

Mondrian).

4 DISCUSSION

An extensive attention has been paid to privacy

protection by statistics and computer science

communities during past years. A large body of

9th 10th 11th 12th

Area 1

Area 2

Division

Education

Age

rea 3

CharacterizingGeneralizationAlgorithms-FirstGuidelinesforDataPublishers

363

research works has brought techniques and

algorithms trying to ensure the non-re-identification

of sensitive information while maintaining

usefulness of these data. However, we noticed the

lack of approaches guiding data holders in the

choice of techniques and, given a technique, of an

algorithm among all existing implementations of this

technique. Thus, we conducted a detailed review,

dedicated to generalization techniques, aiming to

elicit first guidelines helping data publishers to

choose a generalization algorithm. We have

compared the algorithms according their four

constituents: pre-requisites, inputs, process and

outputs (Table 4). Some algorithms, such as

Incognito and Samarati, are restricted to small data

sets (Fung et al., 2010). All of them are limited to

categorical and continuous micro data. Moreover,

algorithms preserving the classification or regression

capabilities require correlation between multiple

target attributes (LeFevre, DeWitt and

Ramakrishnan, 2006b).

All generalization algorithms require input

parameters. At least we need to decide the value of k

(corresponding to k-anonymity), to declare which

columns constitute the QI and finally we have to

provide the generalization hierarchies. Let us note

that some algorithms can compute the generalization

hierarchy for continuous attributes. Moreover, for

algorithms including tuple suppressions, the number

of allowed suppressions (MaxSup) is also an input

parameter. Finally, all the algorithms that preserve

the quality of data regarding a data mining specific

task such as classification or regression require the

declaration of at least one target attribute.

From process point of view, we can notice that

some algorithms are completely automatic. Most of

them are iterative processes guided (Sweeney, 1998)

or not (Samarati, 2001) by metrics. Moreover, some

of them are bottom up processes (Sweeney, 1998)

where small groups of tuples are constituted and

then merged iteratively until each group contains at

least k rows (k-anonymity satisfaction) (Fung et al.,

2010). The other ones are top down processes (Fung,

Wang and Yu, 2005) i.e. they start from a group

containing all rows and iteratively split each group

into two subgroups while preserving k-anonymity.

Finally, the generalization algorithms do not all

provide the same outputs. Some algorithms deliver a

unique anonymized table while others compute

several alternative tables. Some algorithms compute

an optimal k-anonymity solution but they are limited

to small data sets (Fung et al., 2010). Others, based

on heuristics, do not guarantee the optimality.

Finally, they may provide three different

generalizations that we define as: full-domain, sub-

tree and multidimensional generalization. Full-

domain means that, for a given generalized column,

all the values in the output table belong to the same

level of the generalization hierarchy. Sub-tree means

that values sharing the same direct parent in the

hierarchy are necessarily generalized at the same

level, taking the value of one of their common

ancestors. Finally, in multidimensional

generalizations, two identical values in the original

table may lead to different generalized values (i.e.

are not generalized at the same level).

In terms of usage scenario, let us note that the

data resulting from anonymization are designed for

specific usages. Bottom up generalization, top down

specialization and InfoGain Mondrian produce data

for classification tasks. LSD Mondrian is used in the

case where regression will be performed on the

anonymized data.

Our comparative study helps us to define

patterns that capture knowledge about the main

generalization algorithms. These patterns will be

part of a knowledge base. The latter will be made

available through a guidance approach to help data

publishers in the choice of the anonymization

algorithms. We are convinced that the guidance

depends on the data publisher expertise level. We

expect several expertise levels and, for each level, at

least one guidance scenario. A guidance scenario

consists of a list of generalization algorithms (at

least one) according to the context. These context

elements are linked to the set of criteria used in our

comparative study. For instance, the size of a data

set to be anonymized and the usage scenario are the

two parameters that we consider relevant for the

definition of guidance scenarios addressed to data

publishers who don’t have technical skills in

anonymization. An example of scenario follows:

“If you don’t project a specific usage of your

large data set then you can perform Datafly, µ-argus

or Median Mondrian”.

For a data publisher having a little expertise in

anonymization, a guidance scenario could be: “If

you don’t project a specific usage of your small data

set and if you wish to have an anonymized data set

satisfying an optimal k-anonymity

and having all the

values of each anonymized attribute at the same

level of the generalization hierarchy (full-domain

generalization) then you can perform Samarati or

Incognito”. In this scenario the criteria used to select

the algorithms are respectively: “Scenario of usage”,

“Size of dataset”, “Quality”, and “Generalization

type”.

KMIS2014-InternationalConferenceonKnowledgeManagementandInformationSharing

364

Table 4: Comparison of generalization algorithms.

5 CONCLUSIONS

Many similar surveys have been proposed in the

literature. Some of them are usage-oriented

(Ilavarasi et al., 2013; Nayak and Devi, 2011; Singh

and Parihar, 2013; Fung et al. 2010, etc.). They

usually analyze different anonymization techniques

highlighting their advantages and drawbacks and

propose research directions. Others are technique-

oriented (Patel and Gupta, 2013; Sharma, 2012; Xu

et al., 2014). To our knowledge, only (Xu et al.,

2014) and (Kiran and Kavya, 2012) are close to our

research since they focus on the generalisation

technique and its related algorithms. However they

differ from our work regarding the objectives they

serve. (Kiran and Kavya, 2012), after a detailed

description of some generalization algorithms,

focuses on data quality through metrics analysis.

(Xu et al., 2014) proposes profiles describing some

generalization algorithms for researchers wishing to

work on data anonymization.

Our comparison allowed us to derive guidelines

for data publishers helping them to choose an

algorithm given a context. The first answer to our

research question is to propose guidelines as a first

formalization of knowledge on anonymization

algorithms. Through our extensive literature study,

we found out that such guidelines must be different

depending on the expertise level of data publishers.

This is a research in progress. Starting from this

comparison, we are now defining patterns describing

these algorithms. Each pattern will contain the main

characteristics of algorithms, the use cases, an

application example, the alternative algorithms, etc.

The final objective is to propose a whole approach

characterizing the data and the context, deducing the

relevant technique and the appropriate algorithm,

and finally performing the anonymization process.

REFERENCES

Brand, R, 2002. Microdata protection through noise

addition. In Domingo-Ferrer J, editor, Inference

Control in Statistical Databases, Vol. 2316 of LNCS,

pp 97-116, Springer Berlin Heidelberg.

Defays, D and Nanopoulos, P, 1993. Panels of enterprises

and confidentiality: the small aggregates method. In

Proc. 92nd Symposium on Design and Analysis of

Longitudinal Surveys, pp 195-204, Statistics Canada.

Fienberg, SE, McIntyre, J., 2004. Data Swapping:

Variations on a Theme by Dalenius and Reiss, In J.

Domingo-Ferrer and V. Torra (Eds.): PSD 2004,

LNCS 3050, pp. 14–29, Springer Berlin Heidelberg.

Fung, BCM, Wang, K, Yu, PS, 2005. Top-down

specialization for information and privacy

preservation. In Proc. 21st IEEE Intl Conference on

Data Engineering (ICDE). pp. 205–216.

Fung, BCM, Wang, K, Chen, R and Yu PS, 2010. Privacy-

Preserving Data Publishing: A Survey of Recent

Developments. ACM Computing Surveys, Vol. 42, No.

4, Article 14

Hundepool, A and Willenborg, L, 1996. µ - and τ-argus:

Software for statistical disclosure control. In Proc 3rd

Intl Seminar on Statistical Confidentiality, Bled.

Ilavarasi, AK, Sathiyabhama, B and Poorani, S., 2013. A

Survey on Privacy Preserving Data Mining

Samarati Incognito Datafly µ-Argus

Bottom up

Generalization

Top Down

Specialization

Median

Mondr ian

InfoGain

Mondr ian

LSD

Mondrian

Limited to small data

set

At least 2 attributes

are correlated

HCO **

MaxSu

Yes NA Yes

Tar

et attributes

Automation Degree

Semi-automatic

Guided b

metrics

Heuristic process

Bottom up/Top down

Multi

licit

Qualit

Generalisation type

Scenario of usage

Any

scenario

Classification Regression

** HCO represents the set of generalization hierarchies for continuous attributes (one per attribute)

Automatic

optimal k-anonymity not necessarily an optimal k-anonymity

Full-domain MultidimensionalSub-tree

Yes

YesNo

Yes No

NA one at least one

Automatic

Additional

inputs

Process

Bottom up Top down

Pre-

requisites

Verified

Yes

At least one table Only one output table

* NA means not applicable

Outputs

ClassificationAny scenario

CharacterizingGeneralizationAlgorithms-FirstGuidelinesforDataPublishers

365

Techniques. In International Journal of Computer

Science and Business Informatics. Vol 7, No 1.

Kiran, P and Kavya, NP, 2012. A Survey on Methods,

Attacks and Metric for Privacy Preserving Data

Publishing. In International Journal of Computer

Applications, Vol 53, No 18.

LeFevre, K, DeWitt, DJ and Ramakrishnan, R, 2005.

Incognito: Efficient full-domain k-anonymity. In Proc.

ACM Intl Conf on Management of data (SIGMOD).

LeFevre, K, DeWitt, DJ and Ramakrishnan, R, 2006a.

Mondrian multidimensional k-anonymity. In Proc

22nd IEEE Intl Conference on Data Engineering

(ICDE).

LeFevre, K, DeWitt, DJ, Ramakrishnan, R, R., 2006b.

Workload-aware anonymization. In Proc 12th ACM

SIGKDD Intl Conf on Knowledge discovery and data

mining.

Li, N, Li, T and Venkatasubramanian, S, 2007. t-

closeness: Privacy beyond k-anonymity and l-

diversity. In Proc 21st IEEE International Conference

on Data Engineering (ICDE).

Machanavajjhala, A, Gehrke, J, Kifer, D and

Venkitasubramaniam, M, 2007. l-diversity: Privacy

beyond k-anonymity. In Proc. 22nd IEEE Intl Conf on

Data Engineering (ICDE).

Nayak, G, Devi, S, 2011. A General Survey of Privacy-

Preserving Data Mining Models and Algorithms. In

International Journal of Engineering Science and

Technology (IJEST), Vol 3, No 3.

Patel, L and Gupta, R, 2013. A Survey of Perturbation

Technique For Privacy-Preserving of Data. In

International Journal of Emerging Technology and

Advanced Engineering, Vol 3, N° 6.

Samarati, P. 2001. Protecting respondents’ identities in

microdata release. IEEE Transactions on Knowledge

and Data Engineering, Vol 13, N°6.

Sharma, D, 2012. A Survey on Maintaining Privacy in

Data Mining. In International Journal Of Engineering

Research And Technology Vol. 1, N°2.

Singh AP and Parihar D, 2013. A review of privacy

preserving data publishing technique. In International

Journal of Emerging Research in Management

andTechnology Vol. 2, N°6.

Sweeney, L. 1998. Datafly: A system for providing

anonymity in medical data. In: Proceedings of the

IFIP TC11 WG11.3 Eleventh International

Conference on Database Security XI: Status and

Prospects, Pages 356-381, Chapman and Hall, Ltd.

Sweeney, L. 2002. k-Anonymity: A model for protecting

privacy. Intl Journal of Uncertainty, Fuzziness and

Knowledge-Based Systems, Vol. 10, N°5.

Wang, K, Yu, P and Chakraborty, S. 2004. Bottom-up

generalization: A data mining solution to privacy

protection. In Proc. 4th IEEE Intl Conf on Data

Mining (ICDM).

Xu Y, Ma T, Tang M and Tian W, 2014. A survey of

privacy preserving data publishing using

generalization and suppression. In International

Journal Applied Mathematics and Information

Sciences, Vol 8, N°3.

KMIS2014-InternationalConferenceonKnowledgeManagementandInformationSharing

366