A Variable Neighborhood Search for Solving Sudoku Puzzles
Khorshid Adel Hamza and Aise Zulal Sevkli
Fatih University, Department of Computer Engineering, 34500 Buyukcekmece, Istanbul, Turkiye
Keywords: Sudoku Puzzles, Variable Neighbourhood Search, Neighbourhood Structures, Metaheuristics.
Abstract: Sudoku is a well-known puzzle that has achieved international popularity in the latest decade. Recently,
there are explosive growths in the application of metaheuristic algorithms for solving Sudoku puzzles. In
this paper, an algorithm based on Variable Neighborhood Search (VNS) is proposed to solve the Sudoku
problem and the details of the implementation such as problem representation, neighbourhood structures are
explained. The proposed algorithm is tested with Sudoku benchmarks which have been used in previous
studies. The experimental results indicate that VNS is able to produce competitive results in easy level
puzzles and promising results in medium and hard level puzzles.
1 INTRODUCTION
The Sudoku game is one of the most interesting
challenging games which have been well known
around the world. It is spread through different kinds
of media, from newspapers to internet sites as well
as mobile applications. Beside the popularity of the
game, Sudoku is known as a NP-complete problem
(Yato and Seta, 2003); these factors attract many
researchers to apply different metaheuristics
algorithms to solve Sudoku puzzles. The difference
between researcher’s results lies in their algorithms’
abilities to reach Sudoku optimal solution in
reasonable time, so the rate of success and the
number of iterations and elapsed times are the most
important factors in comparing their performance.
First, we will shed lights on previous researches
which submitted for solving Sudoku game; we found
that most of these implementations use population-
based metaheuristics such as Genetic algorithm
(GA) , Harmony Algorithm (HA), Ant Colony
Optimization (ACO) etc. On the other hand, there
are a few trajectory-based metaheuristic
implementations in this field, the earlier one was
used Simulated Annealing in 2006. In this paper we
proposed a trajectory-based VNS algorithm to solve
different levels of Sudoku problem and tested our
algorithm with the benchmarks that used in the
previous studies.
2 SUDOKU GAME
Sudoku has been claimed to be very popular and
even addictive because it’s easy to play as it doesn’t
require general knowledge, linguistic ability or even
mathematical skills, with simple rules but very
challenging game with different levels.
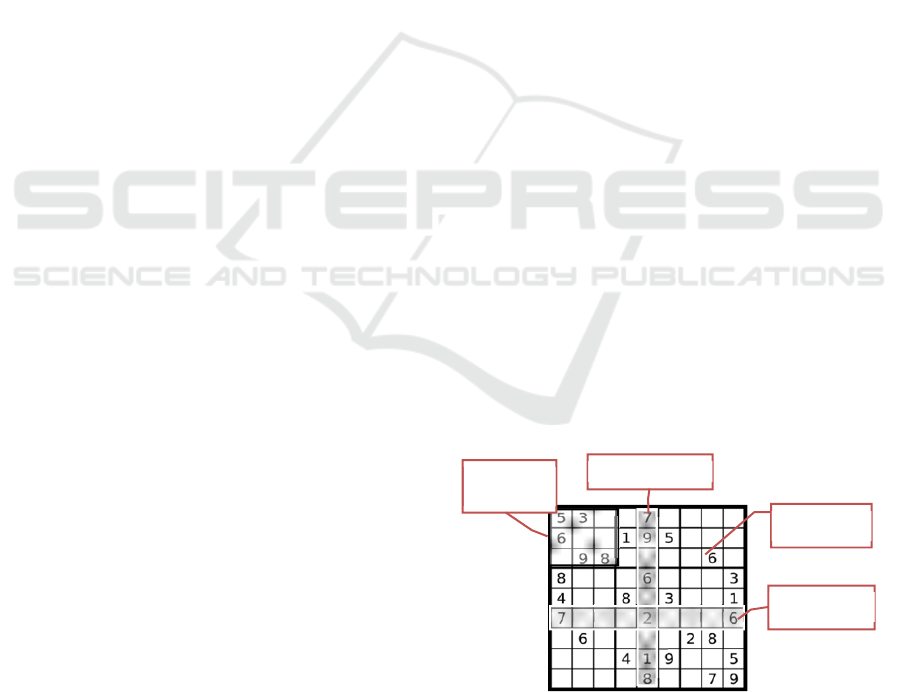
Figure 1: A Sample of Sudoku puzzle.
Sudoku puzzle with order 9×9 are composed of a
9 × 9
boxes (cells) namely of 81 positions as shown
in Figure 1, they divided into nine 3×3 sub-blocks.
When the Sudoku game is prepared to play, there are
some pre-filled (fixed) numbers which are not
allowed to changed or moved during the process of
solving Sudoku puzzles, then you will start to fill
other unfilled boxes (unfixed) in such way so that
each row, column and 3×3 sub-blocks contain each
integer {1,2,3,4,5,6,7,8,9} once and only once.
Filling all the cells in Sudoku will be the solution.
Finally, in solving Sudoku puzzles, we deal with
FixedCell
Row
Column
Sub‐
block
326
Hamza K. and Sevkli A..
A Variable Neighborhood Search for Solving Sudoku Puzzles.
DOI: 10.5220/0005154903260331
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 326-331
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

puzzles that have unique solution. We can
summarize rules to solve Sudoku into three rules
(Satyendra and Saumi, 2013):
- Rule 1: Each row should contain values from 1 to 9
without repeating any number.
- Rule 2: Each column should contain values from 1
to 9 without repeating any number.
- Rule 3: The sub-block should contain only values
from 1 to 9 without repetition.
3 RELATED WORK
Many algorithms were proposed for solving and
generating Sudoku problems. A number of studies
can definitely solve Sudoku problems by using exact
methods (Crawford et.al, 2008), (Gunther and
Moon, 2012) and (Simonis, 2005). By using these
exact methods, easy level Sudoku problems can be
solved in a reasonable amount of time. However,
when the level gets harder, the computational time
grows exponentially and these methods become
impractical. Therefore, many researchers focus on
heuristic algorithms.
Various population-based metaheuristics have
been proposed such as ant colony optimization
algorithm (ACO) (Asif, 2009), genetic algorithm
(GA) (Xiuqin, Yongda and Ruichu, 2012), (Li and
Deng, 2011) and (Mantere and Koljonen, 2007),
harmony search algorithm (HS) (Satyendra and
Saumi, 2013). In the paper (Asif, 2009), the author
employs as heuristic information the number of
digits correctly placed on the board. However, the
best value reached is 76 where 81 being the global
optimum. Li and Deng (2011) proposed a modified
genetic algorithm for solving Sudoku games under
the name of Improved Genetic Algorithm. The
results were good in solving easy levels but it was
unable to solve higher levels. They followed their
algorithm with New Genetic algorithm (NGA)
(Xiuqin, Yongda and Ruichu, 2012) which contains
many major modifications. The results were
significantly improved in solving all Sudoku levels
even when comparing the results with other
population algorithms like GA (Mantere and
Koljonen, 2007), Cultural Algorithm (CA) (Mantere
and Koljonen, 2008) and ACO (Mantere and
Koljonen, 2009).
Another algorithm has been published by
Satyendra and Saumi (2013) using harmony
algorithm. The algorithm in addition to solving
different levels of Sudoku, it can determine the level
of the Sudoku game. The results were quite good in
solving easy levels with success rate of 100%, but
these rates are decreased along with levels of
difficulty to be 10% in the hardest level (level 5).
Although there are many population based
heuristic algorithms, there are a few trajectory-based
algorithms for solving Sudoku games. Lewis (2007)
proposed a simulated annealing algorithm to solve
different level types of (3 * 3) Sudoku games as well
as (4
* 4) games. In addition, he developed an
algorithm to create solvable problem instances with
different levels by using some rules and criteria. The
results were amazing as the algorithm solved all
samples of all levels in short time, but with more
times in solving 4 * 4 Sudoku problems. The main
factor of
reducing running time was in calculating
the fitness function by recalculating only affected
rows and columns by the swap neighborhood
structure operation. Unfortunately, the data set used
in experiments is unavailable to compare his results
with our results.
4 VNS IMPLEMENTATION
In this paper we propose a Variable Neighborhood
Search (VNS) algorithm to solve Sudoku problem.
Variable Neighborhood Search has been proposed
by Mladenovic and Hansen (1997). The basic idea of
VNS is to successively explore a set of predefined
neighborhoods to provide a better diversification of
solution. It explores either at random or
systematically a set of neighborhoods to get different
local optima and to escape from local optima. VNS
Figure 2: Pseudo-code of GVNS algorithm.
Input: a set of neighborhood structures N
k
for k = 1,,
k
max
for shaking.
a set of neighborhood structures N
l
for l = 1,.. l
max
for
local search.
x = x
0
;
Repeat
For k=1 to k
max
Do
Shaking: pick a random solution xʹ′from the k
th
neighborhood N
k
(x) of xʹ ;
Local search by VND ;
For j=1 To j
max
Do
Find the best neighbor x′′ of x′ in N
j
(x′) ;
If f (x′′) < f (x′) Then x′= x′′ ; j=1 ;
Otherwise j=j+1;
Move or not:
If local optimum is better than x Then x = xʺ
Continue to search with N
1
(k = 1) ;
Otherwise k=k+1 ;
Until stopping criteria
Output: Best found solution
AVariableNeighborhoodSearchforSolvingSudokuPuzzles
327
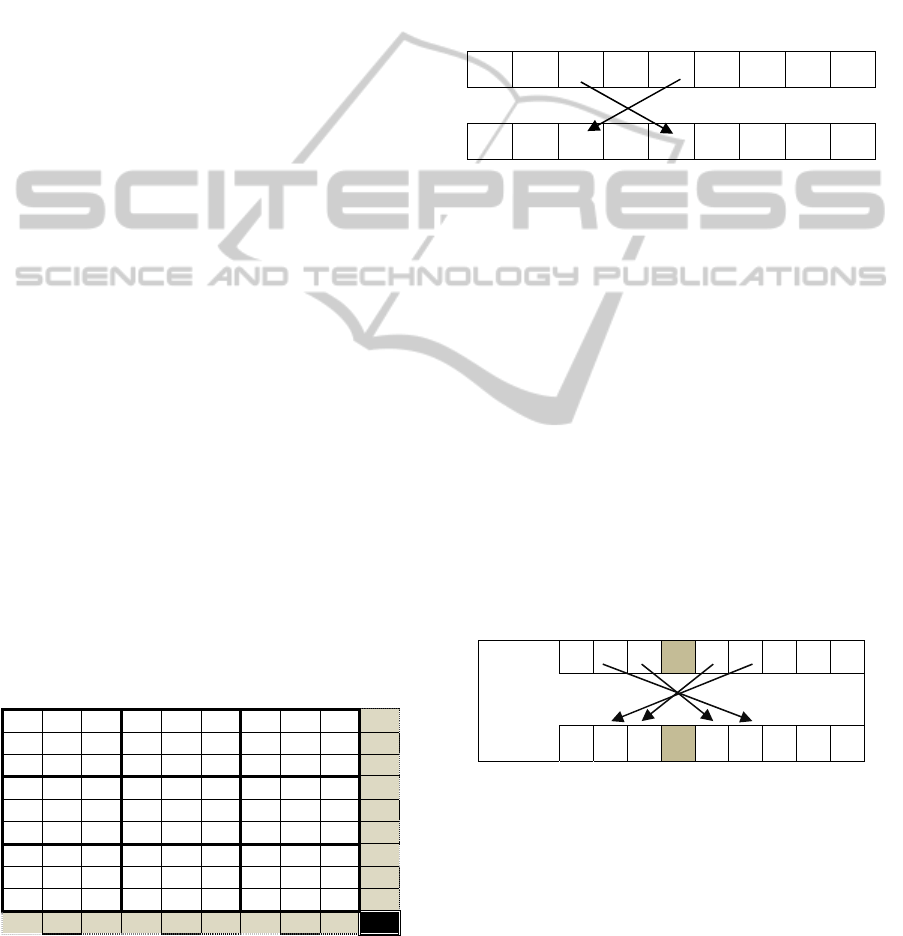
algorithm has three main phases: Shake, Local
Search and Move or Not. While shake diversifies the
solution, local search explores local area thoroughly.
Variable Neighborhood Descent (VND) is a
variation of the VNS. It explores local optima with
using various neighborhood structures only. VND
can be used as a part of VNS in the local search
phase which is called general VNS (GVNS).
In this study, a GVNS algorithm where the
simple local search procedure is replaced by the
VND algorithm is used. The pseudo-code of GVNS
algorithm is described in Figure 2.
4.1 The Fitness Function
The initial solution is created based on rule 3 which
keeps the numbers between 1 and 9 without
repeating in every sub-block. It’s clear that
appropriate fitness function is obviously one that
searches for violations of the remaining two rules
(rule 1 and 2). To calculate fitness value, repeating
number at each row and column are calculated. Total
of these numbers give the fitness value of the
candidate solution. Calculation of fitness value for a
sample Sudoku puzzle is given in Table 1.
Obviously, fitness value of an optimal solution is
zero. Note that to calculate the missed numbers in
row and column, we count number which are
repeated more than one; then it subtracted by 1. For
instance, if a number repeated two times in a row,
counter equals 2-1=1, if a number repeated three
times it will be 3-1=2 etc. this is because if 2
numbers repeated in row, it means that one numbers
is missed, and if we have three numbers then we
have 2 missed numbers. This calculation makes for
every the rows and columns. The total fitness will be
the summation of all rows and columns fitness as
showed in Table 1.
Table 1: Calculation of fitness of the sample Sudoku
puzzle
3
2 5
4 1
7
6 3
4
2
9 8
1
9 8
5
7
2
1 3
7
6 4 3
2
6
5
9 8 1
5
2 9 6 3
4 8
7 1 0
1 3 6 7 9 8 2 4 5 0
4 8
7 5
1 2 6 3
9
0
6 1
3
8
7
4 2 8
6
2
7
4
5
1
6 3
7
5 3 3
8
9 2
2
5 9
9 1
4 3
1 2 1 0 1 1 3 1 2
26
4.2 Neighbourhood Structures
The variety of neighborhood structures is an initial
condition to escape from local optima in order to
find the optimal solution. For this purpose, we
defined four neighborhood structures (NS).
Following sections describes each of them. While
the first three NS are used in VND local search
phase, the last one is used in shaking phase.
4.2.1 Exchange
In this structure, two non-fixed boxes in the same
sub-block selected randomly. Then they are simply
swapped as shown in Figure 3.
1
2 3 4 5 6 7
8
9
1
2 5 4 3 6 7
8
9
Figure 3: An example of exchange NS inside sub-block.
4.2.2 A Centered Point Oriented Exchange
(CPOEx)
This structure is used to explore new solutions in a
little further vicinity of a current solution. At first, a
box is selected randomly in a sub-block. NS is used
this box as a centered point to find exchange pairs.
Starting from the nearest boxes to the centered point,
exchange-pairs are determined and then applied
exchange NS. The CPOex continues to find
appropriate exchange-pairs until one or both boxes
of pair consisted of a fixed cell. A sample of CPOEx
is illustrated in Figure 4. The shaded box indicates a
centered point (cell 4) and bold numbers are fixed
(cell 1 and 8). In this example CPOEx are stands for
two exchange operations, but number of exchanges
depend on the location of the center point and fixed
cells in sub-block.
Before
1
2 3 4 5 6 7
8
9
After
1
6 5
4 3 2 7
8
9
Figure 4: Example of CPOEx with no changes in a sub-
block.
4.2.3 Insert
Another NS used in this study is inserting. This
structure performs an insertion of a box chosen
randomly from the sub-block, in front of another
randomly chosen box. An example of insert NS is
given in the Figure 5.
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
328

Start
Point
1
2 3 4 5 6 7
8
9
1
2 6
3 4 5 7
8
9
Insertion
Point
Figure 5: Insert NS operation.
First we choose a random number as start point,
(box 6), then we choose another random number as
inserting point (box 3). The procedure is done by
inserting the number in box (6) in front of the box
(3). This operation will shift right
hand numbers.
Notice that the fixed box (8) wasn’t affected by the
fixed cells. If insertion of a box is fixed, the insert
does not work. But the other box is fixed the
insertion could be done without affecting the places
of fixed boxes.
4.2.4 Invert
The last NS is used in the shaking phase of GVNS.
The idea is to select two boxes in the sub-block
randomly, then invert a subsequence of boxes
between two selected boxes. Both the boxes outside
the range and the fixed boxes in the range are not
affected by the invert operation. In figure 6, we
randomly select cell 3 and 6 which means we have
four boxes {3,4,5, 6}. The inverse of these values we
get {6, 5, 4, 3}
1
2
3 4 5 6 7
8
9
1
2 6 5 4 3 7
8
9
Figure 6: Invert NS operation.
4.3 The Procedure
The algorithm starts with a generating initial
solution x randomly but at the same time we should
satisfy the third rule which ensures that no values are
repeated inside sub-blocks. In the course of
following two nested loops, the algorithm explores
the solutions and tries to find the best solution. Local
search and Shake functions perform this exploration,
systematically. The function Shake updates the
solution x, with another solution x’, by applying
Invert NS to some sub-blocks of the problem.
NSs are usually ranked in such a way that VNS
algorithm explores increasingly further away from
the incumbent solution. In our proposed algorithm,
we ordered NSs in local search phase as follows:
exchange, insert, and CPOEx. The tests also showed
that these order are more efficient than other orders.
The result of Shake, x’, is used as the starting point
for the local search. Starting from the first sub-
block, all variations of exchange pairs are
experimented. If the best solution of exchange NS xʺ
better than x’, the local search starts all over again
from exchange NS. Otherwise, local search
continues from next neighborhood structure. This
local search loop is terminated after all
neighborhood structures are exhausted. If the best
solution of local search xʺ better than x , algorithm
starts all over again from Shaking phase with xʺ
otherwise with x. This procedure goes on until
stopping condition is met. Possible stopping
conditions include maximum CPU time allowed,
maximum number of iterations or maximum number
of iterations between two improvements.
5 EXPERIMENTAL RESULTS
To test our VNS implementation with Sudoku
games, we choose 15 benchmark of Sudoku samples
(
http://lipas.uwasa.fi/~timan/sudoku/) which has been
used in testing GA based algorithm (Xiuqin et al.,
2012). The experiments are done 10 times for every
game sample with maximum iterations 10000. The
experimentation has been carried out on a PC
equipped with Intel(R) Core (TM) i3 2.53 GHz
processor and 4GB memory. The software coded in
Visual C#. The results are shown in Table 2.
We choose first five problem sets which
numbered from 1 to 5. Level 1 stand for easier level
and level 5 for the most difficult level. Each level
has three instances labeled as (a, b and c). From the
Table 2, results show that our VNS experiments with
maximum 10000 iterations can solve easy level
problems (level 1) including all three instances (a, b
and c) with high success ratio (100%, 90 and 80%)
respectively. This is a high rate of success exactly as
we expect. Also the time to solve this level is
acceptable except c instance which takes average
time more than others. The success rate is still high
in level 2 which is more difficult than level 1. The
iterations needed to solve level 2 become larger and
this increases the time as well. Level 3 can only
solve type (a) in high success rate. Other b and c can
be solved only 2 times out of 10 (20%). Level 5
which is the difficult level is a serious challenge to
AVariableNeighborhoodSearchforSolvingSudokuPuzzles
329
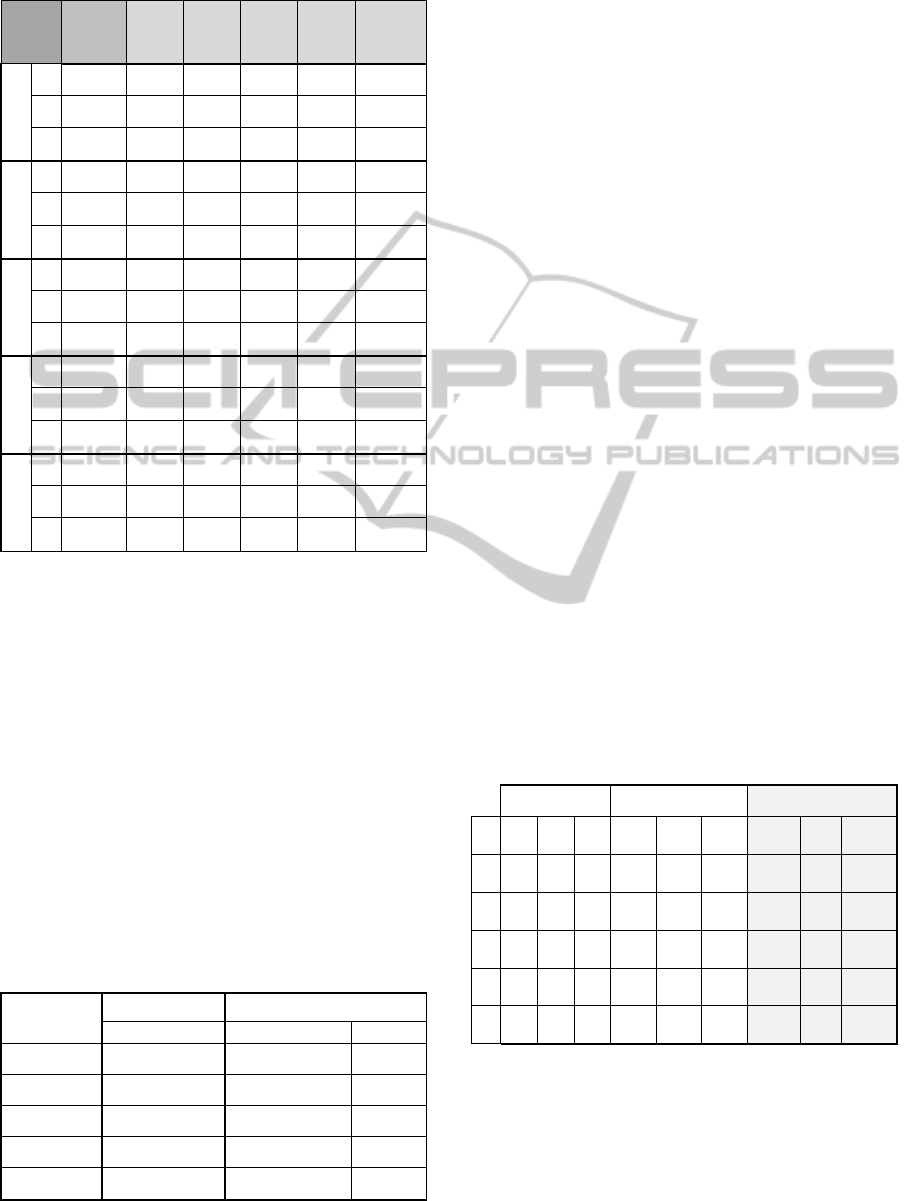
Table 2: Results on 15 Sudoku samples (i: iterations, t:
time in seconds.
#prb
success
rate%
maxi mini avgi
max
t
avgt
1
a 100 568 30 188 30 9.7
b 90 320 2 52 14 2.4
c 80 5472 243 2298 281 113
2
a 90 3427 616 1765 179 90
b 80 6994 858 2962 345 149
c 30 2007 367 952 95 45
3
a 80 1923 432 1156 96 59
b 20 8046 4116 6081 404 307
c 20 1434 918 1176 73 59
4
a 30 1831 874 1214 89 61
b 0 ‐‐‐‐ ‐
c 40 4165 343 1982 236 105
5
a 20 5345 123 2734 274 126
b 20 5036 4318 4677 235 222
c 10 4210 4210 4210 207 207
our VNS, even it failed to solve level 4 label b
within 10 tries, but it shows an acceptable rate of
success equal to 30% and 40% for labels a and c
respectively. The worst results are in level 5 with
only 10% successfully, the most difficult level (level
5) needs average of iterations between 2000 and
4000 to solve it 2 times out of 10 in a and b.
5.1 Comparing with HS
Harmony Search (HS) algorithm is tested with five
Sudoku instances in (Satyendra and Saumi, 2013).
Table 3 shows that our algorithm
outperform HS in
most of the experiments except the first problem
which is supposed to be the easier one among 5
problems. Our algorithm can solve this problem only
Table 3: Comparing VNS with HS.
#problem
HS VNS
SuccessRate% SuccessRate% timeavg
1 100 30 14.4
2‐ 90 1.7
3 35 100 0.051
4 15 40 19.9
5 10 90 27.5
3 times out of 10 tries. Interestingly, we can solve
instance of level 3 in very short time with average of
51 ms in rate of success equal to 100%. It seems not
to be so difficult or at least it has medium difficulty
because it has 52 fixed cells which seems to be solve
easily even by human. It’s clear that our algorithm
outperforms HS in success rate with fast average
time equal to 12.65 second.
5.2 Comparing with CA and GA
Finally, we compare our results with the results of
CA (Mantere and Koljonen, 2008), and NGA
(Xiuqin, Yongda and Ruichu, 2012) in Table 4.
Because that our algorithm is a trajectory-based
metaheuristic and their algorithms are population-
based algorithms, we think it’s not fair to comparing
number of generations with our number of iterations
as a comparing criterion. Instead, we believe rate of
success is important criterion as well as it is
common criterion between different algorithms. The
values in the table stand for success of rate in
finding optimal solution (fitness 0). As example the
first value under column (a) of CA algorithm means
the CA can solve the instance (a) 56 times out of
100, or the success rate is 56%. In NGA algorithm,
(<10) means that in 100 times trying, it can solve the
instance less than 10 times. From Table 4 we can
conclude that our algorithm gives us very
competitive results. The bold numbers mean the best
results in this table. It’s clear that our algorithm have
higher results in 10 instances and competitive results
in general.
Table 4: Comparison between CA, NGA and VNS in
terms of success rate.
CA NGA VNS
#
a b c a b c
a b c
1
5
6
7
6
4
6
10
0
10
0
100
100
90 80
2
4
2
2
2
2
2
40 30
40
90 80
30
3
4
2
1
9
1
7
20 10
30
80 20
20
4 7 7
1
3
10
20
<1
0
30
0
40
5 4 8 9
<1
0
<1
0
<1
0
20 20 10
6 CONCLUSIONS
In this paper, we propose a VNS-based algorithm for
solving the Sudoku problem and examine the
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
330

performance of our algorithm based on solution
quality. Well-known variation of VNS which is the
combination of VNS and VND is implemented and
tested on three different levels Sudoku problems.
The proposed algorithm gives competitive results in
easy level and promising results in medium levels
problems.
This is a preliminary work on the Sudoku. In the
future we would like to improve our proposed VNS
algorithm by testing new combination of
neighborhood structures and other variation of VNS:
Reduced VNS in local search phase to improve
solution quality and execution time.
REFERENCES
Asif, M., 2009. ‘Solving NP-complete problem using
ACO algorithm’, in Proceedings of International
Conference on Emerging Technologies, IEEE
Computer Society pp. 13–16.
Crawford, B., Aranda, M., Castro, C., & Monfroy, E.,
2008. ‘Using constraint programming to solve Sudoku
puzzles’, in Proceedings of the third international
conference on convergence and hybrid information
technology (ICCIT),IEEE Computer Society, pp. 926–
931.
Gunther, J., & Moon, T. K., 2012. Entropy minimization
for solving Sudoku, IEEE Transactions on Signal
Processing, 60(1), pp. 508–513.
Lewis, R., 2007. Metaheuristics can solve Sudoku Puzzles,
Journal of Heuristics, pp.387-401
Li, Y.D.
,
Deng, X.Q., 2011. Solving Sudoku puzzles base
on improved genetic algorithm, Comput. Appl. Softw.
, vol. 28(3), pp.68-70.
Mladenovic, M., Hansen, 1997. Variable neighborhood
search,Computers and Operations Research, Vol.24,
pp. 1097–1100
Mantere, T. and Koljonen, J., 2007. Solving, Rating and
Generating Sudoku Puzzles with GA, in Proceedings
of the 2007 IEEE Congress on Evolutionary
Computation-CEC2007, Singapore, pp. 1382-1389 .
Mantere, T. and Koljonen, J., 2008. Solving and analyzing
Sudokus with cultural algorithms, in Proceedings of
the 2008 IEEE Congress Computational Intelligence -
WCCI2008, 1-6 June, Hong Kong, China, pp. 4054-
4061.
Mantere, T., Koljonen, J., 2009. Ant Colony Optimization
and a Hybrid Genetic Algorithms for Sudoku Solving,
in Proceedings of the 15th International Conference
on Soft Computing, Brno, Czech Republic, Mendell,
pp.41-48.
Satyendra, M., Saumi, S., 2013. Solution and Level
Identification of Sudoku Using Harmony Search, I.J.
Modern Education and Computer Science, pp. 49-55.
Simonis, H., 2005. Sudoku as a constraint problem, in
Proceedings of the 4th International workshop on
modelling and reformulating constraint satisfaction
problem, pp. 13–27.
Xiuqin, D., Yongda, Y., Ruichu, C., 2012. Sudoku with
New Genetic Algorithm, in Proceedings of the
international Conference on Artificial Intelligence and
Soft Computing Lecture Notes in Information
Technology, Vol.12, pp 431-440
Yato, T. and Seta, T., 2003. Complexity and Completeness
of Finding Another Solution and Its Application to
Puzzles, IEICE Trans. Fundamentals, E86-A (5),
p.1052– 1060.
AVariableNeighborhoodSearchforSolvingSudokuPuzzles
331
