A Word Association Based Approach for Improving Retrieval
Performance from Noisy OCRed Text
Anirban Chakraborty
1
, Kripabandhu Ghosh
1
and Utpal Roy
2
1
Computer Vision and Pattern Recognition Unit, Indian Statistical Institute, 203 B. T. Road, Kolkata 700108, India
2
Department of Computer and System Sciences, Siksha-Bhavana, Visva-Bharati, Santiniketan 731235, India
Keywords:
Erroneous Text, Cooccurrence, Pointwise Mutual Information.
Abstract:
OCR errors hurt retrieval performance to a great extent. Research has been done on modelling and correction
of OCR errors. However, most of the existing systems use language dependent resources or training texts
for studying the nature of errors. Not much research has been reported on improving retrieval performance
from erroneous text when no training data is available. We propose an algorithm of detecting OCR errors and
improving retrieval performance from the erroneous corpus. We present two versions of the algorithm: one
based on word cooccurrence and the other based on Pointwise Mutual Information. Our algorithm does not
use any training data or any language specific resources like thesaurus. It also does not use any knowledge
about the language except that the word delimiter is a blank space. We have tested our algorithm on erroneous
Bangla FIRE collection and obtained significant improvements.
1 INTRODUCTION
Erroneous text collections have posed challenges to
the researchers. Many such collections have been
created and the researchers have tried several er-
ror modelling and correcting techniques on them.
The techniques involve training models on sam-
ple pairs of correct and erroneous variants. But
such exercise is possible only if the training sam-
ples are available. There are several text collec-
tions which are created directly by scanning hard
copies and then OCRing them. Such collections in-
clude the Million Book Project collection (archived
at http://deity.gov.in/content/national-digital-library)
and ACM SIGIR Digital Museum (archived at
www.sigir.org/museum/allcontents.html). Millions of
court documents, defence documents, proprietary and
legacy documents are in hard-copy format also con-
tribute to the vast collections of documents which lack
the original error-free version.
The unavailability of training data presents a dif-
ferent problem premise. To the best of our knowl-
edge, the first such endeavour to address the problem
was done by Ghosh et al. (Ghosh and Chakraborty,
2012) (we will refer to this work as RISOT2012) in
FIRE 2012 RISOT track. They proposed an algo-
rithm based on word similarity and context infor-
mation. A string matching technique (e.g., edit dis-
tance, n-gram overlaps, etc.) alone is not reliable in
finding the erroneous variants of an error-free word
due to homonymy. For example, word pairs like in-
dustrial and industrious, Kashmir (place) and Kash-
mira (name), etc. have very high string similarity
and yet they are unrelated. Such mistakes are even
so likely when we do not have a parallel error-free
text collection to match the erroneous variants with
the correct ones using the common context. How-
ever, context information can be used to get more re-
liable groups of erroneous variants. Context informa-
tion can be harnessed effectively by word cooccur-
rence. We say that two words cooccur if they occur in
a window of certain words between each other. Word
cooccurrence have been used successfully in identi-
fying better stems (Paik et al., 2011a), (Paik et al.,
2011b) than methods that use string similarity only
(Majumder et al., 2007). In this paper, we propose
an approach that also uses word association measures
like word cooccurrence and Pointwise Mutual Infor-
mation. Pointwise Mutual Information (PMI) also
gives good measure of association between words.
Kang et al. (Kang and Choi, 1997) showed that PMI
between query and document words can be used ef-
fectively in improving natural language information
retrieval. So, we have used both these word associa-
tion measures for our experiments in this paper. We
show that our approach outperforms RISOT2012.
450
Chakraborty A., Ghosh K. and Roy U..
A Word Association Based Approach for Improving Retrieval Performance from Noisy OCRed Text.
DOI: 10.5220/0005157304500456
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2014), pages 450-456
ISBN: 978-989-758-048-2
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

The rest of the paper is organised as follows:
In section 2, we discuss the related works. In sec-
tion 3, we describe our method. We present the results
in section 4. We conclude in section 5.
2 RELATED WORK
Some works have been reported on retrieval from
OCRed text. Among the earliest works, Taghva et
al. (K. Taghva and Condit, 1994) applied probabilis-
tic IR on OCRed text. Here, error correction was done
using a domain-specific dictionary. A. Singhal et al.
(A. Singhal and Buckley, 1996) showed that the linear
document normalization models were better suited to
collections containing OCR errors than the quadratic
(cosine normalization) models. TREC made a signif-
icant effort on the study and effect of OCR errors in
retrieval in their two tasks: the Confusion Track and
the Legal Track. The TREC Confusion track was a
part of the TREC 4 (1995) (Harman, 1995) and TREC
5 (1996) (Kantor and Voorhees, 1996). In TREC 4
Confusion Track, random character insertions, dele-
tions and substitutions were used to model degra-
dations. For the TREC 5 Confusion Track, 55,000
government announcement documents were printed,
scanned, OCRed and then were used. Electronic text
for the same documents was available for comparison.
Participants experimented with techniques that used
error modelling to alleviate OCR errors using charac-
ter n-gram matches.
A similar track, RISOT (Garain et al., 2013),
was offered in Forum for Information Retrieval Eval-
uation (FIRE) (www.isical.ac.in/∼fire) 2011. This
was aimed at improving retrieval performance from
OCRed text in Indic script. Here a set of FIRE Bangla
collection of 62,825 documents was available as the
“TEXT” or “clean” collection from leading Bangla
newspapers, Anandabazar Patrika. Each document
of the collection was scanned at a resolution of 300
dots per inch. Then, each scanned document was
converted to electronic text using a Bangla OCR sys-
tem that had about 92.5% accuracy. Ghosh et al.
(Ghosh and Parui, 2013) performed a two-fold error
modelling technique for OCR errors in Bangla script.
In 2012 RISOT, in addition to the Bangla collection
pair, a Hindi collection pair was also offered. The
error-free Hindi document collection is created from
leading Hindi newspapers Dainik Jagaran and Amar
Ujala. The OCRed Hindi collection was created using
a Hindi OCR system which also had 92.5% accuracy.
However, one can find substantial work in the lit-
erature on OCR error modelling and correction. Ko-
lak and Resnik (Kolak and Resnik, 2002) applied a
pattern recognition approach in detecting OCR errors.
Walid and Kareem (Magdy and Darwish, 2006) used
Character Segment Correction, Language modelling,
and Shallow Morphology techniques in error correc-
tion on OCRed Arabic texts. On error detection and
correction of Indic scripts, B.B. Chaudhuri and U. Pal
produced the very first report in 1996 (Chaudhuri and
Pal, 1996). This paper used morphological parsing
to detect and correct OCR errors. Separate lexicons
of root-words and suffixes were used. Fataicha et al.
(Fataicha et al., 2006) located confused characters in
erroneous words and performed to create a collection
of erroneous error-grams. Finally, they generated ad-
ditional query terms, identified appropriate matching
terms, and determined the degree of relevance of re-
trieved document images to the user’s query, based on
a vector space IR model.
3 OUR APPROACH
3.1 Key Terms
3.1.1 Word Cooccurrence
We say that two words, say, w
1
and w
2
, cooccur if
they appear in a window of size s (s > 0) words in
the same document d. Suppose, the words w
1
and
w
2
cooccur in a window of size 5 in a document d.
This means that there is at least one instance in the
document where at most 4 words (distinct from w
1
and w
2
) occur between w
1
and w
2
or between w
2
and
w
1
. Let cooccurFreq
(d,s)
(w
1
, w
2
) denote the number
of times w
1
and w
2
cooccur in d in a window of size
s. Then, we call cooccurFreq
(d,s)
(w
1
, w
2
) the cooc-
currence frequency of w
1
and w
2
in document d for a
window of size s. However, it is a common practice
to calculate cooccurFreq
(d,s)
(w
1
, w
2
) over all the doc-
uments in a collection. This is likely to give a more
robust measure of co-location of the words w
1
and w
2
.
Word cooccurrence gives a reliable measure of as-
sociation between two words as it reflects the degree
of context match between the two words. Usually,
the total cooccurrence between word pairs is calcu-
lated over a collection of documents by summing up
the document-wise cooccurrence frequencies. High
cooccurrence between a pair of words is an indicator
of high degree of relatedness of the words. This as-
sociation measure gets more strength when it is used
in conjunction with a string matching measure. For
example, two words sharing a long stem (prefix) is
likely to be variants of each other if they share the
same context as indicated by a high cooccurrence
value between them. The word industrious shares a
AWordAssociationBasedApproachforImprovingRetrievalPerformancefromNoisyOCRedText
451

stem “industri” with the word industrial. But, they
are not variants of each other. They can be easily
segregated by examining their context match as they
are unlikely to have a high cooccurrence frequency.
In this paper, we have used cooccurrence informa-
tion with a string similarity measure (LCS, discussed
shortly afterwards) to identify erroneous variants of
query words.
3.1.2 Pointwise Mutual Information
Pointwise mutual information (PMI) is a measure of
association used in information theory and statistics.
Let W
1
and W
2
be two events that the words w
1
and
w
2
respectively occur in a document. We define PMI
as follows:
PMI(W
1
,W
2
) = log(
P(W
1
W
2
)
P(W
1
)P(W
2
)
)
o
(1)
where P(W
1
W
2
) is the probability that the words
w
1
and w
2
occur in the same document, P(W
1
), P(W
2
)
are the probabilities that the words w
1
and w
2
occur
in a document respectively.
Now PMI expression (1) can be further written as
PMI(W
1
,W
2
) = log(
nOCC(w
1
w
2
)
N
nOCC(w
1
)
N
.
OCC(w
2
)
N
)
= log(
nOCC(w
1
w
2
)
nOCC(w
1
).nOCC(w
2
)
.N),
where nOCC(w
1
w
2
) is the number of documents
in which the words w
1
and w
2
occur together,
nOCC(w
1
), nOCC(w
2
) are the numbers of documents
in which the words w
1
and w
2
occur respectively, N
is the total number of documents in the corpus. So,
nOCC(w
1
w
2
) is nothing but the cooccurrence of the
words w
1
and w
2
in the whole document over the cor-
pus. So, PMI is another measure of word associa-
tion. Two words are said to have high association
if P(W
1
W
2
) > P(W
1
)P(W
2
) for which PMI(W
1
,W
2
)
> 0. If there is very little association between the
words, P(W
1
W
2
) ≈ P(W
1
)P(W
2
) so that PMI(W
1
,W
2
)
≈ 0. Finally, if the words are negatively associ-
ated (i.e., one appears only in the absence of the
other), P(W
1
W
2
) < P(W
1
)P(W
2
) and consequently,
PMI(W
1
,W
2
) < 0. So, we only consider those words
to be associated for which the PMI value is positive.
3.2 Longest Common Subsequence
(LCS) Similarity
Given a sequence X = hx
1
, x
2
,....,x
m
i, another se-
quence Z = hz
1
, z
2
,....,z
k
i is a subsequence of X if
there exists a strictly increasing sequence hi
1
, i
2
,....,i
k
i
of indices of X such that for all j = 1,2,...,k, we have
Figure 1: Similar neighbours.
Figure 2: Dissimilar neighbours.
x
i
j
= z
j
. Now, given two sequences X and Y, we say
that Z is a common subsequence of X and Y if Z is
a subsequence of both X and Y. A common subse-
quence of X and Y that has the longest possible length
is called a longest common subsequence or LCS of X
and Y. For example, let X = hA, B,C, B, D, A, Bi and
Y = hB, D,C, A, B, Ai. Then, the sequence hB,D,A, Bi
is the LCS of X and Y. In general, LCS of two se-
quences is not unique.
In our problem, we consider sequences of charac-
ters or strings. For strings industry and industrial, an
LCS is industr. Now, we define a similarity measure
as follows:
LCS
similarity(w
1
, w
2
)
=
StringLength(LCS(w
1
,w
2
))
Maximum(StringLength(w
1
),StringLength(w
2
))
So, LCS
similarity(industry, industrial)
=
StringLength(LCS(industry,industrial))
Maximum(StringLength(industry),StringLength(industrial))
=
StringLength(industr)
Maximum(8,10)
=
7
10
= 0.7
Note that the value of LCS
similarity lies in the
interval [0,1].
3.3 The Proposed Approach
Our approach has two basic steps:
1. Clustering
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
452

2. Cluster selection
These steps are discussed in detail as follows:
1. Clustering
We have used the notion of social relatedness as
the pivotal point of our clustering algorithm. In
this work we have measured relatedness using
cooccurrence and PMI. In this problem, we say
that two words share the same neighbourhood of
each other if they appear in the same document
and have some degree of string similarity. How-
ever, there can be words which have high string
similarity and are variants of each other. But,
they do not cooccur in the same document. We
attempt to bridge the relationship between these
words using the words which are common neigh-
bours. In other words, a word w is a common
neighbour of words w
1
and w
2
if w cooccurs with
w
1
and w
2
in different documents but w
1
and w
2
do not cooccur with each other. For this pur-
pose, we have considered two degrees of related-
ness between two words. First we consider that
two words have a common neighbour. These two
words are similar neighbours of each other if they
also have high string similarity. This situation is
shown in Figure 1. Here Tobacco and Tobacc0
share a common neighbour Tobacc1. Hence, To-
bacco and Tobacc0 become similar neighbours as
they have high string similarity. Secondly, we say
that two words are dissimilar neighbours if they
have a common neighbour which has low string
similarity with both. However, these two words
are highly similar and are connected by the dis-
similar word. This situation is shown in Figure
2. Here, Tobacco and Tobacc are connected by
Cigarette. In Figure 1, we say that Tobacc1, To-
bac and obacc are close neighbours of Tobacco
since they appear in the same document with To-
bacco and have high string similarity with To-
bacco. However, Cigarette, Smoking and Cancer
are not close neighbours of Tobacco because they
only cooccur with Tobacco but are not erroneous
variants of Tobacco. Algorithm 1 elaborates the
idea.
In Algorithm 1, at step 1 we consider the set of
all the words L in the erroneous corpus and the set
of all the query words Q. Note that L contains er-
roneous words while Q contains error free words.
At step 3, we generate a query specific subset L
wq
of L based on string similarity. Step 7 gets the
close neighbours of w. We refer the Figure 1. For
the word Tobacco, {Tobacc1, Tobac and obacc}
are the close neighbours. Step 8 gets the simi-
lar neighbours of the close neighbours obtained
in the previous step. Tobacc0 is one similar neigh-
Algorithm 1: Clustering and Selection algorithm.
1: Let L be the set of all unique words in the corpus.
Let Q be the set of all unique words in all the
queries.
2: for each word wq in Q do
3: Let L
wq
be subset of L containing all the words
ww in L such that LCS
similarity(wq, ww)
greater than some threshold α (> 0)
4: for each word w in L
wq
do
5: S
w
closesimilar
= S
w
dissimilar
=
/
0 ; let S
w
=
S
w
closesimilar
∪ S
w
dissimilar
6: /* Clustering */
7: For word w
1
cooccurring with w, calculate
LCS
similarity between w and w
1
. Store
w
1
in S
w
closesimilar
if LCS similarity(w, w
1
) >
some threshold β (> 0)
8: For each w
′
in S
closesimilar
, find the
words w
2
cooccurring with w
′
such that
LCS
similarity(w, w
2
) > β. Include all these
words in S
w
closesimilar
.
9: Repeat step (8) until no new word is added
to S
w
closesimilar
.
10: Consider top m (in terms of frequency in
corpus) words cooccurring with w.
11: For each such word w
3
, find the words
w
4
cooccurring with w
3
such that
LCS similarity(w, w
4
) > β. Include all
these words in S
w
dissimilar
12: Repeat step (11) until no new word is added
to S
w
dissimilar
.
13: Finally we get S
w
for the word w
14: end for
15: /* Cluster selection */
16: Calculate LCS
similarity(wq, w
C
), for all the
words w
C
in the clusters S
w
, where w ∈ L
wq
17: Choose the cluster for which
LCS
similarity(wq, w) for atleast one word w
in the cluster is the maximum among all the
words in all the clusters S
w
, where w ∈ L
wq
.
Name this cluster C
wq
. If the number of such
clusters is more than one, merge all of them to
form a composite cluster C
wq
18: Expand wq with C
wq
19: end for
bour of Tobacco obtained through the common
neighbour Tobacc1. So, at the end of step 9,
S
closesimilar
contains all the close neighbours and
similar neighbours of w. At step 10, we consider
the neighbours (not necessarily the close neigh-
bours) of w which have high cooccurrence with
w. These neighbours do not necessarily have high
similarity with w. In Figure 2, Cigarette, Smok-
ing and Cancer are such neighbours of Tobacco.
AWordAssociationBasedApproachforImprovingRetrievalPerformancefromNoisyOCRedText
453

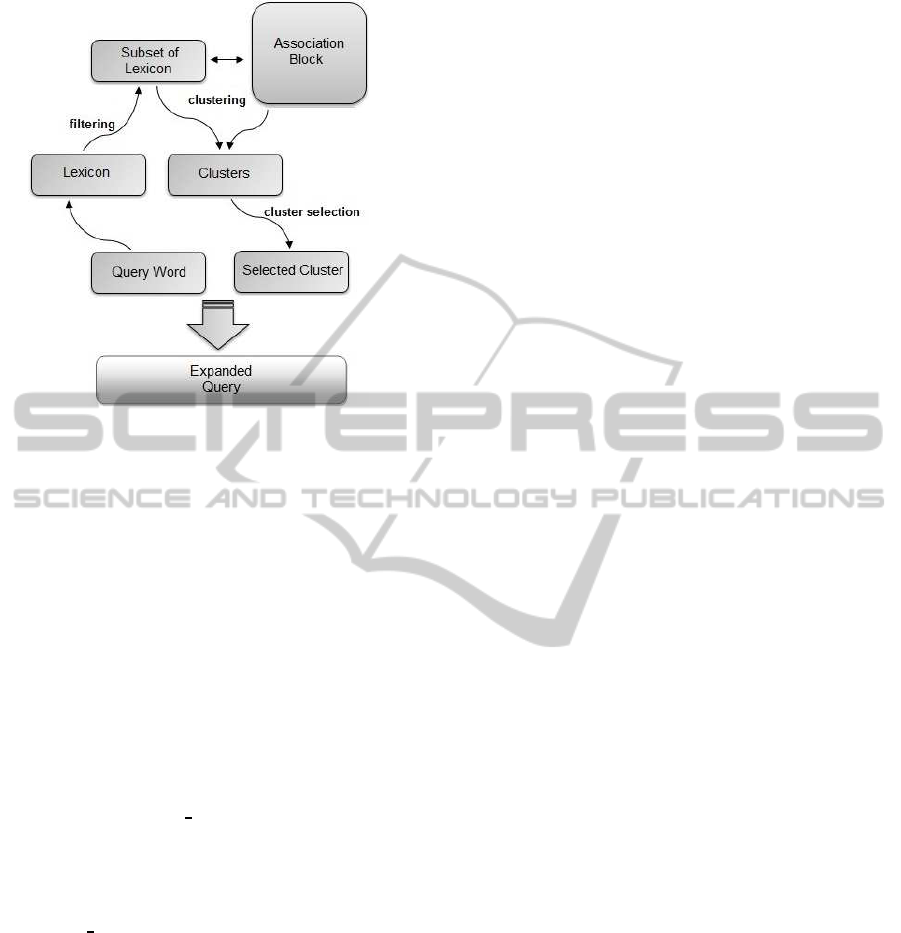
Figure 3: Proposed approach: pictorial view.
At step 12, we get the dissimilar neighbours of w.
Tobacc is a dissimilar neighbour of Tobacco. Fi-
nally, at step 13, we get all the close, similar and
dissimilar neighbours of w.
2. Cluster Selection
The remaining part of Algorithm 1 deals with the
selection of the appropriate cluster for a given
query word. By appropriate cluster of a query
word w
q
, we mean the cluster containing words
of the OCRed corpus that contain the variants of
w
q
. At the end of step 14, we have obtained a
number of clusters for a given query word wq.
The number of such clusters is same as the num-
ber of words selected from L at step 3. At step
16, we compute LCS similarity of wq with all the
words in the clusters formed at step 13 of the al-
gorithm. Suppose for query word Tobacco, we
get the two clusters C
1
= {Tobacc, Tobac, 1bacc}
and C
2
= {obacc, bacco, Tobaccos}. We calcu-
late LCS
similarity of Tobacco with the six words
in the two clusters. The highest similarity of To-
bacco is with Tobaccos, which is 0.875. Accord-
ing to step 17, we select C
2
as the expansion of
Tobacco. So, the query word Tobacco gets ex-
panded to the query {Tobacco, obacc, bacco, To-
baccos}. If both the clustersC
1
andC
2
had a word
each such that both the words had the maximum
similarity with Tobacco, we would have merged
C
1
and C
2
to a composite cluster, say, C such that
C = C
1
∪ C
2
. Then the expanded version of wq
would have been {wq} ∪ C.
• PMI version: We have also developed a PMI
version of Algorithm 1. For this version, we
have incorporated some refinements at steps 7,
8, 10 and 11 of Algorithm 1. In the PMI ver-
sion, if w
1
is chosen for inclusion in S
w
closesimilar
according to Algorithm 1 at step 7, we cal-
culate PMI(W, W
1
), where W and W
1
are the
events that the words w and w
1
respectively
have occurred in a document. In this version of
the algorithm, w
1
is added to S
w
closesimilar
only
if PMI(W, W
1
) > 0. Similarly, at step 8, w
2
is added to S
w
closesimilar
only if PMI(W, W
2
) >
0, where W
2
is the event that w
2
has occurred
in a document. At step 10, the top m words
are selected on the basis of PMI values instead
of cooccurrence frequencies. Here only those
words are considered which have positive PMI
with w. Again, at step 11 only those words
are considered for inclusion in S
w
dissimilar
which
have positive PMI with w. So, the PMI version
is more restrictive.
A pictorial view of the proposed approach is
shown at Figure 3. Corresponding to a Query
Word the Lexicon is filtered using LCS similarity
to form a Subset of Lexicon. Next, we apply our
clustering algorithm to cluster Subset of Lexicon
into Clusters using the Association Block. The
Association Block contains pairwise word associ-
ation values i.e., Cooccurrence frequency or PMI,
depending upon the version of the algorithm used.
From the set of Clusters we apply our cluster se-
lection strategy to select a single Selected Cluster.
Now, the union of the Query Word and Selected
Cluster gives the Expanded Query.
3.3.1 Improvements over RISOT2012
Our approach is a refinement of RISOT2012 (Ghosh
and Chakraborty, 2012) in a sense that both the meth-
ods utilize word association in clustering erroneous
word variants. However, we have incorporated some
vital modifications in the course of developing our al-
gorithm. The changes are as follows:
1. RISOT2012 clusters the whole corpus. This is
inconvenient in two ways. Firstly, its time con-
suming. Secondly, it complicates the method of
identifying the correct variants of a given query
word from the whole set of clusters. In our al-
gorithm, we have, therefore, followed a query
specific scheme for creating the word association
clusters. This provides a more reliable scheme
of identifying appropriate candidates for a query
word.
2. RISOT2012 uses a complicated scheme for select-
ing the appropriate clusters for query expansion.
We have simplified this step to a great extent.
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
454

3. RISOT2012 uses only word cooccurrence as the
measure for word association. We have used both
cooccurrence and PMI and presented a compari-
son of the two word association measures.
Finally, we have referred to the above steps as
improvements over RISOT2012 because the proposed
method produces notable improvements over the for-
mer, as presented in the Results section.
4 RESULTS
4.1 Dataset
We tested our algorithm on FIRE RISOT
(http://www.isical.ac.in/∼fire/data.html) Bangla
collection. The collection statistics can be seen in
Table 1. Bangla original is the “clean” or error-free
version created from Anandabazar Patrika. Bangla
OCRed is the scanned-and-OCRed version of the
same. A document in the original version and its
OCRed version had the same unique document
identification string so that the original-OCRed pairs
can be easily identified. We can see that original
version contains more documents than its OCRed
version. So, naturally, the extra documents in the
original could not be used for comparison. But,
despite having fewer documents, we can see that
the OCRed collection contains more unique terms
than its error-free counterpart. The number of unique
terms for Bangla original corpus is 396968 while the
same number for its OCRed version is 466867. This
discrepancy is caused by OCR errors. Most of the
inflations are caused by misrecognitions (as multiple
candidates), word disintegrations and several other
distortions. The Bangla collection has 66 topics.
These topics were created for previous FIRE Ad Hoc
tasks. A subset of the Ad Hoc topics were selected
for the RISOT task.
4.2 Parameters
The proposed approach has three parameters α, β and
m. For determining the values of α and β, we have run
Grid Search in the interval [0.4, 1] for each of the two
parameters at step lengths of 0.01. We have chosen m
as 10. Out of the results obtained from several combi-
nations of the parameter values, we have reported the
best results for both the versions: Coocurrence and
PMI.
4.3 Evaluation
Table 2 shows the results. We have evaluated our runs
Table 1: Collection statistics.
No. No. No.
Dataset of of of
documents topics unique terms
Bangla original 62838 66 396968
Bangla OCRed 62825 66 466867
Table 2: Results in MAP.
Run MAP
Original 0.2567
OCRed 0.1791
RISOT2012 0.1974
Proposed Cooccurrence 0.2067 (+15.41%)
Proposed PMI 0.2060 (+15.02%)
on Mean Average Precision (MAP). Original is the
result when all the queries are run on the “clean”
or error-free version of the corpus. This value can
be considered as an upper bound for performance.
OCRed is the result when the same set of queries are
run on the OCRed version of the corpus. RISOT2012
is the Ghosh et al. (Ghosh and Chakraborty, 2012)
method run on the OCRed corpus. Proposed Cooc-
currence is the result produced by our method on the
OCRed corpus when the Cooccurrence version of our
algorithm is used. Proposed PMI is the result pro-
duced on the OCRed corpus when the PMI version
is used. We see that our method yields numerical
improvements over OCRed text and RISOT2012 for
both the versions and these differences were found to
be statistically significant at 95% confidence level (p-
value < 0.05) by Wilcoxon signed-rank test (Siegel,
1956). The table shows % improvements of the pro-
posed methods over OCRed. However, the proposed
approach is not as good as the retrieval result from
original corpus for both the Cooccurrence and PMI
versions.
5 CONCLUSIONS
In this work we have addressed a new problem
premise and made an effort to come up with a possible
solution. We have shown that it is possible, to an ex-
tent, to improveretrieval performance from erroneous
text even if the clean version is not available for er-
ror modelling. We have produced improvement over
a similar approach through crucial refinements. We
see that harnessing the context information (through
word cooccurrence or PMI) gives a reliable measure
of grouping inflectional error variants. However, the
use of cooccurrence and PMI separately shows that
there is not much numerical difference between the
two in the final result. The proposed method can be
of practical use as it can be used effectively to retrieve
AWordAssociationBasedApproachforImprovingRetrievalPerformancefromNoisyOCRedText
455

important information from the collections which do
not have an error-free text version. The proposed ap-
proach is language-independent and so can be used
across different text collections without language spe-
cific resources. So, we are looking forward to apply
it on other noisy collections like RISOT 2012 Hindi
and TREC Legal IIT CDIP.
ACKNOWLEDGEMENTS
We express our sincere gratitude towards Prof. Swa-
pan Kumar Parui, Indian Statistical Institute, Kolkata,
India for his support and guidance.
REFERENCES
A. Singhal, G. S. and Buckley, C. (1996). Length normal-
ization in degraded text collections. pages 149–162. In
Proceedings of the Fifth Annual Symposium on Doc-
ument Analysis and Information Retrieval.
Chaudhuri, B. and Pal, U. (1996). Ocr error detection and
correction of an inflectional indian language script.
Pattern Recognition, 3:245 – 249.
Fataicha, Y., Cheriet, M., Nie, Y., and Suen, Y. (2006). Re-
trieving poorly degraded ocr documents. Int. J. Doc.
Anal. Recognit., 8(1):1–99999.
Garain, U., Paik, J., Pal, T., Majumder, P., Doermann, D.,
and Oard, D. (2013). Overview of the fire 2011 risot
task. volume 7536. Springer.
Ghosh, K. and Chakraborty, A. (2012). Improving ir per-
formance from ocred text using cooccurrence. FIRE
RISOT track 2012 working notes.
Ghosh, K. and Parui, S. K. (2013). Retrieval from ocr text :
Risot track. volume 7536, pages 214–226. Springer.
Harman, D. (1995). Overview of the fourth text retrieval
conference. pages 1–24. The Fourth Text Retrieval
Conference.
K. Taghva, J. B. and Condit, A. (1994). Results of apply-
ing probabilistic ir to ocr text. pages 202–211. In The
Proceedings of the 17th Annual International ACM
SIGIR Conference on Research and Development in
Information Retrieval.
Kang, H.-K. and Choi, K.-S. (1997). Two-level docu-
ment ranking using mutual information in natural lan-
guage information retrieval. Inf. Process. Manage.,
33(3):289–306.
Kantor, P. and Voorhees, E. (1996). Report on the trec-5
confusion track. pages 65–74. The Fifth Text Retrieval
Conference.
Kolak, O. and Resnik, P. (2002). Ocr error correction us-
ing a noisy channel model. pages 257–262. Proceed-
ings of the Second International Conference on Hu-
man Language Technology Research.
Magdy, W. and Darwish, K. (2006). Arabic ocr error cor-
rection using character segment correction, language
modeling, and shallow morphology. pages 408–414.
In Proceedings of the 2006 Conference on Empirical
Methods in Natural Language Processing.
Majumder, P., Mitra, M., Parui, S. K., Kole, G., Mitra, P.,
and Datta, K. (2007). Yass: Yet another suffix stripper.
ACM Trans. Inf. Syst., 25(4).
Paik, J. H., Mitra, M., Parui, S. K., and J¨arvelin, K.
(2011a). Gras: An effective and efficient stemming
algorithm for information retrieval. ACM Trans. Inf.
Syst., 29(4):19:1–19:24.
Paik, J. H., Pal, D., and Parui, S. K. (2011b). A
novel corpus-based stemming algorithm using co-
occurrence statistics. In Proceedings of the 34th inter-
national ACM SIGIR conference on Research and de-
velopment in Information Retrieval, SIGIR ’11, pages
863–872, New York, NY, USA. ACM.
Siegel, S. (1956). Nonparametric statistics for the behav-
ioral sciences. McGraw-Hill series in psychology.
McGraw-Hill.
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
456