
A New Artificial Neural Network Approach
for Fluid Flow Simulations
Osama Sabir
1
and T. M. Y. S. Tuan Ya
2
1
Faculty of Engineering, Universiti Teknologi Petronas, Petronas, Malaysia
2
Department of Mechanical Engineering, Petronas, Malaysia
Keywords: Artificial Neural Networks (ANNS), Flow Visualization, Flow Velocity, Uniform Flow, Natural
Convection, Geometrical Boundaries Profile, Real Time Response Simulation.
Abstract: In this research we describe our attempt to get instantaneous numerical simulation for fluid flow by using
Artificial Neural networks (ANN). Such simulation should provide a reliable perception about the fluid
behaviour with respect to both momentum and energy equations. In addition to the preceding recorded data,
the proposed method consider the geometrical boundaries profile as a major contributions for ANN training
phase. Our study is driven by the need of rapid response especially in medical cases, surgeon diagnosis,
engineering emergency situations, and when novel circumstances occurs. Furthermore, the existing
computational fluid dynamics tools require long time to response and the present of professional expert to
set the parameters for the different cases. In fact, ANN can deal with the lack of proper physical models or
the present of uncertainty about some conditions that usually affect the outcomes form the other approaches.
We manage to get acceptable result for 1D-flow equations with respect to both energy and momentum
equations. Our ANN approach is able to handle fluid flow prediction with known boundaries velocity. This
approach can be the first step for neural network computational program that can tackle variance type of
problems.
1 INTRODUCTION
The ANN seem to be the right tool to find quick
results from recorded data due to its flexibility and
automatic perception. In fact, ANN can deal with the
lack of proper physical models or the present of
uncertainty about some conditions which usually
effect the outcomes form the other approaches.
Commonly, CFD solutions still have to be validated
against reliable results, such as experimental or
benchmarks data, in order to gain confidence in the
outcomes. Since we have to compare our results to
previous data why not try from start to use this
comparisons to predict the fluid characteristics and
get instant feedback. ANN has been employed in
heat and mass flow processes mostly in the present
of uncertainty conditions. There are several research
regarding the predictions of heat transfers, mass
flow rate, aerodynamic coefficients and statistical
quantities (Islamoglu et al., 2005, Liu et al., 2002,
Dı
́
az et al., 2001, Rajkumar and Bardina, Panigrahi
et al., 2003).
Motivated by Benning, Becker, and Delgado
(Benning et al., 2001, Benning et al., 2002)
propagation neural networks model to predict the
flow field for steady flow around a cylinder, we try
here to predict distributions of thermal and flow
variables in a domain. We reverse Hirschen and
Schäfer methodology (Hirschen and Schäfer, 2006)
to add the geometrical boundary as a major input for
our ANN model. They use ANN in conjunction with
evolutionary strategy to optimize the geometry for
fluid flow.
In the proposed paper, we first list the types of
the appropriate network architecture that can handle
the fluid characteristics efficiently. Second, we
choose the proper training method to insure accurate
and effective response from the numerical ANN
training database. Then, we combine geometrical
boundaries profile and the ANN training data to
generate the simulation. Finally, we discuss and
illustrate our initial results.
334
Sabir O. and M. Y. S. Tuan Ya T..
A New Artificial Neural Network Approach for Fluid Flow Simulations.
DOI: 10.5220/0005157503340338
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 334-338
ISBN: 978-989-758-054-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
2 METHODOLOGY
The MATLAB -Version 7.0 (R2010b) - Neural
Network Toolbox is used to simulate our ANN
model. The ANN training data is obtained from the
Analytic solution for the parabolic heat equations.
We start by building the numerical database to be
the ANN training data. The Crank–Nicolson method
and the implicit method is implemented to find the
numerical solution. The collections of known input-
output arrays from numerical data are exposed to the
neural network in order to teach it. Then the weight
factors between nodes are adjusted until the
specified input produces the wanted output. Through
these tunings, the ANN learns the correct input-
output flow predictions. Our ANN is applied to
transient two dimension domain to predict the flow
behaviour. Then we manipulate the network
architecture to ensure it can handle the fluid
characteristics efficiently. Finally, we test the ANN
responses under different training methods to make
sure the system is optimized.
The simple steady state heat transfer is validated
in order to test the ANN ability to predict the flow
characteristics. The geometrical boundaries is
investigated and its effect on the results is measured.
Our approach satisfy the energy and the momentum
equations tested a transient heat flow. The
MATLAB command tic-toc is used to calculate how
long the ANN response. Then the responses was
compared with other numerical results.
3 RESULTS
3.1 Steady State Heat Transfer
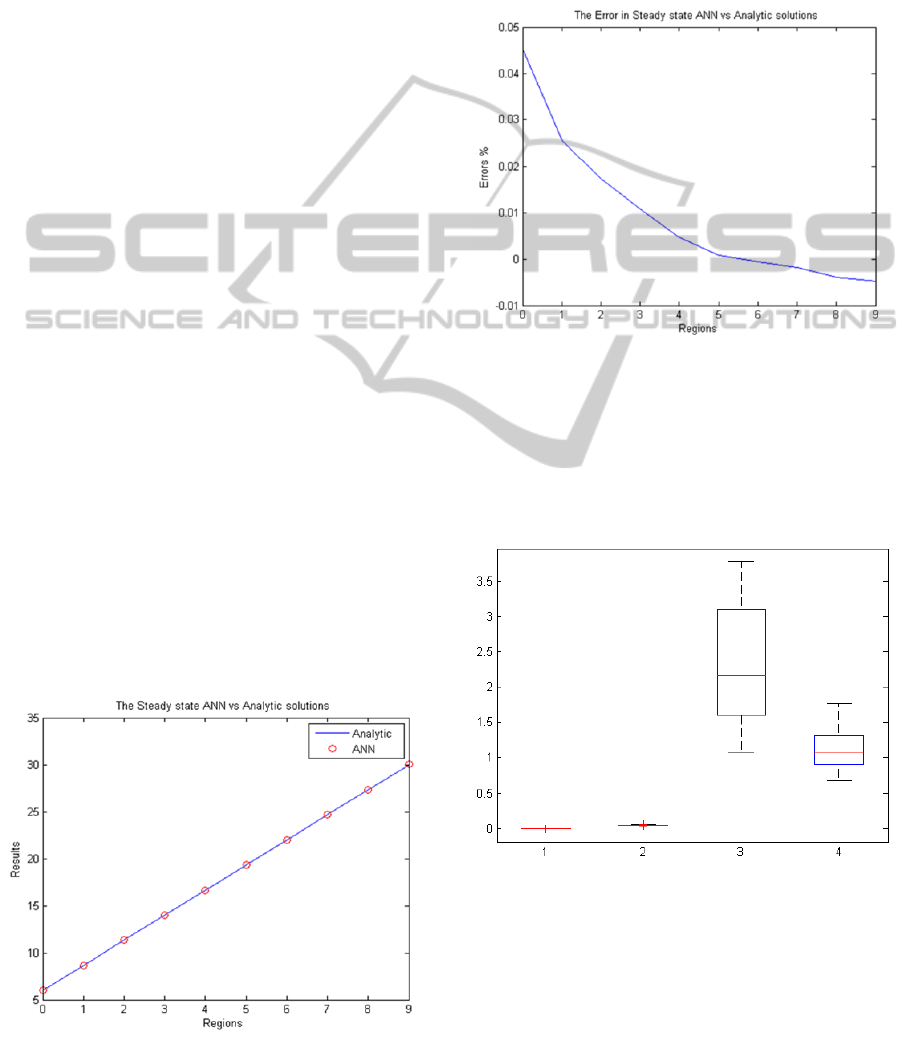
Figure 1: Steady State: - ANN vs Analytic result.
For steady state heat transfer simulation we manage
to get almost perfect match between the ANN output
and the analytic solutions. We divide our problem to
10 check points and following figures shows the
results and the errors.
The errors graph shows significant match
between the analytic results and our ANN.
Figure 2: Steady State:- Errors percentage.
For computations cost analysis we calculate the
time response for each methods. Although it is
possible to measure performance using the
cputime function, MATLAB suggest the use of
tic and toc functions for this purpose exclusively.
‘’
Figure 3: Time response for each Numerical methods.
The following table shows the time performance in
seconds for each methods.
ANewArtificialNeuralNetworkApproachforFluidFlowSimulations
335

Table 1: The Analysis of ANN Performance.
Analytic ANN
Crank–
Nicolson
method
Implicit
Method
0.000024 0.038119 3.77518588 1.33223522
0.000016 0.044691 3.60739191 0.71496448
0.000017 0.052277 3.49266863 1.35002134
0.000016 0.051744 1.95030985 1.28812227
0.000016 0.05467 1.21223425 1.15282111
0.000016 0.049609 2.88919158 1.55687154
0.000015 0.050025 3.66721568 1.03937439
0.000015 0.049784 1.79117658 1.76835897
0.000015 0.055496 2.11929139 1.11576155
0.000018 0.047998 1.06746621 0.75143811
0.000015 0.052205 2.21027928 0.68007404
0.000016 0.057457 1.47667452 0.83393107
0.000016 0.056249 2.62565862 1.26190596
0.000016 0.061392 2.71878543 1.01751283
0.000017 0.047199 1.39021429 1.14600119
0.000016 0.051444 1.94558414 1.71127878
0.000017 0.049175 1.46224371 0.98020747
0.000017 0.049095 3.31138490 0.76387218
0.000015 0.047646 1.74084605 1.00064168
0.000015 0.049683 2.27498510 1.05551031
3.2 Transient Heat Flow
Our goal is to calculate the Temperature after t
seconds when we consider the heat problem
Figure 4: 1D Transient Heat problem.
The parabolic partial differential equation can describe the
transient heat flow in the simplest way we get:
1
The boundaries conditions
,0,
,
,,
2
,,0
,
,,
The initial conditions
0,,
0,,
The ANN training data is generated by find the
analytic solution (variable separations. Two more
numerical solution is obtained from finite difference
Crank–Nicolson method and implicit scheme.
Figure 5: ANN default model.
The ANN using MATLAB Feedforward neural
network with network training function that updates
weight and bias values according to Levenberg-
Marquardt optimization. The result shows
significant errors especially when the nonlinearity
appears
Figure 6: Transient Flow: - ANN vs Analytic result.
And the error graph
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
336

Figure 7: Transient flow: - Errors percentage.
To investigate the geometrical boundaries effects we
add new input to the ANN model and train in the
same previous conditions.
Figure 8: ANN model with geometrical boundaries inputs.
The results change with much less error percentage
Figure 9: Transient & geometrical: - ANN vs Analytic.
Figure 10: the errors with geometrical boundaries input.
The performance analysis wan not execute yet.
4 CONCLUSIONS
A novel ANN approached to simulate the fluid
behaviour was proposed. We successfully manage to
get acceptable results for heat transfer model both
the steady state and transient.
Our ANN approach is fast, simple and efficient
for fluid heat flow prediction. We able to investigate
the effect of the geometry with known boundaries
velocity. Our outcomes are acceptable for 1D-flow
equations with respect to both energy and
momentum equations. The ANN approach is able to
handle fluid flow prediction with known boundaries
velocity. This approach can be the first step for
neural network computational program that can
tackle variance type of problems.
ACKNOWLEDGEMENTS
The authors would like to acknowledge flow
assurance group in Universiti Teknologi PETRONS
for their supports.
REFERENCES
Islamoglu, Y., A. Kurt, and C. Parmaksizoglu,
Performance prediction for non-adiabatic capillary
tube suction line heat exchanger: an artificial neural
network approach. Energy Conversion and
Management, 2005. 46(2): p. 223-232.
ANewArtificialNeuralNetworkApproachforFluidFlowSimulations
337

Liu, T., et al., Neural network analysis of boiling heat
transfer enhancement using additives. International
Journal of Heat and Mass Transfer, 2002. 45(25): p.
5083-5089.
Dı
́
az, G., et al., Dynamic prediction and control of heat
exchangers using artificial neural networks.
International Journal of Heat and Mass Transfer,
2001. 44(9): p. 1671-1679.
Rajkumar, T., & Bardina, J. (2003). Training data
requirement for a neural network to predict
aerodynamic coefficients. In Proceedings of 17 th
Annual International Symposium on Aerospace/
Defense Sensing, Simulation and Controls. Orlando,
EUA.
Panigrahi, P., et al., Prediction of turbulence statistics
behind a square cylinder using neural networks and
fuzzy logic. Journal of fluids engineering, 2003.
125(2): p. 385-387.
Benning, R.M., T.M. Becker, and A. Delgado, Initial
studies of predicting flow fields with an ANN hybrid.
Advances in Engineering Software, 2001. 32(12): p.
895-901.
Benning, R.M., T.M. Becker, and A. Delgado, Principal
Feasability Studies Using Neuro - Numerics for
Prediction of Flow Fields. Neural Process. Lett.,
2002. 16(1): p. 1-15.
Hirschen, K. and M. Schäfer, Bayesian regularization
neural networks for optimizing fluid flow processes.
Computer Methods in Applied Mechanics and
Engineering, 2006. 195(7–8): p. 481-500.
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
338
