Self Recommendation in Peer to Peer Systems

Agostino Forestiero

Institute for High Performance Computing and Networking, ICAR-CNR,

Via Pietro Bucci, 41C, 87036 Rende (CS), Italy

Keywords:

Recommendation systems, Peer to Peer.

Abstract:

Recommendation system aims to produce a set of signiﬁcant and useful suggestions that can be meaningful

for a particular user. This paper introduces a self-organizing algorithm that by exploiting of a decentralized

strategy builds a distributed recommendation system. The available resources are represented by a string of

bits namely describer. The describers are obtained by exploiting of a locality preserving hash function that

maps similar resources into similar strings of bits. Each pear works independently with the aim to locate the

similar describer in neighbor peers. The peer decisions are based on the application of ad-hoc probability

functions. The outcome will be a fast recommendation service thanks to the emergent sorted overlay-network.

Preliminaries experimental results show as the logical reorganization can improve the recommendation oper-

ations.

1 INTRODUCTION

The task of recommendation systems is to create a list

of interesting items for the users when it has to make

a choose in a given contest. In other words, it use the

past opinions e/o the behaviors of whole community

to help the users of the same community to more ef-

ﬁciently make a new choice. These systems can be

built for movies, books, communities, news, articles

etc. Recommendation systems have become an im-

portant research topic and much work have been pro-

posed both in the industry and academia on develop-

ing new approaches in this ﬁeld. The companies col-

lect a large amount of transactional data that allows a

careful analysis of how an user interacts with the set

of available choices. This can be a way to automa-

tize the generation of recommendations based on data

analysis. The way used to analyze the data and de-

velop the concepts of afﬁnity between users and items

distinguishes the recommendation systems.

The usefulness of an item or product is generally

represented by a rating, which indicates how a given

user liked a particular item. The items or products

having an high value of rate are presented as recom-

mendations for the user. The recommendation sys-

tems can be categorized as (Balabanovi´c and Shoham,

1997): (i) Collaborative Filtering (CF) where an item

or product is recommended to the user according to

the past ratings of all users, i.e. systems are based

on historical interactions; (ii) Content-based recom-

mending where the item or product is recommended if

it is similar in content to items or products the user has

chosen in the past, or matched with given attributes

of the user; (iii) Hybrid approaches in which collab-

orative and content-based approaches are combined.

In collaborative ﬁltering approach – the term was in-

troduced in ﬁrst commercial recommendation system

known as Tapestry (Goldberg et al., 1992) – the util-

ity of the item i for the user u is estimated based on

the utilities assigned to item i by those users v who

are “similar” to user u. Practically, this kind of sys-

tem try to predict the utility of items for a given user

based on the items previously rated by other similar

users. For example, in a music recommendation sys-

tem, to recommend music to user u, the collaborative

system ﬁnds the “similar” of user u, i.e., other users

that have similar tastes in music. Then, the music that

are liked by the similar of user u would be recom-

mended. To compute the similarity between two users

have been used various approaches, where, often, the

similarity is based on their ratings of items that both

users have rated. The most popular are correlation and

cosine similarity. In the correlation-based approach,

the Pearson correlation coefﬁcient is used to compute

the similarity (Resnick et al., 1994), (Shardanand and

Maes, 1995):

simlarity(u, v) =

∑

iεI

u,i

− ¯r

)(r

v,i

− ¯r

)

∑

iεI

u,i

− ¯r

)

∑

iεI

v,i

− ¯r

)

where I is the set of all items rated by both users u

332

Forestiero A..

Self Recommendation in Peer to Peer Systems.

DOI: 10.5220/0005157603320336

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 332-336

ISBN: 978-989-758-052-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

and v. The value of the rating r for user u and item i is

computed as an aggregate of the ratings of some other

users for the same item i. The cosine-based approach

(Breese et al., 1998), (Sarwar et al., 2001), uses two

vectors in n-dimensional space to represent the users

u and v, and n will be |I|. The cosine of the angle

between two vectors can be computing to measure the

similarity between them:

similarity(u, v) = cos(

−→

u ,

−→

v ) =

−→

u ·

−→

u |

× |

−→

v |

∑

iεI

u,i

v,i

∑

iεI

u,i

∑

iεI

u,i

where

−→

u ·

−→

v indicates the dot-product between

the vectors

−→

u and

−→

v .

Content-based recommenders provide recommen-

dations by comparing representations of content that

interests the user to representations of content de-

scribing an item. Recommended items have associ-

ated textual content, such as books, web pages, and

movies. The web pages should be associated to con-

tents like descriptions and user reviews. Information

retrieval (IR) technics address this problem, where the

content associated can be handled as a query, and the

unrated documents marked with a similarity value to

this query (Balabanovi´c and Shoham, 1997). Other-

wise, the documents can be converted into word vec-

tors, and then averaged to obtain a prototype vector of

each category for a user, as showed in (Lang, 1995).

Collaborative and content-based approaches use

the same cosine measure from information retrieval.

But, in content-based recommendation systems mea-

sures the similarity between vectors of weights,

whereas, in collaborative systems measures the sim-

ilarity between vectors of the actual ratings speciﬁed

of the users. Other approaches to the recommendation

consist in handling of the problem as a classiﬁcation

task. Each pattern represents the content of an item,

and a user’s past ratings are used as labels for these

patterns. For example, text from ﬁelds such as title,

author, synopses, reviews, and subject terms are used

by (Mooney and Roy, 2000) to recommend books.

Several classiﬁcation algorithms have been used to

content-based recommend: decision trees, k-nearest

neighbor, and neural networks (Pazzani and Billsus,

1997).

In this paper, a self organizingalgorithm for build-

ing a peer to peer recommendation system, is pro-

posed. The algorithm is able to distribute and cleverly

organize the “descriptor of resources” in order to im-

prove discovery operations. In peer to peer systems,

bit vectors or keys, are often exploited to describe the

resources and with different meanings. The presence

or absence of a given topic can be represented thor-

ough a bit (Crespo and Garcia-Molina, 2002)(Platzer

and Dustdar, 2005). With resource like documents,

it is particularly appropriate, because it is possible

to recognize the topics. An hash function was em-

ployed to map the resources with strings of bits in

(Cai et al., 2004) (Oppenheimer et al., 2005). With an

hash function locality preserving, similar describers

are assigned to similar resources and then placed in

the same region of the network. Thus, it is very prob-

able ﬁnd similar and appreciated describers close to

the target describer (recommendations). In the rest

of the paper a preliminary version of the algorithm

is introduced in section 2 and an initial experimental

analysis is showed in section 3.

2 SELF ORGANIZING

RECOMMENDATION SYSTEM

In this section a distributed self-organizing algorithm

for building a recommendation system, is introduced.

The aim of the algorithm is to logically reorganize

the describers that describe the available and recom-

mendable resources to allow recommendation opera-

tions faster. The algorithm cleverly disseminates the

describers on the network with the aim of spatially

sort them. Thanks to this spatial reorganization, sim-

ilar describers, representing similar resources, will be

placed in neighbor hosts. A set of similar describers

representing similar resources can be detected in the

neighborhood of the target resource and suggested to

the user. The sorting process is progressivelyand con-

tinuously realized by each peer achieving simple and

local operations. Probability functions steer the op-

erations of sending and depositing of the describers.

These simple operations are performed in local and a

sort of global intelligence emerges from work of un-

aware peers. Two probability functions, P

send

to eval-

uate the probability to send the describers, and P

deposit

to evaluate the probability to deposit the describers,

are employed. The probability functions derive from

the formulas exploited by biological systems for self-

organizing their behavior (Lumer and Faieta, 1994).

In this systems, unaware entities independently and

locally work in order to produce a global intelligent

behavior.

Each peer evaluates the probability function P

send

for each stored describer, so as to decide whether or

not to gather describers and send them to a neighbor

peer; the probability function P

deposit

is evaluated by a

peer when a set of describers arrives from a neighbor

peer. Peer’ decisions, i.e. probability functions, are

based on a similarity function that measures the aver-

age similarity of a describer des with all the describers

located in the local region. All the hosts reachable

SelfRecommendationinPeertoPeerSystems

333

from the current host with a given number of hops

represent the local region. Here, the similarity func-

tion S for the describer

des in local Region is reported

in formula(1):

S =

∑

desεRegion



1−

1− cos(des,

des)



(1)

where, N is the overall number of describers in the

Region, N

is the number of describers maintained in

each host, while cos(des,

des) is the cosine distance

between des and

des. The parameter α is the sim-

ilarity scale and here it is set to 2. The value of S

assumes values ranging between -1 and 1, but nega-

tive values are ﬁxed to 0. The bulk of describers is

propagated across the network until all describers are

dropped. Each peer that receives the set of describers

from a neighbour evaluates the P

deposit

function for

each describer and in case take it. The probability to

send a describer must be inversely proportional to the

similarity of this describer with those located in the

visibility region, so that dissimilar describer are sent

away of the region. When similar describer being to

be accumulated the initial equilibrium is broken and

a reorganization of describers is increasingly driven.

The probability function to gather for sending a de-

scriber is deﬁned in formula(2):

send



k1+ S



(2)

the parameter k1, whose value is comprised be-

tween 0 and 1, can be tuned to modulate the de-

gree of similarity. Here k1 is set to 0.1 (Bonabeau

et al., 1999). The local region accumulates similar de-

scribers because the dissimilar describers will be sent

away.

Whenever a bulk of describers gets to a new host,

the probability function P

deposit

,is evaluated. It is di-

rectly proportional to the similarity function S , i.e.,

to the average similarity of this describer with the de-

scribers maintained in the current visibility region.

deposit



k2+ S



(3)

the parameter k2 is set to 0.5 (Bonabeau et al.,

1999).

An algorithm for exploiting the logical reorgani-

zation and then obtain a set of describers representing

resource that can be suggested, is very simple and im-

mediate. A query will be issued by an host (user) to

search a target describer representing the wished re-

source and it will be forwarded through the peer to

peer network to collect as many target describers as

possible. Thanks to the logical reorganization a, the

queries can be forwarded towards the host with the

maximum value of similarity between representative

describer and the target describer. The representative

describer is a virtual describer, for each host, built by

averaging of the values of all describers located in a

current host. When a query is issued by an host for a

target resource, a virtual target describer is created.

The query will be forwarded towards the neighbor

peer with the maximum value of similarity, based on

formula 1, between the virtual target describer of the

query and the representativedescriber of the host. The

same operation will be done by each host that received

a query and has to forward it to one of its neighbors.

When the query gets to an host with a representative

describer equal to the virtual target describer, or the

maximum number of query hops admissible is ﬁn-

ished, the query will be directly forwarded to the host

that has issued the request. The query going across

the network collects a set of describers similar to the

virtual target describer, which can be exploited to pro-

duce a list of suggestion/recommendation to the user.

The discovery algorithm is very simple and needs

very little computing and memory resources, it is very

efﬁcient as it exploits the continuous work of the al-

gorithm that organize the describers.

3 EXPERIMENTAL RESULTS

An event-based simulator was implemented to evalu-

ate the performance of the algorithm. A P2P network

with number of hosts equal to 2,500 was considered

where each peer is linked to 4 hosts on average. The

number of resources published by each host is equal

to 15 on average and indexed with a preﬁxed string of

bits obtained using a locality preserving hash function

to guarantee that describer give similar keys. Exploit-

ing the algorithm of Albert and Barabasi (Barab´asi

and Albert, 1999)a scale free topology network was

built. In this way, the characteristics of real networks

are careful considered. A graphical description of the

logical reorganization is reported in Figure 1. Here,

each describer is associated to a color. A part of the

network is photographed: (a) at Time = 0 sec, when

the process is starting and the describers are randomly

distributed and (b) at Time = 50,000 time units when

the process is in a steady situation. Notice that similar

describers are located in the same region and between

near region the color change gradually, which proves

the spatial sorting on the network.

The trafﬁc generated by the process of reorgani-

zation, that is the average number of bulks per sec-

ond that are processed by an host, does not depend

neither on the network size nor on the churn rate. It

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

334

Figure 1: Snapshots of a part of the network when the pro-

cess is starting (a), and when the process is in a steady situ-

ation (b).

only depends on the number of forwarding and their

frequency across the network. In simulated scenario,

each server processes about one send/deposit opera-

tion every 20 time units, which can be considered an

acceptable load for the host. The trafﬁc, that is the

number of operations that a host elaborates per time

units, was calculated and shown in Figure 2. We can

see as the value of the trafﬁc changes according to the

value of maximum number of hops done within a sin-

gle sending. In this ﬁgure the distance of the neighbor

target peer, i.e. the number of hops achieved by bulks

before the host evaluates the probability function, was

varied. It was noted that the reorganization process

is accelerated if distance of jump are longer, because

they can scan the network more quickly. The max-

imum number of hops is a compromise between the

trafﬁc load tolerable and the rapidity and efﬁciency of

the reorganization. It was possible to note during the

simulations that the processing load does not depend

on system parameters such as the average number of

0.01

0.02

0.03

0.04

0.05

0 20,000 40,000 60,000 80,000 100,000

Traffic

Time units

jump.length = 1

jump.length = 3

jump.length = 5

jump.length = 7

Figure 2: The trafﬁc generated by the algorithm when the

number of hops of each sending ranges from 1 to 7.

resources handled by a host or the number of hosts,

which is a conﬁrmation of the scalability properties

of the algorithm.

A spatial index of Similarity rate was deﬁned to

evaluate the goodness of the algorithm. For each peer,

the similarity among all the local describer within the

local region, by averaging the cosine of the angle be-

tween every couple of describers, was calculated. The

values of the Similarity rate has been averaged for all

the hosts of the network. Our aim is to increase the

Similarity rate value as more as possible. It would

mean that similar describers are located into neigh-

bor hosts and an effective sorting of describer is be-

coming. In Figure 3 the Similarity rate of the whole

0.45

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0 20,000 40,000 60,000 80,000 100,000

Similarity rate

Time units

describer.length = 3

describer.length = 4

describer.length = 5

describer.length = 6

Figure 3: Similarity rate of the whole network when the

length of bit strings ranges from 3 to 6.

network when the length of describer bit strings that

represent the resources, is varied. It is possible to

note how the logical reorganization is achieved inde-

pendently of the length of bit strings. The scalability

of the algorithm is conﬁrmed analyzing its behavior

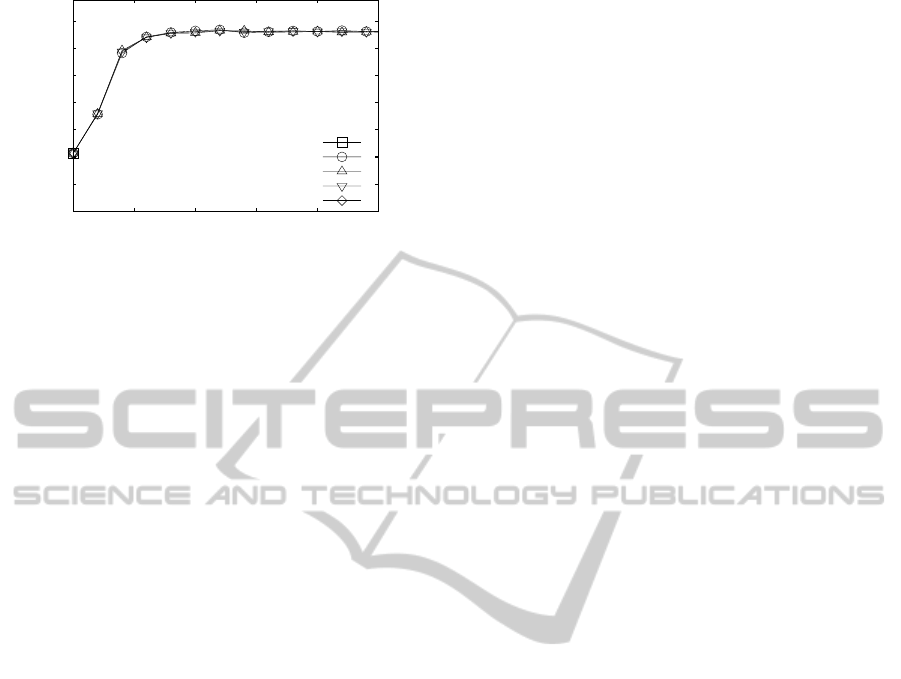
when the network size is varied. Figure 4 reports the

values of Similarity rate when the network size ranges

from 1,000 to 16,000 hosts. Notice that the number of

the involvedhosts in the logical reorganization,has no

SelfRecommendationinPeertoPeerSystems

335

0.4

0.45

0.5

0.55

0.6

0.65

0.7

0.75

0 20,000 40,000 60,000 80,000 100,000

Similarity rate

Time units

net.size = 1,000

net.size = 2,000

net.size = 4,000

net.size = 8,000

net.size = 16,000

Figure 4: Similarity rate of the whole network when the

network size ranges from 1,000 to 16,000 hosts.

detectable effect on the Similarity rate value.

4 CONCLUSION

A self-organizing algorithm to build a distributed rec-

ommendation system, was introduced. The available

and recommendable resources in a network are de-

scribed by means describer and logically reorganized.

The describer are arranged as bit strings obtained by

the application of a locality preserving hash func-

tion that allows to map similar resources into similar

strings. Hosts autonomously send/deposit describer

exploiting probability functions. Preliminary exper-

imental results showed as the algorithm achieves an

effective reorganization of descriptors. The emerging

logical overlay allows to improve discovery and rec-

ommendation operations.

REFERENCES

Balabanovi´c, M. and Shoham, Y. (1997). Fab: content-

based, collaborative recommendation. Communica-

tions of the ACM, 40(3):66–72.

Barab´asi, A.-L. and Albert, R. (1999). Emergence of scal-

ing in random networks. science, 286(5439):509–512.

Bonabeau, E., Dorigo, M., and Theraulaz, G. (1999).

Swarm intelligence: from natural to artiﬁcial systems,

volume 4. Oxford university press New York.

Breese, J. S., Heckerman, D., and Kadie, C. (1998). Empir-

ical analysis of predictive algorithms for collaborative

ﬁltering. In Proceedings of the Fourteenth conference

on Uncertainty in artiﬁcial intelligence, pages 43–52.

Morgan Kaufmann Publishers Inc.

Cai, M., Frank, M., Chen, J., and Szekely, P. (2004). Maan:

A multi-attribute addressable network for grid infor-

mation services. Journal of Grid Computing, 2(1):3–

14.

Crespo, A. and Garcia-Molina, H. (2002). Routing indices

for peer-to-peer systems. In Distributed Computing

Systems, 2002. Proceedings. 22nd International Con-

ference on, pages 23–32. IEEE.

Goldberg, D., Nichols, D., Oki, B. M., and Terry, D. (1992).

Using collaborative ﬁltering to weave an information

tapestry. Communications of the ACM, 35(12):61–70.

Lang, K. (1995). Newsweeder: Learning to ﬁlter netnews.

In In Proceedings of the Twelfth International Confer-

ence on Machine Learning, pages 331–339. Citeseer.

Lumer, E. D. and Faieta, B. (1994). Diversity and adapta-

tion in populations of clustering ants. In Proceedings

of the Third International Conference on Simulation

of Adaptive Behavior : From Animals to Animats 3:

From Animals to Animats 3, SAB94, pages 501–508.

MIT Press.

Mooney, R. J. and Roy, L. (2000). Content-based book rec-

ommending using learning for text categorization. In

Proceedings of the ﬁfth ACM conference on Digital li-

braries, pages 195–204. ACM.

Oppenheimer, D., Albrecht, J., Patterson, D., and Vahdat,

A. (2005). Design and implementation tradeoffs for

wide-area resource discovery. In High Performance

Distributed Computing, 2005. HPDC-14. Proceed-

ings. 14th IEEE International Symposium on, pages

113–124. IEEE.

Pazzani, M. and Billsus, D. (1997). Learning and revis-

ing user proﬁles: The identiﬁcation of interesting web

sites. Machine learning, 27(3):313–331.

Platzer, C. and Dustdar, S. (2005). A vector space search en-

gine for web services. In Web Services, 2005. ECOWS

2005. Third IEEE European Conference on, pages 9–

pp. IEEE.

Resnick, P., Iacovou, N., Suchak, M., Bergstrom, P., and

Riedl, J. (1994). Grouplens: an open architecture for

collaborative ﬁltering of netnews. In Proceedings of

the 1994 ACM conference on Computer supported co-

operative work, pages 175–186. ACM.

Sarwar, B., Karypis, G., Konstan, J., and Riedl, J. (2001).

Item-based collaborative ﬁltering recommendation al-

gorithms. In Proceedings of the 10th international

conference on World Wide Web, pages 285–295.

ACM.

Shardanand, U. and Maes, P. (1995). Social information

ﬁltering: algorithms for automating word of mouth.

In Proceedings of the SIGCHI conference on Human

factors in computing systems, pages 210–217. ACM

Press/Addison-Wesley Publishing Co.

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

336