A Discrete Event Simulation Model to Support Bed Management

Paolo Landa

1,2

, Michele Sonnessa

, Elena Tànfani

and Angela Testi

Department of Economics and Business studies, University of Genoa, Via Vivaldi 5, Genoa, Italy

Agenzia Regionale Sanitaria Liguria, Genova, Italy

Keywords: Health Care Services, Bed Management, Discrete-Event Simulation.

Abstract: In recent years, due to the overcrowding of Emergency Department (ED) and the growing concern in

reducing the number of inpatient ward beds, it has become crucial to improve the capacity planning and

control activities, which manage the patient flows from EDs to hospital wards. Bed Management has a key

role in this context. This study starts by a collaboration with the Local Health Government (LHG) of the

Liguria region aimed at studying the impact of supporting bed management with some operational strategies

without increasing the bed capacity. A large amount of data was collected over a one-year period at public

hospital in Genova and a preliminary observational analysis was conducted to get the main information

about the flow of emergency and elective patients from ED to inpatient wards. A Discrete Event Simulation

(DES) model has been then developed in order to represent the real system. A scenarios analysis is proposed

to assess the best strategy to improve the system performance without increasing bed capacity, by simply

synchronizing bed supply and demand. The model can be used as a decision support tool to optimise the use

of the available resources as well as to improve the quality of the patient pathway inside the hospital.

1 INTRODUCTION AND

PROBLEM ADRESSED

In recent years, in order to increase clinical

outcomes and citizens’ satisfaction, there has been a

growing concern to reduce overcrowding in

Emergency Department (ED). Two main

interventions are usually suggested (Bagust et al,

1999). Firstly, reducing the number of patients

which inappropriately addressees the EDs. Secondly,

facilitating early discharges from inpatient wards to

facilitate on time emergent admissions in inpatient

departments.

In Italy, regional decision makers tackled the

first intervention encouraging general practitioners

to give appropriate pathways for their patients, by

giving more non-hospital options available and

imposing a co-payment for non-appropriate

admissions. Indeed in one year access to ED has

been reduced by about 1 million (Agenas, 2012). In

spite of that, EDs are always overcrowded. This is

mainly due to both a public budget unbalance and

the reduction, in the same period, of the number of

inpatient ward beds available, which has been

reduced drastically, from 6.1 to 4.3 per thousand

population in ten years ranking below the European

average (Istat, 2011).

Nowadays hospitals are focusing on the second

intervention trying to facilitate early discharges from

inpatient beds and get more beds available for

emergent patients to be admitted. This entails to

recognize that the so-called “ED problem,” is

actually a “system problem”. ED is simply a step in

the patient flow through the hospital and increasing

capacity in the ED without facilitating a smooth exit,

can worsen the problem (IHI, 2003). In the past the

problem has been already addressed extensively in

many health systems, mainly North American and

UK (Audit Commission, 1992; Audit Commission,

1993; IHI, 2003). A solution suggested is the

introduction of the so-called Bed Manager (BM). It's

main task is to report at given interval time slots

during the day the volume, census, and occupancy

rates of the available ward stay beds in order to

synchronize the expected discharges, i.e. bed supply,

with the expected admissions from ED, i.e. bed

demand, (Haraden et al., 2004).

The BM is not a new concept. Indeed, twenty

years ago, it has already been defined as the way of

“keeping a balance between flexibility for admitting

emergency patients and high bed occupancy, which

901

Landa P., Sonnessa M., Tànfani E. and Testi A..

A Discrete Event Simulation Model to Support Bed Management.

DOI: 10.5220/0005161809010912

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (HA-2014), pages

901-912

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

is an indicator of good hospital management” (Green

and Armstrong, 1994).

The bed manager function has been proved to be

effective. For instance, Howell et al. (2008) report

an increase of the ED throughput, substantially due

to the reduction of about 25% (approximately one

hour and half) of the time spent inside ED. This

effect was still larger in transferring patients from

ED to Intensive Care Units (Howell et al., 2010).

Efficient patient throughput, however, requires a

high degree of coordination and communication

among the different staff and health care facilities

involved. The control of the whole set of patient

flows, is obviously possible only with the help of an

on-line system able to identify earlier information

about pending admissions to the acute beds available

(Tortorella et al., 2013). This can be done, for

instance, visualizing the on time patient flows by

means of a tool which collects and filters the

information from the ED and inpatient ward thus

supporting hospital bed managers in their daily

decision making (Jensen et al., 2012).

Of course BM should be supplemented by other

techniques generally intended to reduce the patient

flows variability inside the hospital, developing all

activities and tools to allow supply matching

demand in a dynamic situation. Many operations

research and management science methods such as

queuing theory, supply chain models, optimization

and simulation, can be used study this problem. In

fact, the analysis of patient flows and clinical

pathways are a key issue in the recent operational

research literature (see, for instance, Vanberkel et al,

2009; Vissers et al., 2005). In addition, many other

methods from industrial and business process

modelling have been also used, such as lean health

care or six sigma (Young et al., 2004).

Health Foundation (2013) provides an extensive

collection of empirical research studies aimed at

improving patient flow across pathways, not only

through BM. From the analysis of the literature it

appears that the scope, responsibility and role of bed

manager is not clearly defined and it is actually

rather different in practical applications: medical,

nursing or managerial staff can perform the bed

manager function and even tasks or levels may be

different (Proudlove et al., 2007). The non-existence

of standards of bed management practice is taken to

reflect a lack of systematic attention paid to this role

(Boaden et al, 1999). In the operative scenario of the

Italian Health System herein studied, the bed

management has been only recently introduced in

hospitals and no systematic results are until now

available (Simeu, 2011).

This study starts by a collaboration with the

Local Health Government (LHG) of the Liguria

region aimed at studying the impact of supporting

bed management with some operational strategies

without increasing the bed capacity. At least to the

authors knowledge, this is the first attempt to give

some quantitative insights in this field.

The specific objective of this paper is to develop

a Discrete Event Simulation (DES) model to study

the interrelation of the flows of emergent and

elective admissions into inpatient departments and

show how the model can help in supporting the bed

management decisions. The advantage to use a DES

model is mainly related to its ability to give a deep

analysis of the dynamic flows of patients throughout

different time windows. It is not sufficient to

consider the average distribution pattern. Capacity

and demand may match on average, and it may look

as though the system ought to flow smoothly.

However, even when capacity and demand match on

average, the degree of variation in the timing of the

patient arrivals (demand) and the ability of beds to

absorb that demand can results in admission delays

and cancellations.

Simulation has been already utilized in bed

management literature. Bagust (1999) applies a

stochastic simulation model to determine which is

the optimal level of spare capacity in presence of

flows by their nature stochastic and difficult to

predict, resulting in 85% bed occupancy at most.

Harper et al. (2002) utilize a DES model not only to

manage but also to plan the bed capacity, with

particular regard to the trade-off between bed

occupancy and refusals. Schmidt et al. (2013)

implement a DES model to assess a decision support

system for bed management in a context where there

is inherent uncertainty in length of stay and ED

patients to be admitted.

In this paper, we focus on studying the flow

variability in order to manage the on-line decisions

to be taken at a given set of time windows. The

effect of different BM rules is evaluated by means of

a set of performance indexes. They are chosen to

take into consideration both the hospital point of

view (bed occupancy, turnover interval, additional

beds) and the patient point of view (misallocation,

cancellations of elective admissions already

scheduled, excessive waits). The BM rule are

defined assuming a flow process where emergent

patients are “pushed” through the system from the

ED to the acute wards and “pulled” towards

anticipated discharge (Proudlove et al., 2003).

The paper is organized as follow. In Section 2 the

description of the simulation model structure and

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

902

performance metrics to be used for the analysis are

given. In Section 3 the case study is introduced

together with the data collection and analysis

performed with the collaboration of the Local Health

Government (LHG) of the Liguria region. Section 4

is devoted to the model validation and experiment

settings, while in Section 5 the preliminary results of

the scenarios analysis tests are given. Conclusions

and future direction of the research end the paper.

2 SIMULATION MODEL

DESCRIPTION

The main aim of the model herein developed is to

study the interrelation and synchronization of the

patient flows between an emergency department and

a set of inpatient hospital wards. A discrete-event

simulation model has been developed adopting a

patient-centred approach. From an operational point

of view, this means considering the patient

characteristics regarding their clinical need (medical,

surgical, orthopaedics or others) and the timing of

the care process from their entrance into the system

until their exit.

The overview of the system under study, main

elements and patient flows involved is reported in

Figure 1.

Both emergent and elective patients flow across

the system made up of one ED and a given set of

hospital inpatients wards.

Hospital wards are divided into a set of n groups

(in the case study reported in Section 3 they are:

medical, surgery, orthopaedic and other wards).

Emergent patients exiting from the ED with a

decision to admit and the elective ones compete for

the same beds available in the wards. The elective

patients are previously registered in a waiting list

and the date of admissions is fixed a priori. This

means that this flow can be controlled and indeed

this can be a way to smooth the demand for beds.

Obviously, emergent patients can be admitted into a

ward if and only if there is a free bed available. Note

that for both emergent and elective patient arrivals, a

detailed shift pattern is created to simulate the

different arrival distribution during the day and

week. For each emergent patient who arrives in the

system four attributes are generated. The attribute

“to_admit” can assume the value 1 or 0, if

respectively, the patient must be admitted into an

hospital ward and 0 if is discharged. The Attribute

“ward” gives the ward where the patients to be

admitted should be allocated. The “Time_in_ED” is

the time spent by the patient within the ED. These

attributes are generated with different distributions

depending on the slot time of arrival. Besides, for

both elective patients and emergent to be admitted,

the Length of Stay (LOS) is also generated with a

different pattern depending on the type of patient

(emergent or elective) and the ward they are

assigned to. When the elective patients have spent in

the emergency department their “Time_in_ED”,

they become ready and are then processed by a

machine which verifies if they must be admitted into

a hospital ward or not. In the positive case they are

pushed into one of the buffers “To_be_admitted”

depending on the ward they are assigned to.

Afterwards at a priori determined time windows

during each day the “bed manager”, verifies the

consistency of available ward beds and decides the

emergent patients allocation to them. The number of

beds available in each ward is known as well as the

average number of elective arrivals during the

following time slots in the same day as well as the

transferrals of patients among inpatient wards. After

the admission the patients stay in the inpatient ward

accordingly to the assigned “LOS” attribute.

Different rules and levels of timing and look

ahead policies can be applied to simulate the bed

manager decisions. The set of performance metrics

used to test and compare the impact of different BM

rules and hospital ward organizational strategies is

reported in the next section, while the preliminary

results of the scenario analysis performed are given

in Section 5.

2.1 Performance Metrics

The impact of applying alternative bed management

rules is assessed by means of the following main

indicators:

1. Misallocation index: percentage of patients

admitted in a ward different from the one assigned to

them at the ED decision to admit. In a baseline

scenario patients can be placed in the first available

bed, but this is not always appropriate. It is

important, for instance, to limit the number of

medical ward beds occupied by surgical patients

and, vice versa. (Audit commission, 1993).

2. Average number of patients waiting to be

admitted for each ward, time slot/day (additional

beds or trolley in ED)

3. Waiting times before admission for emergent

patients into inpatient wards. Note that national

guidelines give a maximum time of 4 hours for UK

Proudlove et al., 2003) and 8 hours in Italy (Simeu,

2011).

ADiscreteEventSimulationModeltoSupportBedManagement

903

Figure 1: Overview of the system and flows of patients under study.

4. Number of elective patients postponed for the

unavailability of a free bed in the day a priori fixed

for their admission .

5. Bed utilization rate: bed occupancy of stay beds

for each ward (total, emergent and elective ones).

3 CASE STUDY

Our case study refers to a large hospital in the city of

Genova. The data has been provided by the Local

Health Government of Liguria (Agenzia Regionale

Sanitaria). In 2012, the number of patients arrivals at

the ED was 84,781. As shown in Table 1,

approximately one out of four (24.7%), i.e. 20,942,

were subsequently admitted to an inpatient ward. In

the same period 24,696 elective patients were

admitted into the same wards.

The total number of beds available in the wards

is 1256, distributed among 79 wards. The wards

have been grouped into four main groups, i.e.

Medicine, Surgery, Orthopaedics and other wards,

respectively. For each ward group the number of

beds available, the average time spent in the ED and

the average length of stay are reported.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

904

Table 1: Case study descriptive analysis.

# of ED admissions

84,781

% discharged without admissions (75.3%)

% transferred to inpatient wards (24.7%)

# of inpatient ward admission

45,638

elective 24,696

coming from ED 20,942

Average time spent in ED (in hours)

patients discharged without admission 2.92

patients transferred to inpatient wards 4.45

Average LOS (in days)

Medicine 3.14

Surgery 6.87

Orthopaedics 9.00

Other 8.73

# of ward beds

1,141

Medicine 332

Surgery 157

Orthopaedics 80

Other 569

3.1 Data Collection and Analysis

During a one year period, January 2012- December

2012, data have been collected from two database

sources which refer to the flow of patient within the

emergency department and hospital wards,

respectively. From the first, we get the day and time

of arrival and the exit decision from the ED (to be

admitted into an hospital ward or not). From the

second, we collected for both elective and emergent

patients the date and time of admission; the ward of

admission, the eventual transferral information to

other wards and the date and time of discharge from

the hospital.

A deepest analysis has been devoted to estimate

the inter-arrival and service rates for both emergent

and elective patients. They are, apparently, very

variables. Indeed, there is a large difference in

arrivals between weekdays and weekends, working

and resting time. Their variance, however, can be

reduced when particular time slots are considered.

Therefore, with the help of the medical staff 42 time

slots have been chosen to cover each week time

period (Table 2).

For each emergent patient the value of the

attribute “ward” has been generated using the

empirical distribution reported in Table 3.

In Figure 2 the overall trend of patient flows

during the 42 slots time is given. In particular, for

each timeslot the number of patient discharged and

Table 2: Time slots and shift pattern.

Slot Day Time Slot Day Time

1 Mon 0-7 22 Thurs 13-16

2 Mon 7-10 23 Thurs 16-19

3 Mon 10-13 24 Thurs 19-24

4 Mon 13-16 25 Fri 0-7

5 Mon 16-19 26 Fri 7-10

6 Mon 19-24 27 Fri 10-13

7 Tues 0-7 28 Fri 13-16

8 Tues 7-10 29 Fri 16-19

9 Tues 10-13 30 Fri 19-24

10 Tues 13-16 31 Sat 0-7

11 Tues 16-19 32 Sat 7-10

12 Tues 19-24 33 Sat 10-13

13 Wed. 0-7 34 Sat 13-16

14 Wed. 7-10 35 Sat 16-19

15 Wed. 10-13 36 Sat 19-24

16 Wed. 13-16 37 Sun 0-7

17 Wed. 16-19 38 Sun 7-10

18 Wed. 19-24 39 Sun 10-13

19 Thurs 7-10 40 Sun 13-16

20 Thurs 10-13 41 Sun 16-19

21 Thurs 13-16 42 Sun 19-24

Table 3: Emergent patients ward admissions.

Ward Group %

Medicine 62.47

Surgery 4,80

Orthopaedics 5,93

Other 26,80

admitted is given. The number of patients admitted

is also splitinto emergency and elective flows.

These flows represent for each slot the supply of

beds, which consists of the patients discharged that

are leaving a bed free for a new admission, and the

demand for ward beds, composed by emergent

patients to be admitted from the ED and elective

patients already scheduled to be admitted into

inpatient wards.

A grayed area also highlights the internal flow of

patient transferred from one ward to another. It does

not affect the admission/discharges flows but has a

significant impact over ward occupancy rates. Two

main remarks can be outlined. The most of the

discharges are concentrated in the days before the

weekend, while the admissions are mainly

concentrated in the first days of the week. This

effect is mainly due to the internal hospital

organization and can have great impact over the bed

occupancy flows and allocation. Looking at the

internal distribution of arrival flows it is clear how

the elective patients are admitted on regular

frequency, mostly at the beginning of the week,

ADiscreteEventSimulationModeltoSupportBedManagement

905

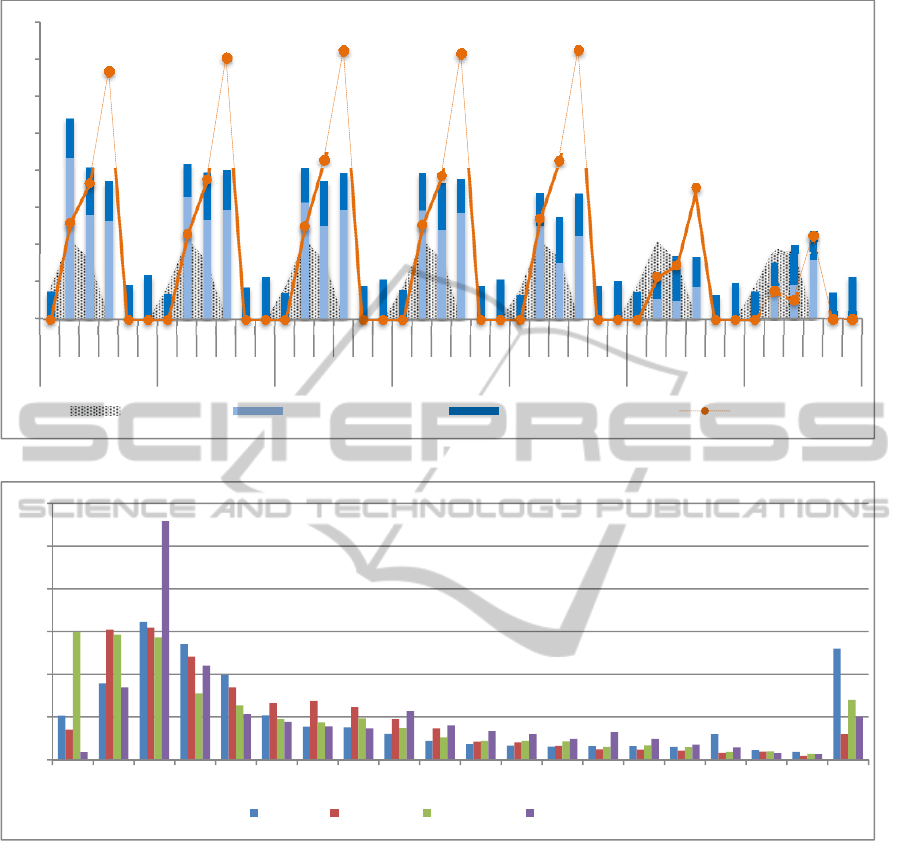
Figure 2: Distribution of inpatient ward input-output flows.

Figure 3: LOS distributions (in days) in the inpatient wards- elective patients.

while emergent ones are more equally distributed.

This phenomenon is quite reasonable and must be

taken into account to effectively plan the bed

allocation. Discharges are distributed in three slots

(i.e. 7_10, 10_13, 13_16). The most of discharges

are placed in the last slot of the day (13-16), just

after the launch and after the ward rounds.

Figure 3 and Figure 4 show the distribution of

the length of stay (LOS) for each ward, for elective

and emergent patients, respectively. On the x-axis,

the length of stays in days are represented, while on

y-axis the % of patients is reported for each ward

where they have been admitted.

The largest number of emergent patients exits

the ED with a decision to be admitted into one of the

medicine wards and their stay is quite short (the

largest number remain for no more than 3 days). The

elective patients are more equally distributed over

different wards, in fact the most stay in the “other”

group which contains all the wards but medicine,

orthopaedics and surgery. The average length of stay

is greater in this case. More elective patients are

admitted into surgery wards with respect to the

emergent ones and the length of stay is on average

greater.

The data analysis highlights some phenomena

which can be addressed by the model to simulate

different bed manager rules (i.e. decision about the

ward where an emergency patient should be

admitted) and hospital organizations (i.e. slots and

frequencies of patients discharge and elective

admissions).

0_7

7_10

10_13

13_16

16_19

19_24

0_7

7_10

10_13

13_16

16_19

19_24

0_7

7_10

10_13

13_16

16_19

19_24

0_7

7_10

10_13

13_16

16_19

19_24

0_7

7_10

10_13

13_16

16_19

19_24

0_7

7_10

10_13

13_16

16_19

19_24

0_7

7_10

10_13

13_16

16_19

19_24

Monday Tuesday Wednesday Thursday Friday Saturday Sunday

Transferred Elective admissions Emergent admissions Discharged

10%

15%

20%

25%

30%

1234567891011121314151617181920

Other Surgery Medicine Orthopaedics

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

906

Figure 4: LOS distributions (in days) in the inpatient wards - emergent patients.

4 MODEL VALIDATION AND

STEADY STATE CONDITIONS

The DES model has been implemented using the

simulation software environment Witness (Witness,

2013) and has been be validated to ensure that the

simulation outputs adequately represented the real

data of the system under investigation by adopting

appropriate statistical tests (Law, 2007). There are

numerous techniques for validating a simulation

model; some of them are based on subjective

graphical analysis, some others on mathematical

statistics to obtain quantitative data about the quality

of the simulation model.

Firstly, the model validation has been performed

to verify if and to which extent the model is able to

represent the real flows of elective and emergent

patients within the system under investigation.

Referring to the logic and rules implemented to

simulate the bed manager decisions a face validation

(Law, 2007) has been firstly performed with the

hospital managers and clinicians which gave us

many insights to adapt the model to the current

practice and render it a truer representation of the

real system. Besides, the simulation outputs have

been compared to the real data using a classical

parametric statistical test, i.e. the T-test (Law, 2007).

In particular, we compared two output measures,

i.e. number of emergent patients to be admitted and

number of total patient admissions (for each

inpatient ward). Note that the last metric includes the

emergent and elective admissions as well as the

transferrals among different inpatient wards. The

simulated output measures were obtained through 20

IID replications and then compared against the same

real measures for the reference time period, i.e. one

year. We decided to test the null hypothesis H

under a probability of rejecting the model fixed to

the



=0.05 level. The corresponding critical value of

the test is t

n-1,1-/2

= t

19, 0.975

= 2.093; from Table 4 we

can see that t

(19)

 2.093 for all values and hence our

simulation model has been proved to represent the

real behaviour with a low probability of error.

Table 4: Comparison between real data and simulated

output.

# of emergent admissions

W1 W2 W3 W4

Real measures

12349 948 1173 5299

Simul. outputs

12382 954 1162 5321



0.27% 0.63% 0.94% 0.42%

T-test (t

)

1.932 2.065 2.088 1.989

Since the aim of our simulation study is to derive

a set of performance indices able to evaluate the

efficiency of the system under study, it is important

to choose the conditions under which a steady state

behaviour in the simulation is reached (Law, 2007).

To obtain the steady state conditions we have

used the batch means method, based on a single run

of data collection, which has been divided into 10

batches. The decision of using 10 sampling batches

is due to the results of the initial experimentation

10%

15%

20%

25%

30%

35%

40%

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 >20

Other Surgery Medicine Othopaedics

ADiscreteEventSimulationModeltoSupportBedManagement

907

with the simulation model, that revealed a relatively

small variance in the system output.

The first run begun at time t

= 0 corresponding to

the empty initial state of the system; therefore, a

preliminary simulation time was needed to clean out

the transient simulation period. After this initial

warm-up fixed to 90 days, we reset the statistics of

the model and run it starting by the new initial time

=2160 (hours) until the ending time condition

=88560, so that each batch represents 360 days of

steady-state simulation. The results presented in the

next section are the average of the performance

indices sampled for the 10 batches.

5 SCENARIOS ANALYSIS AND

PRELIMINARY RESULTS

Once validated, the discrete event simulation model

has been used to analyze the effects on system

behavior of different bed management rules and

inpatient ward organization and verify their

effectiveness to face the bed allocation problem.

For the output analysis we used the set of

performance metrics reported in Section 2.1 which

allow to assess the performance of the system from

both the patient point of view (waiting time before

admission and elective admission postponements)

and the hospital point of view (bed utilization rate

and misallocation indexes).

Three set of scenarios and related results are

herein presented (Table 5).

In the first set of scenarios (Scenarios 0-3) the

system rules of the bed management are modified

with respect to the number and timing of the

evaluation of available beds and ability to look

ahead. In particular, in the baseline scenario

(Scenario 0) the bed manager simply verifies, for

each emergent patient to be admitted in the inpatient

wards, if there is a free bed available in the ward

assigned to her/him, if not it checks the bed

availability in the other wards and when it finds a

free bed sends the patient to the first ward with a

free bed available even if misallocated. Including the

“timing” characteristic (Scenario 1) gives the bed

manager the ability to postpone at most 4 times the

assignment of a patient to a “wrong” ward in order

to verify if after a short time (usually half an hour)

some beds will be available. The number of times

the BM can postpone its decision as well as the

period between the re-evaluations are also key

parameters. In the preliminary tests herein presented

they are set at 4 re-evaluation, every 30 minutes, i.e.

at least the bed manager can postpone its decision to

admit for 2 hours. The ability to long-ahead

(Scenario 2 and 3) allows the BM to consider in

each time slot not only the number of beds available

but also the expected number of elective patients to

be admitted during the day.

Table 5: Scenarios analysis.

Scenario

Bed

manager

timing

Bed

manager

look

ahead

Elective

admiss.

blocking

New

discharge

policy

Scenario0

Scenario1

Scenario2

Scenario3

x x

Scenario4

x x x

Scenario5

x x x

In the second series of results (Scenario 4 and 5)

the idea is to block (not schedule) or reduce the

elective admission during the days and slots where

peaks in the ED admissions are expected, for

instance on Monday, slot 7-10, (see Figure 2 and

Figure 5). These is scenario tries to manage the

inpatient demand flow in order to smoothing the

flow of emergent patients coming from the ED.

Finally, the third analysis is intended to manage

the supply flow, i.e. to change the discharge policy

to shortening as much as possible the length of stay

(Scenario 6 and 7). The usual proposal is to transfer

patients likely to be discharged during the day and

(waiting only for the next visit by the consultant), in

a dedicated room (referred as discharge room or

lounge). This allows freeing in advance some beds

since the morning, instead of the first afternoon as it

usually happens in the current practice observed.

This analysis can also be designed to verify the

impact of removing some administrative barriers or

modifying the work shifts and roastering of the

inpatient ward staff, thus allowing discharges on

Saturday and Sunday, or late evening, thus

smoothing the in and out flows during the day and

avoid useless stays.

The results are reported in Table 6. For each

scenario the resulting values of the performance

indexes reported in Section 2.1 are given.

Introducing the re-evaluation in the BM

behaviour reduces the number of misallocated

patients. Moving from scenario 0 to scenario 1 and

from scenario 2 to 3, the total number of patients

misallocated is reduced of about 61% and 83%,

respectively, thus resulting in a reduction of the

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

908

Table 6: Scenarios analysis results.

Indexes

Scenario

# of patients misallocated (W1) 376 175 1133 227 163 138

# of patients misallocated (W2) 0 0 38 0 0 1

# of patients misallocated (W3) 5 0 29 0 1 3

# of patients misallocated (W4) 238 64 1070 141 25 87

Total # of patients misallocated 619 239 2270 368 189 229

Misallocation index (W1) 2,959 1,3973 9,0351 1,814 1,2944 1,0980

Misallocation index (W2) 0,000 0,0000 3,7924 0,000 0,0000 0,1067

Misallocation index (W3) 0,419 0,0000 2,3829 0,000 0,0853 0,2555

Misallocation index (W4) 4,163 1,1140 18,8646 2,497 0,4365 1,5029

Avg. Misallocation index 3,005 1,1706 11,1106 1,805 0,9252 1,1188

Avg. # of ED patients to be admit. in W1 2,933 2,667 2,200 1,133 2,000 1,584

Avg. # of ED patients to be admit. in W2 0,200 0,067 0,467 0,000 0,600 0,234

Avg. # of ED patients to be admit. in W3 0,067 0,400 0,467 0,800 0,000 0,200

Avg. # of ED patients to be admit. in W4 0,933 1,533 1,000 2,667 1,600 1,800

Avg. # of ED patients to be admitted 1,033 1,167 1,033 1,150 1,050 0,955

Waiting time before admission (W1) 1,799 2,560 2,584 2,986 2,828 2,528

Waiting time before admission (W2) 1,576 1,603 1,673 1,667 1,700 1,600

Waiting time before admission (W3) 1,564 1,751 1,736 1,677 1,681 1,681

Waiting time before admission (W4) 1,705 2,228 2,063 2,543 2,286 2,342

Avg. waiting time before admission 1,661 2,035 2,014 2,218 2,124 2,038

# postponed elective admissions (W1) 73 126 8 93 54 66

# postponed elective admissions (W2) 0 0 23 0 0 0

# postponed elective admissions (W3) 4 0 11 0 0 0

# postponed elective admissions (W4) 627 616 41 211 72 101

Total # postponed elective admissions 704 742 83 304 126 167

Bed utilization rate (W1) 92,350 92,520 92,420 92,320 91,680 92,380

Bed utilization rate (W2) 67,210 66,310 79,660 68,060 66,730 67,730

Bed utilization rate (W3) 73,490 70,020 75,930 71,250 70,010 72,230

Bed utilization rate (W4) 92,690 92,490 90,710 92,750 89,280 91,450

Avg. bed utilization rate 81,435 80,335 84,680 81,095 79,425 80,948

misallocation indexes as well. This is correlated with

an increase of the number of patients waiting to be

admitted and their average waiting time. Beside the

waiting time to be admitted never grows of more

than one hour. The introduction of the look-ahead

characteristics (Scenario 2 and 3) has a major impact

on reducing the number of postponed elective

admissions. By including both the decision

postponements and the look-ahead in the BM rules

(Scenario 3) the number of patients misallocated and

the number of elective patients postponements is

reduced of about 40%.

Looking at the detailed slot time results a major

problem is shown in some shifts where the number

of patients to be admitted grows since no bed are

available in the inpatient wards, for example on the

afternoon slots of Monday (Figure 5). Moving o this

direction, Scenario 4 and Scenario 5 are directed to

manage the flow of elective admissions and

discharges, respectively, in order of smoothing the

flow of emergent patients coming from the ED and

better synchronize them with the inpatient ward

flows.

The first strategy (i.e. reducing the elective

admissions of the slots where peaks in the emergent

admissions are observed) shows to be more effective

in reducing the number of misallocations and the

number f elective patients postponements, while the

ADiscreteEventSimulationModeltoSupportBedManagement

909

Figure 5: Number of ED waiting patients to be admitted on Monday for each time slot.

second performs better in reducing the number of

patients waiting in ED to be admitted and their

waiting time.

Finally, it must be noticed a problem related to

the bed capacity of ward group 1 and 4. The

utilization rate of those ward group are more than

90% and all the scenarios tested little impact on

these performance metrics.

Future direction of the research will be also

devoted to verify the impact of an alternative

assignment of the beds among the ward groups on

the system performance.

Note that the three kinds of analysis entail

different tactical and organizational decisions to be

taken from the hospital management.

There are, of course, many other possibilities, not

herein taken into consideration, which imply

strategic decisions. For example, facilitating the

discharge of elderly patients by improving the

continuity of care and linking the discharge

coordinator with the social services; extending the

hours of community nurse team by increasing the

home assistance and the transferrals to the

intermediate care ward, i.e. lower intensity ward,

(Boaden et al, 1999).

It should be pointed out that the second and third

groups of scenarios entail additional costs, even not

necessarily financial costs. Blocking the elective

admissions in some days, for instance, generates a

lengthening of waiting lists for elective patients

(social cost) or cancelations (financial cost); the

supply side scenarios assume to set up a dedicated

room (organizational cost) and/or requires higher

staff costs to manage the discharges in different and

enlarged time periods.

Besides determining the impact and benefits of

alternative scenarios by means of the chosen set of

performance metrics, costs should also be estimated

and taken into account.

6 CONCLUSIONS AND FUTURE

WORKS

In this paper we developed a decision support

framework for analysing the patient flows between

an hospital Emergency Department and the inpatient

stay wards of the same hospital.

The framework has been applied to a real case

study of the teaching hospital San Martino sited in

the city of Genova Surgery (Italy).

The main conclusion is that, in principle, a

decision tool cannot individuate the best solution,

but rather can help in assessing the direct and

indirect impact of different BM working rules as

well as of alternative organizations of the stay wards

aimed at facilitating the integration and

synchronization of the flows between ED and

inpatient wards.

The model underlying the bed manager decisions

affects how other hospital resources, such as

operating theatres and elective inpatients wards

perform since all hospital services are dependent on

bed availability. In turn, other hospital department

inefficient performance, mainly lengthening hospital

stays, can impact, upon ED crowding. This study has

recognised this effect in line with the literature

findings.

The so-called "bed management" is a business

function that allows increasing the efficient use of

beds, in order to optimize the flow of patients within

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

910

the hospital. It is a crucial function within an

organization based on process activities. Improving

patient flow is a way of improving health services.

The model herein developed could be used as a

decision support tool for a priori verifying the

effects of different bed management rules both by a

patient and hospital point of view.

Of course the model could include other patient

characteristics and patient flows also versus other

hospital facilities and can easily be adapted to

simulate other case studies, changing the system

constraints and the organizational models of the ED

and hospital wards.

Future work will be directed to perform an

extensive scenario analysis and compare the results

with a larger amount of real data and performance

indexes.

Moreover, future research are going to explore

the potentiality of applying the optimization module

integrated in the simulation software environment, in

order to determine the optimal decision pertaining

the number of beds to be assigned to each ward

group, able to optimize ad hoc chosen objective

functions, such as maximizing the bed utilization

rate, minimizing the number of postponed patients

or the overall misallocation index.

ACKNOWLEDGEMENTS

The authors acknowledge support from the Italian

Ministry of Education, University and Research

(MIUR), under the grand FIRB n. RBFR081KSB.

Data have been made available thanks to a

collaboration between ARS Liguria (Dr. Francesco

Quaglia and Domenico Gallo) and the Department

of Economics and Business, University of Genova.

REFERENCES

Agenas (National Agency for Health Care Services), 2012.

Monitor, Special Issue on the Emergency System.

Roma, http://www.agenas.it/pubblicazioni/monitor-

rivista-agenas.

Audit Commission, 1992. Lying in Wait: the Use of

Medical Beds, in Acute Hospitals. HMSO. London.

Audit Commission, 1993. Bed Management. HMSO.

London.

Bagust, A., Place, M., Posnett, J., 2003. Dynamics of bed

use in accommodating emergency admissions:

stochastic simulation model. British Medical Journal,

310 (7203), 155-158.

Boaden, R., Proudlove, N., Wilson, M., 1999. An

exploratory study of bed management. Journal of

Management in Medicine, 13 (4), 234-250.

Evans, B., Potvin, C., Johnson, G., Henderson, N., Yuen,

I., Smith, T., Metham, S., Taylor, S., Sniekers, D.,

2011. Enhancing Patient Flow in Acute Care Hospital:

Successful Strategies at the Juravinski Hospital.

Healthcare Quarterly, 14 (3), 66-75.

Green, J,. Armstrong, D,. 1994. The views of service

providers. In Morrell, D., Green, J., Armstrong, D.,

Bartholomew, J., Gelder, F., Jenkins, C., Jankowski,

R., Mandalia, S., Britten, N., Shaw, A., Savill, R. (eds)

Five Essays on Emergency Pathways, Institute, for the

Kings Fund Commission on the future of Acute

Services in London, Kings Fund, London.

Haraden, C., Resar, R., Horton, S.S., Henderson, D.,

Dempsey, C., Appleby, D., 2004. Capacity

Management: Breakthrough Strategies for Improving

Patient Flow. Frontiers of Health Services

Management, 20 (4), 3-15.

Harper, P.R., Shahani, A.K., 2002. Modelling for the

planning and management of bed capacities in

hospitals. Journal of the Operational Research

Society, 53, 11–18.

Health Foundation, 2013. Improving patient flow across

organisations and pathways. (retrived from

http://www.health.org.uk/public/cms/75/76/313/4196/I

mproving%20patient%20flow.pdf?realName=TxPs1T.

pdf).

Howell, E., Bessman, E., Kravet, S., Kolodne,r K.,

Marshall, R., Wright, S., 2008. Active Bed

Management by Hospitalists and Emergent

Department Throughput. Annals of Internal Medicine,

149; 804-810.

Howell, E., Bessman, E., Marshall, R. Wright, S., 2010.

Hospitalist bed management effecting throughput from

the emergency department to the intensive care unit,

Journal of Critical Care, 7(2); 184-189.

IHI, Institute for Healthcare Improvement, 2003.

Optimizing Patient Flow. Moving Patients Smoothly

Through Acute Care Settings. Innovation Series 2003

paper, online article, retrieved June 14th 2014,

http://hospitalmedicine.ucsf.edu/improve/optimizing_

pt_flow_white_paper2003.pdf .

Jensen, A1, Boyle, J, Khanna, S., 2013. Visualising patient

flow. Health Technology Information, 178, 77-82.

Istat (National Institute Statistics in Italy), 2011. http://noi-

italia2011.istat.it/index.php?id=7&user_100ind_pi1%

5Bid_pagina%5D=88&cHash=b52e8996296b53cd14c

5ef201bda574a.

Law M.A., 2007. Simulation Modeling & Analysis.

McGraw-Hill, 4th ed.

Simeu, 2011. Standard organizzativi delle strutture di

emergenza e urgenza. Organizational standards of

A&E facilities, http://www.comesemergenza.it/files/

Standard_FIMEUC-SIMEU_2011.pdf (retrieved June

24th, 2014).

Proudlove, N., Gordon, K., Boaden, R., 2003. Can good

bed management solve the overcrowding in A&E?.

Emergency Medicine Journal, 20 (2), 149-155.

ADiscreteEventSimulationModeltoSupportBedManagement

911

Proudlove, N., Boaden, R., Jorgensen, J., 2007.

Developing bed managers: the why and the how.

Journal of Nursing Management, 15, 34-42.

Tortorella, F., Ukanowicz, D., Douglas-Ntagha, P., Ray,

R., Triller, M., 2013. Improving bed turnover time

with a bed management system. J Nurs Adm;43 (1),

37-43.

Young, T., Brailsford, S., Connell, C., Davies, R., Harper,

P., Klein, J.K., 2004. Using industrial processes to

improve patient care. British Medical Journal, 328,

162–4.

Vissers, J., Beech, R., 2005. Health Operations

Management: Patient Flow Logistics in Health Care.

Routledge, Oxon.

Vanberkel, P.T., Boucherie, R.J., Hans, E.W., Hurink,

J.L., Litvak, N., 2009. A Survey of Health Care

Models that Encompass Multiple Departments,

http://eprints.eemcs.utwente.nl/15762/01/memo1903.p

df.

Witness (2013). User guide. Lanner Group, London, U.K.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

912