RNN-based Model for Self-adaptive Systems

The Emergence of Epilepsy in the Human Brain

Emanuela Merelli and Marco Piangerelli

School of Science and Technology, Computer Science Division, University of Camerino, Camerino, Italy

Keywords:

LSTM-RNNs, Brain functional activities, epilepsy, complex systems, S[B] Paradigm.

Abstract:

The human brain is the self-adaptive system par excellence. We claim that a hierarchical model for self-

adaptive system can be built on two levels, the upper structural level S and the lower behavioral level B.

The higher order structure naturally emerges from interactions of the system with its environment and it acts

as coordinator of local interactions among simple reactive elements. The lower level regards the topology

of the network whose elements self-organize to perform the behavior of the system. The adaptivity feature

follows the self-organizing principle that supports the entanglement of lower level elements and the higher

order structure. The challenging idea in this position paper is to represent the two-level model as a second

order Long Short-Term Memory Recurrent Neural Network, a bio-inspired class of artiﬁcial neural networks,

very powerful for dealing with the dynamics of complex systems and for studying the emergence of brain

activities. It is our aim to experiment the model over real Electrocorticographical data (EcoG) for detecting

the emergence of long-term neurological disorders such as epileptic seizures.

1 INTRODUCTION

A self-adaptive system is “a closed-loop system with

a feedback loop aiming to adjust itself to changes dur-

ing its operation” (Salehie and Tahvildari, 2009) and

also “a system capable to adjust its behavior in re-

sponse to its perception of the environment and of

the system itself” (Cheng et al., 2009). Furthernore a

complex system is, roughly speaking, a system made

by a huge, ﬁnite, number of components interacting

each other in a nonlinear way, with some peculiar

abilities to self-organize and to exhibit an emerging

behavior

. According to these two deﬁnitions, most

of biological systems are complex systems, whose

behavior is self-adaptive because it evolves to adapt

to new environmental conditions. Two important ex-

amples are the human brain, described as complex

networks (Sporns et al., 2004), and the human im-

mune system, as a metaphor of a self-adaptive system

(Merelli et al., 2014). The human brain is made up

by about 10

(one hundred billion) excitable cells:

the neurons. They are linked each other in a com-

plex network by about 10

(one million of billion)

synapses, that in turn can produce an enormous num-

ber, about 10

, of different patterns of connectivity:

http://www.dym-cs.eu/

the possible emerging behaviors of the brain. More-

over, the brain can be seen working at two levels, the

higher one coordinates the interactions among neu-

rons and the lower one performs the functional activ-

ities by regulating the strengths of their synapses or

physically rewires their connections (see Figure 4 in

Section 3). This feature, known as plasticity, allows

the brain to properly adapt to new environmental con-

ditions (Ashby and Isaac, 2011). Thus, studying the

human brain requires a dramatic change in paradigms

that sees reductionism challenged by holism where

brain activities and its pathologies, such as epilepsy,

can be discovered as “emerging behaviors” of the

system-brain. Nowadays formal modeling of self-

adaptive systems has been advocated as a way to deal

with complex systems (Merelli et al., 2012; Khakpour

et al., 2012; Bruni et al., 2012). Therefore, we con-

sider complex systems as systems that “live” in an en-

vironment with which interact, by perceiving and re-

acting to environmental events, and by learning and

adapting to new conditions by exposing new beha-

viors. Moreover, they are in a sort of dynamic equilib-

rium: the systems remain in the state of equilibrium

until external conditions do not change. When new

conditions arise, it must adapt by evolving to reach a

new state of equilibrium. Consequently, the human

brain might be modelled as a self-adaptive system.

356

Merelli E. and Piangerelli M..

RNN-based Model for Self-adaptive Systems - The Emergence of Epilepsy in the Human Brain.

DOI: 10.5220/0005165003560361

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 356-361

ISBN: 978-989-758-054-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

We claim that a self-adaptive system can be mo-

deled with a hierarchical model built on two basic le-

vels: an upper structural level S, describing the adap-

tation dynamics of the system, and a lower behavioral

level B, accounting for the behaviour of the system.

The upper level acts as coordinator of local interac-

tions among elements, that ﬁll up the lower behavioral

level. As a consequence, the higher order structure

emerges from the interaction of the system with its en-

vironment, and the adaptivity feature follows the self-

organizing principle that supports the entanglement of

lower level elements and the higher order structure.

In this proposal, we aim to exploit our recent expe-

rience in collecting real-time electrocorticographical

data (EcoG) of epilepsy (Piangerelli et al., 2014), a

neurological disorder traditionally viewed as a “hy-

persynchronous” activity (Kramer et al., 2010) of the

neurons in the brain, for modeling this process as an

emerging pathology of the brain activity. We want

to study a reason why the adaptation phase failed, to

this end we start to pose some key-questions: “how

the brain process can be modeled as a self-adaptive

system? How can a model freely evolve to allow the

system to adapt?’ What does it mean that the system

cannot adapt or it adapts in a wrong way?”.

By taking into account our previous work, inspired by

the immune system (Merelli et al., 2014), where the

adaptation phase is represented as a topological appli-

cation of the S[B] paradigm suitable to identify, clas-

sify and learn new relationships among antibodies, in

this position paper we address the above questions by

building a hierarchical model as a Recurrent Neural

Networks (RNN) application of the S[B] paradigm.

RNNs are a bio-inspired class of artiﬁcial neural net-

works very powerful for dealing with the dynamics of

complex systems and for studying the emergence of

brain activities, to develop a self-adaptive model able

to discriminate between the physiological and patho-

logical human brain processes; in particular, between

the physiological and epileptic conditions. The chal-

lenging idea is to describe the S[B] two-level model

as a second order Long Short-Term Memory (LSTM)

Recurrent Neural Network. The LSTM-RNN ar-

chitecture was introduced in 1997 (Hochreiter and

Schmidhuber, 1997). Like most RNNs, a LSTM net-

work is universal in the sense that, given the proper

weight matrix, it can compute anything a conven-

tional computer can compute as program.

2 RECURRENT NEURAL

NETWORKS: A POWERFUL

METHOD

Artiﬁcial Neural Networks (ANN) are computational

(non-linear) models biologically inspired by human

central nervous system (brain). They consist in a set

of nodes, also called neurons or processes, connected

each other like the real neurons, and able to process

input signals. The ability of learning is exactly the

most important feature of an ANN: learning means

evolving and adapting to the changing context for re-

acting to different situations. A kind of self-adaptive

system with an hidden adaptivity phase. The simplest

example of an ANN is the McCulloch-Pitts neuron

(McCulloch and Pitts, 1943), followed by perceptron,

whose limit was overcome by the introduction of mul-

tilayered perceptrons with back-propagation, known

as FeedForward Neural Networks (FFNN). Details

about this subject can be funded in (Minsky and Pa-

pert, 1988).

Nowadays a great interest is rising upon artiﬁcial

Recurrent Neural Networks that differ with respect to

FFNNs in modeling the neurons with the ability to

sending feedback signals to each others neurons (see

Figure 1).

Figure 1: An example of RNN. This network presents feed-

back connection but it is fully connected too. Not all the

RNNs are required to be this way.

2.1 The RNN Strong Points and

Limitations

The main features of RNNs, due to the presence of

loops, are basically three:

• RNNs develop a system dynamics even without

input signals;

• RNNs are able to store, in their hidden layers, a

non-linear transformation of the input. They have

memory of past inputs;

RNN-basedModelforSelf-adaptiveSystems-TheEmergenceofEpilepsyintheHumanBrain

357

• the rate of change of internal states con be ﬁnely

modulated by the recurrent weights to give robust-

ness in detecting distortions of input data.

RNNs are universal approximations of any dynamical

system (Funahashi and Nakamura, 1993); the brain it-

self can be seen having an RNNs-architecture (Ashby

and Isaac, 2011) (see Figure 2). Cortical networks

present an incredible ability to learn and adapt via a

number of plasticity mechanisms which affect both

their synaptic and neuronal properties. The self-

adaptive mechanism might allow the recurrent net-

works in the cortex to learn representations of com-

plex spatio-temporal stimuli. Neuronal responses are

highly dynamic in time (even with static stimuli)

and contain a rich amount of information about past

events, i.e. memory. This can be the reason why they

Figure 2: (Left) The brain as a functional recurrent network

(van den Heuvel and Sporns, 2011). (Right) A drowning of

a recurrent anatomical network in the brain.

are biologically more plausible and computationally

more powerful than other adaptive approaches such as

Hidden Markov Models, they have no memory at all,

FFNNs and Support Vector Machines (SVM). One of

the main problem is the relative low storage capacity

meaning that the inﬂuence of a given input either de-

cays or exponentially blows up since it cycles around

the net’s loops. This problem is well know as vanish-

ing gradient problem, it does not allow past events to

inﬂuence present events.

2.2 Long Short-term Memory

Recurrent Neural Networks

Long Short-Term Memory Recurrent Neural Net-

works are a particular architecture of RNNs. The ba-

sic unit of an LSTM network is the memory block,

such as the one shown in Figure 3, containing one

or more memory cells and three adaptive, multiplica-

tive gating units shared by all cells in the block.

Each memory cell has at its core a recurrent self-

connected linear unit (orange) called the “Constant

Error Carousel” (CEC). The CEC rules constant error

ﬂow, and overcomes a fundamental problem plagu-

ing previous RNNs preventing error signals from de-

caying quickly as they “get propagated back in time”.

The adaptive gates (green) control inputs and outputs

of the cells (input and output gate) and learn how to

reset the state of the cell once its contents are obso-

lete (forget gate). All errors are cut off once they

leak out of a memory cell or gate. Although they

are useful to change the incoming weights. The re-

sult is that the CECs are the only part of the system

through which errors can ﬂow back forever, whereas

the gates learn the nonlinear aspects of sequence pro-

cessing. LSTM learning algorithm is local in space

and time and O(1) is its computational complexity per

time step and weight. Sufﬁce it to say here that the

simple linear unit is the reason why LSTM nets can

learn to discover the importance of events that hap-

pened 1000 discrete time steps ago, while previous

RNNs already fail in case of time lags exceeding as

few as 10 steps.

LSTM networks overcome the vanishing gradient

problem connected with RNNs allowing to store and

access information over a long period of time time.

This makes an LSTM network well-suited to learn

from experience, to classify, process and predict time

series when there are very long time lags of unknown

size between important events. Recent applications of

RNNs are handwriting recognition, speech recogni-

tion, image classiﬁcation, stock market (time series)

prediction and motor control and rhythm detection.

LSTM RNN are second-order neural networks (NNs):

the gate units serve as the additional sending units for

the second-order connections (Monner and Reggia,

2012). By second-order NNs, we mean a network that

not only it allows normal weighted connections from

one sending unit to one receiving unit, but also it al-

lows second-order connections: weighted links from

two sending units to one receiving unit. In this case

the signal received is dependent upon the product of

the activities of the sending units with each other and

the connection weight (Miller and Giles, 1993).

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

358

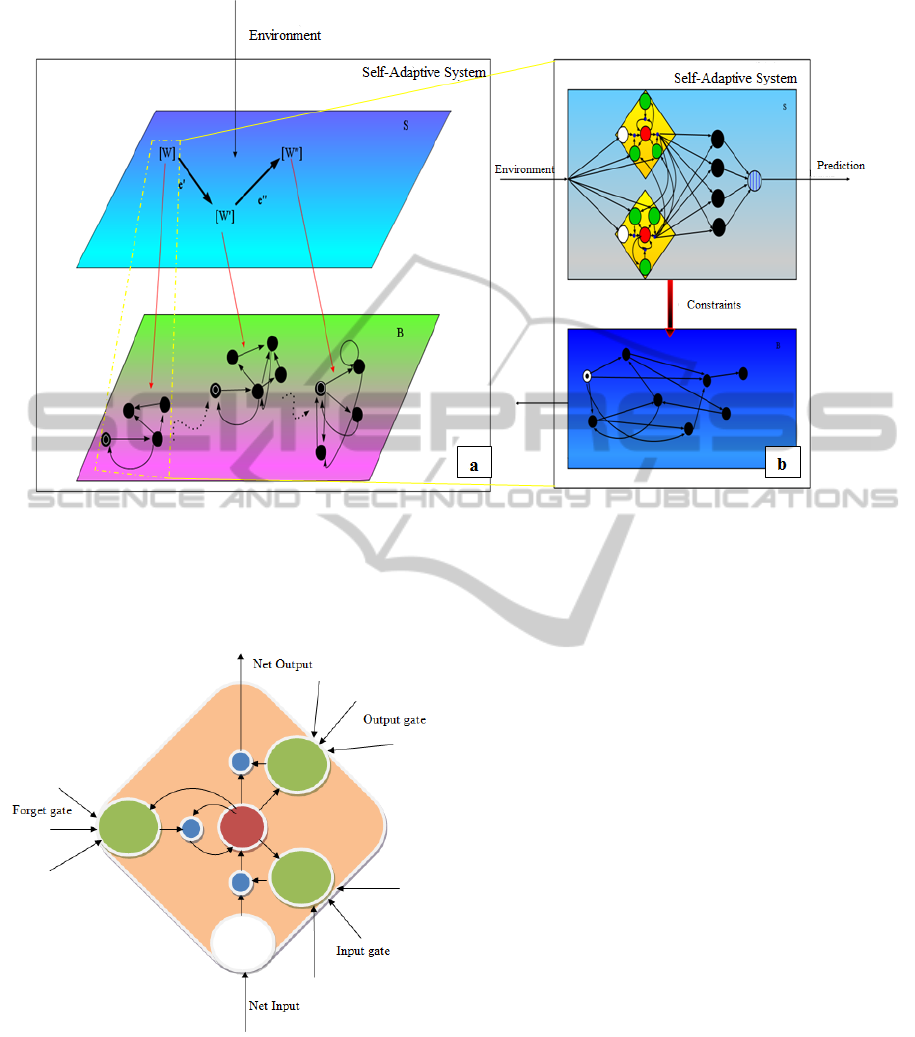
Figure 4: A schematic view of a self-adaptive system. On the left, the panel (a) shows the evolution of the system: LSTM

RNNs are indicated by their weight matrix [W] and some events e could make the system adapt and evolve changing the

weight matrix. For each weight matrix is possible to obtain a DFA describing the behavior of the system. On the right, the

panel (b) describes in a more detailed way an instant of the evolution: it is possible to see a LSTM-RNN and the related DFA.

Figure 3: A LSTM cell. The linear unit lives in a cloud of

nonlinear adaptive units needed for learning nonlinear be-

havior. Here we see an input unit (white) and three (green)

gate units; small blue dots are products. The gates learn to

protect the linear unit from irrelevant input events and error

signals.

3 EMBEDDING RNNS IN A

HIERARCHICAL MODEL FOR

SELF-ADAPTIVE SYSTEM:

THE IDEA

As explained in the previous section, RNNs have been

shown to be a powerful tool to deal with different is-

sues regarding adaptivity. That is the reason why we

believe that they might be used with proﬁciency in

the development of a model for self-adaptive systems

based on the architecture shown in Figure 4. The

model should consist in two levels: the reactive Be-

havioral B level and the intelligent Structural S level.

S is the “brain” of our model, it is able to sense all

the external stimuli and represent them as a set con-

straints (the weigh matrices [W ] in the Figure 4) those

that will guide the B level to react with a correct be-

havior. Whenever the B level can not anymore satisfy

the set of constraints imposed by S, must evolve its

network topology to adapt its behavior to the new set

of constraints, by using the real RNN weight matrix.

The general framework presented in Figure 3 of the

paper (Merelli et al., 2014) remains valid if we con-

sider as invariants of the model a measure of the net-

work topology for example the RNN weight matrix.

RNN-basedModelforSelf-adaptiveSystems-TheEmergenceofEpilepsyintheHumanBrain

359

The evolution of the model relies on how the coding

of the set of perceptions (data space in the ﬁgure) that

the brain will be store within the S level and on how

the corresponding B level will be modeled. Thus the

general approach based on the use of RNNs can be

view as an application of the S[B] paradigm.

To facilitate the concrete application of the S[B]

paradigm we are going to use, as a collection of data,

the set of electrical signals of the brain (time series),

that are the proofs of the brain activity. They con-

tain all the information regarding the (topological net-

work, such as the) internal states of the brain and

its connectivity. They are the input data for train-

ing a LSTM RNN whose topology will be measured

to characterized the adaptation phase of the proposed

model. According to the work of Giles and others

(Giles et al., 1992) a second-order recurrent neural

network can be mapped into a Final State Automa-

ton (DFA), likewise the LSTM RNNs will be likely

mapped into the classes of DFAs whose correspond-

ing set of accepted regular terms will be used to

describe the cerebral activities and discriminate the

physiological from the pathological one.

The real data over which we will experiment

the proposed approach are the electrocorticographi-

cal signals: they are recorded using a new device,

the ECOGIW-16E (Piangerelli et al., 2014; Cristiani

et al., 2012), developed by two Italian companies:

AB-MEDICA s.p.a. and Aethra Telecommunications

s.r.l.. the device, completely wireless will provide a

huge amount of data, continuously recording electri-

cal brain activity.

4 FINAL REMARKS

Starting from the description of the human brain as

a self-adaptive system and exploiting the features of

the second-order LSTM-RNNs, we proposed to de-

velop a hierarchical model made up by two levels, S

the structural one and B the behavioral one, entangled

via a unique adaptation phase. The study of the evo-

lution of the model, rested on the adaptation phase, is

characterized by the way in which the space of data

is analyzed. In our scenario, the space of data repre-

sents the environment, the set of perceptions through

which the behavior of a system evolves and its knowl-

edge updates. We proposed to analyze the set of data

by an RNN for deriving the so called weight matrix

that allows us to build the corresponding complex net-

work that represents the emerging model at the cur-

rent time. In the study of the evolution of the com-

plex network, we aim to consider the recent impor-

tant results reached by some researchers of the TOP-

DRIM project

(Franzosi et al., 2014): a geometric

entropy measuring networks complexity for detect-

ing the emergence of the “giant component” as the

emergence of a neurological disorders such as epilep-

tic seizures.

ACKNOWLEDGEMENTS

We would like to thank to Regione Marche and Aethra

Telecommunications s.r.l. for partially funding Pian-

gerelli’s Ph.D. studies with the Eureka Project.

We also acknowledge the ﬁnancial support of the

Future and Emerging Technologies (FET) programme

within the Seventh Framework Programme (FP7) for

Research of the European Commission, under the

FET-Proactive grant agreement TOPDRIM, number

FP7-ICT-318121.

REFERENCES

Ashby, M. C. and Isaac, J. T. R. (2011). Maturation of a

recurrent excitatory neocortical circuit by experience-

dependent unsilencing of newly formed dendritic

spines. Neuron, 70(3):510–21.

Bruni, R., Corradini, A., Gadducci, F., Lluch Lafuente, A.,

and Vandin, A. (2012). A conceptual framework for

adaptation. In Fundamental Approaches to Software

Engineering, volume 7212 of Lecture Notes in Com-

puter Science, pages 240–254. Springer.

Cheng, B., Lemos, R. D., and Giese, H. (2009). Soft-

ware engineering for self-adaptive systems: A re-

search roadmap. Software engineering for . . . , pages

1–26.

Cristiani, P., Marchetti, S., Paris, A., Romanelli, P., and

Sebastiano, F. (2012). Implantable device for ac-

quisition and monitoring of brain bioelectric signals

and for intracranial stimulation. WO Patent App.

PCT/IB2012/051,909.

Franzosi, R., Felice, D., Mancini, S., and Pettini, M. (2014).

A geometric entropy measuring network comcomplex

(submitted).

Funahashi, K. and Nakamura, Y. (1993). Approximation of

dynamical systems by continuous time recurrent neu-

ral networks. Neural Networks, 6(6):801–806.

Giles, C. L., Miller, C. B., Chen, D., Chen, H.-H., Sun,

G.-Z., and Lee, Y.-C. (1992). Learning and extract-

ing ﬁnite state automata with second-order recurrent

neural networks. Neural Computation, 4(3):393–405.

Hochreiter, S. and Schmidhuber, J. (1997). LONG SHORT

- TERM MEMORY. 9(8):1–32.

Khakpour, N., Jalili, S., Talcott, C., Sirjani, M., and

Mousavi, M. (2012). Formal modeling of evolv-

ing self-adaptive systems. Sci. Comput. Program.,

78(1):3–26.

www.topdrim.eu

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

360

Kramer, M. A., Eden, U. T., Kolaczyk, E. D., Zepeda,

R., Eskandar, E. N., and Cash, S. S. (2010). Coa-

lescence and fragmentation of cortical networks dur-

ing focal seizures. The Journal of neuroscience :

the ofﬁcial journal of the Society for Neuroscience,

30(30):10076–85.

McCulloch, W. S. and Pitts, W. (1943). A logical calculus of

the ideas immanent in nervous activity. The Bulletin

of Mathematical Biophysics, 5(4):115–133.

Merelli, E., Paoletti, N., and Tesei, L. (2012). A multi-level

model for self-adaptive systems. In Kokash, N. and

Ravara, A., editors, Proceedings 11th International

Workshop on Foundations of Coordination Languages

and Self Adaptation, Newcastle, U.K., September 8,

2012, volume 91 of Electronic Proceedings in Theo-

retical Computer Science, pages 112–126. Open Pub-

lishing Association.

Merelli, E., Pettini, M., and Rasetti, M. (2014). Topology

driven modeling: the IS metaphor. Natural Comput-

ing, pages 1–10.

Miller, C. B. and Giles, C. L. (1993). Experimental com-

parison of the effect of order in recurrent neural net-

works. International Journal of Pattern Recognition

and Artiﬁcial Intelligence, 7(04):849–872.

Minsky, M. and Papert, S. (1988). Perceptrons: An intro-

duction to computational geometry. cdsweb.cern.ch.

Monner, D. and Reggia, J. A. (2012). A generalized lstm-

like training algorithm for second-order recurrent neu-

ral networks. Neural Networks, 25:70–83.

Piangerelli, M., Ciavarro, M., Paris, A., Marchetti, S., Cris-

tiani, P., Puttilli, C., Torres, N., Benabid, A. L., and

Romanelli, P. (2014). A fully-integrated wireless sy-

stem for intracranial direct cortical stimulation, real-

time electrocorticography data trasmission and smart

cage for wireless battery recharge. Frontiers in Neu-

rology, 5(156).

Salehie, M. and Tahvildari, L. (2009). Self-adaptive soft-

ware: Landscape and research challenges. ACM

Trans. Auton. Adapt. Syst., 4(2):14:1–14:42.

Sporns, O., Chialvo, D. R., Kaiser, M., and Hilgetag, C. C.

(2004). Organization, development and function of

complex brain networks. Trends in cognitive sciences,

8(9):418–25.

van den Heuvel, M. P. and Sporns, O. (2011). Rich-club

organization of the human connectome. The Journal

of neuroscience : the ofﬁcial journal of the Society for

Neuroscience, 31(44):15775–86.

RNN-basedModelforSelf-adaptiveSystems-TheEmergenceofEpilepsyintheHumanBrain

361