Predicting Wrist Movement Trajectory from Ipsilesional ECoG in

Chronic Stroke Patients

Martin Sp

uler

, Wolfgang Rosenstiel

and Martin Bogdan

1,2

Wilhelm-Schickard-Institute for Computer Science, University of T

ubingen, Sand 13, 72076 T

ubingen, Germany

Computer Engineering, University of Leipzig, Augustusplatz 10, 04109 Leipzig, Germany

Keywords:

Brain-Computer Interface (BCI), Brain-Machine Interface (BMI), Stroke, Trajectory Prediction, Electrocor-

ticography (ECoG), Canonical Correlation Analysis (CCA).

Abstract:

Recently, there have been several approaches to utilize a Brain-Computer Interface (BCI) for chronic stroke

patients. The prediction of movement trajectory based on recorded brain activity could thereby help to improve

BCI-guided stroke rehabilitation or could be used for control of an assistive device, like an orthosis or a robotic

arm. One problem in predicting movement trajectory in stroke patients are compensatory movements, which

make it difﬁcult to link speciﬁc brain activity to movement intention. In this paper we compare different

methods for trajectory prediction and show how Canonical Correlation Analysis (CCA) can be used to predict

movement trajectories. Based on the results, we argue that the resulting trajectory prediction is closer to

the actual movement intention. We further show how the transformation matrices obtained by CCA can be

interpreted and discuss how this interpretation might be useful to get information regarding compensatory

movements in stroke and the underlying patterns of brain activity.

1 INTRODUCTION

More than 80 % of the patients surviving a stroke are

affected by hemiparesis (Cramer et al., 1997) and in

30 % to 66 % of those hemiparetic stroke patients

the paretic arm remains without function when mea-

sured 6 months after stroke (Kwakkel et al., 2003).

Brain-Computer Interface (BCI) technology might

help those patients either by using a BCI as an assis-

tive device to compensate the missing motor function

(Yanagisawa et al., 2011) or as a tool for rehabilita-

tion.

The use of BCI for stroke rehabilitation has been

particularly prominent in the last time (Buch et al.,

2008; Broetz et al., 2010; Ramos-Murguialday et al.,

2013; Sp

uler et al., 2014). In this neurorehabilitation

approach, the patients’ intention to move is coupled

with haptic feedback given through an orthosis mov-

ing the paretic limb (Buch et al., 2008). Since the

connection between the sensorimotor cortex and the

peripheral muscles is disrupted by stroke, a coinci-

dent activation of the primary motor cortex and the

sensory feedback loop may induce Hebbian plasticity

and thus support functional recovery (Silvoni et al.,

2011).

Stroke patients tend to perform compensatory

movements (Cirstea and Levin, 2000), which can be a

problem when using BCI feedback for stroke rehabili-

tation, since compensatory movements produce brain

activity which is unrelated to the intended movement

(Lee et al., 2009) but inadvertently inﬂuences BCI

feedback. Therefore it would be beneﬁcial if brain

activity related to compensatory movements could be

separated from the activity related to the intended

movement and only activity related to the intended

movement is feedbacked by the BCI.

In this paper we evaluate different methods for

the prediction of wrist movement trajectory based

on ipsilesional Electrocorticography (ECoG) data in

chronic stroke patients. A special emphasis is given

on the use of Canonical Correlation Analysis (CCA)

for this purpose. While CCA has been previously

used for SSVEP BCIs (Bin et al., 2009), c-VEP BCIs

(Sp

uler et al., 2012), as well as general spatial ﬁltering

method for classiﬁcation of evoked or event-related

potentials (Sp

uler et al., 2013), we show in this paper

how it can also be used for trajectory prediction and

extraction of movement components from the trajec-

tory data, which may help to feedback brain activity

related to the true movement intention.

Spüler M., Rosenstiel W. and Bogdan M..

Predicting Wrist Movement Trajectory from Ipsilesional ECoG in Chronic Stroke Patients.

DOI: 10.5220/0005165200380045

In Proceedings of the 2nd International Congress on Neurotechnology, Electronics and Informatics (NEUROTECHNIX-2014), pages 38-45

ISBN: 978-989-758-056-7

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 METHODS

In this section we describe the methods we evalu-

ated for the prediction of the movement trajectory, the

evaluation process itself, as well as the ECoG data

used for evaluation.

Since the use of Canonical Correlation Analysis

yields some particularly interesting results, we will

explain the CCA method and its application in more

detail.

2.1 Canonical Correlation Analysis

(CCA)

CCA is a multivariate statistical method developed

by H. Hotelling (Hotelling, 1936). When having

two datasets, which may have some underlying cor-

relations, CCA can be used to ﬁnd linear transfor-

mations for these two datasets, which maximize the

correlation between the transformed datasets. As-

suming there are two multidimensional datasets X

and Y with p variables in X = (X

, X

, ..., X

)

and

q ≤ p variables in Y = (Y

, ...,Y

)

and their trans-

formed datasets U = W

X = (U

, ...,U

)

and

V = W

Y = (V

, ...,V

)

. CCA can be used to

ﬁnd the two transformations W

and W

, which maxi-

mize the canonical correlation ρ

∗

between the canon-

ical variables U

and V

∗

cov(U

)

var(U

)var(V

)

(1)

The linear transformations W

and W

are selected

so that their variance equals one, while they are un-

correlated to all other canonical variables.

var(U

) = var(V

) = 1 (2)

cov(U

) = cov(U

) = 0 , ∀i 6= j (3)

2.1.1 CCA and Linear Regression

A traditional regression can be formulated as having

a multidimensional dataset X with dimensions n × p

containing n observations of p variables and another

dataset Y with dimensions n × 1 containing the de-

pendent variable. A linear regression tries to model

the relationship between X and Y by ﬁnding a weight

vector W with dimensions p ×1 so that

= X

W + ε

(4)

with ε

being the error term which should be minimal.

Thereby one can use W to predict Y

based on the

observations contained in X.

= XW (5)

In the case of an ordinary least squares regression,

this problem is solved by ﬁnding a W that minimizes

the sum of the squared differences between the pre-

dicted Y

and the observed Y . With

being the eu-

clidean distance, the problem can be written as:

minkY −Y

= kXW −Y

(6)

CCA can also be used to solve a regression prob-

lem. Applying CCA to X and Y , the method tries to

ﬁnd a transformation W

that maximized the correla-

tion

ρ =

)(W

)

(7)

The results is W

being a weight vector with dimen-

sions p × 1 and W

being a scalar, which can be used

to predict Y with

= XW ·W

−1

(8)

Since CCA only maximizes the correlation, CCA can

only be used for regression methods under the con-

dition that X and Y have a mean of 0. If this condi-

tion holds, CCA delivers results similar to other linear

regression, as we will see later in this paper. Rela-

tionships between least squares and CCA have been

established earlier in the literature. (Hastie et al.,

1995) found CCA to be equivalent to Fisher Linear

Discriment Analysis in a binary-class case, which in

turn was found to be equivalent to CCA in this case

(Bishop et al., 2006). (Sun et al., 2008) showed

that CCA can be formulated as least squares problem

which can be used to introduce regularized CCA and

sparse CCA (using L1-norm regularization).

2.1.2 CCA and Component Analysis

While we have shown the relationship between CCA

and linear (least squares) regression, there is also

a distinct relationship between CCA and methods

for component analysis like independent component

analysis (ICA) and principal component analysis

(PCA).

If CCA is used with a multidimensional dataset

Y , the resulting transformation matrix W

can be used

as transformation matrix that separates the dataset Y

in different components (called canonical variables

in the context of CCA). Due to the constraints how

CCA selects W

(see equations 2 and 3), the result-

ing components are uncorrelated, which is also the

case for ICA and PCA. Therefore, CCA can be seen

as a method that extracts components V from Y, with

the components V being maximally correlated to U =

PredictingWristMovementTrajectoryfromIpsilesionalECoGinChronicStrokePatients

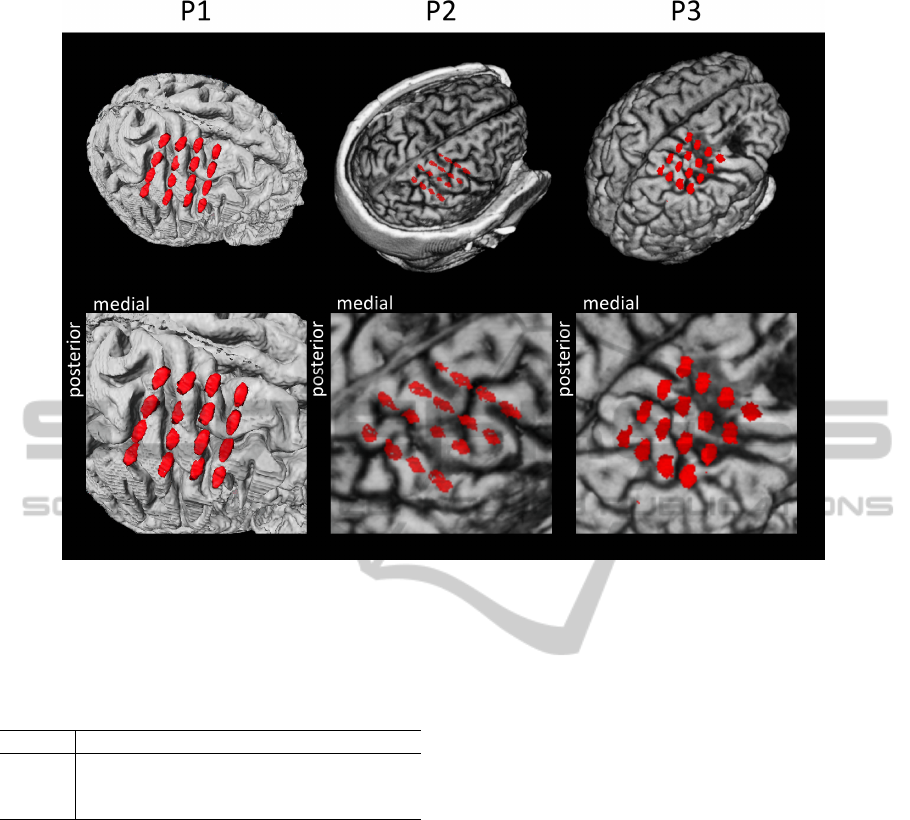
Figure 1: Locations of the epidurally implanted ECoG electrodes. Patients were implanted with 4 strips with 4 electrodes

each. MRI images are reproduced from a previous publication (Walter et al., 2012).

Table 1: Demographic data for the three chronic stroke pa-

tients: Age, Sex, Fugl-Meyer Score for upper extremity

(FMA, max 30), wrist (FMB, max 10), hand (FMC, max

14) and the time since insult (TSI) in month.

Patient Age Sex FMA FMB FMC TSI

P1 63 f 9 0 0 71

P2 56 m 19 3 1 80

P3 52 m 13 6 2 159

2.2 ECoG Data

2.2.1 Patient Description

The ECoG data used in this study was recorded from

3 patients who suffered from left-sided chronic hand-

paresis due to stroke. The patients took part in a long-

term investigational study for motor cortex stimula-

tion with epidural implants concurrent to rehabilita-

tion training to improve upper limb motor function

after stroke. The study protocol was approved by the

local ethics committee (Faculty of Medicine, Univer-

sity Hospital T

ubingen) and included an initial four

week evaluation period immediately after implanta-

tion of the ECoG grids to investigate patients individ-

ual cortical physiology for optimization of stimula-

tion location and paradigms. An overview of the pa-

tients’ demographic data and the Fugl-Meyer scores

(Fugl-Meyer et al., 1975) for wrist movement (FMB)

are shown in table 1.

Each of the 3 patients was epidurally implanted

with 16 platinum disk electrodes (Medtronic, Inc.)

with a diameter of 4 mm, which were arranged in 4

strips with 4 electrodes each. The strips were placed

in a grid-like fashion with a center-to-center distance

of 1 cm. Although technically these are 4 strips, we

will refer to it as one grid. These grids were placed

above the hand area of the ipsilesional motor cortex

and also covered premotor and sensory areas. The

location of the grids are shown in ﬁgure 1. More

detailed information about the patients can be found

in a previous publication (Walter et al., 2012). Data

recorded during that evaluation period was used for

the evaluation of the method presented in this paper.

2.2.2 Task Description

During the aforementioned evaluation period, the pa-

tients also participated in a robot-assisted stroke reha-

bilitation program and ECoG data was recorded dur-

ing the performed exercises. Each of the patients par-

ticipated in 10 to 20 sessions performed on differ-

ent days in which they had to repeat wrist extension

and wrist ﬂexion several times using their paretic arm.

NEUROTECHNIX2014-InternationalCongressonNeurotechnology,ElectronicsandInformatics

On average 8 minutes of wrist extension/ﬂexion were

recorded per session.

The degree to which the patients were able to

perform extension/ﬂexion varied, but movement was

supported by an upper limb rehabilitation robot (Ho-

coma Armeo Spring), which removed gravitational

effects. Further, the robot allowed movement along

7 degrees of freedom (DOF) with the angle of the 7

joints being constantly recorded.

Although the patients were instructed to do a wrist

extension/ﬂexion (needing only 1 DOF), movement

along several DOF was visible due to coactivation

and compensatory movements resulting from stroke.

Therefore, the performed (and recorded) trajectory

not matches the actual intended movement trajectory

and also there is a movement trajectory present for the

other DOF, where no movement was intended.

2.3 Data Processing and Feature

Extraction

ECoG signals were recorded with Brainamp DC

(Brain Products GmbH, Munich, Germany) ampli-

ﬁers at a sampling rate of 1000 Hz and a high-pass

ﬁlter at 0.16 Hz. After recording, the signal was re-

referenced to the common average and a notch ﬁlter

at 50 Hz was applied to ﬁlter out power line noise. To

estimate the power spectrum we used the maximum

entropy method (Burg, 1967) with a model order of

50. The power spectrum was estimated for each chan-

nel in the range from 1 to 500 Hz with a bin width of

4 Hz and the logarithm function was applied to each

value.

To reduce dimensionality of the input space, we

performed a feature selection based on R

values

(Sp

uler et al., 2011) and selected the 50 features

which had the highest values. In the end, those fea-

tures served as input to train a model (using either a

regression method or CCA) to predict movement tra-

jectory.

2.4 Trajectory Prediction

To evaluate which method is suited best for prediction

of movement trajectory, we used the following ﬁve

methods:

1. (L1 reg) Lasso regression: Linear regression with

L1 Norm regularisation using the regularisation

parameter λ = 0.1.

2. (L2 reg) Ridge regression: Linear regression with

L2 Norm regularisation using the regularisation

parameter λ = 0.1.

3. (SVR) Support Vector Regression with a linear

kernel or a radial basis function (RBF) kernel.

For implementation we used LibSVM (Chang and

Lin, 2011) with default kernel parameters and the

hyperparameter C=1.

4. (CCA) Canonical Correlation Analysis for the

prediction of movement components. A more de-

tailed explanation how we applied CCA will be

presented later (see section 2.4.1).

5. (PCA + L2 reg) Since CCA was not used to

predict the actual wrist movement trajectory, but

to predict movement components identiﬁed by

CCA, we also used Principal Component Analysis

(PCA) (Dunteman, 1989) on the recorded move-

ment data (7 degrees of freedom) to obtain move-

ment components that better match the movement

intention of the stroke patients. The principal

components with the highest variance was used

for trajectory prediction by using a ridge regres-

sion as explained previously.

2.4.1 CCA to Predict Movement Components

Based on ECoG Data

We have previously shown that the calculation of W

can be seen as a linear regression, where W

is used

to predict a variable. We have also shown that the

calculation of W

can be seen as a form of component

analysis, where CCA transforms the dataset Y into un-

correlated components. When both datasets X and Y

are multidimensional both aspects have to be consid-

ered and the application of CCA can be seen as an

extraction of components and a regression to predict

those components. Both is done by CCA in one step.

When applying CCA to the ECoG data (as X) and

movement trajectory data (as Y ), we can use CCA to

ﬁnd movement components in the trajectory data and

do a regression to predict those movement compo-

nents based on the ECoG data. The reasoning behind

this approach is that the performed (and recorded)

trajectory differs from intended movement trajectory

due to compensatory movements and the stroke pa-

tients not being able to properly perform the intended

movement. With the extraction of trajectory compo-

nents, we hope to ﬁnd components which are closer

to the actual intended movement trajectory. In this

work we always used the ﬁrst component extracted

by CCA.

2.5 Performance Evaluation

To evaluate the performance of the different meth-

ods for trajectory prediction, we used a 5-fold cross-

validation procedure to make sure that training and

PredictingWristMovementTrajectoryfromIpsilesionalECoGinChronicStrokePatients

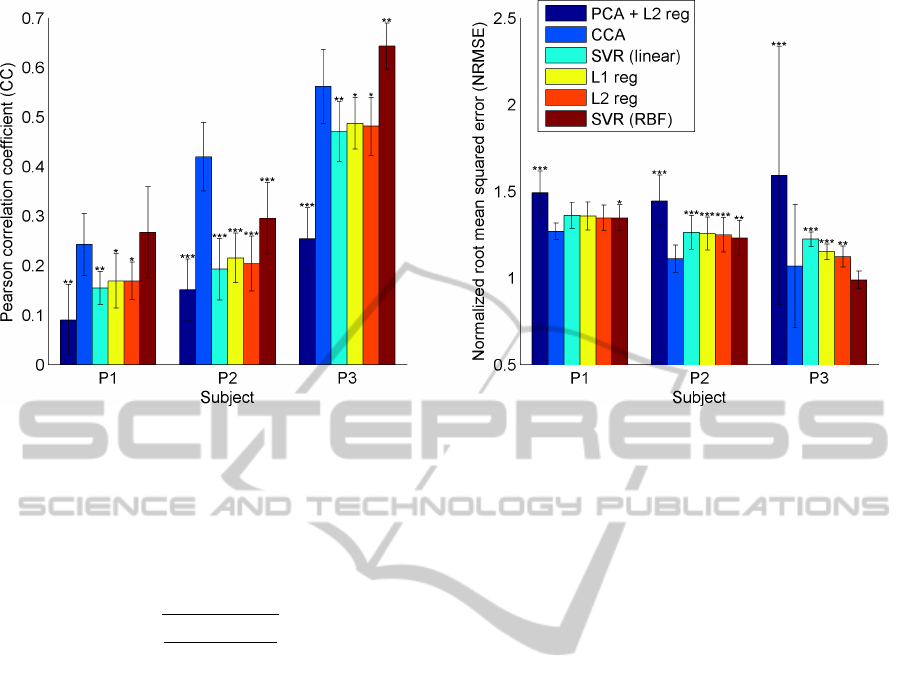
Figure 2: Performance (NRMSE and CC) for different methods for trajectory prediction averaged over all sessions for one

subject. The error bars indicate the standard deviation. Asteriks denote if there is a signiﬁcant difference between the method

and CCA, with

∗

p < 0.05,

∗∗

p < 0.01,

∗∗∗

p < 0.001 (Wilcoxon ranksum test).

test data do not overlap. To quantify the performance

of the methods, we used Pearson’s correlation coefﬁ-

cient (CC) an the normalized root mean squared error

(NRMSE), which we deﬁned as

NRMSE =

∑

t=1

( ˆy

− y

)

· var(y)

−1

(9)

with y

being the actual and ˆy

being the predicted

value. var(y) denotes the variance of the actual tra-

jectory. Since the trajectory values are different de-

pending if PCA or CCA are used, the normalization

is important to compare the RMSE between the meth-

ods.

3 RESULTS

3.1 Performance of Trajectory

Prediction

On average CCA performed best with an average

CC = 0.41 and an average NRMSE = 1.15. While

CCA performs consistently better than the other lin-

ear methods, a Support Vector Regression (SVR) with

a RBF-kernel has a signiﬁcantly (p < 0.01) higher CC

for subject P3. The results are show in ﬁgure 2 in

more detailed. For each subject and method, the re-

sults are averaged over all session with the standard

deviation being indicated by error bars and the signif-

icance between each of the methods and CCA being

assessed by a two-sided Wilcoxon ranksum test.

3.2 Interpretation of CCA

Transformation Matrices

Due to the nature of CCA, the transformation matri-

ces W

and W

could be used for some neurophysio-

logical interpretation of the data. While W

is used to

predict the movement trajectory, it shows which elec-

trodes and which frequency ranges are important for

the prediction. Thereby one can infer where (location

and frequency) movement-related activity is present.

is used to calculate the movement components and

in turn can be used to infer which joints (represented

by the DOFs in our data) are active during an in-

tended wrist movement. This could be used to gain

more knowledge regarding the compensatory move-

ment patterns of stroke patients.

Figure 3 shows the weights using a linear regres-

sion to visualize which electrodes and frequencies are

used to predict the recorded wrist movement trajec-

tory, as well as the recorded and predicted wrist move-

ment trajectory for one exemplary session. Figure 3

also shows the R

-values (Sheikh et al., 2003) indicat-

ing which features (electrode × frequency) correlate

best with the trajectory.

Figure 4 shows the weights of the W

and W

(for

the ﬁrst movement component) when using CCA on

one exemplary session. As well as the actual and pre-

dicted movement trajectory.

When comparing both ﬁgures, the activity pattern

obtained by CCA (ﬁgure 4.A) is more localized than

the one obtained by a linear regression (ﬁgure 3.A).

Furthermore, the weights of W

(ﬁgure 4.B) yield in-

NEUROTECHNIX2014-InternationalCongressonNeurotechnology,ElectronicsandInformatics

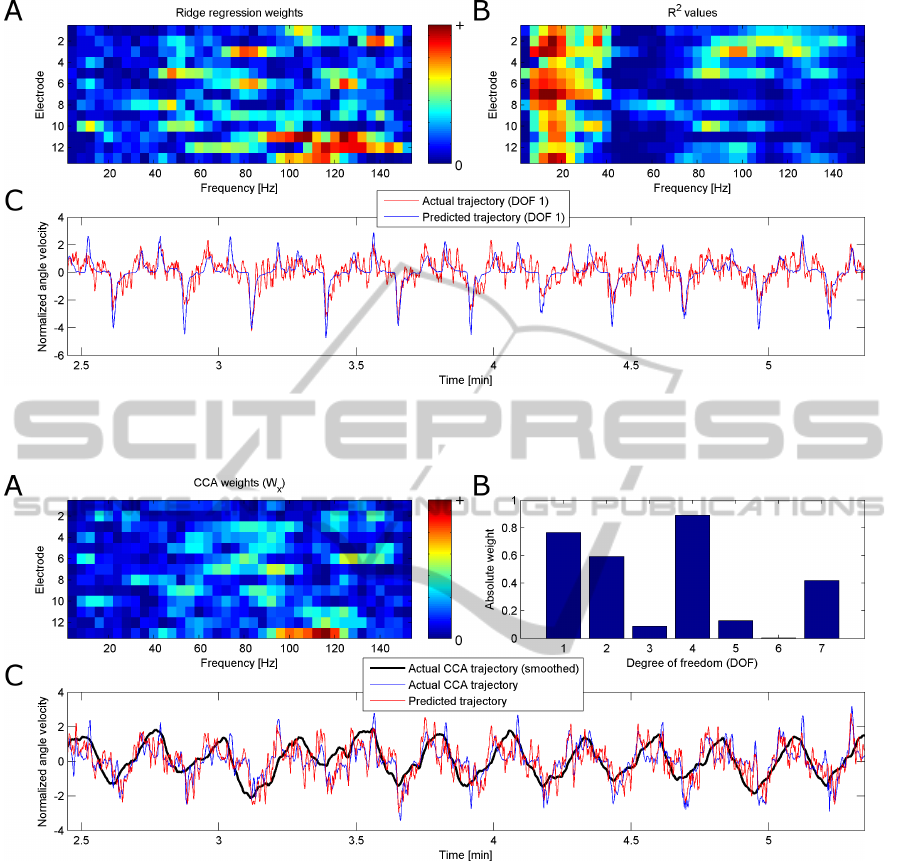
Figure 3: A: Absolute weights from ridge regression for each feature (frequency × electrode) used in trajectory prediction.

B: R

values indicating high correlation between each feature and the trajectory C: Actual and predicted trajectory of the

movement component calculated by ridge regression.

Figure 4: A: Absolute weights from CCA for each feature (frequency × electrode) used in trajectory prediction of the ﬁrst

movement component. B: Absolute weights for each DOF to calculate the movement component. C: Actual and predicted

trajectory of the movement component calculated by CCA. The smoothed trajectory is only shown for better display purposes

and was not used for trajectory prediction or performance evaluation.

formation, which DOFs are affected by the intended

wrist movement, thereby showing the coactivation

pattern present during the intended wrist movement.

Figure 3.C shows the actual and the predicted

wrist movement trajectory using linear regression,

while ﬁgure 4.C shows the predicted and actual move-

ment trajectory obtained by CCA. When comparing

the results from CCA with the results using a lin-

ear regression, the trajectory obtained by CCA seems

more noisy but more natural and more representative

of the true intended movement.

4 DISCUSSION

In this paper we have compared different methods

for the trajectory prediction from ECoG in stroke pa-

tients. The fact that ECoG can be used for trajectory

prediction was shown in several studies for subjects

with an intact sensorimotor system. In (Schalk et al.,

2008) average CC were approximately between 0.22

and 0.71, in (Pistohl et al., 2008) CCs between 0.3

and 0.6 were reached and performance in later stud-

ies yielded CCs in a similar range. (Nakanishi et al.,

PredictingWristMovementTrajectoryfromIpsilesionalECoGinChronicStrokePatients

2013) have shown that it is also possible to predict

movement trajectory in stroke patients from ipsile-

sional ECoG. With an average CC ranging between

0.44 and 0.73 the performance obtained by Nakan-

ishi et al. is similar to the results obtained in earlier

studies with subjects without motor dysfunction. We

could reproduce this ﬁnding in our work and were

able to decode the trajectory with an average CC be-

tween 0.24 and 0.64 depending on the subject, which

is similar to the results by (Nakanishi et al., 2013).

It should be noted that there seems to be a nega-

tive correlation between the Fugl-Meyer (FM) Score

regarding wrist movement and the accuracy of wrist

trajectory prediction, since the patient with the lowest

FM score (indicating a high wrist motor dysfunction)

had the lowest CC and vice versa. Although it seems

reasonable to assume that wrist movement trajectory

is harder to decode for patients whose motor system

is more damaged by stroke, the current dataset (with

only three patients measured) is too small to draw any

signiﬁcant conclusions.

Regarding the comparison of different prediction

methods for wrist trajectory prediction, we found

CCA and Support Vector Regression (SVR) with an

RBF kernel to perform best. While CCA performed

on average slightly better than SVR, the use of CCA

has either advantages or disadvantages compared to

SVR, depending on the point of view. While SVR

predicts the trajectory of a speciﬁc joint, CCA pre-

dicts the trajectory of a component. So obviously

CCA cannot be used when the aim is the prediction

of a certain joint or a certain movement direction.

But in case of stroke rehabilitation or orthotic con-

trol, one could also use the components predicted by

CCA to give the user feedback using multiple joints at

once, which would allow for a more natural feedback.

This gets clearer when looking at the movement tra-

jectories. The performed (and recorded) wrist move-

ment trajectory looks unnatural and choppy, which is

caused by hemiparesis and compensatory movements

due to stroke. The movement trajectory obtained by

CCA, although being more noisy, resembles much

better the intended wrist extension and ﬂexion tra-

jectory. Thereby we argue that CCA is not only bet-

ter suited for trajectory decoding than other methods,

but also allows to predict the real movement intention

of the patient instead of the performed and impaired

movement of the stroke patient. Based on these re-

sults, one could interpret the transformation matrices

to infer knowledge regarding the participation of dif-

ferent joints in compensatory movements and which

parts of the brain signal yield information regarding

the compensatory movement and the intended move-

ment. Although we did not demonstrate this aspect of

CCA in detail, we think that CCA is a potential tool

in this ﬁeld with possible applications beyond the use

for trajectory prediction.

5 CONCLUSION

In this paper we have shown that we are able to

decode wrist movement trajectory from hemiparetic

chronic stroke patients based on ipsilesional ECoG

recordings over their sensorimotor cortex. We have

further compared different methods for trajectory pre-

diction and could show that either SVR (with RBF

kernel) or CCA are the best methods for trajec-

tory prediction, depending on the intended applica-

tion. Further we have outlined how the application

of CCA could be potentially useful to infer infor-

mation regarding compensatory movements, the in-

tended movement trajectory and the underlying brain

activity regarding both.

ACKNOWLEDGMENTS

We thank Florian Grimm and Alireza Gharabghi for

recording the data and making them available for this

study. This work was supported by the European Re-

search Council (ERC 227632-BCCI) and the Baden-

urttemberg Stiftung (GRUENS).

REFERENCES

Bin, G., Gao, X., Yan, Z., Hong, B., and Gao, S.

(2009). An online multi-channel SSVEP-based

brain-computer interface using a canonical correla-

tion analysis method. Journal of Neural Engineering,

6(4):046002.

Bishop, C. M. et al. (2006). Pattern recognition and ma-

chine learning, volume 1. springer New York.

Broetz, D., Braun, C., Weber, C., Soekadar, S., Caria, A.,

and Birbaumer, N. (2010). Combination of brain-

computer interface training and goal-directed physical

therapy in chronic stroke: a case report. Neuroreha-

bilitation and Neural Repair, 24(7):674–679.

Buch, E., Weber, C., Cohen, L., Braun, C., Dimyan,

M., Ard, T., Mellinger, J., Caria, A., Soekadar,

S., Fourkas, A., and Birbaumer, N. (2008). Think

to move: a neuromagnetic brain-computer interface

(BCI) system for chronic stroke. Stroke, 39:910–7.

Burg, J. P. (1967). Maximum entropy spectral analysis. In

37th Annual International Meeting. Society of Explo-

ration Geophysics.

Chang, C.-C. and Lin, C.-J. (2011). Libsvm: a library for

support vector machines. ACM Transactions on Intel-

ligent Systems and Technology (TIST), 2(3):27.

NEUROTECHNIX2014-InternationalCongressonNeurotechnology,ElectronicsandInformatics

Cirstea, M. and Levin, M. F. (2000). Compensatory strate-

gies for reaching in stroke. Brain, 123(5):940–953.

Cramer, S., Nelles, G., Benson, R., Kaplan, J., Parker, R.,

Kwong, K., Kennedy, D., Finklestein, S., and Rosen,

B. (1997). A functional MRI study of subjects recov-

ered from hemiparetic stroke. Stroke, 28(12):2518–

2527.

Dunteman, G. H. (1989). Principal components analysis.

Number 69. Sage.

Fugl-Meyer, A., J

ask

o, L., Leyman, I., Olsson, S., and

Steglind, S. (1975). The post-stroke hemiplegic

patient. a method for evaluation of physical per-

formance. Scandinavian journal of rehabilitation

medicine, 7(1):13–31.

Hastie, T., Buja, A., and Tibshirani, R. (1995). Penalized

discriminant analysis. The Annals of Statistics, pages

73–102.

Hotelling, H. (1936). Relations between two sets of vari-

ates. Biometrika, 28(3/4):321–377.

Kwakkel, G., Kollen, B. J., van der Ground, J., and Prevo,

A. J. (2003). Probability of regaining dexterity in the

ﬂaccid upper limb impact of severity of paresis and

time since onset in acute stroke. Stroke, 34:2181–

2186.

Lee, M. Y., Park, J. W., Park, R. J., Hong, J. H., Son, S. M.,

Ahn, S. H., Cho, Y. W., and Jang, S. H. (2009). Cor-

tical activation pattern of compensatory movement in

stroke patients. NeuroRehabilitation, 25(4):255–260.

Nakanishi, Y., Yanagisawa, T., Shin, D., Fukuma, R.,

Chen, C., Kambara, H., Yoshimura, N., Hirata, M.,

Yoshimine, T., and Koike, Y. (2013). Prediction of

three-dimensional arm trajectories based on ecog sig-

nals recorded from human sensorimotor cortex. PloS

one, 8(8):e72085.

Pistohl, T., Ball, T., Schulze-Bonhage, A., Aertsen, A., and

Mehring, C. (2008). Prediction of arm movement tra-

jectories from ecog-recordings in humans. Journal of

neuroscience methods, 167(1):105–114.

Ramos-Murguialday, A., Broetz, D., Rea, M., L

aer, L., Yil-

maz,

O., Brasil, F. L., Liberati, G., Curado, M. R.,

Garcia-Cossio, E., Vyziotis, A., et al. (2013). Brain-

machine interface in chronic stroke rehabilitation: A

controlled study. Annals of neurology, 74(1):100–108.

Schalk, G., Miller, K., Anderson, N., Wilson, J., Smyth, M.,

Ojemann, J., Moran, D., Wolpaw, J., and Leuthardt,

E. (2008). Two-dimensional movement control us-

ing electrocorticographic signals in humans. J Neural

Eng, 5(1):75–84.

Sheikh, H., McFarland, D. J., Sarnacki, W. A., and Wolpaw,

J. R. (2003). Electroencephalographic (eeg)-based

communication: Eeg control versus system perfor-

mance in humans. Neuroscience letters, 345(2):89–

92.

Silvoni, S., Ramos-Murguialday, A., Cavinato, M., Vol-

pato, C., Cisotto, G., Turolla, A., Piccione, F., and

Birbaumer, N. (2011). Brain-computer interface in

stroke: a review of progress. Clinical EEG and Neu-

roscience, 42(4):245–252.

uler, M., Rosenstiel, W., and Bogdan, M. (2011). A

fast feature selection method for high-dimensional

MEG BCI data. In Proceedings of the 5th Int. Brain-

Computer Interface Conference, pages 24–27, Graz.

uler, M., Rosenstiel, W., and Bogdan, M. (2012). On-

line adaptation of a c-VEP Brain-Computer Interface

(BCI) based on Error-related potentials and unsuper-

vised learning. PloS one, 7(12):e51077.

uler, M., Walter, A., Ramos Murguialday, A., Naros, G.,

Birbaumer, N., Gharabaghi, A., Rosenstiel, W., and

Bogdan, M. (2014). Decoding of motor intentions

from epidural ECoG recordings in severely paralyzed

chronic stroke patients. Journal of Neural Engineer-

ing. accepted.

uler, M., Walter, A., Rosenstiel, W., and Bogdan, M.

(2013). Spatial Filtering Based on Canonical Corre-

lation Analysis for Classiﬁcation of Evoked or Event-

Related Potentials in EEG Data. IEEE Transactions

on Neural Systems and Rehabilitation Engineering.

Sun, L., Ji, S., and Ye, J. (2008). A least squares formu-

lation for canonical correlation analysis. In Proceed-

ings of the 25th international conference on Machine

learning, pages 1024–1031. ACM.

Walter, A., Murguialday, A. R., Sp

uler, M., Naros, G., Le

ao,

M. T., Gharabaghi, A., Rosenstiel, W., Birbaumer, N.,

and Bogdan, M. (2012). Coupling BCI and corti-

cal stimulation for brain-state-dependent stimulation:

methods for spectral estimation in the presence of

stimulation after-effects. Frontiers in neural circuits,

Yanagisawa, T., Hirata, M., Saitoh, Y., Goto, T., Kishima,

H., Fukuma, R., Yokoi, H., Kamitani, Y., and

Yoshimine, T. (2011). Real-time control of a pros-

thetic hand using human electrocorticography signals:

technical note. Journal of neurosurgery, 114(6):1715–

1722.

PredictingWristMovementTrajectoryfromIpsilesionalECoGinChronicStrokePatients