
Applying Information-theoretic and Edit Distance Approaches
to Flexibly Measure Lexical Similarity
Thi Thuy Anh Nguyen and Stefan Conrad
Institute of Computer Science, Heinrich-Heine-University D¨usseldorf, Universit¨atsstr. 1, D-40225 D¨usseldorf, Germany
Keywords:
Information-theoretic Model, Feature-based Measure, String-based Measure, Similarity.
Abstract:
Measurement of similarity plays an important role in data mining and information retrieval. Several tech-
niques for calculating the similarities between objects have been proposed so far, for example, lexical-based,
structure-based and instance-based measures. Existing lexical similarity measures usually base on either n-
grams or Dice’s approaches to obtain correspondences between strings. Although these measures are efficient,
they are inadequate in situations where strings are quite similar or the sets of characters are the same but their
positions are different in strings. In this paper, a lexical similarity approach combining information-theoretic
model and edit distance to determine correspondences among the concept labels is developed. Precision, Re-
call and F-measure as well as partial OAEI benchmark 2008 tests are used to evaluate the proposed method.
The results show that our approach isflexible and has some prominent features compared to other lexical-based
methods.
1 INTRODUCTION
The similarity measures play an important role and
are applied in many well-known areas, such as data
mining and information retrieval. Several techniques
for determining the similarities between objects have
been proposed so far, for example, lexical-based,
structure-based and instance-based measures. Among
these, lexical similarity metrics find correspondences
between given strings. These measures are usually
applied in ontology matching systems, information
integration, bioinformatics, plagiarism detection, pat-
tern recognition and spell checkers. The lexical tech-
niques are based on the fact that the more the charac-
ters in strings are similar, the more the similarity val-
ues increase. Existing lexical-based measures usually
based on either n-grams or Dice’s approaches. The
advantage of these measures is a good performance.
Moreover, n-grams metrics could be extended in case
the parameter n is adjusted. However, they have the
disadvantage that they do not return reasonable re-
sults in some situations where strings are quite similar
or the sets of characters are the same but their posi-
tions are different in strings. To deal with this prob-
lem, a similarity approach based on the combination
of features-based and element-based measures is pro-
posed. In particular, it is combined from information-
theoretic model and edit-distance measure. Conse-
quently, commonand different properties with respect
to characters in strings as well as editing and non-
editing operations are considered.
The remainder of this paper is organized as fol-
lows. Section 2 overviews the related lexical mea-
sures. In section 3, a similarity measure taking into
account text strings is proposed. In section 4, we de-
scribe our experimental results, give an evaluation as
well as a discussion of our measure and compare it
with other approaches applying Precision, Recall and
F-measure. Finally, conclusions and future work are
presented in section 5.
2 RELATED WORK
The lexical similarity measures are usually used to
match short strings such as entity names in ontologies,
protein sequences and letter strings. In the following
subsections, a brief description of these measures is
presented.
2.1 Dice Coefficient
Dice coefficient (also called coincidence index) com-
putes the similarity of two species A and B as the ratio
of two times the size of the intersection divided by the
505
Nguyen T. and Conrad S..
Applying Information-theoretic and Edit Distance Approaches to Flexibly Measure Lexical Similarity.
DOI: 10.5220/0005170005050511
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (SSTM-2014), pages 505-511
ISBN: 978-989-758-048-2
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

total number of samples in these sets and is given as
(Dice, 1945):
sim(A, B) =
2h
a+ b
(1)
where A and B are distinctive species, h is the number
of common samples in A and B, and a, b are the num-
bers of samples in A and B, respectively. Accordingly,
the higher the number of common samples in A and
B, the more their similarity increases.
Dice’s measure can be described as
sim(A, B) =
2|A∩ B|
|A| + |B|
=
2|A∩ B|
2|A∩ B| + |A\B| + |B\A|
(2)
2.2 N-grams Approach
N-grams of a sequence are all subsequences with a
length equals to n. The items in these subsequences
can be characters, tokens in contexts or signals in
speech corpus. For example, n-grams of the string
ontology with n = 3 consist of {ont, nto, tol, olo, log,
ogy}. In case of n-grams of size 1, 2 or 3 they are
also known as unigram, bigram or trigram, respec-
tively. Let |c
1
|, |c
2
| are lengths of strings c
1
and c
2
,
respectively, the similarity between these strings can
be presented as (Euzenat and Shvaiko, 2013):
sim(c
1
, c
2
) =
|ngram(c
1
) ∩ ngram(c
2
)|
min(|c
1
|, |c
2
|) − n+ 1
(3)
The Eq. (3) can be reformulated as follows:
sim(c
1
, c
2
) =
|ngram(c
1
) ∩ ngram(c
2
)|
min(|ngram(c
1
)|, |ngram(c
2
)|)
(4)
N-grams method is widely used in natural lan-
guage processing, approximate matching, plagiarism
detection, bioinformatics and so on. Some measures
applied n-grams approach to calculate the similar-
ity between two objects (Kondrak, 2005; Algergawy
et al., 2008; Ichise, 2008). The combination of Dice
and n-grams methods in (Algergawy et al., 2008;
Kondrak, 2005) to match two given concepts in on-
tologies is shown below.
2.3 Kondrak’s Methods
Kondrak (Kondrak, 2005) develops and uses a notion
of n-grams similarity for calculating the similarities
between words. In this method, the similarity can be
written as
sim(c
1
, c
2
) =
2|ngram(c
1
) ∩ ngram(c
2
)|
|ngram(c
1
)| + |ngram(c
2
)|
(5)
As can be seen in Eq. (2) and Eq. (5), Kondrak’s
method is a specific case for Dice’s metric in which
the samples correspond to n-grams.
2.4 Algergawy’s Methods
Matching two ontologies is presented by Algergawy
et al. (Algergawy et al., 2008), in which three similar-
ity methods are combined in a name matcher phase.
Furthermore, Dice’s expression is implemented to ob-
tain similarities between concepts by using trigrams.
Particularly, this measure applies the set of trigrams in
compared strings c
1
and c
2
instead of using the num-
ber of samples in datasets:
sim(c
1
, c
2
) =
2|tri(c
1
) ∩tri(c
2
)|
|tri(c
1
)| + |tri(c
2
)|
(6)
where tri(c
1
) and tri(c
2
) are the sets of trigrams in c
1
and c
2
, respectively.
2.5 Jaccard Similarity Coefficient
Jaccard measure (Jaccard, 1912) is developed to find
out the distributionof the flora in areas. The similarity
related to frequency of occurrence of the flora is the
number of species in common to both sets with regard
to the total number of species.
Let A and B be arbitrary sets. Jaccard’s metric can
be normalized and is presented as (Jaccard, 1912)
sim(A, B) =
|A∩ B|
|A∪ B|
=
|A∩ B|
|A∩ B| + |A\B| + |B\A|
(7)
Applying n-grams approach to Jaccard’s measure
leads to the following expression:
sim(c
1
, c
2
) =
|ngram(c
1
) ∩ ngram(c
2
)|
|ngram(c
1
) ∪ ngram(c
2
)|
(8)
As can be seen in equations 5 and 8, Kondrak and
Jaccard measures are quite similar.
2.6 Needleman-Wunsch Measure
The Needleman-Wunsch measure (Needleman and
Wunsch, 1970) is proposed to determine the similari-
ties of the amino acids in two proteins. This measure
pays attention to maximum of amino acids of one se-
quence that can be matched with another. Therefore,
it is used to achieve the best alignment. A maximum
score matrix M(i, j) is built recursively, such that
M(i, j) = max
M(i− 1, j − 1) + s(i, j) Aligned
M(i− 1, j) + g Deletion
M(i, j − 1) + g Insertion
(9)
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
506

where s(i, j) is the substitution score for residues i and
j, and g is the gap penalty.
2.7 Hamming Distance
Hamming distance (Hamming, 1950) only applies to
strings of the same sizes. With this measure, the dif-
ference between two input strings is the minimum
number of substitutions that could have changed one
string into the other. In case of differentstring lengths,
Hamming distance dis(c
1
, c
2
) is modified as (Euzenat
and Shvaiko, 2013):
dis(c
1
, c
2
) =
∑
min(|c
1
|,|c
2
|)
i=1
[c
1
[i] 6= c
2
[i]]
+ ||c
1
| −|c
2
||
max(|c
1
|, |c
2
|)
(10)
where |c
1
|, |c
2
| are string lengths, and c
1
[i], c
2
[i] are
the i
th
characters in two strings c
1
and c
2
, respectively.
Besides using only the operation of substitutions,
the Levenshtein distance applying insertions or dele-
tions for comparing strings of different lengths is pre-
sented in the succeeding section.
2.8 Levenshtein Distance
The Levenshtein distance (also called Edit distance)
(Levenshtein, 1966) is a well-know string metric cal-
culating the amount of differences between two given
strings and then returning a value. This value is the to-
tal cost of the minimum number of operations needed
to transform one string into another. Three types of
operations are used including the substitution of a
character of the first string by a character of the sec-
ond string, the deletion or the insertion of a character
of one string into other. The total cost of the used op-
erations is equal to the sum of the costs of each of the
operations (Nguyen and Conrad, 2013).
Let c
1
and c
2
are two arbitrary strings. The simi-
larity measure for two strings sim(c
1
, c
2
) is described
as (Maedche and Staab, 2002):
sim(c
1
, c
2
) = max
0,
min(|c
1
|, |c
2
|) − ed(c
1
, c
2
)
min(|c
1
|, |c
2
|)
(11)
where |c
1
|, |c
2
| are lengths of strings c
1
and c
2
,
respectively, and ed(c
1
, c
2
) is Levenshtein measure.
Note that the cost assigned to each operation here
equals to 1.
2.9 Jaro-Winkler Measure
The Jaro-Winkler measure (Winkler, 1990) is based
on the Jaro distance metric (Jaro, 1989) to compute
the similarity between two strings. The Jaro-Winkler
measure sim(c
1
, c
2
) between c
1
and c
2
strings can be
defined as follows:
sim(c
1
, c
2
) = sim
Jaro
(c
1
, c
2
) + ip(1− sim
Jaro
(c
1
, c
2
))
(12)
where i is the number of the first common characters
(also known as the length of the common prefix), p
is a constant and is assigned to 0.1 in Winkler’s work
(Winkler, 1990) and sim
Jaro
(c
1
, c
2
) is the Jaro metric,
defined as
sim
Jaro
(c
1
, c
2
) =
(
0 if m = 0
1
3
m
|c
1
|
+
m
|c
2
|
+
m−t
m
otherwise
(13)
In Eq. (13), m is the number of matching charac-
ters and t is the number of transpositions.
2.10 Tversky’s Model
In Tversky’s ratio model (Tversky, 1997), determi-
nation of the similarity among objects is related to
features of these objects. In particular, the similarity
value of object o
1
to object o
2
depends on their shared
and different features, so that
sim(o
1
, o
2
) =
φ(o
1
)∩φ(o
2
)
(φ(o
1
)∩φ(o
2
))+β(φ(o
1
)\φ(o
2
))+γ(φ(o
2
)\φ(o
1
))
(14)
where φ represents the set of features, φ(o
1
) ∩
φ(o
2
) presents common features of both o
1
and o
2
,
φ(o
i
)\φ(o
j
) describes features being held by o
i
but
not in o
j
, (i, j = 1, 2). The parameters β and γ are
adjusted and depend on which features are taken into
account. Therefore, in general this model is asymmet-
ric, it means, sim(o
1
, o
2
) 6= sim(o
2
, o
1
). This model
is also a general approach applied in many matching
functionsin the literature as well as domains (S´anchez
et al., 2012; Pirr´o and Euzenat, 2010).
3 COMBINING INFORMATION -
THEORETIC AND EDIT
DISTANCE MEASURES
3.1 Our Similarity Measure
In this section, a lexical similarity measure is pro-
posed. Our approach is motivated on Tversky’s set-
theoretical model (Tversky, 1997) and Levenshtein
measure (Levenshtein, 1966). We agree that the simi-
larities among entities depend on their commonalities
and differences based on the intuitions in (Lin, 1998).
The well-known metrics applying Tversky’s model
take into account features of compared objects such as
intrinsic information content (Pirr´o and Seco, 2008;
ApplyingInformation-theoreticandEditDistanceApproachestoFlexiblyMeasureLexicalSimilarity
507

Pirr´o and Euzenat, 2010), the number of shared su-
perconcepts (Batet et al., 2011), the number of com-
mon attributes, instances and relational classes (Wang
et al., 2006) in ontologies. In contrast with existing
approaches, the objective of our metric is to focus on
the features in terms of the contents of the characters
and their positions in strings. In particularly, our mea-
sure is related to editing and non-editing operations.
As mentioned earlier, Tversky’s model is a gen-
eral approach considering the common and different
features of objects in which the different features are
represented by their proportions through parameters
β and γ. In our method, a parameter α is added to
the common feature of Eq. (14). Consequently, the
similarity is given by
sim(c
1
, c
2
) =
α(φ(c
1
)∩φ(c
2
))
α(φ(c
1
)∩φ(c
2
))+β(φ(c
1
)\φ(c
2
))+γ(φ(c
2
)\φ(c
1
))
(15)
where the parameters α, β and γ are subjected to a
constraint: α + β + γ = 1. Additionally, the similarity
of two strings should be a symmetric function and the
differences between these strings have the same con-
tribution, the parameters β and γ can be considered to
be equal. Therefore, our measure Lex
sim(c
1
, c
2
) can
be rewritten as
Lex
sim(c
1
, c
2
) =
=
α(φ(c
1
)∩φ(c
2
))
α(φ(c
1
)∩φ(c
2
))+β((φ(c
1
)\φ(c
2
))+(φ(c
2
)\φ(c
1
)))
(16)
where α+ 2β = 1 and α, β 6= 0.
In case α = β = γ =
1
3
, our measure can be written
as
Lex
sim(c
1
, c
2
) =
=
α(φ(c
1
)∩φ(c
2
))
α((φ(c
1
)∩φ(c
2
))+(φ(c
1
)\φ(c
2
))+(φ(c
2
)\φ(c
1
)))
=
φ(c
1
)∩φ(c
2
)
φ(c
1
)∪φ(c
2
)
(17)
which coincides with the Jaccard’s measure.
The representation of the Dice’s approach can be
obtained by setting β = γ =
1
2
α. Indeed,
Lex
sim(c
1
, c
2
) =
=
α(φ(c
1
)∩φ(c
2
))
α(φ(c
1
)∩φ(c
2
))+
1
2
α((φ(c
1
)\φ(c
2
))+(φ(c
2
)\φ(c
1
)))
=
2(φ(c
1
)∩φ(c
2
))
φ(c
1
)+φ(c
2
)
(18)
In this work, features of strings are chosen as the
contents and positions of characters. It is the num-
ber of deletions, insertions and substitutions. More-
over, it uses Levenshtein measure to achieve common
and different values between two strings. The editing
operations can be regarded as the difference, while
non-editing can be reflected on commonalities. These
values are then applied to Tversky’s model.
Accordingly, common features between two
strings are obtained by subtracting the total cost of
the operations needed to transform one string into an-
other from the maximum length of these strings and
is represented as
φ(c
1
) ∩ φ(c
2
) = max(|c
1
|, |c
2
|) − ed(c
1
, c
2
) (19)
The differences between two strings are:
φ(c
1
)\φ(c
2
) = |c
1
| − max(|c
1
|, |c
2
|) + ed(c
1
, c
2
)
(20)
and
φ(c
2
)\φ(c
1
) = |c
2
| − max(|c
1
|, |c
2
|) + ed(c
1
, c
2
)
(21)
respectively.
Our similarity measure for two strings (c
1
, c
2
)
based on Levenshtein measure becomes:
Lex
sim(c
1
, c
2
) =
=
α(max(|c
1
|,|c
2
|)−ed(c
1
,c
2
))
α(max(|c
1
|,|c
2
|)−ed(c
1
,c
2
))+β(|c
1
|+|c
2
|−2max(|c
1
|,|c
2
|)+2ed(c
1
,c
2
))
(22)
where |c
1
|, |c
2
| are lengths of strings c
1
and c
2
,
respectively; ed(c
1
, c
2
) is Levenshtein measure and
α+ 2β = 1.
In case β = γ =
1
2
α, substitution in Eq. (22) yields
Lex
sim(c
1
, c
2
) =
2α(max(|c
1
|, |c
2
|) − ed(c
1
, c
2
))
α(|c
1
| + |c
2
|)
(23)
When the lengths of two strings are the same,
we have max(|c
1
|, |c
2
|) = min(|c
1
|, |c
2
|) = |c
1
| = |c
2
|,
substitution in Eq. (23) yields
Lex sim(c
1
, c
2
) =
min(|c
1
|, |c
2
|) − ed(c
1
, c
2
)
min(|c
1
|, |c
2
|)
(24)
which is similar to the Levenshtein’s measure.
3.2 Properties of Proposed Similarity
Approach
In this section, the properties of proposed similarity
measure are discussed. As can be seen in Eq. (22),
our measure satisfies three properties of a similarity
function as follows (Euzenat and Shvaiko, 2013):
• Positiveness: ∀c
1
, c
2
: Lex
sim(c
1
, c
2
) ≥ 0
Lex
sim(c
1
, c
2
) = 0 if and only if
(max(|c
1
|, |c
2
|) − ed(c
1
, c
2
)) = 0; consequently,
c
1
and c
2
are totally different.
• Maximality:
∀c
1
, c
2
, c
3
: Lex
sim(c
1
, c
1
) ≥ Lex sim(c
2
, c
3
)
In fact, the values of our measure were taken
in the range of [0, 1], Lex
sim(c
1
, c
1
) = 1,
Lex sim(c
2
, c
3
) ≤ 1. Lex sim(c
2
, c
3
) = 1 if
and only if (|c
2
| + |c
3
| − 2max(|c
2
|, |c
3
|) +
2ed(c
2
, c
3
)) = 0, it means c
2
and c
3
are similar.
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
508

• Symmetry: ∀c
1
, c
2
: sim(c
1
, c
2
) = sim(c
2
, c
1
)
In order to evaluate the performance of our lexical
similarity measure, experiments and results are shown
in the following section.
4 EXPERIMENTS AND
DISCUSSIONS
We use ontologies taken from the OAEI benchmark
2008
1
to test and evaluate the performance of our
measure and other ones through comparing between
their output and reference alignments. This bench-
mark consists of ontologies modified from the ref-
erence ontology 101 by changing properties, using
synonyms, extending structures and so on. Since the
measures here concentrate on calculating the string-
based similarity, only ontologies relating to modi-
fied labels and the real bibliographic ontologies are
chosen to evaluate. Consequently, the considered
ontologies consist of 101, 204, 301, 302, 303 and
304. Actually, these chosen ontologies are quite
suitable for the validation and comparison among
Needleman-Wunsch, Jaro-Winkler, Levenshtein, nor-
malized Kondrak’s method combining Dice and n-
grams approaches, with using the same classical met-
rics. These classical metrics are Precision, Recall and
F-measure and can be shown as in Eq. (25).
Precision =
No. correct f ound correspondences
No. found correspondences
Recall =
No.
correct f ound correspondences
No. existing correspondences
F − measure =
2∗ Precision∗ Recall
Precision+ Recall
(25)
Precision, Recall, F-measure and their average
values of six pairs of ontologies are presented in Table
1. Note that these results in Table 1 are obtained by
means of thresholds changed for nine different values
from 0.5 to 0.9 with the increment of 0.05; in addition,
two parameters including α = 0.2 and β = 0.4 were
applied. Based on each threshold value, the align-
ments are achieved for five participants. Then average
Precision, Recall and F-measure for all these thresh-
olds are calculated.
In Table 1, our measure gives premier value of av-
erage F-measure compared to those of other methods.
It clearly indicates that our approach is more effec-
tive than the others. Moreover, both our measure and
Levenshtein’s are slightly better than Kondrak’s met-
ric for each pair of ontologies. For the ontology 101,
when compared to itself, all methods above produce
1
http://oaei.ontologymatching.org/
the values of Precision, Recall and F-measure to be
1.0. The value of Recall is quite important because it
lets us estimate the number of true positives which is
compared to the number of existing correspondences
in the reference alignment. In general, with the same
value of Recall, the measure which is better provides
higher Precision. Although Recall values of Leven-
shtein, Kondrak, Jaro-Winkler, Needleman-Wunsch
measures and ours are similar for ontology 301, our
measure gives better Precision values than those of
these measures. That means our approach is better
than existing methods. Since ontology 301 consists
of concepts which are slightly or completely modi-
fied from reference ontology, the number of obtained
true positive concepts are the same for string-based
metrics mentioned before. Thus, in this case Recall
measures have the same values in all methods. Be-
cause ontology 204 only contains concepts modified
from the reference one by adding underscores, abbre-
viations and so on, the measures achieve the rather
high results of F-measure. Ontology 304 has simi-
lar vocabularies to the ontology 101, so Precision and
Recall values which are achieved for this pair of on-
tologies are also good. Jaro-Winkler measure is also
known as a good approach because its average Re-
call value is slightly higher than others. However its
average Precision is significantly lower than others,
for example: 0.773 compared to 0.930, 0.786, 0.899
and 0.957. Therefore, the number of obtained false
positive concepts of Jaro-Winkler is higher than other
measures. This phenomenon occurs in the same man-
ner in the pairs of ontologies 302 and 303.
Besides the above evaluation, our measure is also
more rational in several cases. For example, given
two strings c
1
=‘glass’ and c
2
=‘grass’. There is only
one edit transforming c
1
into c
2
: the substitution of
‘l’ with ‘r’. Therefore, the Levenshtein distance be-
tween two strings ‘glass’ and ‘grass’ is 1. Apply-
ing Eq. (11) and Eq. (22), the similarity between two
strings ‘glass’ and ‘grass’ is 0.8 while the similar-
ity degree of our measure yields 0.5. In fact, the
two strings ‘glass’ and ‘grass’ describe different ob-
jects. While the Levenshtein measure returns the
height similarity score value (0.8), the result 0.5 of
our measure is quite reasonable. In another exam-
ple, if n ≥ 2 then two strings Rep and Rap have no
n-grams in common. In this case, applying Dice’s
measure to these strings brings the dissimilarity. Ad-
ditionally, the family of Dice’s methods has a charac-
teristic which relies on the set of samples but not on
their positions. Because the sets of bigrams of two
strings Label and Belab including {la, ab, be, el} are
the same, the similarity value of these strings equal to
1, which seems inappropriate. In short, our approach
ApplyingInformation-theoreticandEditDistanceApproachestoFlexiblyMeasureLexicalSimilarity
509
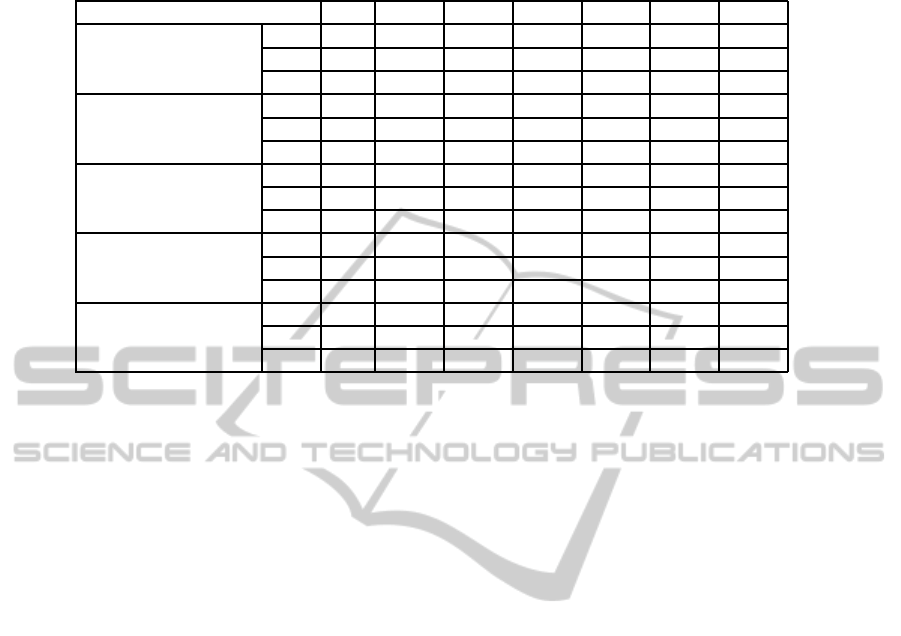
Table 1: Average Precision, Recall and F-measure values of different methods for six pairs of ontologies with thresholds
changed (Pre.=Precision, Rec.=Recall, F.=F-measure).
Measures 101 204 301 302 303 304 Avg.
Levenshtein
Pre. 1.0 0.982 0.835 0.929 0.880 0.955 0.930
Rec. 1.0 0.889 0.591 0.435 0.784 0.930 0.771
F. 1.0 0.933 0.692 0.592 0.829 0.942 0.832
Jaro-Winkler
Pre. 1.0 0.969 0.604 0.595 0.563 0.906 0.773
Rec. 1.0 0.956 0.591 0.469 0.833 0.933 0.797
F. 1.0 0.963 0.598 0.524 0.672 0.919 0.779
Needleman-Wunsch
Pre. 1.0 0.933 0.606 0.659 0.618 0.899 0.786
Rec. 1.0 0.909 0.591 0.459 0.778 0.930 0.778
F. 1.0 0.921 0.598 0.541 0.688 0.914 0.777
Kondrak
Pre. 1.0 0.967 0.797 0.871 0.810 0.951 0.899
Rec. 1.0 0.774 0.591 0.435 0.772 0.933 0.751
F. 1.0 0.860 0.679 0.580 0.790 0.942 0.809
Our measure
Pre. 1.0 0.989 0.888 0.949 0.952 0.965 0.957
Rec. 1.0 0.842 0.591 0.435 0.778 0.926 0.762
F. 1.0 0.910 0.710 0.596 0.856 0.945 0.836
overcomes the limits of these cases.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, we propose a new lexical-based ap-
proach, which considered the similarity of sequences
by combining features-based and element-based mea-
sures. This approach is motivated by Tversky’s and
Levenshtein’s measures; however, it is completely
different from original lexical methods previously
presented. The main idea of our approach is that the
similarity value of two given concepts depends not
only on the contents but also on the editing opera-
tions of these concepts in strings. For Levenshtein’s
measure, it focus on the number of editing opera-
tions in order to change one string into another string;
whereas, the characteristic of the Tversky’s model
contains the more common features and the less dif-
ferent features with an increasing in similarity be-
tween objects. For this reason, the combination of
the two above models reduces the limitations of other
methods. The experimentalvalidation of the proposed
metric has been conducted through six pairs of on-
tologies in OAEI benchmark 2008, and compared to
four of the common similarity metrics including Jaro-
Winkler, Needleman-Wunsch, Kondrak and Leven-
shtein metrics. The results show that our proposed
sequence similarity metric provides good values com-
pared to other existing metrics. Moreover, our metric
can be considered as flexible and generally lexical ap-
proach. In particular, adjusting the parameters α and
β produces the popular measures making convenient
experiments. It can also be implemented in many do-
mains in which strings are short as labels of concepts
in ontologies, proteins and so on.
In this work, strings are considered as a set of
characters. However, they can be extended to the set
of tokens in which the similarity between chunks in
plagiarism detection is calculated. In the future work,
our string-based similarity metric might also be com-
bined with relations between entities in ontologies us-
ing Wordnet dictionary to improve the semantic simi-
larity of pairs of these entities.
REFERENCES
Algergawy, A., Schallehn, E., and Saake, G. (2008). A
sequence-based ontology matching approach. In
The 10th International Conference on Information
Integration and Web-based Applications & Services,
pages 131–136. ACM.
Batet, M., S´anchez, D., and Valls, A. (2011). An ontology-
based measure to compute semantic similarity in
biomedicine. Biomedical Informatics, 44(1):118–125.
Dice, L. R. (1945). Measures of the amount of ecologic
association between species. Ecology, 26(3):297–302.
Euzenat, J. and Shvaiko, P. (2013). Ontology Matching.
Springer, 2nd edition.
Hamming, R. W. (1950). Error detecting and error cor-
recting codes. The Bell System Technical Journal,
29(2):147–160.
Ichise, R. (2008). Machine learning approach for ontology
mapping using multiple concept similarity measures.
In The 7th IEEE/ACIS International Conference on
Computer and Information Science, pages 340–346.
IEEE.
Jaccard, P. (1912). The distribution of the flora in the alpine
zone. The New Phytologist, 11(2):37–50.
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
510

Jaro, M. A. (1989). Advances in record-linkage method-
ology as applied to matching the 1985 census of
tampa, florida. The American Statistical Association,
84(406):414–420.
Kondrak, G. (2005). N-gram similarity and distance. In The
12th International Conference on String Processing
and Information Retrieval, pages 115–126. Springer.
Levenshtein, V. I. (1966). Binary codes capable of correct-
ing deletions, insertions, and reversals. Soviet Physics
Doklady, 10:707–710.
Lin, D. (1998). An information-theoretic definition of sim-
ilarity. In The 15th International Conference on Ma-
chine Learning, pages 296–304. Morgan Kaufmann.
Maedche, A. and Staab, S. (2002). Measuring similar-
ity between ontologies. In The 13th International
Conference on Knowledge Engineering and Knowl-
edge Management: Ontologies and the Semantic Web,
pages 251–263. Springer-Verlag.
Needleman, S. B. and Wunsch, C. D. (1970). A general
method applicable to the search for similarities in the
amino acid sequence of two proteins. Molecular Biol-
ogy, 48:443–453.
Nguyen, T. T. A. and Conrad, S. (2013). Combination
of lexical and structure-based similarity measures to
match ontologies automatically. In Knowledge Dis-
covery, Knowledge Engineering and Knowledge Man-
agement, volume 415, pages 101–112. Springer.
Pirr´o, G. and Euzenat, J. (2010). A feature and informa-
tion theoretic framework for semantic similarity and
relatedness. In The 9th International Semantic Web
Conference on The Semantic Web, pages 615–630.
Springer-Verlag.
Pirr´o, G. and Seco, N. (2008). Design, implementation and
evaluation of a new semantic similarity metric com-
bining features and intrinsic information content. In
On the Move to Meaningful Internet Systems: OTM
2008, pages 1271–1288. Springer.
S´anchez, D., Batet, M., Isern, D., and Valls, A. (2012).
Ontology-based semantic similarity: A new feature-
based approach. Expert Systems with Applications,
39(9):7718–7728.
Tversky, A. (1997). Features of similarity. In Psychological
Review, volume 84, pages 327–352.
Wang, X., Ding, Y., and Zhao, Y. (2006). Similarity
measurement about ontology-based semantic web ser-
vices. In The Workshop on Semantics for Web Ser-
vices.
Winkler, W. E. (1990). String comparator metrics and en-
hanced decision rules in the fellegi-sunter model of
record linkage. In The Section on Survey Research,
pages 354–359.
ApplyingInformation-theoreticandEditDistanceApproachestoFlexiblyMeasureLexicalSimilarity
511
