A Computational Algorithm for Dynamic Regrasping Using

Non-dexterous Robotic End-effectors

Avishai Sintov

∗

and Amir Shapiro

Department of Mechanical Engineering, Ben-Gurion University of the Negev, Beer-Sheva, Israel

1 STAGE OF THE RESEARCH

The presented research addresses the problem of re-

grasping an object. That is, to switch between grasp

conﬁgurations according to designated tasks to be

done. The state of the art in regrasping methods is

mostly quasi-static motions which requires high dex-

terous end-effectors. This research intends to ap-

proach the regrasping problem with dynamic ma-

nipulations. That is, utilize the dynamics of the

robotic arm to perform the regrasping operation while

grasping the object with a simple non-dexterous end-

effector.

As will be discussed further, in this research we

intend to perform the dynamic regrasping with two

strategies, one is the in-hand spinning and the other

is the mid-air ﬂipping. Currently, an algorithm for

motion planning of the in-hand spinning strategy was

developed. While approaching the problem and its

constraints, a method for dynamic motion planning

was needed. We surveyed methods which could

enable planning under kinematic and dynamic con-

straints and incorporate rendevouze planning of two

systems (arm and manipulated object). First, the

RRT (LaValle and Kuffner, 1999) planning method

was examined. However, the RRT method has dis-

advantage in dynamic planning with time constraint.

Therefore, we have modiﬁed the RRT and presented

the Time-Based RRT method (Sintov and Shapiro,

2014b) which could plan a dynamic motion with a

time constraint and use it for rendevouze planning.

However, this method was not fully compatible for

our needs, and we started developing our own dy-

namic planning algorithm.

The Semi-Stochastic Kinodynamic Planning

(SKIP) algorithm was developed. It was originally

developed for the regrasping problem, but is given as

a generic planning algorithm for any fully actuated

dynamic system. A journal paper of the full algo-

rithm was recently submitted (Sintov and Shapiro,

∗

The work presented in this paper is Avishai Sintov’s

PhD research under the supervision of Dr. Amir Shapiro.

2014a). The SKIP algorithm is a computational

algorithm, partially stochastic, for ﬁnding a feasible

trajectory for a dynamic system to move from an

initial state to a goal state under the kinematic and

dynamic constraints of the problem. It is proven to

ﬁnd a solution if such exists under a minimal known

probability.

The research is currently in an experimental

phase. A planar 3R robotic arm was built and posi-

tioned over an inclined hockey table. A set of mo-

tion capture cameras provides feedback of the ma-

nipulated objects state (position and orientation) at

all times. The servo motors also provide angle and

angular velocity feedback. These feedbacks with

the known Computed-Torque control scheme enables

motion of the arm to perform a desired regrasping mo-

tion according to the output of the SKIP algorithm.

Moreover, a model identiﬁcation computation method

and an adaptive computed torque control was imple-

mented to estimate unknown system parameters. The

main objective of the experiments is to validate the

performance of our dynamic planning algorithm and

the regrasping method.

The next stages of the research is the extension

of the algorithm for performing mid-air ﬂipping and

ﬁnally providing a general computation algorithm

givenanobject’s geometry and the desired ﬁnal grasp.

That is, the algorithm will independently choose the

desired regrasping strategy given a particular object.

For example, for a long cylinder the in-hand spinning

motion is not practical and mid-air ﬂipping should be

able to complete the motion.

2 OUTLINE OF OBJECTIVES

Dynamic regrasping is a new notion in robotics re-

search. The robot will initially spin the grasped ob-

ject into mid-air, then capture the object back at a new

grasp conﬁguration. This challenge will require sev-

eral key components:

• A consideration of the robot’s full dynamics in or-

Sintov A. and Shapiro A..

A Computational Algorithm for Dynamic Regrasping Using Non-dexterous Robotic End-effectors.

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

der to impose a desired release trajectory of the

free ﬂying object.

• A consideration of the ﬁngers’ opening process

to ensure release the object with a desired initial

spin.

• A visual servo system that will measure the free-

ﬂying object trajectory.

• Synthesis of a dynamic capturing trajectory for

the robot arm and its multi-ﬁnger hand.

• A consideration of the ﬁngers’ closing process in

order to achieve object re-capturing.

The project will evaluate two qualitatively distinct

dynamic regrasping strategies. The ﬁrst strategy is

termed in-hand spinning. The robot will release the

object into mid-air with an initial spin while opening

the ﬁngers into a partial cage formation. The robot

arm will then move the caging ﬁngers in tandem with

the ﬂying object, but without disturbing the object.

When the spinning object will reach a new desired

orientation relative to the hand’s mechanism, the ﬁn-

gers will capture the object by closing the cage around

the ﬂying object. The second strategy is termed mid-

air ﬂipping. Much like pancake or pizza ﬂipping, the

robot arm will initially spin the object high above the

robot arm mechanism. This will give the visual servo-

ing system and the robot arm ample time to measure

the object’s precise trajectory under the inﬂuence of

gravity. Based on this information, the arm will sub-

sequently move with open ﬁngers in order to capture

the ﬂying object at a pre-designated rendezvous loca-

tion in space. The research will evaluate the relative

merits of in-hand spinning and mid-air ﬂipping, with

the aim of identifying which type of objects are most

suitable for each strategy.

The research will additionally work out practi-

cal implementation procedures for the two regrasping

strategies. One promising procedure will start with

a selection of the robot arm release trajectory (posi-

tion and velocity), based on optimization criteria such

as total travel time, motors effort, trajectory smooth-

ness, and obstacle avoidance. The procedure will then

formulate a tracking control law based on classical in-

verse dynamics. The control law will subsequently be

modiﬁed to include corrective terms that compensate

for small modeling errors of the robot’s dynamics as

well as the small ﬁnger placement errors along the

object’s surface. A similar tracking control law will

be synthesized for the re-capturing trajectory. Finally,

the work will investigate how to robustify the regrasp-

ing procedure against small variations in the grasped

object parameters (for instance, its shape and mass

properties), in order to obtain a practically viable sys-

tem.

3 RESEARCH PROBLEM

3.1 Given System

Let Q ⊆ R

and U ⊆ R

be the conﬁguration space

and the set of all possible torque inputs, respectively

of a fully-actuated n-R robotic arm. The robotic arm

is equipped with a simple non-dexterous jaw-gripper

end-effector. Link i of the robot is with length L

. We

locate the world reference frame O at the base of the

manipulator. The conﬁguration space of the manipu-

lator Q ⊆ R

is deﬁned to be the set of all conﬁgura-

tions of the joint angles. The dynamic motion equa-

tions of the manipulatorin the conﬁguration space can

be written as

M(φ)

φ +C(φ,

φ)

φ+ G(φ)+ Γ = u (1)

where φ(t) = (ϕ

(t) ·· · ϕ

(t))

∈ Q is the conﬁgura-

tion of the arm at time t, M is the n× n inertia matrix,

C the n× n matrix of centrifugal and coriolis acceler-

ation terms, G is the n × 1 vector of gravitational ef-

fects, Γ is the n × 1 vector of joints frictional torques

and u(t) ∈ U is a vector of control input torques to

the joints.

Let T ⊆ R

×S

be the task space of the manip-

ulators end-effector where m

= 2, m

= 1 in the pla-

nar case (d = 2) and m

= 3, m

= 3 in the spatial case

(d = 3). We denote p

(t) ∈ T to be the task of the

end-effector at time t, that is, its position and orienta-

tion with respect to reference frame O. Moreover, we

deﬁne x

(t) = (p

(t)

)

∈ T × R

the state of the end-effector in cartesian coordinates.

We set a reference frame X

at the center of the end-

effector.

Given object B with mass m. We denote the

conﬁguration of the object in the task space of the

end-effector at time t by p

obj

(t). And therefore, its

state is given by x

obj

(t) = (p

obj

(t)

obj

(t)

)

∈ T ×

. Further, we deﬁne the relative state between

the end-effector and object.

Deﬁnition 1. The relative state between the end-

effector and object is deﬁned to be

x(t) =



obj

(t)}

(t) −

obj

(t)



(2)

where

obj

(t)}

= R

obj

(t)) · p

obj

(t) − d

obj

(t) (3)

is the task of the object with respect to X

, R

obj

∈

SO(d) : T → T and d

obj

(t) are the rotation map and

relative position, respectively, from reference frame

obj

to reference frame X

AComputationalAlgorithmforDynamicRegraspingUsingNon-dexterousRoboticEnd-effectors

The relative state expresses the relative position and

velocity between the end-effector and object. At time

t = 0, the end-effector and object are located at p

and

at rest, that is, x

(0) = x

obj

(0) = [p

. Therefore,

their initial relative state is

x(0) = 0. At that time, the

object is grasped by the end-effector such that the ob-

jects reference frame X

obj

overlaps the end-effectors

reference frame X

. That is, we deﬁne the initial ori-

entation and translation between corresponding refer-

ence frames to be zero (Figure 1a) with no relative

velocity as well.

3.2 Manipulation Goal

The regrasping problem is deﬁned as follows. Given

the initial relative state

x(0) and a desired relative

state goal

x(t

) = ζ, compute the control input se-

quence u(t) ∈ U, t ∈ [0, t

] to form an optimal manip-

ulation of the robotic arm such that the relative goal

is reached at some ﬁnite time t

∈ [0, ∞). An opti-

mal manipulation is the one forming a feasible trajec-

tory of the arm φ(t) ∈ Q such that the relative state

goal is reached while minimizing a given cost func-

tion H(φ(t)).

Generally speaking, the robotic arm will perform

some kind of manipulation to grant the object an ini-

tial velocity at release time t

and catch it again at

some time t

with relative state ζ. The primary goal of

this manipulation is to perform a set of motions such

that at the ﬁnal grasp the object will have a relative

state ζ = (ζ

)

where ζ

∈ T and ζ

∈ R

We can divide this goal to two fundamental con-

straints which must be achieved. The ﬁrst constraint

is demanded by the essence of the regrasping prob-

lem, i.e., to achieve a new desired grasp conﬁgura-

tion. This constraint states that the end-effector must

ﬁnally grasp the object with the same relative posi-

tion and orientation as in t = 0 but with an additional

desired offset ζ

. A planar example for this is illus-

trated in Figure 1b. Here ζ

= (ζ

)

where ζ

and ζ

are the translation components between coor-

dinate frames X

, X

obj

and ζ

is the relative orienta-

tion angle between the two. It should be noted that ζ

cannot be unequal to zero in a symmetric end-effector

but it is parameterized to preserve the generality of

the formulation. The second constraint is required for

proper manipulation. In order to obtain a soft inter-

ception and catch of the object at time t

, the end-

effector and the object must have equal velocities, that

is,

) =

obj

). In other words, we constrain ζ

to be

0 . (4)

In general, the ﬁnal goal of the regrasping manipula-

tion would be achieved if at some time t

∈ [0, ∞) the

following condition is met:

ρ(

x(t

) − ζ) ≈ 0 (5)

where ρ(·) is some metric criterion to be deﬁned.

The condition will be met if the metric distance is

close enough to zero, that is, the distance is within

a tolerance boundary to be deﬁned. Once condition

(5) is met (at time t

), the end-effector will regrasp

(jaws closure) the object at the desired relative state.

However,the end-effectorand the grasped object have

relative velocity with respect to coordinate frame O.

Therefore, after time t

where the object should be

ﬁrmly grasped by the end-effector, the manipulator

will gradually decelerate to zero velocity at ﬁnal time

3.3 Constraints

The above desired manipulation should be done under

the following constraints:

1. Based on actuators limitations, the allowed subset

of control input torques is given by U

⊂ U.

2. The conﬁguration of the arm is constrained to be

in Q

free

⊆ Q through the whole motion. Meaning,

the arms joints are limited within a certain range

due to mechanical and physical bounds.

3. Let V ⊂ R

denote the set of all possible veloci-

ties of the arms joints. The allowed joints veloci-

ties is deﬁned by the abilities of the actuators and

is given by V

⊆ V .

4. At time of release t

, to enable the object to se-

curely leavethe end-effector,the orientation of the

end-effector must be parallel to its velocity vector.

That is,

i = 0 . (6)

where r

∈ R

is the vector collinear to the last

link ﬁxed with the end-effector.

4 STATE OF THE ART

This paper deals with the regrasping problem in a

dynamic manipulation approach. Let us ﬁrst de-

scribe the two regrasping approaches taken by indus-

trial practitioners. The ﬁrst approach is the pick and

place method which designates a special work area

near each robot arm, where the grasped workpiece

can be dropped in a controlled manner, then picked

up again at a new grasp conﬁguration (Tournassoud

et al., 1987; Lozano-Pérez et al., 1987; Xue et al.,

2008). Alternatively, some high-end industrial practi-

tioners resort to ¸Sunthreading

T the regrasping task by

IJCCI2014-DoctoralConsortium

obj

, y

obj

, x

obj

, X

obj

(a) (b)

Figure 1: Initial and goal grasp conﬁgurations of the object by the end-effector: (a) both coordinate frames overlap in initial

grasp and (b) in the ﬁnal grasp the relative position and orientation between the coordinate frames are deﬁned by ζ

placing several (hugely expensive) robot arms along a

long production or assembly line, each picking a mov-

ing workpiece at a new grasp conﬁguration (Kim and

Park, 1995; Levitin et al., 2006). While both regrasp-

ing methods work nicely in practice, they consume

valuable production time, occupy a substantial work

area, and are highly expensive when multiple robot

arms are being used.

In the robotics literature, there are three known

approaches for regrasping (without picking and plac-

ing); First, the use of the end-effectors degrees of

freedom to move between contact points while main-

taining a force-closure grasp during the entire pro-

cess (Corves et al., 2011; de Paula Caurin and Feli-

cio, 2006; Roa and Suarez, 2009; Sudsang and Phoka,

2003; Vinayavekhin et al., 2011; Stuheli et al., 2013).

This approach is also called quasi-static ﬁnger gaiting

in the robotics literature. However, quasi-static ﬁn-

ger gaiting is quite wasteful, as it requires sufﬁciently

many degrees of freedom (requiring highly redun-

dant ﬁnger linkages) to manipulate the grasped object

between two grasp conﬁgurations while maintaining

force closure grasps. Most of the ﬁnger gaiting al-

gorithms use at least another extra ﬁnger that can be

lifted at each step (Grosch et al., 2008; Hasegawa

et al., 2003; Phoka and Sudsang, 2009; Rapela et al.,

2002). Such motion results in a slow quasi-static

manipulation, maintaining a state of constant contact

with the object. This has analogy to gait, where pro-

ceeding is done only with one leg lifted at a time

(when dynamic forces are not taken into considera-

tion) so that the other legs can maintain balance. Such

process can take valuable amount of time and there-

fore can be an impractical method. It has been re-

cently suggested that a dual arm robot may be more

suitable for object regrasping operations (Balaguer

and Carpin, 2012; Harada et al., 2012). While dual

arms is a promising approach, it has two signiﬁcant

drawbacks. First, regrasping an object with two co-

operating arms require highly dexterous manipulation

capabilities from both arms. Second, a dual-arm sys-

tem is costly and occupies a fairly large work volume.

The second approach is sliding the ﬁngertips on

the objects surface without losing contact to repo-

sition them at new contact points (Chen and Zribi,

2000; Cole et al., 1992). This approach has not been

widely researched and has low feasibility as it jeop-

ardizes the integrity of the object. Moreover, the ap-

proach needs also sufﬁciently enough degrees of free-

dom to develop trajectories on the objects surface.

The third approach is much faster and efﬁcient,

however more complex, as it uses dynamical manipu-

lations to switch between grasp conﬁgurations. In dy-

namic manipulation, the robotŠs motion is quick and

there is no constant contact state. The end-effector

lose contact (fully or partly) with the object after re-

leasing it in the air and regains contact by catching

it at the ﬁnal contact points. Such a method has

advantages in fast operation. However, most work

done in this ﬁeld use a multi-ﬁngered highly dexter-

ous hand for performing regrasping. Furukawa et al.

(Furukawa et al., 2006) proposed a regrasping strat-

egy based on visual feedback of the manipulated ob-

ject, this with a multi-ﬁngered hand. The work of

Tahara (Tahara et al., 2012) introduced a regrasping

method using a 3-ﬁnger hand with no external sens-

ing for feedback.

There is related work to dynamic regrasping in the

ﬁeld of dynamic manipulations (Senoo et al., 2008;

Srinivasa et al., 2005). Dynamic manipulation of

AComputationalAlgorithmforDynamicRegraspingUsingNon-dexterousRoboticEnd-effectors

an object enables the change of its position and ori-

entation by tossing, pushing or hitting it. Lynch et

al. (Lynch, 1997; Lynch et al., 1998) developed a

low degree of freedom robot to perform complex ma-

nipulations using rolling, sliding and free-ﬂight, this

with no grasping (non-prehensile manipulation). In

(Tabata and Aiyama, 2001) a one degree of freedom

manipulator was used to toss an object to a goal po-

sition. The work by (Higashimori et al., 2009) was

done to mimic the manipulation done with a pizza

peel. The research states that the pizza peel is con-

trolled with only two degrees of freedom and uti-

lizes vision control. Much work has also been done

in pushing manipulations where the object is pushed

on a desired trajectory to re-position or re-orient it

(Lynch, 1992; Bernheisel and Lynch, 2006; Kopicki

et al., 2010). Moreover, some performed manipu-

lation of the grasped objects by dynamic manipula-

tions between ﬁngertips (Garcia-Rodriguez and Diaz-

Rodriguez, 2011; Yashima and Yamaguchi, 2002).

Another research area regarding the regrasping is

rendezvous planning of two dynamic systems where

only one is controlled. That is, matching the states

of two dynamic systems within a ﬁnite time. Many

solutions to this problem were presented; The pro-

portional navigation algorithm is a commonly used

method to account for a moving object such as a UAV

or a missile (Erer and Merttopçuoglu, 2012; Mehran-

dezh et al., 2000). The advantage of the algorithm

is in its simplicity and is shown to be complete as it

will intercept the object in ﬁnite time. Many other

rendezvous algorithms for optimal trajectories were

presented to ﬁnd the best trajectory in a dynamic en-

vironment (Michael et al., 2013; Rybus and Sew-

eryn, 2013). Another method for dynamic planning

is the Rapidly-exploring Random Tree (RRT) which

is a probabilistic method for trajectory planning in a

complex environment taking the dynamics of the sys-

tem into account (Kothari and Postlethwaite, 2013;

Kuwata et al., ; LaValle and Kuffner, 1999; Luders

et al., 2010; Shkolnik et al., 2009). The authors have

tried to use the RRT method for rendezvous planning

and further use it for dynamic regrasping (Sintov and

Shapiro, 2014b). However, this method has many dif-

ﬁculties working in real-time due to high complexity

and therefore not feasible for our objective.

5 METHODOLOGY

The approach method for solving the above problem

can be divided into three parts; First, we parameter-

ize the motion of the arm in its two phases, release

phase and free-ﬂight phase. That is, the motion of the

arm is described as a vector σ. The next part is the

formulation of the problems constraints in terms of

time t and the parameter vector σ. The new formula-

tion of the constraints deﬁnes a time-varyingsubspace

in σ-space. A feasible motion of the arm under the

constraints is a solution vector σ

∗

which lies within

the time-varying subspace for the whole motion. The

problem of ﬁnding such a feasible solution is termed

as the Time-Varying Constraint (TVC) problem. In

the third part of the solution, a semi-stochastic algo-

rithm was developed to solve the TVC problem and

ﬁnd a feasible and optimal solution. An optimal so-

lution is the one which minimizes a pre-deﬁned cost

function H(σ). The followingsubsections give a short

overview of the solution parts.

5.1 Motion Parameterization

As mentioned, the regrasping motion is composed of

two main phases: the release phase and the free-ﬂight

phase. In this section we parameterize this motion

to the parameters which are the DOF of the trajec-

tory. First we parameterize the motion in the free-

ﬂight phase. Then, based on the initial task and ve-

locity (release state) at the beginning of the free-ﬂight

phase, we parameterize the release phase as a polyno-

mial trajectory from the robots initial state to the re-

lease state. That is, we parameterize a polynomial tra-

jectory which could provide the initial velocity at the

release position demanded for the free-ﬂight phase.

In this section we present the structure of σ

and

. Then, we present the formulation of the problems

constraints in terms of time and σ.

5.1.1 Free-ﬂight Phase

The free-ﬂight motion of the object depends on its re-

lease position and release velocity. That is, granting

the object an initial velocity

obj

) from initial po-

sition and orientation (task) p

obj

) deﬁnes its trajec-

tory with no control ability. Once the object is re-

leased, its free-ﬂight trajectory is a projectile motion

solely under the inﬂuence of gravity. Therefore, the

deﬁnition of motion in this phase includes the initial

task and velocity at time t

Moreover, the estimated time for the end-effector

and the object to reach the desired relative state, e.g.,

satisfaction of condition (5), is deﬁned by the gains

of the Computed-Torque controller to be used. There-

fore, the proportional gains of the controller deﬁnes

the time of interception t

with the object.

With the understanding of the parameters which

deﬁne the free-ﬂight phase, we deﬁne the parameters

vector σ

. The form of the parameters vector σ

∈

IJCCI2014-DoctoralConsortium

in the free-ﬂight phase is deﬁned as follows:



··· k



. (7)

where p

= p

obj

) and

obj

) are the task

and velocity of the end-effector which would be

granted to the object at time t

, and d

= 2m

+ 2m

n. Vector σ

is a parameterization of the free-ﬂight

phase and its determination deﬁnes the approximated

trajectory and motion time of the arm.

5.1.2 Release Phase

The parameterization of the release phase presented

here is the one introduced by (Sintov and Shapiro,

2014a). In this phase we must provide a trajectory

from the robots initial state at time t = 0 to the de-

sired release state at time t

presented in the previ-

ous subsection. That is, given the robots initial task

(0) = p

at rest, we need a trajectory s(t) that will

satisfy the following boundary conditions:











s(0) = p

s(0) = 0

s(t

) = p

s(t

) =

(8)

First we deﬁne an optional candidate trajectory which

could complete the task.

Deﬁnition 2. A trajectory function s(t) ∈ T is a can-

didate trajectory if it is differentiable and satisﬁes

some h boundary constraints.

That is, in our motion planning problem, a tra-

jectory s(t) is a candidate trajectory if it satisﬁes the

h = 4m boundary constraints in (8) which impose the

initial and release states. The following deﬁnition de-

scribes a candidate trajectory function which is con-

strained by the problems boundary constraints and has

redundant DOF to optimize.

Deﬁnition 3. A candidate trajectory function s(t) =

(t, w) ∈ T , where w = [w

··· w

m·k

]

∈ R

m·k

and

has h boundary constraints, is redundant if m· k > h.

The four constraints in (8) impose the values for

, ..., w

and leave k−4 free parameters for the func-

tion. Moreover, the goal time t

can also be chosen

as a free parameter if no time constraint is imposed.

Therefore, the redundant parameters are denoted as

= [w

h+1

··· w

m·k

]

∈ R

, where d

= k − 4+1.

If the goal time t

is ﬁxed, it should not be included in

the parameter vector σ

A redundant trajectory function s(t) = f

(t, σ

) is

chosen as the desired trajectory from the initial state

to the goal state. The function imposes the bound-

ary constraints while providing a desired number of

free parameters for motion planning and optimiza-

tion. Such redundant trajectories could take, for ex-

ample, polynomial form or be a fourier series. In this

work we implement the use of a redundant polyno-

mial function due its simplicity.

5.1.3 Overall Parameterization

The release phase parameters vector σ

and the free

ﬂight parameters vector σ

can now be generalized to

one vector σ which is a parameterization of the whole

motion

σ =





∈ Ω (9)

where Ω ⊆ R

. The determination of σ will fully

deﬁne the nominal trajectory of the motion from ini-

tial rest position of the arm (t = 0), through release of

the object (t = t

) to ﬁnally regrasping it at the desired

relative state (t = t

). The strength of this parameteri-

zation is that a single vector deﬁnes a speciﬁc regrasp-

ing motion independent of time.

5.2 Constraints Formulation

In this part we formulate the constraints of the sys-

tems motion in terms of the free parameters of the

problem. We formulate conﬁguration space con-

straints which deﬁne Q

free

, other constraints in the

task space, and ﬁnally velocity and torque constraints

imposed by the limitations of the system. For exam-

ple, due to joint limitations, it is possible that not all

the conﬁguration space Q of the arm is accessible.

Therefore, we can formulate the free space Q

free

ex-

plicitly as a set of z

constraints Φ ∈ R

(φ(t)) = Φ

(t, σ) ≤ 0, ∀i = 1, ..., z

. (10)

The same could be done to the velocity, torque and

workspace constraints. The set of inequalities ac-

quired could be written as

(t, σ) ≤ 0, i = 1, ..., z (11)

where Ψ(t, σ) is a set of z functions which deﬁne the

systems constraints. Inequality (11) deﬁnes the fea-

sible region of the dynamic system in terms of time

and the desired trajectory parameters σ. That is, we

obtained a set of constraints which deﬁnes a time-

varying region in Ω. The next section presents the

time-varying constraint problem and the search algo-

rithm to ﬁnd an optimal trajectory satisfying the con-

straints.

5.3 Time-varying Constraint (TVC)

Problem

In the previous section we obtained a set of inequali-

ties depending on t and the parameters vector σ. Re-

AComputationalAlgorithmforDynamicRegraspingUsingNon-dexterousRoboticEnd-effectors

Ψ(t

, σ) = 0

Ψ(t

, σ) = 0

Ψ(t

, σ) = 0

Ψ(t

, σ) = 0

∗

Ω

Figure 2: The TVC problem where t

< t

call that the components in σ are independent of the

time. Therefore, we would like to ﬁnd an optimal vec-

tor σ

∗

∈ Ω that satisﬁes the constraints through the

regrasping motion and minimizes some cost function.

Such an optimal vector will sufﬁciently deﬁne the mo-

tion of the system under the kinodynamic constraints.

Let Σ ⊂ Ω be the allowed region for σ. We deﬁne the

notion of a feasible set.

Deﬁnition 4. A set Ω

⊂ Ω is a feasible set in t ∈

] if Ω

⊆ Σ and each σ ∈ Ω

satisﬁes inequality

(11) for all time t ∈ [t

We now deﬁne a feasible vector.

Deﬁnition 5. A vector of trajectory parameters σ ∈

is said to be feasible in t ∈ [t

] if σ ∈ Ω

The above two deﬁnitions conclude that a vector is

feasible if

σ =



σ ∈ Ω

|σ ∈ Σ, Ψ

(t, σ) ≤ 0, ∀t ∈ [t

(σ),t

(σ)]



(12)

for all i = 1, ..., z. Notice that the time interval is writ-

ten in general [t

(σ),t

(σ)] and is a function of σ. This

is due to the deﬁnition of the free parameters vector σ,

which could include parameters that deﬁne the oper-

ation time. Therefore, the choice of σ determines the

boundary time. We now face the problem of ﬁnding

the feasibility set Ω

⊆ Σ where for all vectors within

it, inequality (11) is maintained at all times. Formally,

the problem is as follows.

Problem 1. Given the set of constraints in (11) and

the set Σ, ﬁnd the feasibility set Ω

⊆ Σ.

Solving the above problem provides the feasible

set Ω

from which the optimal solution is to be cho-

sen. Hence, we deﬁne the following minimization

problem.

Problem 2. Find the vector σ

∗

∈ Ω

where Ω

⊆ Σ

such that

∗

= argmin

H(σ)

subject to σ

∗

∈ Ω

(13)

where H(σ) is some cost function to minimize.

Ψ(t

, σ) = 0

Ψ(t

, σ) = 0

, σ

)

, σ

)

(λt

+ (1 − λ)t

, σ

)

Figure 3: Vector σ satisfying Lemma 1.

In other words, the above general problem is ﬁnd-

ing an optimal vector σ

∗

that is feasible and mini-

mizes some cost function H(σ) to be determined. Fig-

ure 2 illustrates the two problems. The position and

volume of Ψ(t, σ) in Ω varies in time and therefore,

the solution of the problem is in a domain formed by

projecting the constraints for time t

to t

on space Ω.

The intersection formed by these projections, if one

exists, is the feasibility domain that the optimal solu-

tion σ

∗

should be chosen from.

A search algorithm is now desired to ﬁnd the set

Ω

of feasible vectors. The domain formed by the

set of constraints in inequality (11) is non-linear, non-

convex, and not continuous. Therefore, an analytical

solution of the reachable set is only possible in rare

and simple instances. We present a numerical search

algorithm to ﬁnd a set of vectors satisfying the above

constraints. Further, we can choose one vector from

the set that best minimizes the cost function. We be-

gin by presenting a simple deﬁnition for normalizing

the time interval.

Lemma 1. A vector σ is feasible in t ∈ [t

] if the

constraint Ψ

(λt

+(1− λ)t

, σ) ≤ 0 is satisﬁed for all

0 ≤ λ ≤ 1 and for all i = 1, ..., z.

Proof. For each time instant t ∈ [t

] there exists λ

such that t = λt

+(1− λ)t

and 0 ≤ λ ≤ 1. Therefore,

if a vector σ satisﬁes Ψ

(t, σ) ≤ 0 for all i = 1, ..., z and

≤ t ≤ t

, it must also satisfy Ψ

(λt

+(1− λ)t

, σ) ≤

0 for all i = 1, ..., z and 0 ≤ λ ≤ 1.

Lemma 1 is utilized as a criterion for determining

whether a vector σ is feasible. Numerically, for σ we

check the constraint for time t = λt

+ (1 − λ)t

with

λ = {0, ∆λ

, ∆λ

+ ∆λ

, ..., 1}. The value of the step

∆λ

will be further deﬁned. Figure 3 illustrates an

abstraction of the feasibility problem and the line in

time deﬁned by Lemma 1. Without loss of generality,

from this point we will address the problem with the

time frame [t

] = [0, t

The basis of the algorithm’s operation is selecting

a set of N random points within Σ and checking each

IJCCI2014-DoctoralConsortium

Algorithm 1: Feasibility_search(Σ, Ψ, P

max

, ε

Input: The allowed set Σ, set of constraints Ψ, the

probability P

max

, and tolerance ε

Output: Set of feasible points Ω

1: Calculate number of random points N such that the

probability to ﬁnd a solution is more than 1− P

max

2: Generate the set P = {σ

, ...,σ

} of N uniformly

distributed random points within Σ.

3: for i = 1 → N do

4: if ¬(Adaptive_Check(σ

, Ψ, ε

)) then

5: Remove σ

from P .

6: end if

7: end for

8: return Ω

= P = {σ

, ...,σ

} // M ≤ N

for its feasibility. The feasibility search algorithm is

presented as the Feasibility_Search(Σ, Ψ) function in

Algorithm 1. The algorithm’s input is the allowed set

Σ in Ω chosen by the user and the set of constraints

of equation (11). The ﬁrst step of the algorithm is to

determine the number of random points N such that

the probability to ﬁnd a solution is more than a user

deﬁned probability 1 − P

max

. The calculation of N

based on the choice of P

max

will be presented later

in the algorithm’s analysis. The next step is to sample

N random points P uniformly distributed in Σ. The

allowed region formed by Σ is a hyper-rectangle in

Ω and therefore we sample points in each axis of Ω

within the boundaries deﬁned by Σ. Such sampling

provides a Poisson distribution over the volume of Σ.

The next step is going over all the N points in P and

ﬁltering out those that are not feasible. The ﬁnal time

is determined for each point σ

checked. We check

if the constraints are satisﬁed for time t = λt

where

λ = {0, ∆λ

, ∆λ

+ ∆λ

, ..., 1}. Those that do not sat-

isfy the constraints are eliminated and the ﬁltered set

P with size M ≤ N is outputted.

Scanning the constraint Ψ(λt

, σ

) for λ =

{0, ∆λ, 2∆λ, ..., 1} where ∆λ is a constant value is

rather risky. The value of Ψ might ascend over 0

and descend below again within the discretized step

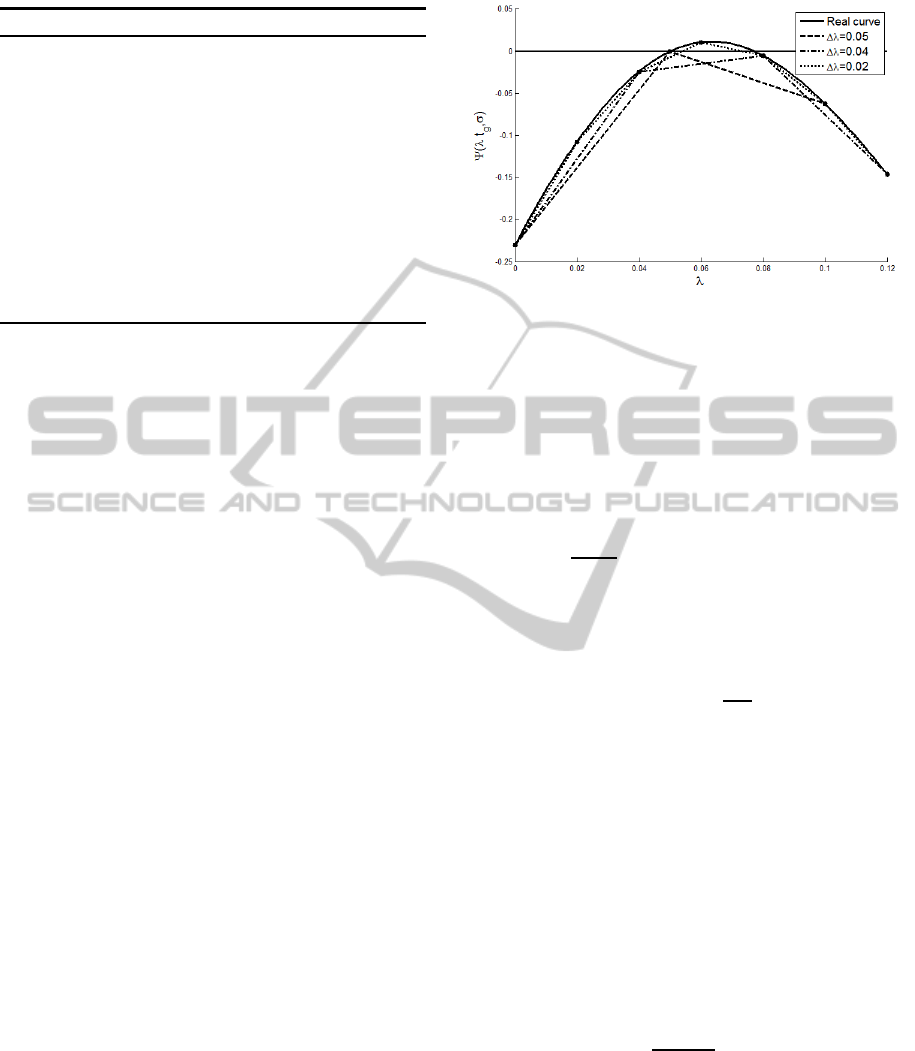
size. An example of such is shown in Figure 4 where

with step size above 0.03 failure of the constraints

might not be discovered. Moreover, too small step

sizes could be unnecessary and the price would in-

clude very high complexity. Therefore, we present a

simple adaptive step size algorithm to ﬁne tune the

time steps and diagnose or rule out such scenarios.

Deﬁnition 6. The constraint value of a feasible point

at time λt

is deﬁned to be

i,λ

= max



(λt

, σ

)



, (14)

where Ψ

is the j

component of the constraint vector

Ψ.

Figure 4: The maximum constraint value along time with

change of the step size ∆λ.

That is, the constraint value is the shortest dis-

tance from point σ

to the boundary of the closest con-

straint. Notice that we refer to a distance with a posi-

tive value, but the value of

i,λ

is maintained negative

for an indication that σ

is a feasible point. Assume

that the change rate of the constraint value with regard

to λ is bounded by

∆

i,λ

∆λ

≤ S

max

, ∀ 0 ≤ λ ≤ 1 . (15)

That is, the maximum slope of the constraint value

i,λ

is S

max

. Under this assumption we can say that

if at time λt

the constraints are satisﬁed,

i,λ

< 0,

then the minimum time for the constraint to reach 0 is

(λ+∆λ

min

where ∆λ

min

= −

i,λ

max

. Therefore, as we

get closer to a boundary of a constraint, we decrease

∆λ such that reaching above the zero line in that time

frame is not possible. Figure 5 illustrates the selec-

tion of ∆λ as it gets smaller when approaching the

zero line and larger when receding. However, in this

adaptive approach, even though

i,λ

passes the zero

line, the algorithm will never do so as it will continue

to decrease ∆λ. Therefore, we bound such that the

algorithm will stop checking the current σ

(and re-

move it) if

i,λ

< ε

< 0, where ε

is a value that will

be deﬁned further in the algorithm’s analysis. This

also serves as a safety distance, assuring the solution

is far enough from the constraints boundary. To cal-

culate S

max

we differentiate the constraint vector by

λ to acquire its slope

∂Ψ(λt

,σ)

∂λ

, where t

is the max-

imum possible goal time based on the allowed time

interval given in Σ. S

max

is the maximum slope of all

components over all time and can be computed by the

following maximization problem

max

= max

λ,σ, j

(λt

, σ)

subject to 0 ≤ λ ≤ 1

σ ∈ Σ

(16)

AComputationalAlgorithmforDynamicRegraspingUsingNon-dexterousRoboticEnd-effectors

Figure 5: Adaptive step size algorithm.

Ω

Figure 6: Two-dimensional example of Σ and Ω

in Ω.

where S

is the j

component of the constraints

derivative S(λt

, σ) =

∂Ψ(λt

,σ)

∂λ

. This could be

computed analytically using Kuhn-Tucker conditions

or numerically. The adaptive step size function

Adaptive_Check(σ

, Ψ) is presented in Algorithm 2.

Algorithm 2: Adaptive_Check(σ

, Ψ, ε

Input: σ

, the set of constraints Ψ and the tolerance ε

Output: Boolean: 1 if σ

is feasible, 0 if not feasible.

1: Set λ = 0.

2: Extract t

from the last component of σ

3: Calculate S

max

. // using optimization prob. in (16).

4: while ( λ ≤ 1 ) do

5: Calculate

i,λ

= max

{Ψ

(λt

, σ

)}.

6: if ¬(

i,λ

< ε

) then

7: Return 0.

8: else

9: Calculate ∆λ = −

i,λ

max

10: λ = λ + ∆λ.

11: end if

12: end while

13: Return 1.

The ﬁnal step of the algorithm is selecting the op-

timal solution among the set of feasible points Ω

{σ

, ..., σ

} found in Algorithm 1 and perform lo-

cal ﬁne-tuning optimization. Given the cost function

H(σ), the optimal solution σ

∗

is found according to

Algorithm 3. In this algorithm, ﬁrst a simple naive

search is performed on the feasibility set Ω

to ﬁnd a

feasible point σ

that best minimizes H(σ) (Line 1).

Next, we utilize a Gradient Descent (GD) method (?)

to reﬁne the solution and ﬁnd a local minimum in the

neighborhood of σ

. The GD method is an iterative

algorithm with an update law of the form

(i+1)

= σ

(i)

− γ∇H(σ

(i)

) (17)

for some small γ > 0 (Line 5). In each iteration a

check is done to avoid breaking the constraints. No-

tice that the Adaptive_Check function preventsthe so-

lution from approaching the constraint boundary with

distance less than ε

. The iterations are terminated

if the new point breaks the constraints or if the con-

vergence condition is satisﬁed (Line 10 of Algorithm

3). Figure 7 presents two examples of local reﬁne-

ment of the optimal solution; one was stopped by the

constraint while the other managed to reach the lo-

cal minimum. The convergence condition checks if

the norm of the current descent is smaller than a pre-

deﬁned tolerance ε

, that is, we have reached a local

minimum with ε

accuracy. The last point of the it-

eration is the optimal solution and is returned by the

algorithm.

Algorithm 3: Local_Optimization(Ω

, ε

Input: Feasible set Ω

= {σ

, ...,σ

} and tolerance

Output: Optimal solution σ

∗

1: k = argmin

H(σ

), i = 1, ..., M

2: Deﬁne σ

(0)

= σ

3: i = 0.

4: repeat

5: σ

(i+1)

= σ

(i)

− γ∇H(σ

(i)

6: if ¬(Adaptive_Check(σ

(i+1)

)) then

7: Return σ

(i)

8: end if

9: i = i+ 1.

10: until



∇H(σ

(i)

)



< ε

11: σ

∗

= σ

(i)

12: Return σ

∗

Ω

∗

Ω

∗

Figure 7: Two examples of the optimal solution reﬁnement;

one (left) descends to the local minimum and one (right) is

stopped by the constraint boundary.

IJCCI2014-DoctoralConsortium

Statistical analysis which was performed have

proven that it is possible to determine the minimal

probability to ﬁnd a solution if such exists. a solution

if one exists.

6 EXPECTED OUTCOME

This work addresses the problem of reducing the

number of end-effectors needed in the production for

grasping a number of parts and performing several

tasks on them. Dynamic regrasping approach will

be addressed for transition between required grasps

to perform designated tasks. The idea for the re-

grasping operation is to perform it with a simple non-

dexterous end-effector and with the dynamics of the

robotic arm.

As presented, currently the algorithm has the capa-

bilities for computation of an in-hand spinning mo-

tion for regrasping. The next phase of the research

is extension of the planning algorithm to compute the

motion of the mid-air ﬂipping. These two methods

should provide most of the dynamic regrasping needs.

The ﬁnal outcome will be an overall algorithm for

computation of a regrasping motion given an object’s

geometry and the goal relative state. That is, the algo-

rithm will choose the best regrasping strategy accord-

ing to the objects geometry and desired ﬁnal grasp.

Looking in a wider application for the regrasping

motion. The ﬁeld of robotic grasping is very wide

and serve many civil, industrial and military areas.

The regrasping operation is performed whenever the

grasp conﬁguration is not compatible to the future

task to be done. Many industrial and civilian ap-

plications demand change of the grasp conﬁguration

to achieve desired tasks. In many applications we

demand fast and efﬁcient performance of the tasks.

Moreover, we desire simple low cost arms to con-

duct the tasks. For example, in the industrial world

of today, fast and efﬁcient production is highly im-

portant. However, achieving so must be accompanied

with low costs to ensure a reasonable ﬁnal product

price. Our proposed research will impact the number

of robotic arms and end-effectors used in production

lines. Currently, each end-effector is specially de-

signed for grasping a speciﬁc object and performing a

speciﬁc task. They are used for assembly or material

handling. The more end-effector needed, the more

robotic arms, tool changers, and services are needed.

Moreover, they demand more operational space in the

plant. Using the same robotic arm and end-effector

for multiple tasks will drastically reduce the num-

ber of robotic arms needed and reduce the demand

for technical and engineering services. An additional

advantage would be in the production time. The dy-

namic regrasping algorithm would have great beneﬁt

in shortening the material handling time of transfer-

ring objects between end-effectors because the object

remains in the same end-effector.

REFERENCES

Balaguer, B. and Carpin, S. (2012). Bimanual regrasping

from unimanual machine learning. In Proceedings of

the IEEE International Conference on Robotics and

Automation (ICRA), pages 3264 –3270.

Bernheisel, J. and Lynch, K. (2006). Stable transport of as-

semblies by pushing. IEEE Transactions on Robotics,

22(4):740 –750.

Chen, J. and Zribi, M. (2000). Control of multiﬁngered

robot hands with rolling and sliding contacts. The In-

ternational Journal of Advanced Manufacturing Tech-

nology, 16:71–77.

Cole, A., Hsu, P., and Sastry, S. (1992). Dynamic control of

sliding by robot hands for regrasping. IEEE Transac-

tions on Robotics and Automation, 8(1):42 –52.

Corves, B., Mannheim, T., and Riedel, M. (2011). Re-

grasping: Improving capability for multi-arm-robot-

system by dynamic reconﬁguration. In Jeschke,

S., Liu, H., and Schilberg, D., editors, Intelligent

Robotics and Applications, volume 7101 of Lecture

Notes in Computer Science, pages 132–141. Springer

Berlin Heidelberg.

de Paula Caurin, G. A. and Felicio, L. C. (2006). Learning

based regrasping applied to an antropomorphic robot

hand. ABCM Symposium series in mechatronics.

Erer, K. S. and Merttopçuoglu, O. (2012). Indirect Impact-

Angle-Control Against Stationary Targets Using Bi-

ased Pure Proportional Navigation. Journal of Guid-

ance Control Dynamics, 35:700–704.

Furukawa, N., Namiki, A., Taku, S., and Ishikawa, M.

(2006). Dynamic regrasping using a high-speed mul-

tiﬁngered hand and a high-speed vision system. In

Proceedings of the IEEE International Conference on

Robotics and Automation (ICRA), pages 181 –187.

Garcia-Rodriguez, R. and Diaz-Rodriguez, G. (2011).

Grasping and dynamic manipulation by soft ﬁnger-

tips without object information. In Proceedings of

the 9th IEEE International Conference on Control and

Automation (ICCA), pages 766 –771.

Grosch, P., Suarez, R., Carloni, R., and Melchiorri, C.

(2008). Planning setpoints for contact force transi-

tions in regrasp tasks of 3d objects. In Proceedings

of the 17th IFAC World Congress, volume 17, pages

6776–6781, Seoul, Korea. IFAC International Federa-

tion of Automatic Control.

Harada, K., Foissotte, T., Tsuji, T., Nagata, K., Yamanobe,

N., Nakamura, A., and Kawai, Y. (2012). Pick and

place planning for dual-arm manipulators. In Pro-

ceedings of the IEEE International Conference on

Robotics and Automation (ICRA), pages 2281 –2286.

Hasegawa, Y., Higashiura, M., and Fukuda, T. (2003). Sim-

pliﬁed generation algorithm of regrasping motion -

AComputationalAlgorithmforDynamicRegraspingUsingNon-dexterousRoboticEnd-effectors

performance comparison online-searching approach

with ep-based approach. In Proceedings of the IEEE

International Conference on Robotics and Automation

(ICRA), volume 2, pages 1811 – 1816 vol.2.

Higashimori, M., Utsumi, K., Omoto, Y., and Kaneko, M.

(2009). Dynamic manipulation inspired by the han-

dling of a pizza peel. IEEE Transactions on Robotics,

25(4):829 –838.

Kim, H. and Park, S. (1995). A strong cutting plane al-

gorithm for the robotic assembly line balancing prob-

lem. International Journal of Production Research,

33(8):2311–2323.

Kopicki, M., Stolkin, R., Zurek, S., Morwald, T., and Wyatt,

J. (2010). Predicting workpiece motions under push-

ing manipulations using the principle of minimum en-

ergy. In Proceedings of the RSS workshop on Repre-

sentations for Object Grasping and Manipulation in

Single and Dual Arm Tasks. submitted.

Kothari, M. and Postlethwaite, I. (2013). A probabilisti-

cally robust path planning algorithm for uavs using

rapidly-exploring random trees. Journal of Intelligent

& Robotic Systems, 71(2):231–253.

Kuwata, Y., Teo, J., Member, S., Fiore, G., Member, S.,

Karaman, S., Member, S., Frazzoli, E., Member, S.,

How, J. P., and Member, S. Realtime motion planning

with applications to autonomous urban driving. IEEE

Transactions on Control Systems, page 2009.

LaValle, S. and Kuffner, J.J., J. (1999). Randomized kin-

odynamic planning. In Proceedings of the IEEE In-

ternational Conference on Robotics and Automation,

volume 1, pages 473–479.

Levitin, G., Rubinovitz, J., and Shnits, B. (2006). A genetic

algorithm for robotic assembly line balancing. Euro-

pean Journal of Operational Research, 168(3):811 –

825.

Lozano-Pérez, T., Jones, J. L., Mazer, E., O’Donnell, P. A.,

Grimson, W. E. L., Tournassoud, P., and Lanusse, A.

(1987). Handey: A robot system that recognizes,

plans, and manipulates. In IEEE International Confer-

ence on Robotics and Automation, pages 843=–849.

Luders, B., Karaman, S., Frazzoli, E., and How, J. (2010).

Bounds on tracking error using closed-loop rapidly-

exploring random trees. In American Control Confer-

ence (ACC), pages 5406–5412.

Lynch, K., Shiroma, N., Arai, H., and Tanie, K. (1998). The

roles of shape and motion in dynamic manipulation:

the butterﬂy example. In Proceedings of the IEEE In-

ternational Conference on Robotics and Automation,

volume 3, pages 1958 –1963 vol.3.

Lynch, K. M. (1992). The mechanics of ﬁne manipulation

by pushing. In Proceedings of the IEEE International

Conference on Robotics and Automation, pages 2269–

2276.

Lynch, K. M. (1997). Dynamic manipulation with a one

joint robot. In Proceedings of the IEEE International

Conference on Robotics and Automation, pages 356–

366.

Mehrandezh, M., Sela, N., Fenton, R., and Benhabib, B.

(2000). Robotic interception of moving objects using

an augmented ideal proportional navigation guidance

technique. IEEE Transactions on Systems, Man and

Cybernetics, 30(3):238–250.

Michael, J., Chudej, K., Gerdts, M., and Pannek, J. (2013).

Optimal rendezvous path planning to an uncontrolled

tumbling target.

Phoka, T. and Sudsang, A. (2009). Contact point clustering

approach for 5-ﬁngered regrasp planning. In Proceed-

ings of the IEEE/RSJ International Conference on In-

telligent Robots and Systems, pages 4174 –4179.

Rapela, D., Rembold, U., and Kuchen, B. (2002). Planning

of regrasping operations for a dextrous hand in assem-

bly tasks. Journal of Intelligent and Robotic Systems,

33:231–266.

Roa, M. A. and Suarez, R. (2009). Regrasp planning in the

grasp space using independent regions. In Proceed-

ings of the 2009 IEEE/RSJ international conference

on Intelligent robots and systems, IROS’09, pages

1823–1829, Piscataway, NJ, USA. IEEE Press.

Rybus, T. and Seweryn, K. (2013). Trajectory planning

and simulations of the manipulator mounted on a free-

ﬂoating satellite. In SÄ

Esiadek, J., editor, Aerospace

Robotics, pages 61–73. Springer.

Senoo, T., Namiki, A., and Ishikawa, M. (2008). High-

speed throwing motion based on kinetic chain ap-

proach. In IROS, pages 3206–3211.

Shkolnik, E., Walter, M., and Tedrake, R. (2009).

Reachability-guided sampling for planning under dif-

ferential constraints. In in In Proceedings of the

IEEE/RAS International Conference on Robotics and

Automation (ICRA).

Sintov, A. and Shapiro, A. (2014b). Time-based RRT al-

gorithm for rendezvous planning of two dynamic sys-

tems. In Proceedings of the IEEE International Con-

ference on Robotics and Automation.

Sintov, A. and Shapiro, A. (Submitted July 2014a).

Skip: Semi-stochastic kinodynamic planning algo-

rithm. The IEEE Transactions on Robotics.

Srinivasa, S., Erdmann, M., and Mason, M. (2005). Using

projected dynamics to plan dynamic contact manipu-

lation. In Proceedings of the IEEE/RSJ International

Conference on Intelligent Robots and Systems, pages

3618 – 3623.

Stuheli, M., Caurin, G., Pedro, L., and Siegwart, R. (2013).

Squeezed screw trajectories for smooth regrasping

movements of robot ﬁngers. Journal of the Brazil-

ian Society of Mechanical Sciences and Engineering,

35(2):83–92.

Sudsang, A. and Phoka, T. (2003). Regrasp planning for a 4-

ﬁngered hand manipulating a polygon. In Proceedings

of the IEEE International Conference on Robotics and

Automation, volume 2, pages 2671 – 2676 vol.2.

Tabata, T. and Aiyama, Y. (2001). Tossing manipulation by

1 degree-of-freedom manipulator. In Proceedings of

the IEEE/RSJ International Conference on Intelligent

Robots and Systems, volume 1, pages 132 –137.

Tahara, K., Maruta, K., Kawamura, A., and Yamamoto, M.

(2012). Externally sensorless dynamic regrasping and

manipulation by a triple-ﬁngered robotic hand with

torsional ﬁngertip joints. In Proceedings of the IEEE

International Conference on Robotics and Automation

(ICRA), pages 3252 –3257.

Tournassoud, P., Lozano-Perez, T., and Mazer, E. (1987).

Regrasping. In Proceedings of the IEEE International

IJCCI2014-DoctoralConsortium

Conference on Robotics and Automation, volume 4,

pages 1924–1928.

Vinayavekhin, P., Kudohf, S., and Ikeuchi, K. (2011). To-

wards an automatic robot regrasping movement based

on human demonstration using tangle topology. In

Proceedings of the IEEE International Conference on

Robotics and Automation (ICRA), pages 3332 –3339.

Xue, Z., Zollner, J. M., and Dillmann, R. (2008). Planning

regrasp operations for a multiﬁngered robotic hand. In

Proceedings of the IEEE Conference on Automation,

Science and Engineering, pages 778–783. IEEE.

Yashima, M. and Yamaguchi, H. (2002). Dynamic motion

planning whole arm grasp systems based on switch-

ing contact modes. In Proceedings of the IEEE In-

ternational Conference on Robotics and Automation,

volume 3, pages 2492 –2499.

AComputationalAlgorithmforDynamicRegraspingUsingNon-dexterousRoboticEnd-effectors