Ontology Hierarchy Self Generation using Algebraic
Multi-Grid (AMG)
Radel Ben-Av
Software Engineering Department, Azrieli College of Engineering,
POB 3566, Jerusalem, 91035, Israel
Abstract. In Computer Science an ontology is a standardized representation of
knowledge as a set of concepts within a domain, and the relationships between
those concepts. This can be described as a graph or a network. In this paper we
claim that the topology itself of the ontology contains significant semantics.
Then we discuss the possibility of revealing a hierarchy of element-class from
the network itself of an abstract ontology. We will use the Algebraic-Multi-Grid
(AMG) concepts and tools for the Laplace equation defined on this network.
1 Introduction
An ontology is a body of formally represented knowledge based on a
conceptualization: the objects, concepts, and other entities that are assumed to exist in
some area of interest and the relationships that hold among them [1]. An example of a
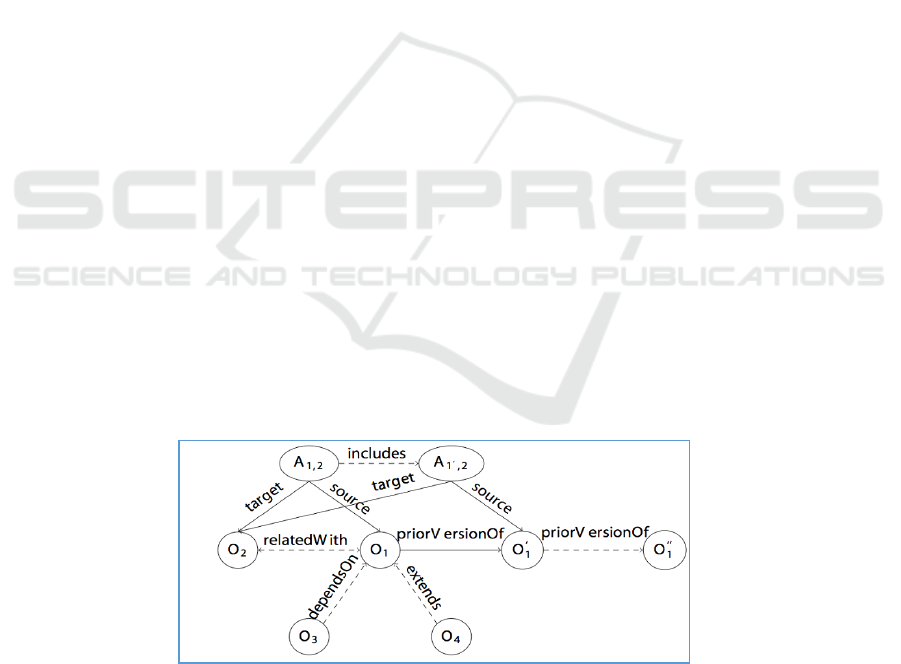
small fraction of an ontology is shown in Figure 1.
Fig. 1. An example of an ontology for software components.
It turns out that we can gradually eliminate information about the relationships among
concepts – e.g. relationship labels and/or relationship directionality – and still
preserve significant amounts of semantics in abstract ontologies containing only
concept labels.
The central idea of this work is to look at abstract ontologies as networks
amenable to algebraic treatment, viz. by AMG methods, ultimately leading back to
semantic gains.
Algebraic Multi-Grid (AMG) [4] is a family of numerical methods that was
Ben-Av R..
Ontology Hierarchy Self Generation using Algebraic Multi-Grid (AMG).
DOI: 10.5220/0005182400790085
In Proceedings of the 5th International Workshop on Software Knowledge (SKY-2014), pages 79-85
ISBN: 978-989-758-051-2
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

developed in order to accelerate computations for Linear and Non-Linear sets of
equations with many (hundreds of thousands and more) of variables. The Algebraic
MultiGrid method was developed over the past 40 years and proved useful in many
cases. The general idea behind the method is based upon constructing a hierarchy of
variables such that a coarser level has less variables than its finer level. The
connections between these coarse level variables is extracted from the finer level
variables that they represent. Eventually the coarsest level contains only few variables
and are easily solved. The solution is than down-propagated to the finer levels.
In this paper we explore Ontology hierarchy self-generation, starting from
abstracted ontologies, using AMG inspired methods.
1.1 Related Work
Here, a very concise review of related work is provided.
This work is within the field of automatic ontology summarization. Peroni,
Motta, and d’Aquin [2] describe such an algorithm based on number of criteria, drawn
from cognitive science, network topology, and lexical statistics.
Tho, Quan Thanh, et al [3] describe how to build an ontology from text with
ideas that are similar to some of the ideas in this paper however without the algebraic
infrastructure.
Clustering based on eigenvalues of the some similarity matrix is found in [4,5].
The AMG approach is similar to the algebraic approaches since it is also related to
eigenvectors with low eigenvalues. However the spectral methods completely ignore
any information that is coded in the “geometrical” nature of the network whereas the
AMG is trying to encompass it in a hierarchal fashion.
2 From Ontology to Abstract Networks
When one deals with an ontology one perceives the property that some "concepts"
(nodes) are related to each other such that they form a “group” – or as we would like
to formalize it a new ontology element emerges such it will be a “class” where the
elements in the group would now be elements in the "class". The process may be
repeated several times. Several levels of element-class relation would emerge.
In order to illustrate the claim let's look at figure 2.
Fig. 2. Moving objects ontology: animals in the l.h.s. and vehicles in the r.h.s.
Claim : The topology itself of the ontology contains significant semantics.
80

Even when we ignore the labels on the links it is clear that a "horse" is not related
to "Honda" and that "Hybrid" is remotely related to "Hyundai". Hence in order to
simplify (and actually to enable) the following discussion we will ignore the
relationship labels and will not discern between several types of relationships but
rather will discuss a general form of “relation”. Moreover, we claim that a significant
part of the information is preserved when we ignore the directionality of the relations
(this constraint is not an absolute must, but it simplifies the discussion). Hence we are
dealing now with an undirected graph. Figure 3 is the undirected graph of Figure 1.
Fig. 3. Ontology abstract network. This is the same ontology as in Fig. 1 with removed
relationship labels and directionality.
In a real semantic ontology network several hierarchies may co-exist over a single
network, each class would represent a different set of “relations”. E.g. “dog” may be
an element in the class of “canine” and also a member of the class “three letters
word”.
3 Laplace Equation
The first step in our algebraic treatment is to define a set of linear equations based on
the network. One of the natural candidates is the Laplace equation. This will be
briefly explained in the following section. The important aspect is that there is a
variable for each node. An equation for each node is also built from the variable in the
node and the variables of the nodes adjacent to this node. An elaborated version can
be found in [7]. The non-expert can skip section 3.1.
3.1 Laplace Equation – Definition
Let us define a variable x
i
for each node (concept/object) in the network. Let A
i,j
be
the adjacency matrix. That is A
i,j
=1 if and only if the i's object is related to the j's
object, otherwise A
i,j
=0. Now let us define D to be a diagonal matrix such that
That is D contains on the diagonal the number of neighbours of the node i.
That is D contains on the diagonal the number of neighbours of the node i.
(1)
.
j
ii
D
ji,,
A
81

The un-normalized Laplace operator over the network I is now defined as
L=D-A. and the set of equations is
fLx
. (2)
When f=0, eq (1) has a simple interpretation. It states that the value at the node i
(x
i
) equals the average of its neighbors (the elements j such that A
i,j
=0).
The normalized versions of the laplacian operator are
fLxDL
rw
1
. (3)
and
fxLDDL
sym
2/12/1
(4)
In the following we will refer to definition (2). The rest of the discussion can be
adapted to (3) and (4) and verify that at least qualitatively they bring similar results.
4 Algebraic Multi-Grid in a Nutshell
Algebraic Multi Grid (AMG) [6] is a variant of the Multi-Grid methods. The Multi-
Grid (MG) methods were formed in order to solve a set of differential equations
usually related to some physical problem. The approach is based on representing the
problem on small scales and on large scales (see figure 4). The small scale provides
the required accuracy where the large scale would provide the faster convergence. In
the geometrical MG the small and large scales are extracted using the given geometry
of the problem. In Algebraic MG the small and large scales are constructed during the
solution process using the equations themselves.
Thus the AMG methods contain an additional step – define the coarse degrees of
freedom based on the equations themselves without external reference to the
geometry (if it exists). The AMG methods contain a step of recursively defining
coarse degrees of freedom using the knowledge that is embedded in the equations
defining the problem at hand.
Fig. 4. MultiGrid scheme. The fine level (h) is transferred to the coarser level (2h), and then
recursively until the coarsest level is reached. Then backwards the solution is transferred to the
finer level etc. until the finest level is reached again.
5 AMG and Ontology Networks
In this work we suggest to use the Algebraic Multi-Grid [6] both as a set of concepts
and as a practical tool for defining an hierarchy of element-class. Each level will be
82

formed in two steps:
1. ”Class objects” –will be defined based on the structure of the network of
relations of the current level, such that the elements will be members of these
classes.
2. Class relations – The relations between the classes will be automatically
generated based on the relations of the elements that form the class and their
relations.
The first step for each level is achieved by decomposing the elements of this level
into two disjoint subsets: Coarse elements and Fine elements. Technically it can be
thought of a coloring process were each element is colored wither by “C” or by “F”.
The coloring is required to fulfil two requirements:
R1: each "F" element should have at least one "C" element that is strongly
connected to it;
R2: "C" elements should not be strongly connected to each other.
There are a few heuristics that strive to optimize this step.
In the second step a new set of equations is built between the coarse points. This
set of equations is a coarse representation of the fine equations such that solving this
set is a coarse solution to the fine equations.
It is important to understand that after repeating the process once or more, then the
set of equations that are generated in the higher level are not anymore a “simple”
Laplacian. The strength of the elements L(i,j) in higher levels are not anymore
restricted to be 0 or 1. They now represent in a finer degree the strength of connection
between these “higher-level” elements.
The coarse elements of the current level will now be considered elements of the
next level and the process of forming “super classes” can now be continued until only
a single class is remained.
Note: The AMG process depends only on the equations and not of the required
outcome. That is for equation (3) the process depends only on L and not on f.
5.1 Overall AMG Procedure
The overall AMG Procedure in pseudo-code is:
Start from a network of concepts N as explained in section 2.
Using the network N define a set of equations (the Laplace equation) as
explained in section 3.
On this set of equations we apply the AMG method. A central component of
the AMG method is the construction of a multi-level structure of coarse and
fine variables. The coarse variables at each level represent a set of variables
in the lower level (the fine points).
In the ontology language, we will claim that this process creates a hierarchy such
that the coarse "concept" is representing the concepts in the hierarchy below it. At this
point it is important to state that we do not impose from the outside how many levels
are needed nor how many fine elements are represented by any coarse element (even
though these numbers can be controlled using some parameters of the heuristics).
83

6 Discussion
In a formal sense we could measure to which degree does this "coarsening" do justice
or is this particular choice of coarse/fine (or class/element) relations faithful to the
intended semantics. This metric could measure whether solving the coarse equation
on the coarse level contributes to the solution of the fine level after a lower
(interpolated) level. Again formally, we should measure if the AMG process is more
efficient than say a simple Gauss-Seidel process for the same topology. If it is - we
will claim that the coarsening procedure represents (at least in some sense) the finer
level.
In the spirit of the paper published in SKY2010 [8], we could also claim that we
have extracted information about the system since we are now able so solve it faster.
6.1 Open Issues and Future Work
There is a series of interesting open issues to be dealt with in future work:
How do we “test” whether the scheme succeeded to capture the multi-level
structure of the ontologies from?
Is the obtained hierarchy semantically meaningful?
When the AMG scheme is expected to break down and when it is expected to
succeed?
Finally, to implement the method in a tool, to enable performance of actual tests,
initially with small, abstract case studies, which will be gradually increased to actual
practical problems.
Acknowledgements
I am grateful to Iaakov Exman for very fruitful discussions and important contribution
for this work.
References
1. Genesereth M. R. and Ketchpel S.P., “Software agents”. Communications of the ACM,
37(7):pp. 48-53, (1994).
2. Peroni, S., Motta, E., and d’Aquin, M., “Identifying key concepts in an ontology, through
the integration of cognitive principles with statistical and topological measures”, in The
Semantic Web,pp. 242-256, Springer Berlin Heidelberg (2008).
3. Tho, Quan Thanh, et al. "Automatic Fuzzy Ontology Generation for Semantic web." IEEE
Transactions on Knowledge and Data Engineering 18.6 (2006).
4. Ng, A. Y., Jordan, M. I., & Weiss, Y “On spectral clustering: Analysis and an algorithm”
Advances in neural information processing systems, 2, 849-856 (2002).
5. Chin C. F, Shih A. C. C, & Fan, K. C. A, “Novel Spectral Clustering Method Based on
Pairwise Distance Matrix”, J. Inf. Sci. Eng., 26(2), pp. 649-658, (2010).
6. Falgout R.D., “Introduction to Algebraic Multigrid”, Computing in Science and
Engineering #8 pp. 24–33, (2006).
84

7. Belkin M. and Partha N., “Laplacian eigenmaps and spectral techniques for embedding and
clustering", NIPS. Vol. 14. (2001).
8. Ben-Av R., “Physical Knowledge - Computability and Complexity”, in Proc. 1
st
SKY
International Workshop on Software Knowledge, June 16-17, Herzelia, Israel (2010).
85
