
Semantic Relatedness with Variable Ontology Density
Rui Rodrigues
1
, Joaquim Filipe
1
and Ana L. N. Fred
2
1
Escola Superior de Tecnologia, Instituto Polit
´
ecnico de Set
´
ubal, Set
´
ubal, Portugal
2
Instituto de Telecomunicac¸
˜
oes, Instituto Superior T
´
ecnico, Lisboa, Portugal
Keywords:
Semantic Relatedness, Wikipedia Categories, Ontological Entities, Taxonomical Density.
Abstract:
In a previous work, we proposed a semantic relatedness measure between scientific concepts, using Wikipedia
categories network as an ontology, based on the length of the category path. After observing substantial dif-
ferences in the arc density of the categories network, across the whole graph, it was concluded that these
irregularities in the ontology density may lead to substantial errors in the computation of the semantic re-
latedness measure. Now we attempt to correct for this bias and improve this measure by adding the notion
of ontology density and proposing a new semantic relatedness measure. The proposed measure computes a
weighed length of the category path between two concepts in the ontology graph, assigning a different weight
to each arc of the path, depending on the ontology density in its region. This procedure has been extended to
measure semantic relatedness between entities, an entity being defined as a set of concepts.
1 INTRODUCTION
The semantic relatedness between two concepts indi-
cates the degree in which these concepts are related
in a conceptual network, by computing not only their
semantic similarity but actually any possible seman-
tic relationship between them (Ponzetto and Strube,
2007) (Gracia and Mena, 2008).
Computational semantic relationship techniques
can be placed into one of two categories:
• Distributional measures that rely on unstructured
data, such as large sets. The underlying assump-
tion is that if similar words appear in similar con-
texts, then they should have similar meanings.
• Measures based on structured databases, such as
taxonomies or ontologies, where semantic rela-
tionships are captured.
This work focuses on the second relationship mea-
suring category, and uses Wikipedia page categories
as a taxonomy.
The proposed measure considers not merely the
number of arcs in the graph between the nodes that
represent each concept, but also their relationship in
the taxonomy. In our work we used the English ver-
sion of Wikipedia
1
, based on which we analyzed re-
lationships between concepts by building paths from
start to destination nodes in the category network.
1
http://en.wikipedia.org
This procedure has been extended to measure seman-
tic relatedness between entities, an entity being de-
fined as a set of properties, i.e. concepts.
Since the Wikipedia ontology is in constant de-
velopment, it was observed that some regions are far
more developed than others. In this paper we pro-
pose to add to our previously developed measure of
semantic relatedness (Medina et al., 2012) the no-
tion of density, as a function of the number of incom-
ing and outgoing links to/from a node in the concep-
tual graph. This means that the semantic relatedness
between concepts needs is inversely weighed by the
density of the region of the path between concepts.
We will propose a technique to compute the density
of this region.
The remaining sections of this document are or-
ganized as follows: in Section 2 we describe related
work in this area; Section 3 presents the proposed
measure of semantic relatedness with the inverse den-
sity ponderation and in section 4 are presented the re-
sults obtained after applying this measure to a set of
entities. Finally, in Section 5 we draw the main con-
clusions and identify opportunities for future work.
2 RELATED WORK
Given two words or expressions represented in a tax-
onomy, the computation of the semantic relatedness
554
Rodrigues R., Filipe J. and L. N. Fred A..
Semantic Relatedness with Variable Ontology Density.
DOI: 10.5220/0005189005540559
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (SSTM-2014), pages 554-559
ISBN: 978-989-758-048-2
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

between these two objects may be transformed into
the evaluation of their conceptual distance in the con-
ceptual space generated by a taxonomy (Jiang and
Conrath, 1997), being that each object is represented
by a node in the resulting graph.
Semantic relatedness measures in hierarchical tax-
onomies can be categorized into three types (Slimani
et al., 2006):
1. Information Content or Node-based: evalua-
tion of the information content of a concept rep-
resented by a node such as described in (Resnik,
1999). The semantic relatedness between two
concepts reflects the amount of shared informa-
tion between them, generally in the form of their
least common subsumer (LCS).
2. Path or Edge-based: evaluation of the distance
that separates concepts by measuring the length
of the edge-path between them (Wu and Palmer,
1994) (Rada et al., 1989). A weight is assigned
to each edge, being that the weight computation
must reflect some of the graph properties (network
density, node depth, link strength, etc.) (Jiang and
Conrath, 1997)
3. Hybrid: a combination of the former two (Jiang
and Conrath, 1997) (Leacock and Chodorow,
1998).
Lexical databases, such as WordNet, have been
explored as knowledge bases to measure the semantic
similarity between words or expressions. However,
WordNet provides generic definitions and a somewhat
rigid categorization that does not reflect the intuitive
semantic meaning that a human might assign to a con-
cept.
In this paper we use the english version of the
Wikipedia
2
, a web-based encyclopedia which has ap-
proximately 4 million articles edited and reviewed by
volunteers. The contributors are asked to assign these
articles to one or more categories: Wikipedia may
be thus viewed as either a folksonomy (Nastase and
Strube, 2008) or a Collective Knowledge Base (Zesch
et al., 2008), where human knowledge and human in-
tuition on semantic relationships emerges in the form
of a category network. It is then natural that this web-
resource has been increasingly explored as a concep-
tual feature space, such that articles and categories are
represented as nodes in the Wikipedia graph.
Techniques such Explicit Semantic Analysis
(ESA) (Gabrilovich and Markovitch, 2007) repre-
sent texts in the high-dimensional concept space of
Wikipedia as weighted vectors. A textual fragment
is thus considered as a weighted mixture of a prede-
termined set of ”natural” concepts. Wikipedia Link-
2
http://en.wikipedia.org
based Measure (WLM), first described in (Milne and
Witten, 2008), uses its hyperlink structure, rather than
the category hierarchy or textual content to compute
semantic relatedness. In (Gouws et al., 2010) seman-
tic relatedness is computed by spreading activation
energy over the aforementioned hyperlink structure.
Measurement of semantic similarity between con-
cept sets can provide particular value for tasks con-
cerning the semantics of entities (Liu and Birnbaum,
2007). An entity may represent, for instance, (1) an
author, by means of his/her research interests, (2) a
publication, such as a scientific journal, by means of
its main topics, (3) a conference, by means of its sub-
mission topics. In Information Retrieval, the simi-
larity between documents is generally estimated by
means of their Vector Space Models. Each feature
vector represents the bag-of-words of the respective
document, assigning a weight to each feature/term
that reflects its importance in the overall context of
either the document or the document set. The def-
inition of entity can also be extended to represent a
document, where instead of a weighted feature vec-
tor, we have a set of terms that can be related to other
entities (which may also be documents or other types
of entities) by means of a semantic relatedness mea-
sure between entities, such as the one presented in this
paper.
3 SIMILARITY RELATEDNESS
MEASURE
The implementation of the proposed measure is based
on the assumption that each pair of concepts is con-
nected by a category path.
The proposed relatedness measure is computed
from the following sequence of steps
Distance between Concepts - Weighted Edges
Sum. Let c
1
and c
2
be two concepts represented in
the Wikipedia categories network. Find the shortest
category path between the concepts. Compute the
edge-based semantic relatedness between c
1
and the
LCS node, which is the sum of the weights of the
edges that link c
1
to the LCS node. Repeat this proce-
dure to find the edge-based semantic relatedness be-
tween c
2
and the LCS node.
The overall edge-based relatedness measure be-
tween the two concepts is given by
d(c
1
, c
2
) =
∑
I
i=0
w
1
i
+
∑
J
i=0
w
2
i
∑
R
i=0
w
1
i
+
∑
R
i=0
w
2
i
(1)
where w
1
i
is the weight of the edge with index i in
SemanticRelatednesswithVariableOntologyDensity
555

the category path between c
1
and the LCS category,
w
2
i
is the weight of the edge with index i in the cate-
gory path between c
2
and the LCS category, I is the
depth of the last edge of the path that connects c
1
to
the LCS and J is the depth of the last edge of the path
that connects c
2
to the LCS category, with R denoting
the index of the last edge in the path between the root
node and a concept node, with the restriction that this
path must include the LCS.
Edge-based Similarity between Entities. Given
two entities E
1
and E
2
represented by discrete sets of
concepts C
1
= {c
1
1
, ..., c
1
n
} and C
2
= {c
2
1
, ..., c
2
m
}, re-
spectively, we define the edge-based distance between
sets D(E
1
, E
2
) is
D(E
1
, E
2
) =
∑
n
i=1
∑
m
j=1
d(c
i
, c
j
)
n × m
(2)
Finally, we have the following similarity measure
between entities
S(E
1
, E
2
) = 1 − D(E
1
, E
2
) (3)
3.1 Computation of Shortest Paths in
the Wikipedia Graph
Several versions of the Wikipedia maybe be accessed
at http://dumps.wikimedia.org/backup-index.html.
For the results presented in this paper, we used a
recent english version. To store all the Wikipedia
pages and links we used the MySQL structure pro-
vided by the Java Wikipedia Library API (available
at http://www.ukp.tu-darmstadt.de/software/jwpl/),
further described in (Zesch et al., 2008). This API
also helps us to determine if a page is of the ”Dis-
ambiguation pages” type. We did not, however, used
the API to build category paths, having specifically
devised procedures for this task.
Each Wikipedia object of the type CATEGORY is
assigned a level within the current search and a list
of its nearest neighbors, when examined for short-
est path computation. By regarding this shortest-path
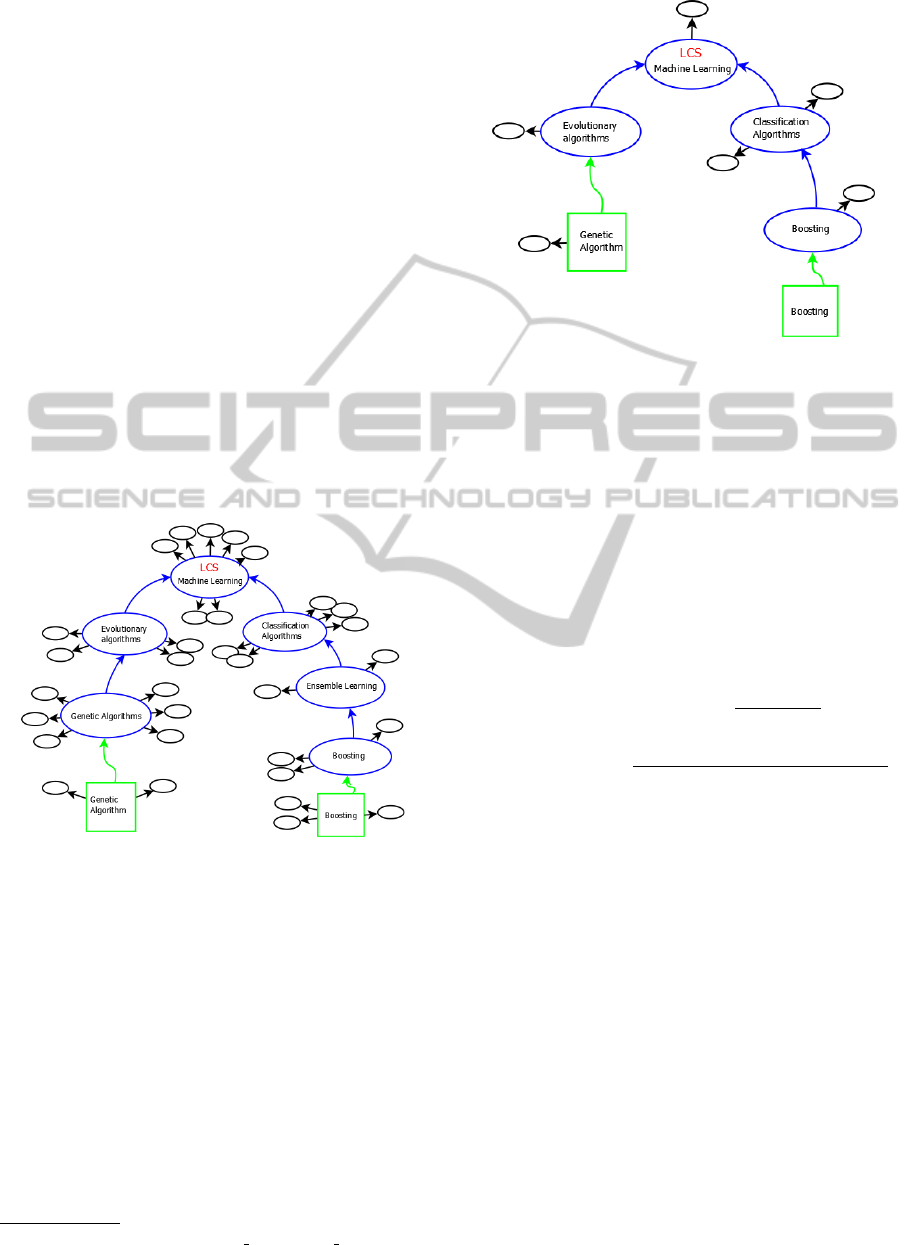
Figure 1: Instatiation of the concept ”Machine Learning”.
search as a tree-search, each instance of the object cat-
egory will be a leaf of the tree.
1 C a t ego r y n e x t L e v e l ( C a t e g or y c )
2 Begin
3 Fo r E a c h C a t e g or y in c . List
4 Begin
5 If ( I t e r a t e d C a t e g o r y . List = null )
-> l e a f n o d e
6 Begin
7 Wi k i L i st = wiki p e d ia .
Ge t Ab o v e L e v e l C a t e g o r i e s
() ;
8 c. L i s t = newL i s t ;
9 End
10 Else
11 Begin
12 N e x t L ev e l ( I t e r a t ed C a t e g o r y );
-> re c u r si v e met h o d
13 End
14 End
15 End
Listing 1: Procedure to examine the upper level of a node.
After the instantiation of concept Machine Learn-
ing (see Figure 1), all of its parent categories (”Ar-
tificial Intelligence”, ”Learning” and ”Computational
Statistics”) will have a level attribute of two. The in-
statiation of each of these categories will return their
corresponding list of parent categories and a level at-
tribute of 3 and so on. The pseudo code in Listing 1
illustrates this procedure.
For each computation of a category path between
two concepts, two trees are built, one for each con-
cept. The level attribute will grow until the algorithm
finds a common ancestor (the LCS).
1 Void Main ( )
2 Begin
3 List c 1 = w i k i pe d i a .
Ge t Ab o v e L e v e l C a t e g o r i e s (" c o n c ept 1 ")
;
4 List c 2 = w i k i pe d i a .
Ge t Ab o v e L e v e l C a t e g o r i e s (" c o n c ept 2
") ;
5
6 While ( E xi s t M a t c h (c1 , c2 ) )
7 Begin
8 ne x t L e ve l ( c 1 ) ;
9 ne x t L e ve l ( c 2 ) ;
10 End
11 End
Listing 2: Procedure to find a path by means of a least
common subsumer search.
The pseudo code in Listing 2 illustrates this pro-
cedure for example concepts ”concept1” and ”con-
cept2”.
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
556
These procedures were implemented with Java.
Java is not the most adequate technology for this type
of tree search, since it lacks tail call elimination for se-
curity reasons, as further detailed in the Bugs section
of Oracles website
3
but it was sufficiently effective to
accomplish our goals.
3.2 Density
The general idea behind the proposed improvement
to the measure can be introduced with some generic
mathematics concepts. In graph theory, a dense graph
is a graph in which the number of edges is close to the
maximal possible between all the vertices contained.
The maximum density is 1 and the minimum is 0
for a very sparse graph (Coleman and Mor
´
e, 1983).
In our case, we do not intend to calculate the com-
plete density of the Wikipedia category ontology. In-
stead, we propose to analyse all the nodes in the short-
est path and find all the degrees. Then it is necessary
to find a way of discover the approximate level of den-
sity with the degrees as a clue.
Figure 2: Example of an High Density path.
In the figure above, the larger circles represents
Wikipedia categories in the path, the small ones rep-
resent the neighbors and the squares represents the
Wikipedia pages. As it can be observed, Figure 2 rep-
resents a situation of higher density than Figure 3 and
as we can conclude, the number of degrees for each
node follows the tendency.
When path calculation occurs, the degrees of all
vertices in the calculated path are saved, even the
number of categories at the original pages.The objec-
tive is to save as much information as possible about
the number neighbors of the calculated path. As it
was previous explained, the properties of our entities
were mapped to the correct page that represents the
3
See http://bugs.sun.com/view bug.do?bug id=4726340
Figure 3: Example of a Low Density Path.
concept in Wikipedia. Figure 2 aims to find the dis-
tance between the property generic algorithm and the
property boosting. These two concepts are contained
in two different sets of properties, each one represent-
ing it own entity.
For every path explored between the entity prop-
erties the average number of neighbors is calculated.
This means that information about the average num-
ber of nodes that are between the two entities is kept
across the paths calculations, and based on that, al-
lows to understand if the universe that we are working
at the moment is more or less dense.
PathDensity(p1, p2) =
∑
n
1
| E | (i)
n
(4)
PropertyDensity =
PathDensity(p1, p2)
PathDensity(p1, p2)+RootDensity(lcs,root)
(5)
On top of that, as we saw before, the LCS node is
very important to us. In a previous work it was con-
cluded that it is very helpful to calculate how deep is
this node (Medina et al., 2012). Now we propose to
use additional information, by taking into account the
density of the path between a given LCS and the root.
The strategy is similar to the density calculation prop-
erty, with the difference that now our path is between
our LCS and the Wikipedia root category. We count
the neighbors at each vertex and calculate the average
at the end.
4 RESULTS AND DISCUSSION
With test result tracking in mind, we decided to use
the same battery of entity tests from last paper (Med-
ina et al., 2012). The results can be consulted on table
SemanticRelatednesswithVariableOntologyDensity
557

Table 1: Entities represented as sets of scientific topics. The first three entities represent actual conferences (CVPR, KDD and
RECOMB respectively). The other three entities represent authors.
E1 E2 E3 E4 E5 E6
Computer Vision Knowledge Discovery Molecular Biology Computer Vision Information Extraction Genetics
Object Recognition Data Mining Gene Expression Robotics Machine Learning Human Genome
Structure from Motion Web Mining Computational Biology Object Recognition Natural Language Processing Gene Expression
Image Segmentation Recommender Systems Genomics Structure from Motion Information Retrieval Systems Biology
Image Processing Cluster Analysis Population Genetics Human Computer Interaction Data Mining Clinical Medicine
Object categorization Text Mining Virtual Reality Graphical Model Bioinformatics
Optical Flow Data Analytics Facial Expression Social Network
Pattern Recognition Structure Mining Reinforcement Learning
Web Mining
Table 2: Proposed similarity measure results.
Pair (E
1
, E
4
) (E
1
, E
5
) (E
1
, E
6
) (E
2
, E
4
) (E
2
, E
5
) (E
2
, E
6
) (E
3
, E
4
) (E
3
, E
5
) (E
3
, E
6
)
S Eq.3 0.948 0.931 0.912 0.869 0.954 0.826 0.786 0.862 0.989
S Den 1.0 0.958 0.682 0.812 1.0 0.724 0.847 0.826 1.0
2, where the first row contains the values previously
obtained on our first paper, and the second row con-
tains the results achieved by the new method. The
set is composed by six entities: three of them rep-
resent well known conferences (CVPR
4
, KDD
5
and
RECOMB
6
). These conferences were chosen because
each one corresponds to a distinct scientific research
area: CVPR to Computer Vision and Pattern Recog-
nition; KDD to Data Mining and Knowledge Discov-
ery; RECOMB to Computational Molecular Biology.
The other three entities represent well known authors.
Each of these authors was chosen based on the strong
correspondence of their research interests with one of
the three conferences:
• Author E
4
: from computer vision area, which
matches CVPR represented by E
1
.
• Author E
5
: from data mining and machine learn-
ing areas, which are more related to the KDD, rep-
resented by E
2
.
• Author E
6
: from genetics and bioinformatics ar-
eas, which is more closely related to RECOMB
(represented by E
3
).
Some concepts listed here do not have a direct cor-
respondence with a Wikipedia page, so it lead us to a
disambiguation problem. A quick solution for the first
case was to replace the concept with a similar con-
cept. For instance, the concept Image Segmentation
of E1 had to be replaced with the page Segmentation
(image processing). We will propose a technique to
automation this kind of tasks in a future work.
From these results, as before, we observed a high
value of similarity for the following entity pairs:
4
http://www.cvpr2012.org/
5
http://kdd2012.sigkdd.org/
6
http://bioinfo.au.tsinghua.edu.cn/recomb2013/
(E
4
, E
1
), (E
5
, E
2
), and (E
6
, E
3
), but at this time, there
is even stronger. This is expected due to the semantic
overlapping of properties in the sets. It was also ex-
pected that the similarity values for (E
1
, E
5
) would be
much lower than the value found for (E
1
, E
4
). It was
observed that in many cases this distance continues
to return very high similarity values that are not quite
differentiated. We believe this is due to the proxim-
ity of a single pair of features, among many features.
The fact that similarity between entities is determined
by the maximum value of the similarity between all
combinations of pairs of entities features introduces
”bias” to 1. Hence it is needed, eventually, in the fu-
ture to introduce mechanisms to extend the dynamic
range of the similarity between entities. However, the
high similarity E1-E5 is explained due to some very
similar features, such as Pattern Recognition vs. Ma-
chine Learning, for example.
5 CONCLUSIONS AND FUTURE
WORK
In this paper we continue our journey to find a more
balanced semantic relatedness measure between enti-
ties. As before, we belive that the use of Wikipedia
and the hierarchy of scientific categories contained in
it, is the most promising way to accomplish your goal.
The devised measure examines the Wikipedia cat-
egory paths between all the possible concept pairs of
two distinct entities, assigning weights according to
the category’s relevance. With this new attempt, we
improve this measure by adding the notion of ontol-
ogy density. We examined and compared new results
with the old ones and concluded, by observing, that
these matchs are a step in the right direction. Altough
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
558

there is room for future developments, mainly regard-
ing the range of result values, the differentiation of
values and eventually the introdution of a threshold.
The issue is to determine where to place the threshold
to make the right decision. Usually the threshold is
set ”half-way”, however, for this test case, it should
be placed above 0.73, which is a high value.
Future work includes continuing exploration of
the measure for other contexts as well as a compari-
son of our measure with other state-of-the-art metrics.
It is also very important the effort to make the process
as much autonomous as possible, by giving to the pro-
cess the ability of automatic disambiguation.
ACKNOWLEDGEMENTS
The authors wish to acknowledge the support
of the Escola Superior de Tecnologia, Instituto
Polit
´
ecnico de Set
´
ubal (EST-IPS) and Instituto de
Telecomunicac¸
˜
oes (IT-IST).
REFERENCES
Coleman, T. F. and Mor
´
e, J. J. (1983). Estimation of sparse
Jacobian matrices and graph coloring problems. SIAM
Journal on Numerical Analysis, 20(1):187–209.
Gabrilovich, E. and Markovitch, S. (2007). Computing se-
mantic relatedness using wikipedia-based explicit se-
mantic analysis. In Proceedings of the 20th inter-
national joint conference on Artifical intelligence, IJ-
CAI’07, pages 1606–1611. Morgan Kaufmann Pub-
lishers Inc.
Gouws, S., Rooyen, G., and Engelbrecht, H. (2010). Mea-
suring conceptual similarity by spreading activation
over wikipedia’s hyperlink structure. In Proceedings
of the 2nd Workshop on The People’s Web Meets NLP:
Collaboratively Constructed Semantic Resources.
Gracia, J. and Mena, E. (2008). Web-based measure of se-
mantic relatedness. In In Proc. of 9th International
Conference on Web Information Systems Engineering
(WISE 2008), Auckland (New Zealand, pages 136–
150. Springer.
Jiang, J. J. and Conrath, D. W. (1997). Semantic Similarity
Based on Corpus Statistics and Lexical Taxonomy. In
International Conference Research on Computational
Linguistics (ROCLING X).
Leacock, C. and Chodorow, M. (1998). Combining Local
Context and WordNet Similarity for Word Sense Iden-
tification, chapter 11, pages 265–283. The MIT Press.
Liu, J. and Birnbaum, L. (2007). Measuring semantic sim-
ilarity between named entities by searching the web
directory. In Proceedings of the IEEE/WIC/ACM In-
ternational Conference on Web Intelligence, WI ’07,
pages 461–465.
Medina, L. A. S., Fred, A. L. N., Rodrigues, R., and Filipe,
J. (2012). Measuring entity semantic relatedness us-
ing wikipedia. In Fred, A. L. N., Filipe, J., Fred, A.
L. N., and Filipe, J., editors, KDIR, pages 431–437.
SciTePress.
Milne, D. and Witten, I. H. (2008). An effective, low-
cost measure of semantic relatedness obtained from
wikipedia links. In In Proceedings of AAAI 2008.
Nastase, V. and Strube, M. (2008). Decoding wikipedia
categories for knowledge acquisition. In AAAI, pages
1219–1224.
Ponzetto, S. P. and Strube, M. (2007). Knowledge derived
from wikipedia for computing semantic relatedness. J.
Artif. Int. Res., 30:181–212.
Rada, R., Mili, H., Bicknell, E., and Blettner, M. (1989).
Development and application of a metric on semantic
nets. IEEE Transactions on Systems, Man and Cyber-
netics, 19(1):17–30.
Resnik, P. (1999). Semantic Similarity in a Taxonomy:
An Information-Based Measure and its Application to
Problems of Ambiguity in Natural Language. Journal
of Artificial Intelligence Research, 11:95–130.
Slimani, T., Yaghlane, B. B., and Mellouli, K. (2006). A
New Similarity Measure based on Edge Counting. In
Proceedings of world academy of science, engineer-
ing and technology, volume 17.
Wu, Z. and Palmer, M. (1994). Verbs semantics and lexical
selection. In Proceedings of the 32nd annual meeting
on Association for Computational Linguistics, ACL
’94, pages 133–138. Association for Computational
Linguistics.
Zesch, T., M
¨
uller, C., and Gurevych, I. (2008). Extract-
ing Lexical Semantic Knowledge from Wikipedia and
Wiktionary. In Proceedings of the Conference on Lan-
guage Resources and Evaluation (LREC).
SemanticRelatednesswithVariableOntologyDensity
559
