CFD Prediction of the Effect of Appendages and Leeway on the Force

Trend of an Olympic Class Laser Dinghy Hull

Rickard Lindstrand

, Jeremy Peter

and Christian Finnsgård

2,3

Department of Shipping and Marine Technology, Chalmers University of Technology, Gothenburg, Sweden

SSPA Sweden AB, Research, Gothenburg, Sweden

Centre for Sports Technology, Department of Applied Physics, Chalmers University of Technology, Gothenburg, Sweden

Keywords: CFD, Sailing, Verification & Validation, Tow Tank Testing.

Abstract: The purpose of this paper is to investigate whether the minima in hydrodynamic resistance can be predicted

to occur at the same angles of heel and trim in the case of bare hull towing tank tests, bare hull simulations

and appendage and leeway simulations. If so, the appendages and the leeway can be rejected from future

investigations, which would prove a beneficial advancement, as they impose further complexity to

simulations. The results of verification and validation (V&V) included in this paper demonstrate that the

numerical method predicted too low resistance. Though the study identifies and systematically investigates

possible sources of error, the major source of error was not found. These various possible sources of errors

were identified for further research, and as future references for similar cases. Moreover, the simulation

results for the variations of heel and trim also require further study. Before a full set of results is available,

one cannot make conclusions regarding the angles of heel and trim that lead to minimal resistance. This

paper discusses the results and potential avenues of future research, and is a result of an initiative at

Chalmers University of Technology focusing on sports and technology.

1 INTRODUCTION

As a result of the hull’s complex three-dimensional

shape, the flow around the dinghy will differ for

different attitudes to the direction of motion. This

implies the possibility of locating a minimum of

hydrodynamic resistance by sailing at a specific

angle of trim and heel. Finding the attitude of

minimum resistance can potentially increase

performance.

Hydrodynamic resistance is not the only effect

that must be considered when altering the angle of

heel and trim. The projected area for the centerboard

and rudder is decreased when the dinghy is heeled,

and this is the case for the sail as well. Moreover,

stability could be decreased when trimming on the

bow. These effects will not, however, be taken into

account in this paper.

Since the weight of the sailor represents more

than half of the displacement, the angles of heel and

trim are changed by positioning the dinghy’s sailor

in a certain manner.

At the professional level sailors perform

similarly, and thus possibilities like the sailor’s

position must be exploited in order to gain

advantage on the race course. There is little evidence

in the literature that an investigation along these

lines has been conducted before.

The hull used for this study is the Laser dinghy

(see www.laserinternational.org for a description), a

four-meter-long dinghy for one sailor. The Laser

class has been an Olympic discipline since the 1996

Summer Olympics in Atlanta, and is a strict one-

design class, which means that design alterations or

additions of any kind are prohibited. Therefore, the

manner in which the dinghy is sailed becomes ever

more important, and any improvements in sailing

practice will consequently improve performance in

competitive situations at the international level.

The study resulting with the current paper is a

part of an initiative at Chalmers University of

Technology. The Olympic motto, “Citius, Altius,

Fortius” (Latin for “Faster, Higher, Stronger”),

governs everyday life for many engineers, and for

the last few years Chalmers has supported a project

that focuses on the possibilities and challenges for

research combined with engineering knowledge on

the area of sports. The initiative has generated

190

Lindstrand R., Peter J. and Finnsgård C..

CFD Prediction of the Effect of Appendages and Leeway on the Force Trend of an Olympic Class Laser Dinghy Hull.

DOI: 10.5220/0005191101900202

In Proceedings of the 2nd International Congress on Sports Sciences Research and Technology Support (icSPORTS-2014), pages 190-202

ISBN: 978-989-758-057-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

external funding and has gained great acclaim within

Chalmers, among staff and students, in the Swedish

sports movement, in large companies, as well as

within SME’s. The project focuses on five sports:

swimming, equestrian, floorball, athletics, and

sailing.

The paper is composed as follows: Chapter 1

provides the background to the problem and a very

brief introduction to the basics of the mechanisms of

sailing, the methodology and tow tank test setup.

Chapter 2 governs the computational method, while

Chapter 3 adresses the numerical method. Chapter 4

and 5 recites the verification and Chapter 6 the

validation. Chapter 7 finalises the paer with the

concluding remarks.

1.1 Background

The governing equations for the dynamics of a fluid

are the Navier-Stokes equation (NS) and the

continuity equation. However, it is not possible to

fully resolve the flow around a ship, yacht or dinghy

with these equations (Larsson and Raven, 2010,

section: 9.7.1). This is due to the large separation of

scales in the domain and the computational effort

required to handle such a separation. While the

Laser dinghy is four meters long, the smallest scales

in the flow, the Kolmogorov scales, are a mere

fraction of a millimetre (Larsson and Raven, 2010).

As a result, the resolution of the discretized domain

must be incredibly fine in order to fully resolve the

flow (Feymark, 2013). The resolving of one of the

smallest turbulent scales requires approximately four

cells in each spatial direction.

For ship applications, the level of resolution must

therefore be limited to that which results in an

affordable number of cells. An increase in the cell

size leads to a loss of information regarding the

smaller turbulent structures. To compensate for this

loss of information, turbulence models and near-wall

function are introduced to the simulation.

Meanwhile, the temporal resolution is neglected all

together, as the flow’s average quantities are of

greater interest than its instant ones (Larsson and

Raven, 2010). For example, it may be more valuable

to know the average hydrodynamic resistance, rather

than the value at each hundredth of a second.

One criterion for neglecting the temporal

discretization is that the flow is considered steady, or

independent of time. The equations must therefore

be adjusted in order to handle averaged quantities.

This operation is called Reynolds time averaging,

and the new equation is termed the Reynolds time-

averaged Navier-Stokes equation (RANS). As the

flow case of the dinghy in flat water is in fact one of

steady flow, this paper will employ RANS

equations.

1.2 Mechanisms of Sailing

The sail can be understood as a thin wing profile.

The wing generates lift and drag, which are defined

as the force components that are perpendicular and

parallel, respectively, to the apparent wind. The

apparent wind is the wind experienced by the sail,

i.e., with the boat velocity included (see Figure 1).

The point at which the pressure field of the sail can

be substituted by one force vector is called the center

of effort. As the center of effort is dependent on the

pressure distribution, it is not easy to identify,

though its location can be estimated at the sail’s

surface center.

Figure 1: Wind speeds and directions. The leeway is the

difference between the heading and the true boat velocity.

The lift of the sail is the only component acting

in the yacht’s positive direction of motion, and is

therefore the only component contributing to

propulsion. Furthermore, only one component of the

lift is in turn completely aligned with the direction of

the yacht. In order for the yacht to move in the right

direction, this driving force component must balance

the hydrodynamic resistance of the hull, the

component of the drag generated by the sail aligned

with the opposite direction of the yacht, and the drag

generated from the rigging, deck equipment, etc.

The term leeway refers to the slight drift of a

moving sailing craft toward the leeward side, and is

the result of the misalignment of the resultant force

of the sail and the direction of motion. This drift is

angled in the leeward direction, hence the name

leeway. As the center of effort of the sail is not at the

same height as the center of pressure for the hull and

keel, a heeling moment will also be generated,

resulting in the heel angle.

CFDPredictionoftheEffectofAppendagesandLeewayontheForceTrendofanOlympicClassLaserDinghyHull

191

1.3 Methodology

Prior to the investigation of heel and trim variations,

a V&V study will be performed. This verification

and validation study will be conducted in order to

identify the amount of error to be expected from the

simulations, and consequently, their relative

trustworthiness. Section 4 will further explain the

verification procedure.

1.4 Towing Tank Test Setup

Preparation of the dinghy for tow tank testing

necessitated modifications. An aluminium frame

was fitted to the deck around the cockpit. This frame

provided a point at which to attach the towing device

and also served to accommodate the weights used to

position the dinghy in the desired attitude. The

appendages were also removed in order to facilitate

what will be called a bare hull case. The final

modification consisted of the addition of points at

which to attach string connected to the measuring

devices used to accurately measure heel and trim

during speed tests. Figure 2 display the test frame on

the deck.

Figure 2: Display of the towing tank test Laser. Photos by

SSPA.

The towing device is attached to the top of the

vertical aluminium profile. As the towing force is

not applied through the center point of the

hydrodynamic resistance, a trimming moment is

hereby introduced. This moment will not be similar

to an actual sailing case, as the towing point does not

coincide with the sail’s center of effort.

The arm of the towing devise was set up so as to

be horizontal for the static cases. This meant that at

higher speeds when the dinghy meets with a

considerable draft change, the arm would no longer

be horizontal, and the towing force would pull the

dinghy slightly downward. This would create an

increase in displacement, which would in turn affect

resistance. Thus, the simulations to be performed

could not be set to free sinkage and trim.

Due to limited testing time, the heel tests were

only performed as heel to starboard tests.

The brackets that help hold the frame in place are

located on the railing of the dinghy, as illustrated in

Figure 2b. As the heel angle increased, the starboard

side brackets began interfering with the spray from

the bow wave. They were therefore removed from

that side and from the test rerun, without

interference from the frame.

During the test runs, a bailing pump was added

on the flooring of the cockpit to guard against excess

water. This excess water was a product of the not

completely watertight self-bailer device, which was

given to leak by the reversal of the test setup back to

the starting position in the towing tank after each

run.

2 COMPUTATIONAL METHOD

2.1 Governing Equations

The equations that govern fluid flow are derived

from basic physical principles and described by the

mathematical statements of the conservation laws of

physics: the conservation of mass and momentum.

The Navier-Stokes equations are derived from the

conservation laws and from several underlying

assumptions, and are used to predict the resistance

forces that result from water pressure and viscous

effects.

Basic assumptions. The Navier-Stokes

equations are based on the assumptions that the fluid

is a continuum, that is, a continuous substance, as

opposed to an aggregate of discrete particles.

In the case of water, the flow is commonly

considered incompressible, rendering constant the

density ρ and the viscosity µ.

The Navier-stokes equation is then time averaged

in order to arrive at the RANS equation

Coordinate system. The simulations are not set

up to account for changes in sinkage or trim, as a

result of the unnatural trimming moment and the

vertical force component created by the towing

device. The simulation is also assumed to be steady,

that is, it is assumed the dinghy will not move

relative to waves or in time. In the global Cartesian

coordinate system employed here, the origin is at the

icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport

192

bow on the centerline at the undisturbed water level,

x is directed sternward, y is directed starboard and z

is directed vertically upward.

2.2 Turbulence

2.2.1 Turbulent Flow

Typically, the fluid flow around the hull of a moving

ship is turbulent. Turbulent flows are irregular,

random and three-dimensional. In such flows,

velocity and pressure change continuously, creating

within the flow a spectrum of turbulent structures.

Despite the irregular nature of a turbulent flow, it is

possible to resolve its behaviour with the Navier-

Stokes equations (Davidsson, 2003). However,

doing so requires that the spatial and temporal

discretizations are capable of capturing all scales in

the flow. This is not possible for ship applications,

as the smallest scales are minuscule in relation to the

length of the hull, and this in turn leads to

unreasonable computational effort.

To resolve the turbulent flow at issue in the cases

here, this study utilizes the Reynolds-averaged

Navier-Stokes equation (RANS). This requires that

the regular Navier-Stokes equations are averaged

over time, a task accomplished by decomposing the

instantaneous variables into a mean value  and a

fluctuating value ϕ′ :

Insertion of the decomposed terms from (1) into the

Navier-Stokes equations gives rise to the Reynolds-

averaged Navier-Stokes (RANS) equations. The

expression of the incompressible Newtonian fluid in

the Einstein notation is:

This allows for more attention to the mean values,

and less to the time histories; indeed, when solving

the Navier-Stokes equations, a very fine resolution

in time would be necessary in order to resolve the

unsteady turbulent flow.

2.2.2 Modelling Turbulence

In the equation (2) the term ′



′





appears from the

fluctuating values. Known as the Reynolds Stress

tensor, this term is an unknown. In order to close the

equation system and solve for all the unknowns, the

Reynolds stress tensor must be modelled. This is

commonly termed the closure problem.

There are various ways to model the Reynolds stress

tensor, including the use of algebraic models, one-

equation models, two-equation models, algebraic

stress models and Reynolds Stress models. Each of

these turbulence models varies in terms of

computational requirements, accuracy in turbulence

modelling and complexity.

Two turbulence models were implemented in the

software i: the two-equation Menter’s Shear Stress

Transport model (SST k-ω) and the explicit

algebraic stress model (EASM). A description of

these models is available below.

Menter’s SST k-ω model. Menter proposed the

SST k-ω model in 1992 in order to improve the

performance of the near-wall turbulence modelling

of the commonly used two-equation k-ε-model

(Menter, 1994). The SST k-ω model uses the

turbulent kinetic energy k, the turbulence frequency

ω = ε/ k (dimension: s

-1

) and the Boussinesq

assumption to compute the Reynolds stresses. The

Boussinesq assumption is the presumed relation

linking the Reynolds stress tensor to the velocity

gradients and the turbulent viscosity. When a

turbulence model uses the Boussinesq assumption, it

then qualifies as a “linear eddy viscosity model”.

This two-equation turbulence model uses one

modelled transport equation for each of the two

variables, k and ω. The ω-equation is derived from

the ε-equation in the k-ε-model by simply

substituting the relation ε=kω. Though these

equations are not displayed here in detail, it is

nevertheless important to understand the manner in

which these transport equations are constructed. For

both equations, the structure is as follows (Versteeg

and Malalasekera, 2007):

The SST k-ω model combines the benefits of the

Wilcox’s k-ω model at the near-wall and the

performance at the freestream and shear layers of the

k-ε model. This is why Menter’s SST k-ω model is

suitable for a wide range of CFD applications

(Rumsey, 2013). Additionally, assessments of this

turbulence model have suggested that it offers

superior performance in the case of an adverse

pressure gradient boundary layer (Versteeg and

Malalasekera, 2007). An adverse pressure gradient

leads to lower kinetic energy of the fluid, and hence

to a reduction of its velocity. If the pressure increase

is large enough, the fluid direction can be reversed;

this is what occurs in flow separation, a phenomenon

CFDPredictionoftheEffectofAppendagesandLeewayontheForceTrendofanOlympicClassLaserDinghyHull

193

that typically occurs at the transom of a boat like the

Laser. Therefore, this turbulence model seems to be

well suited for the current CFD application..

EAS Model. The Explicit Algebraic Stress

Model (EASM) proposed in Wallin and Johansson

(2000) provides an alternative to linear eddy

viscosity models (such as the SST k-ω) based on the

Boussinesq hypothesis. Often, linear eddy viscosity

models fail to offer satisfactory predictions for

complex three-dimensional flows, due to the

involvement of the Boussinesq assumption. This

leads to nonlinear stress-strain relations in

turbulence modelling that contradict the Boussinesq

assumption. (Gatski and Speziale, 1993).

Nevertheless, owing to their high level of stability,

these linear eddy viscosity models are commonly

used in the industry (Versteeg and Malalasekera,

2007).

The original algebraic stress model (ASM)

model is not often used as a result of robustness

issues and frequent instances of singular behaviour

(Deng, Queutey, and Visonneau, 2005), both of

which the EAS Model addresses by suggesting

treatment of the non-linear term by the production-

to-dissipation rate ratio, and the number of tensor

bases used to represent the explicit solution of those

equations. Gatski and Speziale (Gatski and Speziale,

1993) have identified an exact solution for three-

dimensional flow involving a ten-term tensor, but

require too much computational power. Alternatives

discerns that five terms yields acceptable

approximation of the solution to the algebraic stress

equation (Deng, Queutey, and Visonneau, 2005).

2.3 The Volume of Fluid Method, VOF

The VOF method is a multiphase flow method that

computes the interaction of several fluids or phases

of a fluid present in the same domain, and obtains

the interface between these fluids (Marek,

Aniszewski and Boguslawski, 2008). For the

purposes of yachting applications, implementation

of this method allows for the accurate inclusion of

the computation of the free water surface around the

hull of the yacht.

The VOF method calls for the solving of, the

same Navier-Stokes equation as do single-phase

flows. The difference lies in a phase indicating

function γ (Hirt and Nichols, 1979). This phase,

called the colour function or volume fraction,

displays the measure of the mixture of phases in

each cell. For instance, if γ = 1, the cell is

completely occupied by phase one, and if γ = 0.3,

30% of phase one and 70% of phase two are present

in the cell. In terms of yachting applications, the two

present fluids are water and air. As air is included in

this method, the spatial discretization must extend

above the waterline as well. This does, of course,

increase the computational effort of the simulation,

but it offers a significantly more accurate physical

representation of the waves, as will be explained

below.

The physical fluid properties used in the Navier-

Stokes equation for a multiphase flow is a blend of

the properties of the present fluids. In the case of

yachting, in which the present fluids are air and

water, the computational properties are blended in

the following manner:

To track the motion of the interface, a separate

transport equation for the colour function is used:

This method does, however, give rise to a

numerical problem regarding the smearing of

boundaries between the phases over several cells.

This smearing denotes that the water surface is

constituted by a gradual change in density between

water and air. As the water surface is a discontinuity,

a jump in density, this smearing represents an

unwanted phenomenon. It is a result of the

convective averaging being conducted across the

water surface. The remedy for this smearing is to

implement, in the code, a way to detect the presence

of a boundary (Hirt and Nichols, 1998) and treat the

bounded areas separately. In the Shipflow software,

the smearing problem is addressed by

implementation of a compressive discretization

scheme, as suggested by Orych, Larsson and

Regnstrom (2010).

To render visible the surface of the water, the

distribution of the colour function is evaluated.

Where 0<γ<1 there is a mixture between the fluids

and the free water surface is found. As mentioned,

however, the boundary between the phases may be

smeared, and therefore a specific value of γ is

selected to display the surface.

The VOF method belongs to the class of surface

capturing methods. In such methods, the interface

between two fluids is computed somewhere inside

the domain. The main difference from single-phase

surface tracking methods is that, in this case, the

dynamics of the air are also computed. In single-

phase methods, the water surface geometry forms

the top boundary of the domain, and thus these

icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport

194

methods do not take the air into account. The

geometry of the top of the domain is then in every

time step or iteration updated according to the

kinematic and dynamic free surface conditions, and

a new grid with new top geometry is generated for

the next iteration (Lasson and Raven, 2010). In the

VOF method, the free surface conditions are

automatically satisfied. Furthermore, surface

capturing methods have the advantage of being able

to capture overturning waves, drops and complex

surface features, if the resolution of the grid is fine

enough.

For the purposes of this paper, the advantages of

the VOF method in the form of physical

representation outweigh the disadvantages of

computational cost and numerical instability, and the

VOF method will therefore be used for all resistance

computations.

3 NUMERICAL METHOD

3.1 Description of the Computational

Domain

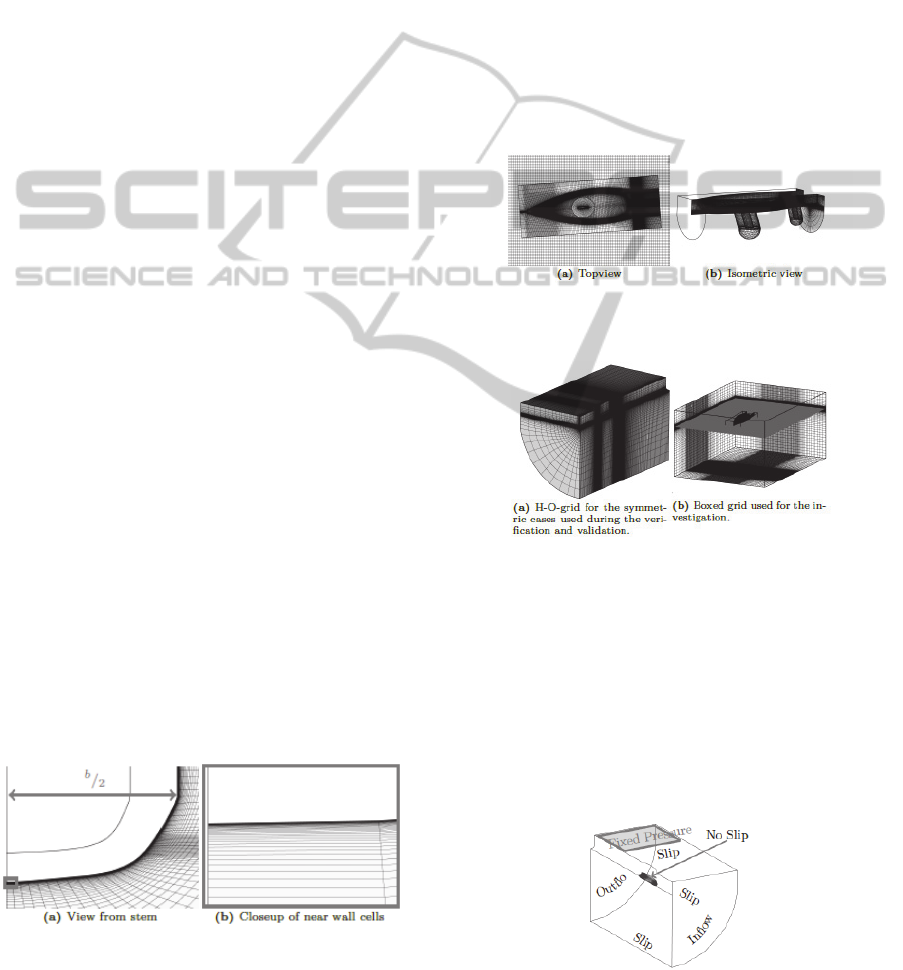
A structured H-O-grid defines the domain around

the hull. This grid layout is desirable because it will

generate cells that are roughly aligned with the

direction of the flow and fitted to the geometry.

Three different structured grids—the H-O-grid,

H-H-grid and O-O-grid—are used to cover each part

of the domain. The grid type refers to the shape of

the overall domain. The first two grid layouts are

displayed in Figures 5a and 5b, respectively. The

dome-shaped O-O-grid, used around the

appendages, is illustrated by Figure 4b.

The near-wall cells must be quite thin to allow

for representation of the velocity profile in the

boundary layer, as the gradient of the velocity

profile defines the amount of viscous resistance. No

wall function was used. The near-wall cells

distribution can be observed in Figure 3.

Figure 3: Display of cell density near the walled boundary

of the hull.

The H-O-grid layout is used, as displayed in Figure

5a, only in the verification and validation phase, as

the hull is then oriented straight against the flow,

which means that the case is symmetric. In these

cases, the simulations are also symmetric along the

centerline.

The H-H-grid, also called box, is used as the

main structure for the simulations of the heel and

trim variations. Figure 5b demonstrates this grid

layout. The geometrical representation of the

dinghy’s hull and appendages was then added to the

domain in the form of overlapping component grids.

When these component grids were added, they were

also given the selected angles of heel and trim

corresponding to the ones obtained at speed during

the towing tank tests.

Figure 4: Display of the subgrids used for the investigation

cases with appendages and leeway.

Figure 5: Overview of grid types.

3.2 Boundary Conditions

The boundary conditions for the domain are

displayed in the following figure. The slip boundary

condition is in practice the same as symmetric,

which is why the symmetry boundary is also marked

slip. The space above and behind the dinghy is also

discretized in two separate grid blocks which are

removed from the figure for better visibility.

Figure 6: Boundary conditions for the symmetric domain.

The same boundary definition is valid for the boxed grid.

CFDPredictionoftheEffectofAppendagesandLeewayontheForceTrendofanOlympicClassLaserDinghyHull

195

4 VERIFICATION METHOD

As the governing equations are implemented in a

computer code, the fields of the flow properties must

be discretized into smaller fluid particles to which

the equations are then applied. The differential

equations must be linearized and schemes must be

applied in order to estimate the derivatives. The size

of the cells in the domain impacts the flow’s

representation. In general, the smaller the cells, or

the larger the amount of cells in the domain, the

better the representation of the flow field (Versteeg

and Malalasekera, 2007). The number of cells will

influence to a great degree just how computationally

demanding the simulation will be.

The flow properties are stored in the center of

each cell. The cells interact, however, by way of

their adjoining boundaries, which means that the

quantities must be interpolated to the boundary from

the centers. This is done according to an

interpolation scheme implemented in the code. To

determine how well the interpolation scheme is

performing in terms of accuracy, a Taylor expansion

of a convective term (a derivative) is conducted

(Versteeg and Malalasekera, 2007). When the low

order terms are cancelled, the one left with the

lowest degree of dependency on the cell size defines

the scheme’s order of accuracy. The higher order

terms in the Taylor series are neglected and the sum

is truncated so as to only contain the one defining

term.

However, the theoretical order of accuracy, or

the decrease in error, might not be observed when

refining the grid. This may be attributable to the fact

that the refinement of the grid is not completely

uniform, to the fact that the wall distance necessary

for a turbulence model to be activated is not scaled

correctly, or to the fact that the aspect ratio of the

cells may change. One further explanation for the

inability to obtain the theoretical order of accuracy is

that the truncated higher order terms in the Taylor

expansion are in fact important for representing the

behaviour of the decrease in error.

Any difference between the real flow case and

the simulated case in any given quantity is called an

error. These errors can be subdivided into two

categories: physical modelling errors and numerical

modelling errors. Physical modelling errors originate

from a faulty model of the physical phenomena at

hand, for example, the use of inadequate equations

to describe the current phenomena. By contrast,

numerical modelling errors derive from the

procedures used to solve the equations in the

computer. Such errors might include the incorrect

rounding off of numbers, incomplete convergence,

insufficient spatial discretization, or a diffusive

discretization scheme (Larsson and Raven, 2010).

To ensure the trustworthiness of the CFD

simulation, the expected error must be quantified

(Roy, 2003). Here the quantification of the spatial

discretization error will be explained. The other

numerical modelling errors are excluded from the

verification study; this is possible if the grid

refinement factor r is greater than 1.1 (Slater, 2005).

In a validation study, the results of the simulation

are compared to the data from tests, rendering

indistinguishable the physical errors and the

modelling errors.

The verification procedure, called a grid

dependence study, aims to observe how a chosen

variable, called S, changes according to change in

the spatial discretization. In this study, the variable

will be the total resistance force of the dinghy. The

resistance force will then be plotted as a function of

the cell size h for each grid refinement. The data

points collected from the simulations of the different

grids will then be curve fitted to a certain function

and extrapolated to display a hypothetical zero cell

size case.

Furthermore, the verification study also offers an

accurate view of which errors can be expected as

computational effort inevitably increases and the

grid becomes more refined. The method for

extrapolation consists of an application of the

generalized Richardson extrapolation, called least

square root method (LSR).

4.1 Richardson Extrapolation

The equation for the Richardson extrapolation is:

The three unknowns require the use of three

different grids. The three solutions form a nonlinear

system of equations that have an analytic solution

(Roy, 2003) in which r denotes the constant grid

refinement factor r = h

i+1

and ε

= S

– S

4.2 The LSR Method

The drawback of the Richardson interpolation is that

it can only be used when the solutions are in the

asymptotic range of convergence, which means that

icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport

196

the cell size must be sufficiently small so as to

render the higher order terms insignificant (this

criterion can be quantified in two ways (Roache,

1998)). This in turn requires that the grids are very

fine in order to achieve the asymptotic range (Eca

and Hoekstra, 2014). The large computational effort

required made the LSR unsuitable for this study (the

method for dealing with the scatter of grids

considered too coarse for the explained method is

proposed in by Eca and Hoekstra, (2014)). The three

coefficients to equation 6 are then found by

minimizing the following expression:

Where ng is the number of grids used. When

using this method, more than three grids are required

in order to account for the scatter. This study used

seven grids.

4.3 Uncertainty

As the Navier-Stokes equations are not directly

solved, numerical models are applied to the

simulation. In doing so, not only is the error based

on the difference with respect to the test results of

interest, but the uncertainty of the simulation itself

becomes significant as well (Zou and Larsson,

2010). This uncertainty refers to the interval in

which the exact solution is expected to be found.

The purpose of the LSR method is to include the

exact solution within the error band with 95%

confidence (Eca and Hoekstra, 2006). The

appropriate method, an empirical one, is made and

adjusted to fit the test results presented at the

workshop of Eca and Hoekstra (2006) in a paper of

theirs (2014). The computation of uncertainty with

the LSR method is governed by the observed order

of accuracy p

, in the following manner:

Where:

1. The 





and the 





are obtained from curve

fitting the following functions in the same

manner as is described in section 4.2.

2. The 



Where the ∆ is the maximum data range,

max(|S

- S

3. The U

, 





and 





are the standard

deviations of the curve fitted functions: 6, 16

and 17, the standard deviation is found by

minimizing the following expression:

5 SYSTEMATIC VARIATION OF

NUMERICAL PARAMETERS

5.1 Numerical Parameter Study

From the first simulations of this study the resistance

was predicted to ~7% below the test data, which was

not satisfactory. In order to figure out how to

improve the result, the parameters of fluid density

ratio, height of domain, turbulence models and local

grid refinement were systematically investigated.

The outcome of these studies will be presented in

this section.

5.1.1 Fluid Density Ratio

This investigation was considered valuable for this

study as the default density ratio in the software was

set to a nonphysical value. The motivation for using

a nonphysical value was that the simulations become

more numerically stable for values closer to one,

which means two fluids of the same properties. The

result of this investigation can be seen in the

following figure:

CFDPredictionoftheEffectofAppendagesandLeewayontheForceTrendofanOlympicClassLaserDinghyHull

197

Figure 7: Result of density ratio investigation. The default

value in Shipflow was set to 0.01. The percent decrease

from 0.0013 to 0.01 is 0.90%.

Notice in Figure 7 that the trend is diverging as

the density ratio decreases and goes toward a value

of the physical density ratio of 0.0013. No results

from values below 0.0013 are reported because these

simulations did not converge.

The difference of 0.90% decrease from 0.0013 to

0.01 is not considered insignificant. However, as the

results in the region of low density ratio are

diverging rapidly, these results are not trustworthy

and this quantification shall be viewed with caution.

5.1.2 Domain Height

This investigation was done in order to see the effect

of the height of the domain on the resistance but also

the free water surface geometry in the transom area.

Water on the transom was appearing in the

simulations even though the transom evidently was

clear during the towing tank tests. The height of the

domain here refers to the height of the volume above

the water surface, occupied by air.

The number of cells in the z direction was kept

constant when the domain height was changed. The

results of this investigation can be seen in the

following figure:

Figure 8: Result of domain height investigation, domain

height refers to the height above the static water surface.

Default value in Shipflow was set to 0.5.

Notice in figure 8 that the resulting force increases

rapidly until 0.375 L

. The result from the

investigation shows a decrease by 2.27% from 0.563

to 0.125, with a plateau starting 0.375 L

. Domain

heights over 0.563 L

gave diverging simulations.

5.1.3 Turbulence Models

The selected software Shipflow implements two

turbulence models: SST k-ω and EASM, see section

2.2.2. As the different turbulence models give good

results for different types of flows, both of these

were tested in the validation case. The results are

presented in table 1.

Table 1: Grid dependency points data.

Concluded from this investigation is that the SST

k-ω model is the superior one for this case. The

EASM did not only predict a too-low total

resistance, it also took a lot longer to converge. The

medium-density grid with the EASM converged

with an oscillating trend, and a mean value over

2000 iterations had to be selected. This interval

represented roughly two periods of the oscillating

behaviour. The SST k-ω was then used for the

forthcoming simulations.

5.1.4 Cell Density in the Transom Region

This investigation also originated in having water

creeping up on the vertical transom of the dinghy.

The cause of this water was thought to be an

insufficient resolution of the grid at the corner where

the transom meets the bottom of the hull.

A consequence of refining the grid locally in the

transom area is the grid density at midships.

Stretching functions are used in the meshing tool of

the software, which makes the very fine cells

gradually grow larger with a certain factor. This

makes the cells at midships rather large as a limited

number of cells is used to cover the length between

perpendiculars. This could have been avoided by

adding more cells in this area, but as the transom

was the area of interest in this investigation this was

not done. The longitudinal direction was selected for

refinement. The results of this investigation can be

seen in table2.

icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport

198

Table 2: Result of the transom grid refinement

investigation. The cell density is in the longitudinal

direction, in the region aft of the transom.

The conclusion of the grid refinement was that

the transom water could be reduced by refining the

transom grid, but it could not be totally cleared.

However, the sought gain in resistance was almost

negligible and the cost for resolving the flow was

significantly increased. This concluded that the

transom grid was not the major cause of the too-low

predicted total resistance.

5.2 Result of the Verification

After selecting the best settings from the numerical

parameter studies, the following verification was

obtained (as shown in figure 9 and table 3):

Figure 9: Grid convergence plot. Gray line = curve fit

obtained order of accuracy; 1.75. Obtained S0 = 31.24N.

Black line = test data; 31.1N.

Evident in this grid-dependence study is that there is

a strong grid dependency. This means that a

substantial increase in grid definition should be able

to eliminate the ~7% error. The problem associated

with a further increase is the lack of memory on the

machines used to run the simulation during this

study. The limit for the available 24GB seemed to be

around 14.5 million cells.

Table 3: Grid dependency points data.

A further refinement of r equal to the 4

root of 2

would result in ~20.3 million cells, but a higher

refinement factor is probably needed as there is no

improvement observed for the finest presented grid.

The conclusion of the grid dependence study is

that the grid setup from grid 2 shall be used. To

decide which grid refinement results in a reasonable

error, the result is weighed against the computation

time. As grid 2 gave the best results and did not have

the highest computation time, it was selected.

Grid dependency for an appendage and leeway

case was not done, as the grid settings for the boxed

grid, required to include leeway, were not

successfully changed. This was due to lack of

knowledge in the meshing tool, which led to an

inability to systematically refine the grid.

6 VALIDATION RESULTS AND

DISCUSSION

The main investigation of the paper was to see if the

minima in resistance could be predicted at the same

angles of heel and trim, using the following

methods: bare-hull towing tank tests, bare-hull

simulations and simulations with appendages and

leeway. If this is the case, the more time-consuming

asymmetrical simulations needed for handling the

leeway can be rejected for future investigations of

this kind. The leeway simulations with the

appendages are interesting because they represent

real sailing conditions in the most accurate way

possible in a steady state setup.

The cases that are included in this study are heel

variation for zero trim and the trim variation for zero

heel. To find a global minima in resistance

combinations of heel and trim have to be simulated

as well.

A full series of simulations of heel and trim

variation was not completed. This was thought to be

due to a lack of knowledge in the software, that it is

still a young application of the VOF method and that

CFDPredictionoftheEffectofAppendagesandLeewayontheForceTrendofanOlympicClassLaserDinghyHull

199

it is usually handles ships of a very different kind.

The results of the simulations that are finished are

shown in the following section.

6.1 Heel Variation

The results of the systematic heel variations are

presented in figure 10.

Figure 10: Results of the heel variation. Black = test data,

Gray = bare hull simulations, White = Appendages and

leeway simulations.

The bare-hull simulations that are finished, and

shall be validated against the towing tank test data,

are still predicting very low resistance. This is

despite the use of the selected numerical parameters

from the variation study.

Concluded from the available results from the

four-knots-heel variation for the bare-hull cases is

that the error is larger than the error obtained in the

verification study. The best grid density was then

found to be one containing 4.3 million cells and the

settings for this grid would now be used for all the

simulations during the investigation. The exact grid

settings, however, could not be used, as the grid

layout will be changed. The grid layout used in the

verification study was H-O-grids, explained in

section 3.1. For the investigation part, however, the

boxed and overlapping grid was used. The reason for

this was that the simulations including leeway could

not be done in the H-O-grid. The bare-hull

simulations were also computed using the boxed

grid during the investigation to eliminate the effect

of different grid types on a comparison.

The setup of the boxed grid with the selected

settings was not done successfully. The reason for

this was a lack of knowledge in the meshing tool of

the software. A default setting had to be used

instead, which prevented the specific settings used in

the verification study to be applied.

The default grid settings led to a grid of 7.6

million cells. Recall that this setup is no longer

symmetrical through the centreline, and this would

therefore have corresponded to 3.8 million in the

verification case (where a grid of 4.3 million cells

was preferred). As can be seen in the depiction of

the 4 kts case the bare-hull simulations are some

~20% below the test data. Evaluating the results of

the verification the following fact can be observed;

first, a 20% error would have been predicted for a

grid of only 1.6 million cells, and then for a grid of

3.8 million cells an error of 12.1% could have been

anticipated. This mismatch between results is a

consequence of not being able to use the selected

grid settings. This also means that the errors of any

simulation with the default grid settings cannot be

estimated by the current grid dependence study. The

used cell densities are displayed in table 4.

Table 4: Comparison of cell densities at different regions.

Densities are expressed in cells per Lpp, y is expressed in

the dimensionless length unit.

This means that there are no means of evaluating

the error in these simulations. As there is no

complete series of heel variation, the trends of these

series are not available either, all indicating the need

for further research.

6.2 Trim Variation

The same goes for the trim variations; there are not

enough finished simulations to draw any conclusion.

7 CONCLUDING REMARKS

7.1 Systematic Variation of Numerical

Parameters

This section will sum up the study of systematic

variation of numerical parameters. The study

included four different parameters that were

expected to have an impact on the predicted

resistance of the simulations. These simulations

were conducted on grids of 4.5 to 6.5 million cells,

which turned out to be somewhere at the ~7%

plateau.

Density ratio. The result of this study was that

icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport

200

the most favorable density ratio was 0.01. The

resistance, however, could be increased by 0.90% by

using the physical density ratio, but as this led to

very numerically unstable simulations this was not

prioritized.

The conclusion of this investigation was that the

results seem to reach a plateau at 0.005 and the fact

that a higher density ratio really did make the

simulations more stable. Also, as only a small

increase in resistance was observed, it was decided

to continue the thesis work with the density ratio set

to 0.01.

Domain height. The domain height had a

significant effect on the resistance but also affected

the numerical stability of the simulation. Changing

the domain height from 0.563 to 0.125 L

resulted

in a decrease of 2.27%. Above 0.536 the simulations

became too numerically unstable. As the domain

height was ~0.5 L

in the previous simulations

already, and the threshold of domain height seemed

to be 0.536, the positive effect of increased domain

height could not be further exploited. The domain

height was therefore kept at 0.5 L

Concluded from this investigation was that the

domain height shall be set to 0.5 L

, or in this

particular case 2 meters, in order to still be in the

region of numerical stability but also to give a

resistance as close to the towing tank test result as

possible.

Turbulence models. The turbulence models that

were implemented for the VOF method in the

Shipflow software were EASM and SST k-ω. The

previously used SST k-ω was clearly superior to the

EASM in this case. As the EASM predicted a twice-

as-large error and took substantially more time to

converge, the SST k-ω was selected.

Cell density in the transom region. The

transom region was refined from the previously used

600 cells per L

, to 60’000. Only a slight increase in

resistance, 0.51%, was noticed. This study could

benefit, however, from more thorough investigation,

as it was discovered that cell density in other areas

of the hull was greatly affected by the transom area.

What can be concluded is that an insufficient

resolution in the transom area alone is not a major

source of error.

Some of the cases run during the main

investigation of this study converged to an

oscillating behaviour. This can be due to the fact that

the flow is not steady state after all. If the flow is

unsteady in the transom region, it can result in that

the steady state simulation gives this transom water

as a result. To test if the flow is unsteady, a transient

simulation has to be done, but as the selected

software did not have this option, this was not

investigated.

Another way of obtaining an unsteady flow in

the simulation is if the waves are not small enough

when they are leaving the domain. The remedy for

this will then be to increase the overall size of the

domain in order for the waves to naturally dampen

before reaching the boundaries.

7.2 Investigation

Though no conclusion can be made regarding where

the major source of this ~7% error lies, at least some

numerical parameters can be ruled out by this study,

facilitating further studies in the area.

The study presented in Chapter 5 took most of

the time devoted to this project. As no source for the

error was found during this study, the thesis work

moved on with a modelling setup that was not

accurate. As the objective of this paper is to find a

minima point of a series of heel and trim variations

and not necessarily an absolute value, it was still

considered possible. The setting selected during this

study was to be used in the investigation to the

largest possible extent. All grid density settings were

not to be kept completely similar, as the

investigation would be performed with the boxed

grid setup explained in section 3.1.

As explained in section 5.2, keeping similar grid

settings was not possible at all. The even-keel bare-

hull case was included in the heel and trim variations

but resulted in an even lower resistance than during

the verification. As there were larger errors than

expected by the grid dependence study, the

importance of a good grid became even more

evident. However, as the error for the verification

case increased so dramatically during the

investigation, it can also be concluded that the boxed

grid does not perform equally well in this case. This

conclusion can be made as the verification case was

tested with a non-symmetric H-O-grid as well. The

resistance was then 6.9% less than the towing tank

test run, compared to the 7.6% of the symmetric

case.

To be able to make decisive conclusions, further

investigation needs to be conducted. First of all,

decide if the VOF method should be used, and then

complete the heel and trim variations. The potential

flow method implemented in the software was tested

after this study, on the verification case, and

predicted the resistance within half a percent.

Here follows a list of suggestions for interesting

future research:

Simulate the full test matrix. To see get the

CFDPredictionoftheEffectofAppendagesandLeewayontheForceTrendofanOlympicClassLaserDinghyHull

201

global minima in resistance.

Provide sailing recommendations. Evaluate the

results of the heel and trim variations and make an

instruction of how to achieve highest velocity made

good, including a VPP study.

Investigate actual velocities and attitudes.

Study the sailors to see which velocities and

attitudes are common, to see if there is room for

improvement.

Tailor for individual crew weights. To really

maximize the effect of the individual sailor, a

separate investigation for the weight of the

individual sailor could be performed.

ACKNOWLEDGEMENTS

The authors would like to express their gratitude to

Professor Lars Larsson, Chalmers University of

Technology, Michal Orych, Flowtech International

and Matz Brown, SSPA Sweden AB, for their

contributions to this paper. Further we acknowledge

the financial support provided by Västra

Götalandsregionen, Regionutvecklings-nämnden.

REFERENCES

Davidsson, L., 2003. An Introduction to Turbulence

Models. Chalmers University of technology,

Göteborg.

Deng, Queutey, and Visonneau, 2005. Three dimensional

Flow Computation with Reynolds Stress and

Algebraic Stress Models. Engineering Turbulence

Modelling and Experiments (6), pp: 389-398.

Eca and Hoekstra, 2006. Discretization Uncertainty

Estimation Based on a Least SquaresVersion of the

Grid Convergence Index. In: 2

Workshop on CFD

Uncertainty Analysis; Lisabon; October 2006.

Eca and Hoekstra, 2014. A procedure for the estimation of

the numerical uncertainty of CFD calculations based

on grid renement studies. Journal of Computational

Physics 262, pp: 104-130.

Feymark, A., 2013. A Large Eddy Simulation Based Fluid-

Structure Interaction Methodology with Application in

Hydroelasticity. PhD thesis. Chalmers, Göteborg.

Gatski and Speziale, 1993. On explicit algebraic stress

models for complex turbulent fows. Journal of Fluid

Mechanics (254), pp. 59-78.

Hirt, C. W. and Nichols, B-D., 1979. Volume of Fluid

(VOF) Method for the Dynamics of Free Boundaries.

Los Alamos Scientific Laboratory, New Mexico.

Hirt and Nichols, 1998. Volume of Fluid (VOF) Method

for the Dynamics of Free Boundaries. Journal of

Computaional Physics (39), pp: 201-225.

Larsson and Raven, 2010. Ship Resistance and Flow. The

Society of Naval Architects and Marine Engineers.

Marek, Aniszewski and Boguslawski, 2008. Simplified

Volume of Fluid Method (SVOF) for Two-Phase

Flows. Czestochowa University of Technology,

Poland.

Menter, F. R., 1994. Two-equation eddy-viscosity

turbulence models for engineering applications. AIAA

Journal, Vol. 32, No. 8, pp: 1598-1605.

Orych, Larsson, and Regnstrom, 2010. Adaptive

overlapping grid techniques and spatial discretization

schemes for increasing surface sharpness and

numerical accuracy in free surface capturing methods.

Symposium on Naval Hydrodynamics, Pasadena

California, pp: 389-398.

Roache, P., 1998. Verication and Validation in

Computational Science and Engineering. Hermosa

Publishers.

Roy, C., 2003. Grid Convergence Error Analysis for

Mixed-Order Numerical Schemes. The American

Institute of Aeronautics and Astronautics (41), pp:

596-604.

Rumsey, C., 2013. The Menter Shear Stress Transport

Turbulence Model. Web Article.

url: http://turbmodels.larc.nasa.gov/sst.html.

Slater, J. W., 2005. Examining Spatial Grid Convergence.

Web Article. 2005.

url: http://grc.nasa.gov/WWW/wind/valid/tutorial/

spatconv.html.

Versteeg and Malalasekera, 2007. An Introduction.

to Computational Fluid Dynamics: The Finite Volume

Method (2nd Edition). Prentice Hall.

Wallin, S. and Johansson, A. V., 2000. An Explicit

Algebraic Reynolds Stress Model for Incompressible

and Compressible Turbulent Flows. Fluid Mechanics,

Vol. 403, pp: 89-132.

Zou and Larsson, 2010. A Verication and Validation Study

Based on Resistance Submissions. In: Numerical Ship

Hydrodynamics 2010. Workshop, pp: 203-254.

icSPORTS2014-InternationalCongressonSportSciencesResearchandTechnologySupport

202