
A Relation-Algebra Language to Specify Declarative Business Rules
Lex Wedemeijer
Department of Computer Science, Open University, The Netherlands, Valkenburgerweg 177, Heerlen, The Netherlands
Lex.Wedemeijer@ou.nl
Keywords: Declarative Business Rules, Relation Algebra, Modeling Language, Metamodeling, Rule Compliance.
Abstract: Business rules that apply within a business context must be formulated in a comprehensible way to allow
validation by their stakeholders, but at the same time they must be specified with enough precision to assure
their correct implementation in computer applications. These opposing demands of business rule modeling
are not easily reconciled. Formal rule modeling languages may be exact but they are often lacking in
understandability, whereas controlled natural languages are more easily understood but generally fall short
in exactness. We use Relation Algebra as the foundation to set up a controlled language for declarative
business rules that is compatible with practical demands, such as laid out in the Business Rules Manifesto.
Our version of controlled language comprises just five language statements that are orthogonal by design,
which makes for a language that is suited for use by novice business rule modelers. The language lets users
set up a business vocabulary that stakeholders can understand, and it allows to specify business rules about
the objects in the vocabulary in a comprehensible if-then syntax. Rules expressed in our language are
precise enough to permit the automatic generation of a prototype information system which is guaranteed to
comply with the rules. Stakeholders can explore this prototype to verify the vocabulary, and to check
whether the specified rules are valid and match their original intent of the business context. We show how
we can ascertain correctness of our language and metamodel, by adopting a reflective approach and subject
our context to rule analysis and specification, just like any other business context. It provides us with a
prototype system that lets us explore the rules about rules, and validate the rule compliance.
1 INTRODUCTION
Business rules play an important role in day-to-day
business operations and supportive IT applications.
Declarative rules restrict what states are permitted in
the business, and which operations may be executed
by employees and information systems of that busi-
ness (Hay, Healy 2000).
There is consensus that the business rules should
be validated by stakeholders in the organization to
ensure their overall correctness and coherence (Busi-
ness Rules Manifesto 2003). Therefore, rules must
be expressed in a way that a target business audience
clearly understands. But to use those very rules in
software applications calls for exact specifications
and computer precision. This poses contradictory de-
mands: comprehensibility for lay users, but perfect
exactness for programmers and applications.
The prime deliverable of rule-based design is a
compliant database application. In practice, the
informal rules of business behaviour are rephrased
and transformed in a chain of handovers until their
encapsulation in an enterprise information system
(figure 1). At each point in the chain, requirements
are translated into yet another language, a process
which is prone to misinterpretations, loss of detail,
and other problems, even in the presence of a valida-
ted vocabulary (Bajwa et al., 2011).
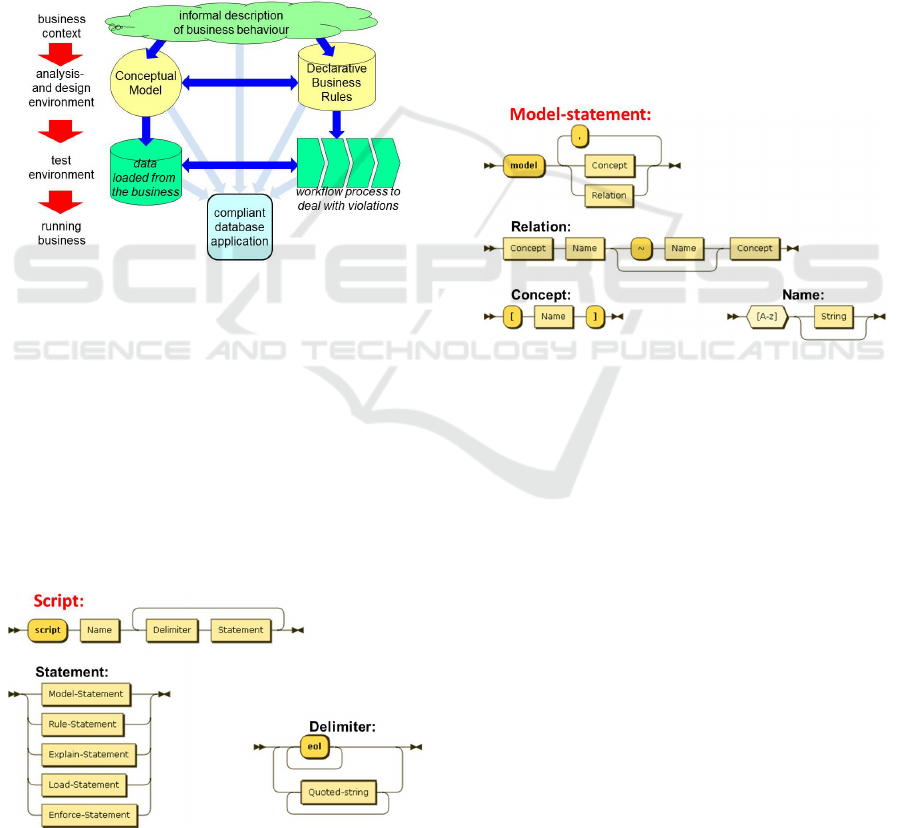
Figure 1: Chain of handovers of business rules.
To reduce the need for translation, we propose a
simple language founded on proven theory to cover
the major part, if not the entire chain of handovers.
The business rules considered in this paper are
declarative: there is no procedural dependence or
hidden sequencing. The rules are also invariant: they
concern persistent states only, not some transient
situations that exist for just a brief moment in time,
63
Wedemeijer L.
A Relation-Algebra Language to Specify Declarative Business Rules.
DOI: 10.5220/0005424400630073
In Proceedings of the Fourth International Symposium on Business Modeling and Software Design (BMSD 2014), pages 63-73
ISBN: 978-989-758-032-1
Copyright
c
2014 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

e.g. only while a data transaction lasts. This differs
from IT-approaches like the Event-Condition-Action
(Poulovassilis et al., 2003) paradigm, or
Communicating Sequential Processes (Hoare, 1985;
Wedemeijer, 2012). From a business point of view,
the ECA type of rules have a technical ring, and
their relevance is experienced as vague, difficult to
retrace, and hard to explain (Andreescu, Mircea
2014).
The paper outline is as follows. Section 2 dis-
cusses some contemporary languages for declarative
business rules, and design considerations for our lan-
guage. Section 3 describes the proposed language.
The syntax of each basic statement is depicted as a
railroad diagram, and we explain core ideas. Section
4 puts the language to work, by describing features
of supportive design- or prototype environments.
Such an environment can be regarded as a business
context having its invariant rules captured. In section
5 we pursue this idea by developing a meta-model of
the language. Section 6 presents conclusions.
2 RELATED WORK
Business rule languages must be comprehensible for
business workers on the one hand, and faultlessly
exact for computer applications on the other
(Bjekovic, Proper 2013). Numerous languages to
express declarative business rules exist (Kardasis,
Loucopoulos 2004). Our discussion of languages is
restricted due to lack of space.
2.1 Declarative Rule Languages
On one side of the spectrum of languages to express
business rules are natural and semi-controlled langu-
ages. Prominent Semantics of Business Vocabularies
and Rules (Object Management Group 2008). One
of its derivatives is RuleSpeak, 'a set of guidelines
for expressing business rules in concise, business-
friendly fashion using structured natural language'
(Ross, Lam 2011). Another derivative is Attempto
Controlled English (Fuchs et al., 2008).
These approaches rely on business vocabularies,
also called 'fact models', in order to capture the true
meanings and definitions of business data. Hence,
comprehensibility and business focus is a strong
point. However, controlled languages still permit a
large variety in phrasing, and lack uniformity. As a
result, rules are not always concisely and clearly
expressed, making validation difficult and leaving
room for interpretation, two fatal shortcomings for
IT implementation (Weigand et al., 2011).
Other standards based on SBVR are FBM (FBM
Working Group 2011) and Object-Role Modelling
(Halpin, 2011). Both standards depict conceptual
models in the customary way, and then depict the
constraints visually. As a result, the diagrams with
constraints become quite confusing, and they are
barely intelligible for lay users.
A middle field is languages that aim to describe
enterprise architectures, stakeholder concerns, goals
and business rules (Quartel et al., 2009). Generally,
these languages are not geared to capture rules, and
are too high-level to allow validation by business
stakeholders, or implementation in IT-systems.
On the other side of the spectrum are languages
with an IT-provenance, such as UML- and XML-
based languages or DTD's. Many of these languages
are 'rich', meaning that a business feature may be
captured in a variety of ways (Lamrani et al., 2013).
Hence, it requires a thorough knowledge of imple-
mentation details to disclose the business relevance
of an implemented rule (Beckner, 2014). Andreescu
and Mircea (2014) remark on the reluctance to use
OCL in the early design phases, when IT specialists
need to cooperate with business people.
RuleML is an evolving family of XML-based
languages (Boley et al., 2004). Semantic Web Rule
Language, SWRL for short, achieves an expressive
power superior to our language in some areas, e.g. to
specify derivations, numeric and time calculations
(Horrocks et al., 2004). SWRL also includes the
Horn-clause syntax for rules, a strong point that
which we will employ in our language. Nonetheless,
the IT-orientation and notational complexity of
SWRL, and XML-based languages in general, make
them unsuitable for an average business user or
novice designer (Akbari et al., 2103).
We conclude that (controlled) natural languages
may capture business rules in a comprehensible and
validatable manner, but not precise enough for
computer applications. Formal rule modeling
languages or general IT languages may be exact
enough, but they lack in understandability.
2.2 Language Considerations
With the above in mind, our language for business
rules was devised with the intention to:
ensure comprehensibility for business people by
relying on business vocabulary (terms and
phrases of the business context).
ensure that business workers can understand and
validate their rules, and so minimize the need for
back-and-forth translation of rules.
ensure orthogonality of the language, so that
Fourth International Symposium on Business Modeling and Software Design
64
features are always expressed in just one way,
and so avoid the problems of 'rich' languages.
ensure exactness of rules, by founding them on
rigorous mathematical theory; we opt for binary
Relation Algebra (Maddux, 2006).
To prevent trivial but cumbersome errors in data
entry, we prefer names and identifiers to be case-
insensitive. Also, leading and trailing spaces should
be avoided as much as possible.
2.3 Way of Working
Rule design may be conducted in a progressive way
of working (figure 2).
Figure 2: Way of working in rule-based systems design.
The approach starts at business behaviour, which
in most cases is only informally understood.
In the analysis and design phase, a business
model of concepts and relations is created capturing
the relevant parts of the business vocabulary. And,
very important, the declarative rules are captured.
In the test environment, data for concepts and
relations is loaded incrementally to test whether the
predicted rule violations emerge. Rule enforcements
are specified, determining how workflow processes
should deal with rule violations in practice.
Figure 3: Railroad diagram for script and statements.
3 PROPOSED LANGUAGE
Our language provides five statement types that a
designer may use in the specification of a business
context. A railroad diagram of the overall language
set-up is shown in figure 3.
Statements in a script may appear in arbitrary
order, to suit an incremental, step-by-step, top-down,
big-bang, modular, or any other preferred approach
of the designer. The statements are uniform in make-
up: first a reserved language imperative, identifying
name(s) next, and then the further particulars.
3.1 Model
The model statement defines the concepts and binary
relations that are part of the business vocabulary
(figure 4). It sets up the structure of concepts and
relations that the designer considers to be important.
Figure 4: Railroad diagram for the model statement.
Concepts have unique names, enclosed in square
brackets for clarity, and starting with a letter.
Relations are uniquely identified by a colloquial
name to call the relation by, plus the names of its
domain and range concepts. In addition to the
colloquial name for the relation itself, another name
may be provided for the inverse relation, indicated
by the ~ inversion symbol. Uniqueness requirements
for the relation name also apply to the inverse name.
We prefer the infix style of notation for relations.
It enhances readability and prompts designers to
pick self-explanatory relation names. Technically
speaking, prefix or other styles are equivalent.
A script may contain multiple model statements,
so that concepts and relations can be incrementally
introduced. And because concepts are easily dedu-
ced from relation domains and ranges, a designer
may even forego the explicit modelling of concepts.
By definition, it is impossible to violate a model.
All true facts observed in the business context, either
fit perfectly in the structure, or they are irrelevant. If
some business fact is relevant but still cannot be
A Relation-Algebra Language to Specify Declarative Business Rules
65

expressed as atoms or tuples, then the structure is
wrong: it is an inadequate model of the business
context. Thus, a model may be regarded as a set of
structural rules. As no other rules apply to it, we call
this an Unconstrained Conceptual Model.
3.2 Rule
We are now in a position to specify 'behavioural'
rules that business stakeholders ought to live by.
These rules should always evaluate to being satis-
fied, but in a running business, they may temporarily
be violated. The implication is not, that the model is
wrong. Rather, the business stakeholders should take
action to remedy the violations.
The combination of model and rule statements is
sufficient for business rule analysis and design. The
joint deliverable may be called a Conceptual Model,
and a good designer will make sure that it meets the
usual quality requirements, such as completeness,
and consistency of its rules (Moody, 2005).
To emphasize the behavioural aspect of rules, a
core position is given to the rule keyword 'must' in
the rule statement. The idea, in accordance with the
ideas of RuleSpeak (2014), is to help users grasp the
rule intent: guiding the business behaviour and have
people refrain from violating the rule.
Each rule comes with a unique rule identifier,
starting with a digit 0.9. Other statements can refer
to the rule by way of this identifier, and it also
comes in handy when violations are to be reported.
3.2.1 Simple Rules: Cardinality Constraints
A single relation may already be subject to a simple
rule, i.e. cardinality constraints may apply. For and
understandability, our language provides keywords
to express cardinalities and common combinations.
For instance, the keyword 'function' means that a
relation must be univalent and total. In addition, we
provided keywords for ruletypes of homogeneous
relations. And although simple ruletypes usually
apply to simple relations, a compound expression
may also be subjected to this kind of rule.
Combining disparate cardinalities under one
heading defies the idea of having a unique identifier
for each distinct rule. The designer should decide
whether or not to combine rules, depending on how
the user community understands these rules and
deals with possible violations.
Notice that simple ruletypes are syntactic sugar:
all simple constraints are perfectly expressible in
mathematically equivalent compound rules. We
include the rule keywords in our language for the
sake of simplicity. In practice, it makes little differ-
ence: a rule is referenced only through its identifier,
independent of the mathematical formulation.
Figure 5: Railroad diagram for the rule statement.
3.2.2 Compound Rules: If-then Phrases
The real benefit of Relation Algebra is found in its
ability to formulate compound rules in the concise
yet straightforward way of normalized Horn clause
format (Horrocks et al., 2004):
antecedent ⇒ consequent
Both the antecedent and consequent are binary
relations, either a plain relation of the Unconstrained
Conceptual Model or a compound expression, and
must have the same concepts for domain and range.
This format is easily translated to a semi-formal if-
then sentence (1), into which we like to include the
important rule keyword 'must':
IF the antecedent is confirmed,
THEN MUST the consequent be confirmed
(1)
We define a rule violation as: a pair in the ante-
cedent, but absent from the consequent expression.
With this definition, the text becomes:
IF a pair is present in the antecedent,
THEN MUST the pair be in the consequen
t
The Horn-clause format easily pronounces as 'if...
then must...', but the mathematical expressions in a
rule may be quite complex, as seen in the railroad
diagram of figure 5. Both expressions in the Horn
clause may be a relation of the Unconstrained
Conceptual Model, or may combine several relations
using unary and binary operations. Special relations
and constants may also be included, as explained
below. It requires skills and business knowledge to
translate the complex expressions into terms that the
user community can understand. Better still is to
Fourth International Symposium on Business Modeling and Software Design
66
avoid complex expressions altogether, and find easy-
to-explain, natural rule assertions to begin with.
3.2.3 Special Relations and Constants
Complex expressions in rules may call for special
relations. Our language provides a number of them,
such as entire Cartesian Product, the empty relation,
and the identity relation on a concept.
Expressions may also contain constant values or
literals. Such values act as atoms or tuples in the rule
expressions, but they need not be on record as they
do not necessarily represent true business facts.
Constant values in rules may force certain tuples to
be on record. For instance, the rule 'the president of
the USA must be a citizen', implicitly assumes that a
nation named 'USA' is recorded. If we eliminate the
constant by rephrasing the rule to 'the president of a
nation must be a citizen of that nation', then the em-
pty database no longer violates it. In general, an
empty database never violates a rule if no constants
are involved in the rule (Decker, Martinenghi 2006).
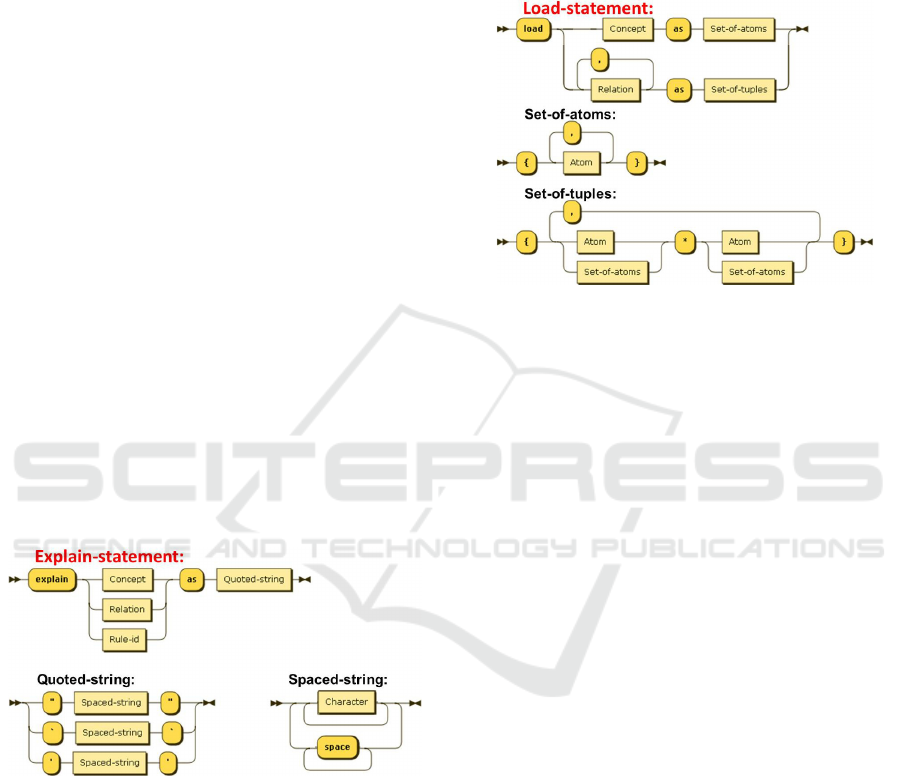
3.3 Explain
True business relevance means that each node, edge
and clause in the specifications, can be clearly ex-
plained for, to, or even by the business workers. To
help the audience grasp the detailed meaning and
structure, explanatory texts are helpful (figure 6).
Figure 6: Railroad diagram for the explain statement.
An explain statement addresses either a concept,
a relation, or a rule, each of which comes with its
unique identifier. The explanatory texts do not alter
the contents of the model or the rules and violations
and therefore any number of explain statements may
be given for a single concept, relation or rule. The
aim is to help users in understanding both the details
and the overall structure of the model.
3.4 Load
An important means to put a model and rules to the
test is by loading data and check for rule violations.
The ability to load data is also useful when a design
is demonstrated to the business stakeholders.
Figure 7: Railroad diagram for the load statement.
The load statement places sets of atoms, delimi-
ted by curly brackets { .. }, into a concept extension,
or sets of tuples in relation extensions (figure 7).
Loading of data is not obligatory, but if data is
loaded, then entity integrity and referential integrity
is required (Date, 1981). At design time however,
there is no need to worry about this, because it can
be automatically ensured at load- and runtime.
3.4.1 Specifying Data
Like concepts, the atoms in our language are self-
identifying: an atom is fully specified by its name,
which is merely a text string, plus (the name of) the
concept it belongs to. We do not distinguish between
atom, atom-name, atom-value, or identity, distinc-
tions that are hard to explain to lay users. Moreover,
the atoms and their distinguishing names, or id's, or
values must be linked tightly. Links that, on a meta-
level, prove to be isomorphisms, or almost so. We
think that such intricacies are better avoided.
Writing lots of data for loading is boring, and
prone to typing errors. Our language provides two
shortcuts. First, several relations may be loaded at
once, provided of course that the domain and range
are identical for all of them. Second, instead of
specifying one tuple at a time, a set of tuples can be
specified in one go, by combining a set of atoms
from the domain with a set of atoms of the range.
3.5 Enforce
Enforcement is how runtime violations of the rules
A Relation-Algebra Language to Specify Declarative Business Rules
67
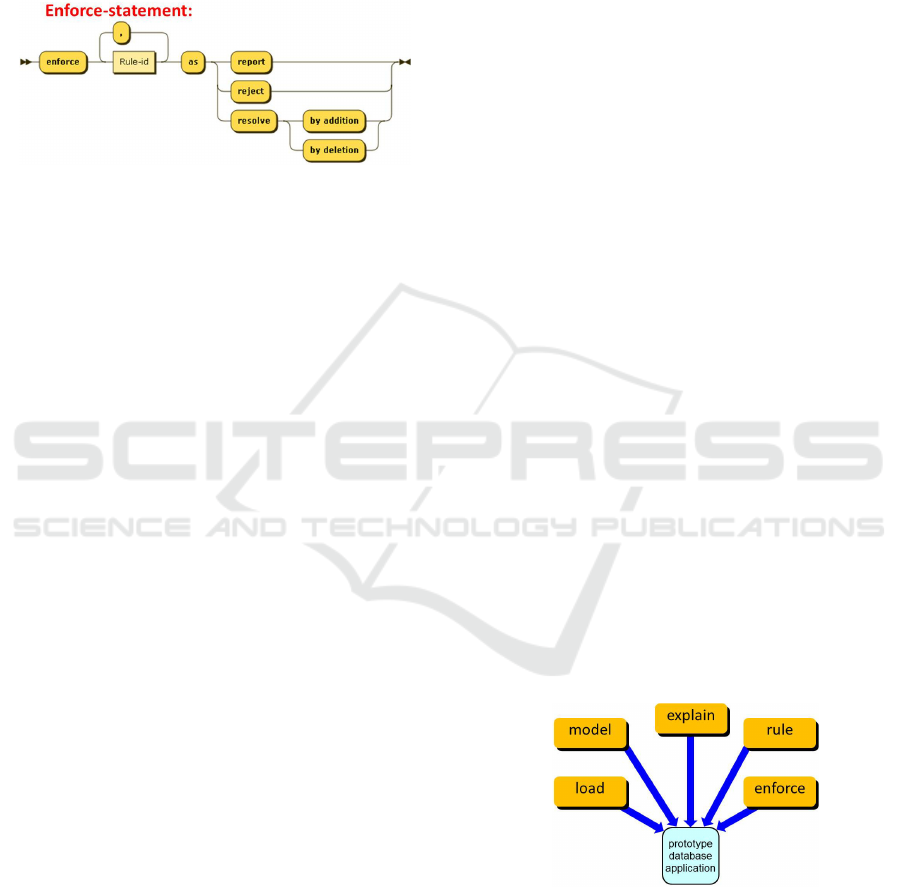
should be dealt with from the business point of view.
In realistic business environments, enforcement may
range from 'avoid violation at all cost' to 'comply or
explain' or even 'ignore all violations'. From the IT
perspective however, there are just three main
strategies called 'projector', 'rejector', and 'producer'
(Dietz, 2008).
Figure 8: Railroad diagram for the enforce statement.
Our language provides for variants for all three
variants. Figure 8 depicts the railroad diagram for
the enforce statement in our language.
Enforce is not an incremental statement: a rule is
subjected to one enforcement strategy at most, and
specifying multiple enforcements for one rule has no
use. If no enforcement option is specified for a rule,
then the 'report' strategy applies by default.
3.5.1 Report
We call 'report' what the literature is referred to as
'projector'. This strategy for a rule means that after
some edited data is committed, the rule is assessed,
meaning that all violations are 'projected' into a
special database table. Next, that listing is reported
to the stakeholders. Notice that all violations ought
to be reported, not just the new ones caused by the
latest data edit.
Generally speaking, the 'report' strategy is easy
to understand and robust to implement, which is why
it is the safe choice for any business rule. For this
reason too, this strategy is the default at load time.
3.5.2 Reject
The 'reject' type of enforcement strategy means that
the rule must be checked prior to committing a
change of data. If the change would result in a new
violation for this rule, then the change should be
rejected offhand, and the data not recorded.
The assumption underlying reject is that data
violating this particular rule cannot even be valid in
the business context. Rejection may be bothersome
for business workers because this assumption is
sometimes wrong, so that perfectly valid data is
rejected for a bad reason.
There is another loophole: data may actually be
in conflict with the rule, but if by coincidence the
violating tuple is already present for another reason,
then the erroneous data can be recorded nonetheless.
3.5.3 Resolve by
We introduce 'resolve' as final enforcement strategy
for rules, referred to in the literature as 'producer'.
The idea here is that sometimes in the business
context, there is only one viable way to resolve a
violation. And if the solution is known, why not let
the computer apply it automatically?
We recall our definition of violation as a pair in
the antecedent expression of a Horn clause, but not
in the consequent. Hence, adding the offending pair
into the consequent is a straightforward solution, and
this is exactly what the enforcement strategy 'resolve
by addition' intends. The strategy called 'resolve by
deletion' takes the opposite tack and bluntly deletes
the pair from the antecedent. As expressions in
general cannot be edited, a necessary restriction is
that the expression being edited must be a relation of
the Unconstrained Conceptual Model.
A data-edit transaction is produced and in fact,
this may result in the violation of some other rule.
The automatic transition may even be rejected by
another rule, or a subsequent transaction may be
produced, and so on, potentially creating deadlocks
or interminable loops. While compliant with the
theory of Relation Algebra, this strategy goes
beyond our context of invariant, i.e. state-oriented
business rules. In defining our language, we did not
investigate these effects nor have we tools for the
rule designer to control them.
4 LANGUAGE ENVIRONMENT
Figure 9: Contributing to the generated prototype.
The prime deliverable of rule design is a working
database application that assures rule compliancy.
Putting our rule language to work requires a design-
and runtime environment in which all five of our
statements contribute to that deliverable (figure 9).
As we strictly adhered to the sound theory of Rela-
Fourth International Symposium on Business Modeling and Software Design
68

tion Algebra, the generated prototype is guaranteed
to comply with the invariant rules in the script.
4.1 Design Time Interface
A design time interface should support a designer to
create, expand, refine and correct her script, and also
to save the script to continue work at a later time.
A graphic display of the Unconstrained Concep-
tual Model, with drag-and-drop and rearrange featu-
res to uncluttered the diagram, is a wonderful help in
composing and understanding. Still, it is the model,
the rule statements and explanations that should be
at the core of the design effort, not the diagram.
The rule statement calls for a smart formula
editor, with an option to link each rule expression to
corresponding nodes or edges in the model diagram.
Various flags would also be desirable, such as flags
for faulty expressions, rule inconsistencies, potential
simplifications of rules, or unconstrained relations.
The explain statement can well be supported by
providing text editing functions in a mouse-over of
the diagram.
The load statement needs generous support to let
a designer include a full load of initial data in the
script, and integrity should be taken care of
automatically, at load time at the latest. Copy and
paste of realistic data acquired from the business
arena would be greatly appreciated. Automatic
generation of datasets in compliance or violation of
a specific rule, would also be desirable.
Lastly, no special support appears to be required
for the enforce statement at design time.
4.2 Load Time Interface
At load time, all data in the script should be loaded
into the Unconstrained Conceptual Model. Only the
'report' enforcement strategy is feasible at this time,
to prevent undesired outcomes or even deadlocks
caused by 'reject' or 'resolve' types of enforcement.
But data integrity must be made to hold. Refe-
rential integrity holds that each tuple refers to atoms
on record in the domain and range, respectively. One
option is to apply 'cascading delete', i.e. ignore all
tuples that refer to a unrecorded atom. The opposite
option is more attractive, i.e. to automatically insert
the domain and range atoms of all tuples. Entity
integrity holds that duplicates of an atom or tuple
already on record, should not be loaded.
Once data is loaded into the Unconstrained
Conceptual Model, only then should the rules be
checked and violations reported. The report should
enable the designer to trace each violation: what rule
is violated, which atoms and tuples play a part.
A smart designer selects her data for loading in
such a way that each violation is clearly understood,
explained, and repaired. If a violation cannot be
understood, then either the loaded atoms and tuples
make no sense in the business, or the rule itself is in
doubt. Or if particular violations can only be
repaired by rigorously deleting data, then apparently
some rules are contradictory. In any case, business
people should be consulted to clarify the issue.
4.3 Runtime Interface
The script captures the rules of the business context,
and a computer interface serves to confront the
business community with their rules. Conveniently,
it makes little difference how a designer organizes
her statements in the script, because the business
users are not exposed to the script directly.
A minimal requirement is a browse-and-explain
interface. This should help users understand their
exact business rules and violations. It ought to depict
uncluttered diagrams of the entire Conceptual Model
or parts thereof. It should display relevant explanati-
ons for all the concepts, relations and rules in the
diagram. Also for each rule a complete list of all
persistent violations must be provided, with
explanations and traces how each violating tuple is
determined from the corresponding Horn-clause
formula. From there, the interface should support
drill-down features to scrutinize partial populations
or even individual instances in the diagrams.
Second, a demonstration interface is appreciated
to emulate a workflow case in a (partial) business
process. A series of predefined datasets is loaded in
sequence, showing the emergence and subsequent
resolution of violations as new data is being entered.
Adjusting rule enforcements on the fly in the
runtime interface is still better. This would allow
experimentation how to deal with rule violations and
to probe the effects on the workflow processing.
The real benefit of our language is to generate a
rule-compliant runtime prototype application with
full data edit capabilities. Business people can then
put that prototype to the question by entering all
conceivable kinds of business data, view the
responses by the system, and come to understand the
workflow processes for dealing with the violations
of their business rules.
5 LANGUAGE METAMODEL
So far, we discussed the modelling of an arbitrary
A Relation-Algebra Language to Specify Declarative Business Rules
69
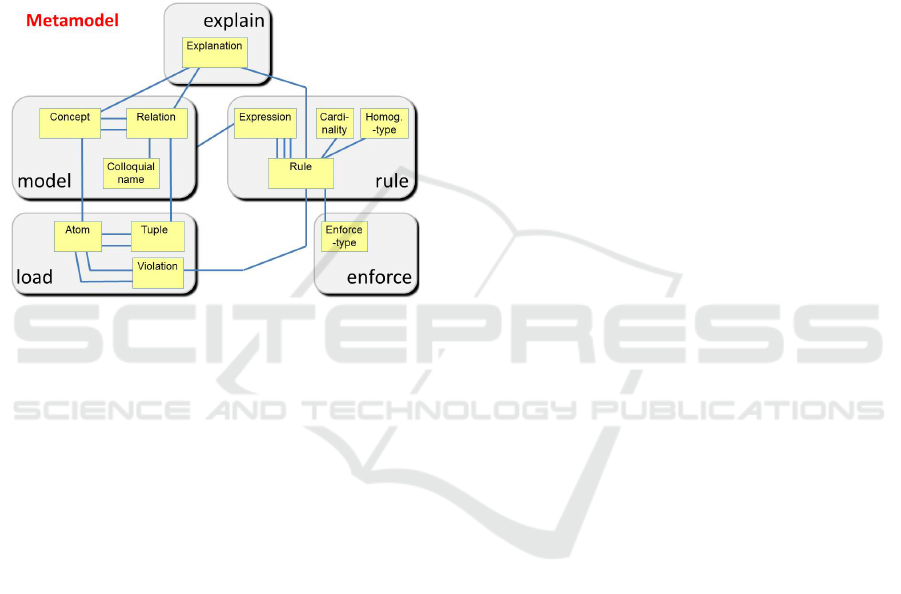
business context, its vocabulary and rules. In this
section, we change the perspective and select 'rule
design' for our business context.
5.1 Metamodel
What is the business vocabulary of design? What are
its rules? If we could specify this special context in
perfect detail, and if a compliant tool environment
would be available, then we could use these... to
generate the prototype system for rules design, in a
truly reflective approach.
Figure 10: Metamodel of the language (conjectured).
The idea, although not new (Schön, 1992), is still
worthwhile to pursue. Having outlined the relevant
business context in section 3, we present a conjectu-
red metamodel in figure 10. In the diagram, we use a
freehand style, and we omitted the meta-relation
names. Interestingly, the statements of our language
can be associated with five distinct areas in the
metamodel.
Evidently, the metamodel comes with its own set
of rules constraints on the metamodel concepts,
associations, and contents. Without being exhaustive
we outline some major rules per area.
5.2 Meta-rules and Enforcement
Entity integrity is an intrinsic demand of relation
algebra, and it applies in this metamodel as well.
Duplicate atoms of a concept or duplicate tuples in a
metamodel association are unacceptable at any time,
This integrity demand can be enforced as 'reject', in
other words: duplicate entries are simply ignored.
In the 'model' area, it is compulsory that each
relation has exactly one domain concept, one range
concept. Referential integrity proclaims that both
concepts must be present in the extension of the
Concept concept. This rule is easily enforced as
'resolve by addition', meaning that missing concept
names are automatically inserted. Moreover, the
domain concept, range concept, and colloquial name
together must uniquely identify the relation. And if a
relation's inverse name is given, then it must adhere
to the same uniqueness demand.
In the 'rule' area, a simple rule is associated with
one expression and one (or more) cardinality- or
homogeneous-ruletype. The compound rules, i.e.
those in Horn clause format, are associated with both
an antecedent and a consequent expression that must
have the same domain and range concepts.
Regarding the 'expression' concept, it must first be
noticed that any particular expression may well be
associated with several rules. Second, an expression
can involve many relations, or concepts, or even
constants, which is why we depict an non-specific
line from 'expression' to the 'model' area in the
metamodel diagram. Finally, it must be realized that
expressions in general will constitute derived
relations. That is, except in the special case where
the expression equals a relation defined in the
Unconstrained Conceptual Model.
In the 'explain' area, explanatory texts are
associated to concepts, relations and rules, but no
particular restrictions apply. In the 'enforce' area of
the metamodel, only a uniqueness restriction applies.
5.3 Example of a Meta-rule
In the 'load' area, referential integrity must again be
made to hold. As an example how analysis may be
conducted and how our language supports the rule
designer in her analysis, let us show how to capture
referential integrity in a rule enforcement.
Referential integrity holds that for any tuple in
any relation, both of its atoms must be on record:
IF the tuple T has the domain atom A,
THEN MUST that tuple T is contained-in
some relation R which has domain some
concept C which contains that atom A.
This controlled-language sentence translates to a
rule in our language as an Horn-clause implication,
with symbol ; indicating composition of relations:
rule 2-referential-integrity-domain as
[Tuple] has-domain [Atom] must imply
[Tuple] contained-in [Relation]
; [Relation] has-domain [Concept]
; [Concept] ~contained-in [Atom]
(2)
The antecedent expression is a relation in the
Unconstrained Conceptual Metamodel. Hence, this
rule assertion (2) permits us to impose the 'resolve
by deletion' enforcement strategy: any tuple refer-
Fourth International Symposium on Business Modeling and Software Design
70

ring to an unrecorded atom is immediately deleted.
This strategy is known as 'cascading delete' in
relational database technology. A similar meta-rule
will do for the atoms in the range of the relation.
The rule of integrity must hold at runtime, but
still its enforcement strategy can be made to vary. A
'reject' or 'report' strategy may be better in a running
business environment. Moreover, at load time the
'resolve by addition' strategy is to be preferred.
This illustrates how there are unresolved issues
in the analysis and design of the metamodel calling
for further research. Another issue is how to deal
with constant values in rule expressions.
6 CONCLUSIONS
We proposed a rule language to capture and express
declarative business rules. The language, combining
business vocabulary with precise mathematical
features, is comprehensible for business users, and
precise enough to generate rule-compliant IT appli-
cations. We outlined how the language may be
employed in design- and runtime interfaces.
6.1 Expressive Power of the Language
We claim that the language has adequate expressive
power for rule design and analysis.
Following the ideas of SBVR, our language is
founded on business vocabulary, compelling the
designer to use the plain business phrases for the
relevant terms and facts, a major strength of our
language. Declarative, invariant business rules are
described in a comprehensible if-then syntax. In our
experience, this is a great help for people reading a
script. In particular, the 'must' keyword provides an
immediate clue of what a rule intends to say, even
when complicated expressions are involved.
Our language has a clear, uniform makeup. This,
and the simple naming regime make for easy-to-read
scripts that are straightforward to interpret by
business people, even without supportive IT-tools.
Each line in a script starts with an imperative
keyword that clearly indicates the focus of that line,
underpinning the orthogonality of our language. The
reserved keywords of our language are concise and
learnable, appealing for both skilled business
workers and novice rule designers.
Statements of our language are orthogonal by
design. Each statement addresses a single aspect of
the business context. The language statements are
loosely coupled, but as some statements necessarily
depend upon previous ones, complete independence
is not possible.
No restrictions apply to the order or sequence of
statements. The designer may first specify all
aspects of one business feature, or start a model with
a few rules in one section of the script and add a
section with load statements later, etc. Therefore, no
particular design approach is forced upon the
designer. Having said that, a strong point of our
language is that it does force a designer to consider
all business features of the relevant rules, and to
capture its aspects in distinct statements. For
business users, it makes little difference how the
statements in the script are organized, because in
theory, users do not browse the script but use a
dedicated interface to explore the rule-based design.
In practice however, users will probably read it, and
even begin to add and amend the script.
Our statements are devoid of typical IT jargon
such as primary-keys and attributes, functional
dependencies, cascading deletes, etc. Imperative
ECA-type rules cannot be formulated in our
language, with one exception. The enforce statement
variant called 'resolve' does initiate data editing
operations in response to a rule violation. This is a
digression from the strictly declarative and invariant
nature of our language, the consequences of which
need to be further researched.
In our opinion, rule design for a business context
is a superior approach than the dual approach of
creating on the one hand an implementation data
model with objects, entities, keys, and an activity
model with data transitions and processing features
on the other. Business stakeholders have little
affinity with such refined IT-models, and lack the
ability to validate the correct implementation in
computer applications.
6.2 Language Extensions
Several extensions to the language may be
considered to enhance usability for stakeholders and
compliancy of the implementations. Of course,
expressive power and understandability for business
users should not be affected.
Support for specialization/generalization relati-
ons among concepts is one possible extension. This
is somewhat problematic for Relation Algebra
theory because an atom might belong to more than
one concept for some time, or even switch over
time: a person is student at one time, and teacher at
another. Specialization/generalization is relatively
unimportant in business practice, where models
often do not need it or can use a work-around.
Better support for the 'resolve' enforcement
A Relation-Algebra Language to Specify Declarative Business Rules
71

strategy is needed. Fundamental research is called
for to understand the coordination of rules, and to
prevent contradictory enforcement strategies.
Support for the Role-based Access standard
(Edward et al., 2011) is also suggested. Instances of
a Role concept should be assigned the right to access
all contents of certain concepts and relations in the
Unconstrained Conceptual Model. It calls for a mix
of model and metamodel capabilities, thus extending
the ideas exposed in section 5.
A serious shortcoming of Relation Algebra is
that it lacks arithmetic and temporal capabilities: it
cannot express calculations such as 'add 18% VAT'
or comparisons like 'if born before 1980'. Support
for this kind of rules will greatly enhance usability,
provided that the orthogonality of the language and
most importantly, the clear and uniform expression
of declarative rules in if-then syntax is safeguarded.
6.3 Future Research
We indicate some areas of ongoing research that
may improve the applicability of our approach,
methods, and tools for business rules design.
Currently, texts available for explanations in the
user interface are only static. Ongoing research aims
to determine what instructions or explanations in
which interfaces are most helpful to achieve high-
quality designs (Michels, 2011).
Integration of our language with the typical IT-
domain of Semantic Web Rule Language is being
researched (Grosof, 2013). The aim is to improve
the expressive power without compromising
orthogonality of the language and comprehensibility
of the if-then syntax of rules.
Interface design is an ongoing area of research.
In this paper, we proposed to compose and then
compile scripts. But instead of compiling, an inter-
pretative way of working might provide better
support for the designer and business stakeholders.
Research is being conducted to develop the
reflective meta-modelling approach, its vocabulary
and the rules of rule design. The idea is to build a
generator from this; a generator that is capable of
converting any rule-based design into a fully
functional and compliant prototype application.
The vision is that in the future, stakeholders may
formulate and validate their own business rules, and
do so in a language with enough precision to enable
a straightforward implementation in computer appli-
cations, without the intervention of IT specialists.
REFERENCES
Akbari I., Yan B.. Visualizing SWRL Rules. At ceur-
ws.org
Andreescu A., Mircea M., 2014. Issues and Challenges of
Business Rules Modeling in Software Systems for
Business Management. Informatica Economică 18(1)
Bajwa I.S., Lee M.G., Bordbar B., 2011. SBVR Business
Rules Generation from Natural Language
Specification. AAAI Spring Symposium: AI for
Business Agility
Beckner M., 2014. Custom Business Rules. BizTalk 2013
EDI for Health Care, Apress. p.105-116
Bjekovic M., Proper H.A., 2013. Challenges of Modelling
Landscapes. BMSD – Business Modeling and
Software Design, 3rd Int. Symposium, p.11-22.
Boley H., Paschke A. et al., 2010. RuleML 1.0:
overarching specification of web rules. LNCS 6403(4)
p.162-178
Business Rules Manifesto 2003. Edited RG Ross. At
www.businessrulesgroup.org.
Date C., 1981. Referential integrity. VLDB.
Decker H., Martinenghi D., 2006. A relaxed approach to
integrity and inconsistency in databases. Logic for
Programming, AI, and Reasoning, Springer.
Dietz J.L.G., 2008. On the Nature of Business Rules.
Advances in Enterprise Engineering. Springer. 10. p.1-
15.
Edward J.C., Timothy R., Rick K., 2011. Role
Engineering: Methods and Standards. IT Professional.
13: p.54-57.
FBM Working Group, 2011. Fact Based Modelling. At
www.factbasedmodeling.eu/Data/sites/1/media/FBM1
002WD06.pdf.
Fuchs N.E., Kaljurand K., Kuhn T., 2008. Attempto
Controlled English for knowledge representation.
Reasoning Web, Springer p.104-124
Grosof B., Kifer M., 2013. Rulelog: Syntax and Semantics.
doi=10.1.1.359.9882
Halpin T., 2011. Fact-Orientation and Conceptual Logic.
15th IEEE International on Enterprise Distributed
Object Computing Conference p.14-19
Hay D., Healy K.A., 2000. Defining Business Rules ~What
Are They Really? At www.businessrulesgroup.org/
first_paper/BRG-whatisBR_3ed.pdf.
Hoare CAR, 1985. Communicating Sequential Processes.
Prentice-hall Englewood Cliffs
Horrocks I., Patel-Schneider P.F., et al., 2004. SWRL: A
semantic web rule language combining OWL and
RuleML. W3C Member submission
Kardasis P., Loucopoulos P., 2004. Expressing and
organising business rules. Information and Software
Technology 46(11) p.701-718
Lamrani M., El Amrani Y., Ettouhami A., 2013. On
Formalizing Predefined OCL Properties. International
Journal of Computer, Information Science and
Engineering 7(1)
Maddux R.D., 2006. Relation algebras. Studies in Logic
and the Foundations of Mathematics. Elsevier. Vol
150. p. 289-525.
Fourth International Symposium on Business Modeling and Software Design
72

Michels G. et al., 2011. Ampersand. Relational and
Algebraic Methods in Computer Science. Eds H. de
Swart. Springer 6663. p.280-293.
Moody D 2005. Theoretical and practical issues in
evaluating the quality of conceptual models. Data &
Knowledge Engineering 55(3) p.243-276
Object Management Group, 2008. SBVR: Semantics of
Business Vocabulary and Business Rules, Version 1.0.
At doc.omg.org/formal/08-01-02.pdf.
Poulovassilis A., Papamarkos G., Wood P.T., 2006. Event-
condition-action rule languages for the semantic web.
EDBT 2006, Springer. p.855-864
Quartel D., Engelsman W., et al. 2009. A Goal-oriented
requirements modelling language for enterprise archi-
tecture. Enterprise Distributed Object Computing.
Ross R.G., Lam G.S.W., 2011. Building Business
Solutions: Business Analysis with Business Rules.
Business Rules Solutions LLC
RuleSpeak, 2014. RuleSpeak Sentence Forms, Specifying
Natural-Language Business Rules. At rulespeak.com.
Schön D.A., 1992. Designing as reflective conversation
with the materials of a design situation. Knowledge-
Based Systems 5(1) p.3-14.
Wedemeijer L., 2012. A comparison of Two Business
Rules Engineering Approaches. BMSD – Business
Modeling and Software Design, 2nd Int. Symposium,
p.113-121.
Weigand H., van den Heuvel W.J., Hiel M., 2011.
Business policy compliance in service-oriented
systems. Information Systems 36(4) p.791-807.
A Relation-Algebra Language to Specify Declarative Business Rules
73
