Noise Analysis of Programmable Gain Analog to Digital Converter

for Integrated Neural Implant Front End

Amir Zjajo, Carlo Galuzzi and Rene van Leuken

Circuits and Systems Group, Delft University of Technology, Mekelweg 4, 2526 CD, Delft, The Netherlands

Keywords: Noise, Programmable Gain Amplifiers, Neural Implant Front End, Analog to Digital Converters.

Abstract: Integrated neural implant interface with the brain using biocompatible electrodes to provide high yield cell

recordings, large channel counts and access to spike data and/or field potentials with high signal-to-noise

ratio. By increasing the number of recording electrodes, spatially broad analysis can be performed that can

provide insights into how and why neuronal ensembles synchronize their activity. However, the maximum

number of channels is constrained with noise, area, bandwidth, power, thermal dissipation and the

scalability and expandability of the recording system. In this paper, we characterize the noise fluctuations on

a circuit-architecture level for efficient hardware implementation of programmable gain analog to digital

converter for neural signal-processing. This approach provides key insight required to address signal-to-

noise ratio, response time, and linearity of the physical electronic interface. The proposed methodology is

evaluated on a prototype converter designed in standard single poly, six metal 90-nm CMOS process.

1 INTRODUCTION

Bio-electronic interfaces allow the interaction with

neural cells by both recording, to facilitate early

diagnosis and predict intended behavior before

undertaking any preventive or corrective actions

(Nicolelis, 2001), or stimulation devices, to prevent

the onset of detrimental neural activity such as that

resulting in tremor. Monitoring large scale neuronal

activity and diagnosing neural disorders has been

accelerated by the fabrication of miniaturized micro-

electrode arrays, capable of simultaneously

recording neural signals from hundreds of channels

(Frey, 2007). By increasing the number of recording

electrodes, spatially broad analysis of local field

potentials can be performed that can provide insights

into how and why neuronal ensembles synchronize

their activity. Studies on body motor systems has

uncovered how kinematic parameters of movement

control are encoded in neuronal spike time-stamps

(Georgopoulos, 1986) and inter-spike intervals

(Chae, 2009). Neurons produce spikes of nearly

identical amplitude near to the soma, but the

measured signal depend on the position of the

electrode relative to the cell. Additionally, the signal

quality in neural interface front-end, beside the

specifics of the electrode material and the

electrode/tissue interface, is limited by the nature of

the bio-potential signal and its biological

background noise, dictating system resources.

For any portable or implantable device, micro-

electrode arrays require miniature electronics locally

to amplify the weak neural signals, filter out noise

and out-of band interference and digitize for

transmission. A single-channel (Yin, 2007) or a

multi-channel integrated neural amplifiers and

converters provide the front-line interface between

recording electrode and signal conditioning circuits

and thus face critical performance requirements.

Multi-channel, fully differential designs allow for

spatial neural recording and stimulation at multiple

sites (Shahrokhi, 2010; Gao, 2012; Han, 2013). The

maximum number of channels is constrained with

noise, area, bandwidth, power (Chae, 2008), which

has to be supplied to the implant from outside,

thermal dissipation i.e. to avoid necrosis of the

tissues even by a moderate heat flux (Seese, 1998)

and the scalability and expandability of the

recording system. The block diagram of a typical

neural recording system architecture is illustrated in

Figure 1(a). When a neuron fires an action potential,

the cell membrane becomes depolarized by the

opening of voltage-controlled neuron channels

leading to a flow of current both inside and outside

the neuron.

Zjajo A., Galuzzi C. and van Leuken R..

Noise Analysis of Programmable Gain Analog to Digital Converter for Integrated Neural Implant Front End.

DOI: 10.5220/0005167400050012

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2015), pages 5-12

ISBN: 978-989-758-071-0

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

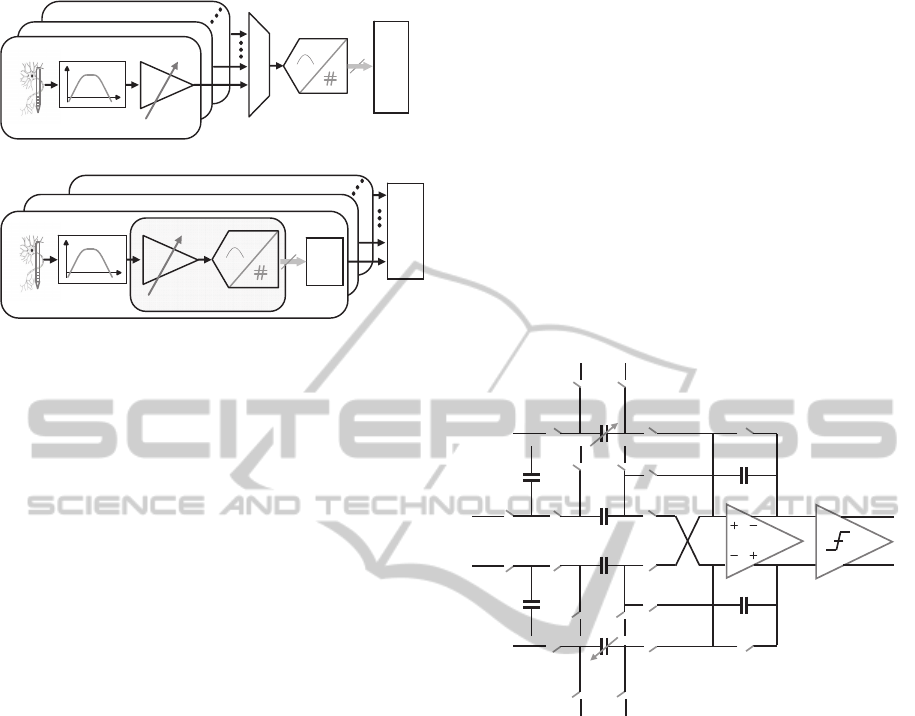
Ch #2

PGA BP-LNA

Ch #1

Analog mux

ADC

Ch #M

Ch #2

Ch #M

Serial

Data

ADC PGA BP-LNA

Ch #1

Figure 1: Multichannel neural interfaces: a) Multiplexing

an ADC between M channels, b) An ADC per channel

with serial interfacing.

Since extracellular media is resistive (de Zeeuw,

2011), the extracellular potential is approximately

proportional to the current across the neuron

membrane (Kölbl, 2010). The membrane roughly

behaves like an RC circuit and most current flows

through the membrane capacitance (West, 1991).

The data acquired by the recording electrodes are

conditioned using analog circuits. As a result of the

small amplitude of neural signals and the high

impedance of the electrode tissue interface,

amplification and band-pass filtering of the neural

signals is performed before the signals can be

digitized by a successive approximation register

(SAR)-based analog to digital converter (ADC)

(Harpe, 2013).

To avoid the large capacitive DACs found in the

SAR ADC, to lower demands on driving capabilities

of the amplifier and relax power, noise and cross-

talk requirements, in the alternative architecture

illustrated in Figure 1(b), the programmable gain

amplifier (PGA) and ADC are combined and

embedded in every recording channel. The

programmable gain analog to digital converter (PG

ADC) implements simultaneously both signal

acquisition and amplification, and data conversion.

As illustrated in Figure 2 (Rodríguez-Pérez, 2012),

the schematic incorporates a fully-differential

operational transconductance amplifier (OTA), a

comparator and circuitry for control of the

acquisition and amplification operation set by the

clock phases φ

, φ

and φ

and output generation

data conversion operation, controlled by the clock

phases φ

and φ

The recorded signals are capacitively coupled to

the input of the amplifier to reject the dc

polarization. The differential input signal is sampled,

amplified by the capacitance ratio (gain G

adjustable by implementing C

as a programmable

capacitor array, G

), and transferred to the

integration capacitors C

at the feedback loop of the

OTA. At data conversion operation, the differential

signal stored in C

is converted to digital domain by

successively adding or subtracting binary-scaled

versions of the reference voltage to the integration

capacitors. Voltage addition or subtraction is

implemented by means of the four cross-coupled

switches controlled by the signals φ

and φ

Digital representation of the output signals are then

sequentially stored in SAR register for further

processing.

ref

comp

1

vcm

Figure 2: Schematic of programmable gain ADC.

A low-power monolithic digital signal

processing (DSP) unit provides additional filtering

and executes a spike discrimination and sorting

algorithms (Harrison, 2007). The relevant

information is then transmitted to an outside receiver

through the transmitter or used for stimulation in a

closed-loop framework. Understanding the role of

noise in such systems is one of the central challenges

in the heterogeneous neural simulation and neural

rehabilitation (Harrison, 2008). In this paper, we try

to characterize the noise fluctuations on a circuit-

architecture level for efficient hardware

implementation of neural signal-processing circuitry.

This approach provides key insight required to

address signal-to-noise ratio (SNR), response time,

and linearity of the physical electronic interface (i.e.,

saturation level).

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

2 NOISE CHARACTERIZATION

For discrete-time analog signal-processing circuits,

analog signals are acquired and processed

consecutively, and a sample of the signal is taken

periodically controlled by a clock signal. As the

sampling circuit cannot differentiate the noise from

the signal, part of this signal acquisition corresponds

to the instantaneous value of the noise at the moment

the sampling takes place. In this context, when the

sample is stored as charge on a capacitor, the root-

mean-square total integrated thermal noise voltage is

kT/C

, where kT is the thermal energy. This noise

usually comprises two major contributions - the

channel noise of the switches, which is a function of

the channel resistance and the OTA noise. The OTA

output noise is in most cases dominated by the

channel noise of the input transistors, where the

thermal noise and the 1/f noise both contribute. If the

input transistors of the OTA are biased in saturation

region to derive large transconductance g

, impact

ionization and hot carrier effect will enhance their

thermal noise level (Enz, 2000). Similarly, the 1/f

noise increases as well due to the reduced gate

capacitance resulted from finer lithography and

therefore shorter minimum gate length. As a

consequence, an accurate consideration of the

intrinsic noise sources in such a circuit should have

the thermal noise of switches and all amplifier

noises readily included. Nevertheless, the input-

referred noise v

(the total integrated output noise as

well) still takes the form of kT/C with some

correction factor χ

/ CkTv





(1)

2.1 Noise Analysis of Programmable

Gain Analog to Digital Converter

A fundamental technique to reduce the noise level,

or to increase the signal-to-noise ratio of a

programmable gain ADC, is to increase the size of

the sampling capacitors, by over-sampling or with

calibration. However, for a fixed input bandwidth

specification, the penalty associated with these

techniques is the increased power consumption.

Consequently, a fundamental trade-off exists

between noise, speed, and power dissipation.

2.1.1 Kt/C Noise

During the acquisition process, kT/C noise is

sampled on the capacitors C

along with the input

signal. To determine the total noise charge sampled

onto the capacitor network, noise charge Q

integrated over all frequencies

)(

)(1

)(

OTAp

OTApon

OTApns

CCCkT

CCCRj

CCCV

















(2)

where R

is resistance of the switch, V

is noise

source, C

is parasitic capacitance and C

OTA

is the

input capacitance of the OTA. Then in the

conversion mode, the sampling capacitor C

, which

now contains the signal value and the offset of the

OTA, is connected across the OTA. The total noise

charge will cause an output voltage of





)(

CCC

OTAp

outns









(3)

where β is the feedback factor. For differential

implementation of the circuit, the noise power of the

previous equation increases by a factor of 2

assuming no correlation between positive side and

negative side, since the uncorrelated noise adds in

power. Thus, input referred noise power, which is

found by dividing the output noise power by the

square of the gain (G

) is given by

)(

outns

inns





(4)

2.1.2 OTA Noise in Conversion Mode

The resistive channel of the MOS devices in OTA

also has thermal noise and contributes to the input

referred noise of the PG ADC circuit. The noise

power at the output is found from









LTom

nsjoutns

disHv

























)(

(5)

where R

is the output resistance and C

is the

capacitance loading at the output





OTApLLT

CCCC 









(6)

The thermal noise coefficient γ depends on the

effective mobility and channel length modulation

(Jindal, 2006); it is 2/3 for older technology nodes

and between 0.6 and 1.3 for submicron technologies

(Ou, 2011). The optimum gate capacitance of the

OTA is proportional to the sampling capacitor

OTA,opt

=χ

, where χ

is a circuit-dependent

proportionality factor. The drain current I

yields







(7)

NoiseAnalysisofProgrammableGainAnalogtoDigitalConverterforIntegratedNeuralImplantFrontEnd

where µ is the carrier mobility, C

is the gate oxide

capacitance, ω

is the gain-bandwidth product, and

W and L are the channel width and length. Assuming

β»1, and gain of the conversion operation

, the input referred noise variance is

inns

)(







(8)

2.1.3 Total Input Referred Noise

The noise from acquisition and conversion mode can

be added together to find the total input referred

noise assuming that two noise sources are

uncorrelated. Using the results from (4) and (8), the

total input referred noise power for differential input

is given by

CGCG

inns



















)(









(9)

For a noise dominated by kT/C, the power

consumption is found as

max

VkTSNRL

VIP

DDDsi









(10)

For a given speed requirement and signal swing, a

two times reduction in noise voltage requires a four

times increase in the sampling capacitance value and

the OTA size. This means that the PG ADC circuit

power quadruples for every additional bit resolved

for a given speed requirement and supply voltage as

illustrated in Figure 3 and Figure 4. Notice that for a

small sampling capacitor values, thermal noise limits

the SNR, while for a large sampling capacitor, the

SNR is limited by the quantization noise and the

curve flattens out. Improving the power efficiency

beyond topological changes of the OTA and supply

voltage reduction require smart allocation of the

biasing currents. Hence, techniques such as current

reuse (Song, 2013; Zou, 2013), time multiplexing

(Chae, 2009; Zou, 2013) and adaptive duty-cycling

of the entire analog front end (Lee, 2010;

Abdelhalim, 2011) can be used to improve power

efficiency by exploiting the fact that neurons spikes

are irregular and low frequency. Choosing the OTA

bandwidth too high increases the noise and

additionally demands unnecessarily low on-

resistance of the switches and thus large transistor

dimensions. The optimum time constant remains

constant regardless of the circuit size (or I

) because

scales together with C

and the parasitic

capacitance C

Figure 3: Maximum achievable SNR for different

sampling capacitor values and resolutions.

Figure 4: SNR versus power dissipation.

The choice of the hold capacitor value is a trade-

off between noise requirements on the one hand and

speed and power consumption on the other hand.

The sampling action adds kT/C noise to the system

which can only be reduced by increasing the hold

capacitance C

. A large capacitance, on the other

hand, increases the load of the operational amplifier

and thus decreases the speed for a given power. The

OTA size and its bias current for a given speed

requirement and minimum power dissipation are

determined using τ-vs.-C

curves as in Figure 5.

Note that for low frequency operation (where τ/τ

large), the C

OTA

that achieves the minimum power

dissipation for given settling time and noise

requirements, usually does not correspond to the

minimum time constant point. This is a consequence

of setting the C

OTA

ratio of the circuit to the

minimum time constant point, which requires larger

OTA

and results in power increase and excessive

bandwidth.

Near the speed limit of the given technology

(where the ratio τ/τ

is small), however, the

difference in power between the minimum power

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

point and the minimum time constant point becomes

smaller as the stringent settling time requirement

forces the C

OTA

ratio (Figure 6) to be at its

optimum value to achieve the maximum bandwidth.

2.2 The OTA Noise

The OTA in PG ADC circuit has some unique

requirements; the most important is the input

impedance, which must be purely capacitive so as to

guarantee the conservation of charge. Consequently,

the OTA input has to be either in the common

source or the source follower configuration. Another

characteristic feature is the load at the OTA output,

which is typically purely capacitive and as a result,

the OTA output impedance must be high. The

benefit of driving solely capacitive loads is that no

output voltage buffers are required.

Figure 5: Closed loop normalized time constant versus

hold capacitance C

for different biasing conditions; case

for C

=3C

, C

. The time constant is normalized to the

(=1/f

t,intrinsic

) of the device, which is approximately

Figure 6: Optimum gate capacitance C

OTA,opt

versus hold

capacitance C

for different loading and parasitic

conditions.

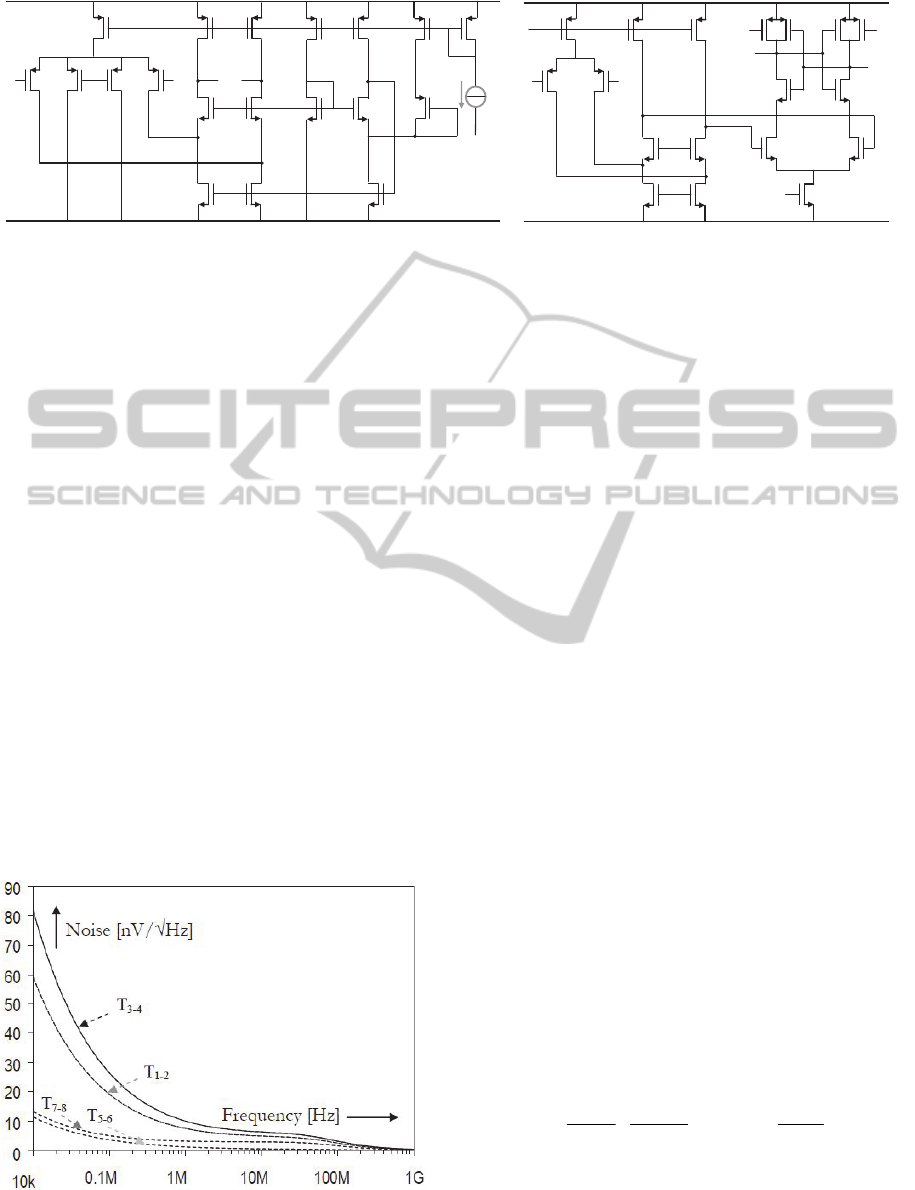
The implemented folded-cascode OTA and

dynamic latch are illustrated in Figure 7. The input

stage of the OTA is provided with two extra

transistors T

and T

in a common-source

connection, having their gates connected to a desired

reference common-mode voltage at the input, and

their drains connected to the ground (Bult, 1990).

The advantage of this solution is that the common-

mode range at the output is not restricted by a

regulation circuit, and can approach a rail-to-rail

behavior very closely.

The transistors of the output stage have two

constrains: the g

of the cascading transistors T

5,6

must be high enough, in order to boost the output

resistance of the cascode, allowing a high enough dc

gain and the saturation voltage of the active loads

3,4

and T

7,8

must be maximized, in order to reduce

the extra noise contribution of the output stage.

These considerations underline a tradeoff between

fitting the saturation voltage into the voltage

headroom and minimizing the noise contribution. A

good compromise is to make the cascading

transistors larger than the active loads: in such a way

the g

of the cascading transistors is maximized,

boosting the dc gain, while their saturation voltage is

reduced, allowing for a larger saturation voltage for

the active loads, without exceeding the voltage

headroom. The output SNR is equal to

8,74,32,1

2,1

mmm

outm

out

ggg

RgA

SNR









(11)

where A is the amplitude of the input signal and R

out

denotes the open-loop output resistance of the OTA.

From (11) can be concluded that in order to

maximize the output SNR, C

must be maximized,

which means that bandwidth must be minimized.

The noise contribution of the individual

transistors are shown in Figure 8. The input-referred

noise of the OTA input pair is reduced by increasing

the g

, increasing the current, or increasing the

aspect ratio of the devices. The effect of the last

method, however, is partially canceled by the

increase in the noise excess factor. When referred to

the OTA input, the noise voltages of the transistors

used as current sources (or mirrors) in the first stages

are multiplied by the g

of the device itself and

divided by the g

of the input transistor, which again

suggests that maximizing input pair g

minimizes

noise. It can be further reduced by decreasing the g

of the current sources. Since the current is usually

set by other requirements, the only possibility is to

decrease the aspect ratio of the device. This leads to

an increase in the gate overdrive voltage, which, as a

positive side effect, also decreases γ.

NoiseAnalysisofProgrammableGainAnalogtoDigitalConverterforIntegratedNeuralImplantFrontEnd

VSS

inn

VDD

inp

T10 T11

T9 T12 T14

outn

outp

T17

T19

T13 T15

T18

T16

Ibias

inp

T18

VSS

VDD

inn

outp

outn

clk

T10 T11

T15 T14

T12 T13

T17

T6 T5

T16

T8 T7

bias

T4 T3

(a) (b)

Figure 7: a) OTA schematic, b) Comparator schematic.

Increasing L to avoid short channel effects is also

possible, although with a constant aspect ratio it

increases the parasitic capacitances.

The dynamic latch illustrated in Figure 7(b)

consists of pre-charge transistors T

and T

, cross-

coupled inverter T

12-13

and T

15-16

, differential pair T

and T

and switch T

, which prevent the static

current flow at the resetting period (Kobayashi,

1993). When the latch signal is low (resetting

period), the drain voltages of T

10-11

are V

-V

and

their source voltage is V

below the latch input

common mode voltage. Therefore, once the latch

signal goes high, the n-channel transistors T

11-13

immediately go into the active region. Because each

transistor in one of the cross-coupled inverters turns

off, there is no static power dissipation from the

latch once the latch outputs are fully developed. A

large portion of the total comparator current is

allocated to the input branches to boost the input g

Similarly, the noise from the non-gain element i.e.

the load transistor, is minimized, by applying small

biasing current. Additionally, small width and large

length for their gate dimensions is chosen.

Figure 8: Noise contribution of the individual transistors in

the OTA.

3 EXPERIMENTAL RESULTS

The time series representation of an neuron signal

(Figure 9) are composed of a spike burst, plus

additive Gaussian white noise (grey area with 1000

randomly selected neural channel compartments). In

typical electrode-tissue interface, we are relying on

the current measurement to sense these neural

signals. Hence, by maintaining a constant current

density, the relative uncertainty of the current

becomes inversely proportional to the square of the

interface area. The electrode noise spectral density

has an approximate dependence of -10 dB/dec for

small frequencies. However, for frequencies higher

than 1-10 kHz, capacitances at the interface form the

high-frequency pole and shape both the signal and

the noise spectrum; the noise is low-pass filtered to

the recording amplifier inputs. After band-pass

filtering and amplification, the noisy neural signal is

further processed with programmable gain analog to

digital converter. The fluctuation of the voltage on

the sampling capacitor is inversely proportional to

the capacitance (the variance of the capacitor voltage

is kT/C at any given time). This implies that with

scaling, the uncertainty of the sampled voltage

increases. It can be seen that in both scenarios, in

electrode-tissue interface and in PG ADC, the noise

in the neural interface front end greatly increases as

the interface size reduces. The interface’s input

equivalent noise voltage decreases as the gain across

the amplifying stages increase, e.g. the ratio of the

square of the signal power over its noise variance

can be expressed as































 2

),(

)(

iampns

jelectrodensneuralns

vGvvASNR

(12)

where v

ns(amp,i)

represents the variance of the noise

added by the ith amplification stage with gains G

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

0 5 10 15 20 25

-80

-60

-40

-20

Membrane potential [mV]

Time [ms]

Figure 9: Statistical voltage trace of neuron cell activity;

grey area - voltage traces from 1000 randomly selected

neural channel compartments.

The variance of the electrode is denoted as

ns(electrode)

and v

ns(neural)

is variance of the biological

neural noise. The observed SNR of the system also

increases as the system is isomorphically scaled up,

which suggests a fundamental trade-off between

SNR and speed of the system. This lower bound on

the speed in a converter loop is primarily a function

of the technology’s gate delay and kT/C noise

multiplied by the number of SAR cycles necessary

for one conversion.

All PG ADC simulations were performed with a

1.2 V supply voltage at room temperature (25ºC).

Spectral signature of PG ADC is illustrated in Figure

10. The circuit offers a programmable amplification

of 0-18 dB by digitally scaling the input capacitance

. As shown in Figure 11, the Signal-to-Noise and

Distortion Ratio (SNDR), Spurious-Free Dynamic

Range (SFDR) and Total Harmonic Distortion

(THD) remain constant at different gain settings.

The THD in the range of 10-100 kS/s is above 54 dB

for f

of 5 kHz (Figure 12). Within the bandwidth of

neural activity of up to 5 kHz, SNDR is above 44 dB

and SFDR more than 57 dB. The degradation with a

higher input signal is mainly due to the parasitic

capacitance, clock non-idealities and substrate

switching noise.

0.1 1 10 50

-120

-100

-80

-60

-40

-20

Frequency [kHz]

Figure 10: Spectral signature of programmable gain A/D

converter-two tone test.

1 2 3 4 5 6 7 8

Gain

SFDR, THD, SNDR [dB]

SFDR

SNDR

THD

Figure 11: SFDR, SNDR and THD versus gain settings.

10 20 30 40 50 60 70 80 90 100

Sampling frequency [kHz]

SFDR, THD, SNDR [dB]

SFDR

SNDR

THD

Figure 12: SFDR, SNDR and THD versus sampling

frequency with f

=5 kHz and gain set to one.

Parasitic capacitance decreases the feedback

factor resulting in an increased settling time

constant. The non-idealities of clock such as clock

jitter, non-overlapping period time, finite rising and

fall time, unsymmetrical duty cycle are another

reason for this degradation. The three latter errors

reduce the time allocated for the setting time.

4 CONCLUSIONS

The high density of neurons in neurobiological

tissue requires a large number of electrodes for

accurate representation of neural activity. To

develop neural prostheses capable of interfacing

with single neurons and neuronal networks, multi-

channel neural probes and the electrodes need to be

customized to the anatomy and morphology of the

recording site. The increasing density and the

miniaturization of the functional blocks in these

multi-electrode arrays, however presents significant

circuit design challenge in terms of area, bandwidth,

power, and the scalability, programmability and

expandability of the recording system. In this paper,

for one such functional block, programmable analog

to digital converter, we evaluate trade-off between

noise, speed, and power dissipation and characterize

the noise fluctuations on a circuit-architecture level.

NoiseAnalysisofProgrammableGainAnalogtoDigitalConverterforIntegratedNeuralImplantFrontEnd

This approach provides key insight required to

address SNR, response time, and linearity of the

physical electronic interface.

ACKNOWLEDGEMENTS

This research was supported in part by the European

Union and the Dutch government as part of the

CATRENE program under Heterogeneous

INCEPTION project.

REFERENCES

Abdelhalim, K., Genov, R., 2011, CMOS DAC-sharing

stimulator for neural recording and stimulation arrays,

Proceedings of IEEE International Symposium on

Circuits and Systems, pp. 1712-1715.

Bult, K., Geelen, G., 1990, A fast-settling CMOS op amp

for SC circuits with 90-dB DC gain, IEEE Journal of

Solid-State Circuits, vol. 25, no. 6, pp. 1379-1384.

Chae, C., et al., 2009, A 128-channel 6 mw wireless

neural recording IC with spike feature extraction and

UWB transmitter, IEEE Transactions on Neural

Systems and Rehabilitation Engineering, vol. 17, no.

4, pp. 312-321.

Chae, M.S., Liu, W., Sivaprakasham, M., 2008, Design

optimization for integrated neural recording systems,

IEEE Journal of Solid-State Circuits, vol. 43, no. 9,

pp. 1931-1939.

Enz, C., Cheng, Y. 2000, MOS transistor modeling for RF

IC design, IEEE Journal of Solid-State Circuits, vol.

35, no. 2, pp. 186-201.

Frey, U., et al., 2007, An 11k-electrode 126-channel high-

density micro-electrode array to interact with

electrogenic cells, IEEE International Solid-State

Circuits Conference Digest of Technical Papers, pp.

158-159.

Gao, H, et al., 2012, HermesE: a 96-channel full data rate

direct neural interface in 0.13um CMOS, IEEE

Journal of Solid-State Circuits, vol. 47, no. 4, pp.

1043-1055.

Georgopoulos, A.P., Schwartz, A.B., Kettner, R.E., 1986,

Neuronal population coding of movement direction,

Science, vol. 233, no. 4771, pp. 1416-1419.

Han, D., et al., 2013, A 0.45 V 100-channel neural-

recording IC with sub-μW/channel comsumption in

0.18 μm CMOS, IEEE Transactions on Biomedical

Circuits and Systems, vol. 7, no. 6, pp. 735-746.

Harpe, P., Cantatore, E., van Roermund, A., 2013, A

10b/12b 40 kS/s SAR ADC with data-driven noise

reduction achieving up to 10.1b ENOB at 2.2

fJ/conversion-Step, IEEE Journal of Solid-State

Circuits, vol. 48, no. 12, pp. 3011-3018.

Harrison, R. R., et al., 2007, A low-power integrated

circuit for a wireless 100-electrode neural recording

system, IEEE Journal of Solid-State Circuits, vol. 42,

no. 1, pp. 123-133.

Harrison, R., 2008, The design of integrated circuits to

observe brain activity, Proceedings of IEEE, vol. 96,

no. 7, pp. 1203-1216, 2008.

Jindal, R.P., 2006, Compact noise models for MOSFETs,

IEEE Transactions on Electron Devices, vol. 53, No.

9, pp. 2051-2061.

Kobayashi, T., Nogami, K., Shirotori, T., Fujimoto, Y.,

1993, A current-controlled latch sense amplifier and a

static power-saving input buffer for low-power

architecture, IEEE Journal of Solid-State Circuits, vol.

28, no. 4, pp. 523-527.

Kölbl, F., et al., 2010, In vivo electrical characterization of

deep brain electrode and impact on bio-amplifier

design, Proceedings of IEEE Biomedical circuits and

Systems Conference, pp. 210-213.

Lee, J., Rhew, H.-G.,Kipke, D.R., Flynn, M.P., 2010, A 64

channel programmable closed-loop neurostimulator

with 8 channel neural amplifier and logarithmic ADC,

IEEE Journal of Solid-State Circuits, vol. 45, no. 9,

pp. 1935-1945.

Nicolelis, M.A.L., 2001, Actions from thoughts, Nature,

vol. 409, pp. 403-407.

Ou, J., 2011, g

based noise analysis for CMOS analog

circuits, Proceedings of IEEE International Midwest

Symposium on Circuits and Systems, pp. 1-4.

Rodríguez-Pérez, A., et al., 2012, A 64-channel

inductively-powered neural recording sensor array,

Proceedings of IEEE Biomedical Circuits and Systems

Conference, pp. 228-231.

Seese, T.M., Harasaki, H., Saidel, G.M., Davies, C.R.,

1998, Characterization of tissue morphology,

angiogenesis, and temperature in the adaptive response

of muscle tissue to chronic heating, Laboratory

Investigation, vol. 78, no. 12, pp. 1553-1562.

Shahrokhi, F. et al., 2010, The 128-channel fully

differential digital integrated neural recording and

stimulation interface, IEEE Transactions on

Biomedical Circuits and Systems, vol. 4, no. 3, pp.

149-161.

Song, S., et al., 2013, A 430nW 64nV/VHz current-reuse

telescopic amplifier for neural recording application,

Proceedings of IEEE Biomedical Circuits and Systems

Conference, pp. 322-325.

West, A.C., Newman, J., 1991, Current distributions on

recessed electrodes, Journal of the Electrochemical

Society, vol. 138, no. 6, pp. 1620-1625.

Yin, M., Ghovanloo, M., 2007, A low-noise preamplifier

with adjustable gain and bandwidth for bio potential

recording applications, IEEE International Symposium

on Circuits and Systems, pp. 321-324.

Zeeuw, de, C.I., et al., 2011, Spatiotemporal firing

patterns in the cerebellum, Nature Reviews

Neuroscience, vol. 12, no. 6, pp. 327-344.

Zou, X., et al., 2013, A 100-channel 1-mW implantable

neural recording IC, IEEE Transactions on Circuits

and Systems I: Regular Papers, vol. 60, no. 10, pp.

2584-2596.

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices