
Segmentation of LG Enhanced Cardiac MRI
Kjersti Engan
1
, Valery Naranjo
2
, Trygve Eftestøl
1
, Stein Ørn
3
and Leik Woie
3
1
University of Stavanger, Stavanger, Norway
2
Labhuman, I3BH, Universitat Polit
`
ecnica de Val
`
encia, Valencia, Spain
3
Stavanger University Hospital, Stavanger, Norway
Keywords:
Cardiac MRI, Segmentation, Late Gadolinium enhanced MRI.
Abstract:
In this paper a method for segmentation of the endocardium in Late Gadolinium Enhanced Cardiac Magnetic
Resonance (LGE-CMR) images is presented and combined with a previously proposed method for segmen-
tation of the epicardium. The method is fully automatic and based on utilizing a priori knowledge about the
type of images. No other image modalities, like CINE images, are used. Using a combination of a rough a
priori model and preprocessed images, an a posteriori model is built. The final segmentation step is performed
in the polar domain. We compare our results on a set of 395 images from 54 patients with segmentation using
marker controlled watershed with different gradient images and different markers. The proposed method gives
a mean Dice and Jaccard indices over all images as 0.85 and 0.74 respectively.
1 INTRODUCTION
Myocardial Infarction (MI) caused by cardiac is-
chemia is one of the major causes of death and dis-
ability in the world. MI is defined by pathology as
myocardial cell death due to insufficient blood sup-
ply. Dead myocardial cells are replaced by myocar-
dial scar (Thygesen et al., 2007). After MI it is
important to evaluate the degree of damage. Car-
diac Magnetic Resonance (CMR) imaging is a non-
invasive method for evaluating the myocardium. To
be able to distinguish the scar, i.e. the dead cells,
from normal myocardial tissue, a gadolinium based
contrast agent is most frequently used. Images that
visualize dead tissue can be generated by the use of
the late Gadolinium Enhancement Cardiac Magnetic
Resonance (LGE-CMR) technique. This paper is ad-
dressing the problem of automatically segmenting the
myocardium in LGE-CMR images of the left ventri-
cle.
Healthy myocardium appears very dark in CMR
images, however the edges of the heart in LGE-
CMR images where the patient has a scar in the my-
ocardium are sometimes very weak or non-existing
since the scarred areas will take intensity levels close
to the blood pool or the surrounding areas. This
makes automatic segmentation of the myocardium in
LGE-CMR images difficult. In many hospitals to-
day the segmentation of the myocardial muscle is per-
formed manually or semi-automatically by expert car-
diologists. This can be time-consuming work, and the
results will have a degree of inter- and intra-observer
variability.
1.1 Data Material
The Department of Cardiology at Stavanger Univer-
sity Hospital provided LGE-CMR images of 54 pa-
tients with varying number of slices, giving 395 im-
ages. All patients have had myocardial infarction
prior to the examination, and 20 of them had profound
scars and was later implanted with Implantable Car-
dioverter Defibrillator (ICD). CMR was performed
using 1.5 T Philips Intera R 8.3, typical pixel size
of 0.8 × 0.8mm
2
, covering the whole ventricle with
short-axis slices of 10 mm thickness, without inter-
slice gaps. An example of all the 8 slices from one
patient is seen in Figure 1, and the endocardium is the
inner border of the dark ring (partly bright because
of scar) approximately in the middle of each slice.
All left ventricle, short axis view slices of all patients
were manually segmented by expert cardiologists to
provide a true marking. The true heart center used in
some experiments referrers to the centroid of the pix-
els in the myocardium extracted from these true endo-
and epicardium markings.
47
Engan K., Naranjo V., Eftestøl T., Ørn S. and Woie L..
Segmentation of LG Enhanced Cardiac MRI .
DOI: 10.5220/0005169200470055
In Proceedings of the International Conference on Bioimaging (BIOIMAGING-2015), pages 47-55
ISBN: 978-989-758-072-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: LGE-MRI slices of a patient with myocardial scar. Approximately at the middle of each slice there is an almost
circular and brighter area which is the bloodpool of the heart. The myocardial muscle tissue surrounding the bloodpool is
dark, and in a healthy subject it would have the appearance of a ring. In LGE-MRI, however, scarred tissue with reduced blood
flow will appear brighter. Here we see that the myocardial muscle is partly as bright as the bloodpool because of infarction
scar. The inner border of the myocardial muscle (the dark and partly bright ring) is the endocardium border. The outer border
of the myocardial muscle is called the epicardium border.
1.2 Relation to Prior Work
There have been attempts to solve the problem of au-
tomatic segmentation reported in the literature. Some
methods require manual input in the form of land-
marks or cropping of region of interest, etc (de Brui-
jne and Nielsen, 2004; Spreeuwers and Breeuwer,
2003; Heiberg et al., 2010). Others make use of ad-
ditional data as the corresponding cine MR (ODon-
nell et al., 2003; Ciofolo et al., 2008; Wei et al., 2011;
Wei et al., 2013), or a combination of cine images and
some manual input (Dikici et al., 2004). However, the
use cine-MR requires a suitable registration onto the
LGE-CMR dataset, and this includes potential diffi-
culties since patients position and holding of breath
can introduce misalignments.
In our work all results are based solely on the
LGE-CMR images. We presented a method for au-
tomatically finding the heart center in (Engan et al.,
2013b) and segmentation of the epicardium (Engan
et al., 2013a) with some early results. In this paper we
have continued this work and are presenting a method
for automatic segmentation of the endocardium. A
priori knowledge of typical heart size and shape is
used as the input, and an a posteriori probability map
is made iteratively. The final segmentation is based
on the a posteriori probability maps, and information
from all slices are taken into account. Recent work by
Alb
`
a et.al. (Alba et al., 2012), (Alba et al., 2013) is
also based on the LE-CMR images alone without the
need of cine MR sequences and corresponding reg-
istration. The 3D information and a conical model
are utilized to detect initialization, somewhat similar
to the way we find the heart center in (Engan et al.,
2013b).
2 PROPOSED METHOD
The proposed method for segmentation of the my-
ocardium is based on an iterative algorithm finding
an a posteriori probability map, where the probability
map can be interpreted as the probability of a specific
pixel belonging to the myocardium. A block diagram
of the complete system can be seen in Figure 2. The
system starts by an algorithm for automatically find-
ing the heart center from the whole LGE-CMR slices
with no pre-cropping (block 1). This part will not be
described here, but we proposed two algorithms for
solving this problem in (Engan et al., 2013b). Using
the heart center (HC) as input, an a priori model is
made (block 2), and by using the iterative algorithm
(block 3), an a posteriori probability model is found.
This a posteriori model gives a good foundation for
the last segmentation step of both the epicardium and
the endocardium. The iterative algorithm of block 3 is
important in the context of this paper, thus described
BIOIMAGING2015-InternationalConferenceonBioimaging
48

here. However a version of this was presented in (En-
gan et al., 2013a) together with some early results on
segmenting the epicardium (block 4). The main fo-
cus of this paper is block 5, segmentation of the en-
docardium. The algorithm is shown and some results
comparing with watershed segmentation of the blood-
pool is presented in the results section.
In the following, let f
i
(x), i = 1 . .. N
slice
represent
the left ventricle short axis LGE-CMR images of a
patient. x = [x
row
x
column
]
T
is the pixel position, and i
represents the slice number.
2.1 Probability Map
The LGE-CMR images are hard to segment because
the scars are bright, whereas the muscle is dark, the
scars have similar intensity levels as the blood pool in-
side the endocardium border, and the edges are some
places non-exsisting. The reason why an expert cardi-
ologist is capable of segmenting the images manually
is that the cardiologist will automatically use prior in-
formation of typical shapes and sizes of a heart. In
the left ventricle short axis view the myocardium will
more or less have the shape of a ring, and this infor-
mation has to be utilized.
We propose to use a rough a priori model of the
myocardium around the heart center for each slice im-
posed as a gaussian in the polar domain with the heart
center as the origin for all angles. µ of the gaussian
prior will correspond to the approximated radius at
the middle of the myocardium for that slice, and is
varied with the slice number. Typical values are found
from a training set, but a large variance is used in the
gaussian prior to make the a priori model robust. Af-
ter mapping to cartesian coordinates and scaling all
pixels to be within [0, 1], this gives an a priori proba-
bility map, where the probability is seen as the prob-
ability for being a pixel in the myocardium.
Using the a priori probability model as input, we
propose an iterative approach to refine the model and
make an a posteriori probability map for the my-
ocardium. At each iteration the probability model
is combined with the inverse of the original (prepro-
cessed) slices, a low pass filtering over the neighbor-
ing slices is performed, and the output is a new prob-
ability model. The inverse of the original is used be-
cause the myocardial muscle we want to segment ap-
pears dark in the images, and thus appears bright with
high values in the inverse. The algorithm is depicted
in Algorithm 1, and a brief explanation follows.
In line (3) of Algorithm 1, a morphological noise
removal of the original slices, f
i
is conducted using
the morphological center, as defined in (Soille, 2003),
and the structuring element B
mc
as a square of size
Algorithm 1: Iterative probability map algo-
rithm.
Data: CMR images f
i
(x) ∈ R
N×M
, Prior prob.
map p
i
0
(x) ∈ R
N×M
i = 1, . . . N
slice
,
Result: Posteriori prob. map,
p
i
post
(x) ∈ R
N×M
, i = 1, . . . N
slice
1 initialization: k
f inal
;
2 for i ← 1 to N
slice
do
3 f
i
prep
(x) ← β
B
mc
( f
i
) ;
4 f
i
inv
(x) =scale(ones(N, M) − f
i
prep
(x));
5 end
6 for k ← 0 to k
f inal
− 1 do
7 f
temp
(x) = p
k
(x) × f
inv
(x);
8 f
temp
(x) ← LP f iltZ( f
temp
(x)) ;
9 p
k+1
(x) ← scale( f
temp
(x));
10 end
11 p
nof
(x) = p
0
(x) × ( f
inv
(x))
k
f inal
;
12 p
post
(x) =
scale(w
1
p
k
f inal
(x) + (1 − w
1
)p
nof
(x));
13 return(p
post
) ;
3 × 3 pixels. The noise removal results in a prepro-
cessed slice, f
i
prep
(x), and the inverse of the prepro-
cessed slice is found in line (4) as f
i
inv
(x). The main it-
eration is done in line 6-10, using the previous proba-
bility map, f
temp
(x) = p
k
(x)× f
inv
(x), Low Pass (LP)
filtering over the slices, LP f iltZ( f
temp
(x)), and sub-
sequenty finding a new probability map, p
k+1
(x) by
scaling the result of the filtering. Another map is
found without filtering over the slices, p
nof
(x), di-
rectly without any iterations as (line 11): p
nof
(x) =
p
0
(x) × ( f
inv
(x))
k
f inal
. The final probability model is
a scaled and weighted sum (line 12) between p
k
f inal
(x)
and p
nof
(x). A × B denotes the Hademard product.
In Figure 3 an example patient is depicted. Top
two rows show the a priori probability map, middle
rows show the a posteriori probability map, and last
two rows shows the original images for this patient.
2.2 Segmentation
The a posteriori probability map looks promising,
but still the segmentation is challenging. The scarred
areas might appear quite dark in the probability im-
ages, thus the probability values can differ signif-
icantly at different angles. Consequently, a global
thresholding technique will not work, regardless of
the chosen threshold. The heart center at each slice,
HC
i
is an important input, and from the heart cen-
ter the probability values at all radii are evaluated at
different angles, θ ∈ [0, 2π] for both epicardium and
SegmentationofLGEnhancedCardiacMRI
49

Figure 2: Block diagram of the segmentation scheme.
endocardium segmentation. Since we know that the
endocardium borders lie within the epicardium bor-
ders, we start by finding the epicardium mask and use
that as a input for the endocardium segmentation.
The algorithm for segmenting the epicardium was
presented and explained in (Engan et al., 2013a) and
will not be repeated here. In short, the epicardium
segmentation algorithm uses the a posteriori proba-
bility map as well as the heart centers as input. A mor-
phological closed-hole preprocessing of the probabil-
ity map is done prior to a Otsu’s multilevel threshold-
ing. Using the heart center position in each slice, HC
i
,
as origin, the values after the multilevel thresholding
are interpreted in polar coordinates giving R
v
(θ, r),
where θ is the angle and r the radius. The partial
derivative of R
v
(θ, r) with respect to r is found for all
θ, D
r
(θ, r), and the first negative value of the deriva-
tive (smallest radius) is marked as a candidate epi-
cardium border point, R
i
epi
(θ), for each θ. Some final
steps are dealing with angles with missing candidate
points by looking at neighboring angles and slices.
The proposed segmentation of the endocardium
is also based on the a posteriori probability map,
p
i
post
(x) ∈ R
N×M
, i = 1, . . . N
slice
. The segmentation
of the epicardium is executed first, and a resulting epi-
cardium mask, Mask
i
epicard
(x), is used as additional
information since the endocardium must lie inside
the epicardium. A pseudocode of the algorithms for
endocardium segmentation based on the probability
maps is seen in Algorithm 2, and an explanation fol-
lows:
A multilevel version of Otsu’s method (Otsu,
1979) is used for non uniformly quantizing of p
i
post
(x)
into L levels: f
i
q
(x) = Quant
i
nonuni
(p
i
post
(x), L) (line
3). In line 4, the Hademar product between the quan-
tized probability images and the epicardium mask sets
f
i
qepi
(x) to zero outside the epicardium.
Thereafter a conversion to polar coordinates with
the heart center as the origin is performed giving
R
v
(θ, r). For each angle a candidate endocardium
point is looked for as seen in line 7.
Let R
v
(θ, 0) denote the value at the HC (heart cen-
ter) point. If there exist points in R
v
(θ, r) with value
R
v
(θ, r
l
) > R
v
(θ, 0) + 1, and r
l
1
is the point closest
to HC, then R
endo
(θ) = r
l
1
. If not, there might exist
points with value R
v
(θ, r
m
) > R
v
(θ, 0), and let r
m
1
be
the point closest to HC, then R
endo
(θ) = r
m
1
. If nei-
ther of these points exists there are no candidate point
for that specific angle at slice i.
If an angle, θ
k
, is without candidate points for
slice i, the other slices are checked to see if there ex-
ist any candidate points for θ
k
(line 13-15). If any
of the other slices have candidate points for θ
k
, the
one corresponding to the slice closest to slice i is
chosen for slice i as well. If there are no candidate
points for θ
k
for any slices, the smallest ∆
θ
to an an-
gle with a candidate point is found within slice i, ap-
proximating the candidate point for θ
k
using the same
R
endo
(θ
k
+ ∆
θ
) (line 16-18). Finally the convex hull
of all candidate points is found as the endocardium
mask, Mask
endocard
(x)) (line 22).
2.3 Postprocessing
The endocardium mask Mask
i
endocard
(x) over the
slices i = 1, . . . N
slice
are compared. If there are
segments that are only present in Mask
k
endocard
(x)
it is considered a mistake, and removed from
Mask
k
endocard
(x). If there are segments present in
all slices except Mask
j
endocard
(x), this segment is
added to Mask
j
endocard
(x). After finding the endo-
cardium mask, the perimeter is calculated. Thereafter
BIOIMAGING2015-InternationalConferenceonBioimaging
50
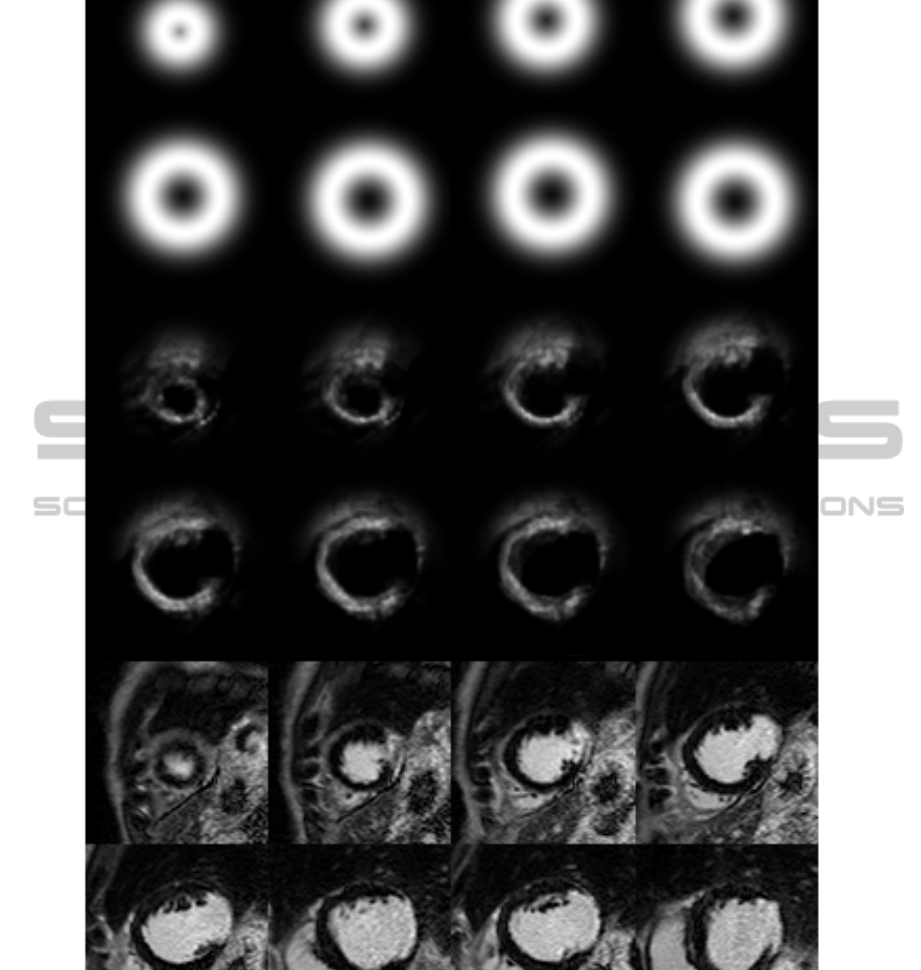
Figure 3: Top two rows, a priori probability map, second two rows, a posteriori probability map after 8 iterations, last two
rows, original images.
a Fourier Descriptor (FD) (Impedovo et al., 1978) of
this perimeter is found. The FD is lowpass filtered
resulting in a smoother perimeter and a new mask.
3 EXPERIMENTS AND RESULTS
Segmentation experiments are performed on the set of
54 patients, 395 images. Different number of levels,
L, in the multilevel version of Otsus method in Algo-
rithm 2 were tested in preliminary experiments. L=4
seemed to preform best and is used in the experiments
presented here. The number of iterations of the itera-
tive probability map scheme was set to 8. Results are
presented as Dice (Dice, 1945) and Jaccard (Jaccard,
1912) indices.
The mean and standard deviation of the resulting
Dice and Jaccard indices of the endocardium segmen-
SegmentationofLGEnhancedCardiacMRI
51
Algorithm 2: Radial Segmentation of endo-
cardium.
Data: CMR images f
i
(x) ∈ R
N×M
, Posteriori
prob. map,
p
i
post
(x) ∈ R
N×M
, i = 1, . . . N
slice
, heart
center coordinates HC
i
, Mask
i
epicard
(x) ;
Result: Mask
i
endocard
(x)
1 initialization: R
i
endo
(θ) = 0, θ ∈ [0, 2π];
2 for i = 1 to N
slice
do
3 f
i
q
(x) = Quant
i
nonuni
(p
i
post
(x), L) ;
4 f
i
qepi
(x) = f
i
q
(x) × Mask
i
epicard
(x) ;
5 for θ = 0 to 2π do
6 R
v
(θ, r) = cart2poly( f
i
qepi
(x), θ, HC
i
) ;
7 R
endo
(θ) = argmax(argmin
r
[R
v
(θ, r) >
(R
v
(θ, 0) + 1)], argmin
r
[R
v
(θ, r) >
R
v
(θ, 0)]) ;
8 end
9 R
i
endo
(θ) ← smooth(R
i
endo
(θ)) ;
10 end
11 for i = 1 to N
slice
do
12 for θ = 0 to 2π do
13 if R
i
endo
(θ) = 0 then
14 R
i
endo
(θ) ← mean(R
j
endo
(θ) 6= 0)
15 end
16 if R
i
endo
(θ) = 0 then
17 R
i
endo
(θ) ←
min
|∆
θ
|
(R
i
endo
(θ − ∆
θ
) 6= 0)
18 end
19 x
i
θ
= poly2cart(R
i
endo
(θ)) ;
20 f
i
p
(x
i
θ
) = 1;
21 end
22 Mask
i
endocard
(x) = ConvexHull( f
i
p
(x));
23 end
24 return(Mask
endocard
(x)) ;
tation are seen in Table 2 where the automatic method
for finding the heart center is used. In Table 3 the re-
sults from the same experiments, but using the true
heart center as input, are shown. In Table 1 the mean
and standard deviation of Dice index of both the en-
docardium and epicardium over all the images are
Table 1: Results for segmentation of endocardium and epi-
cardium. Dice index, averaged over 395 images. Standard
deviation in parentheses.
Endocard Epicard
Dice Dice
True HC 0.87 (0.040) 0.90 (0.034)
Automatic HC 0.85 (0.048) 0.88 (0.046)
shown comparing results using the true heart center
with the automatically found heart center. Two slices
of an example patients are seen in detail in Figure 4
for illustration.
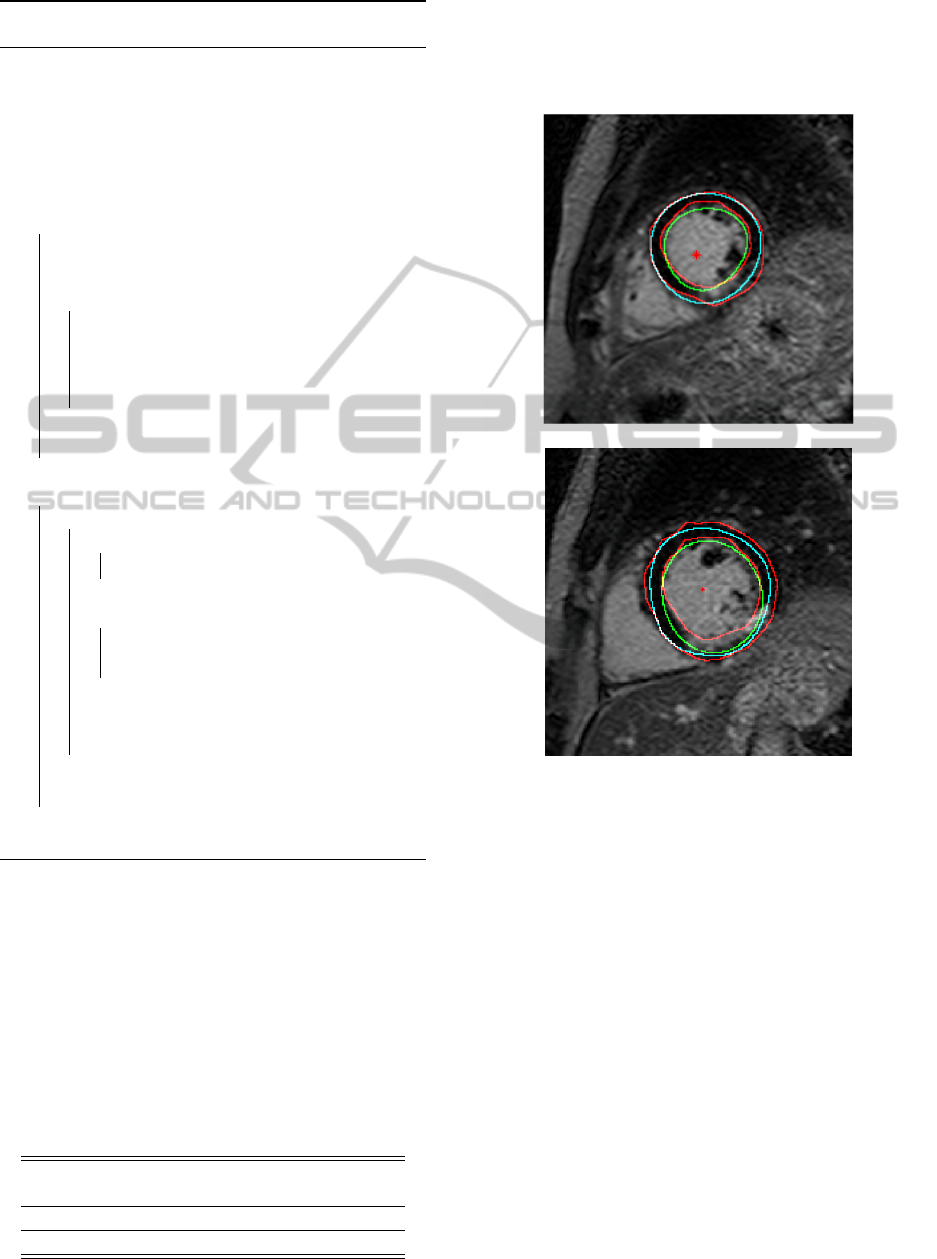
Figure 4: Segmentation results from two slices of an exam-
ple patient. manual marking performed by cardiologist in
red, automatically found heart center marked as red stars,
epicaridum contours in cyan, and endocardium contours in
green. The top slice shows well performing segmentation.
In the bottom slice the epicardium is segmented well, but
the segmentation of the endocardium fails to include the
scar in the myocardium
3.1 Comparison with Watershed
Segmentation
To compare the proposed method with a classi-
cal and successful segmentation algorithm, we have
compared with marker controlled watershed (Meyer,
1994; Soille, 2003) using different gradient images,
and different markers.
Watershed segmentation was conducted using a
morphological gradient on the CMR-images after
some noise reduction was performed by using the
BIOIMAGING2015-InternationalConferenceonBioimaging
52

Figure 5: Segmentation results from one slice of an example patient. First row, left to right: Original image with manual
markings, a posteriori probability map, gradient from a posteriori probability map. Second row, left to right: epicardium mask
from automatic method used as external marker, true endocardium mask with proposed method in red and WS
PMGepi
in green,
original image with overlaid contours of epicardium (blue) endocardium (proposed method, red) and WS
PMGepi
(green) after
post processing.
morphological center algorithm (Soille, 2003). The
corresponding results are named WS
MG
when the
external marker was the edge of the cropped im-
age, where the cropping was done automatically us-
ing the hear center as input, and WS
MGepi
when the
external marker is defined by the epicardium mask,
Mask
i
epicard
(x). The latter is done since the endo-
cardium border cannot cross the (true) epicardium
border.
Watershed segmentation using the a posteriori
probability map images as input to find the morpho-
logical gradient images was also executed. The re-
sults are named WS
PMG
when the external marker
is the edge of the cropped image, and WS
PMGepi
when the external marker is defined by the epicardium
mask, Mask
i
epicard
(x). Two different internal marker
are tested; the heart center from our proposed au-
tomatic method using the circular Hough Transform
(CHT), see Table 2, and the true heart center, see Ta-
ble 3.
Results from some slices of an example patient are
depicted in Figure 6. For this example patient we can
see that the proposed method performs better than the
depicted WS
MGepi
, since the latter includes more of
the scar in the bloodpool. One slice of another exam-
ple patient is depicted in Figure 5 at different stages
together with the result of the proposed method as
well as WS
PMGepi
. In this example the WS
PMGepi
Table 2: Jaccard and Dice index, averaged over 395 images.
Standard deviation in parentheses. Heart center from auto-
matic method.
Endocard seg. Dice Jaccard
Prop.method 0.85 (0.048) 0.74 (0.070)
WS
MG
0.80 (0.075) 0.68 (0.099)
WS
MGepi
0.83 (0.060) 0.71 (0.084)
WS
PMG
0.78 (0.050) 0.65 (0.068)
WS
PMGepi
0.79 (0.066) 0.65 (0.086)
Table 3: Jaccard and Dice index averaged over 395 images.
True heart center (HC) as input.
Endocard seg. Dice Jaccard
Prop.method 0.87 (0.040) 0.77 (0.062)
WS
MG
0.80 (0.075) 0.68 (0.099)
WS
MGepi
0.84 (0.055) 0.72 (0.080)
WS
PMG
0.80 (0.055) 0.67 (0.075)
WS
PMGepi
0.81 (0.068) 0.69 (0.088)
fails completely whereas the proposed method per-
forms quite well.
SegmentationofLGEnhancedCardiacMRI
53

Figure 6: Segmentation results from some slices of an example patient. First row, white is manual marking, red is result from
proposed method, dice index of this patient is 0.90. Second row, white is manual marking, green is WS
MGepi
, Dice index of
this patient is 0.84.
4 CONCLUSION
The presented method for segmentation of endo-
cardium in LGE-CMR completes a larger system
for automatic segmentation of the myocardium in
LGE-CMR. The proposed system is based on us-
ing some prior information about LGE-CMR images:
the bloodpool and the myocardial muscle is approx-
imately circular and this is used when constructing
an a priori probability map. The 3D information is
utilized both finding the heart center and when pro-
ducing the a posteriori probability map. The CMR
images are not true 3D in the sense that the resolution
in the z-direction (i.e. between slices) is much coarser
then the resolution within a slice.
All experiments are conducted on a dataset of 54
patients, all with myocardial infarctions. Twenty of
these patients are patients implanted with ICD (CMR
images recorded prior to implantation), and these
patients have severe scars, and sometimes enlarged
hearts, making the segmentation even more challeng-
ing.
Results on the endocardium segmentation using
the proposed method was compared to results using
watershed with different gradients and different ex-
ternal markers. The mean Dice and Jaccard of the
proposed fully automatic method are 0.85 and 0.74
respectively. Using the true heart center as input im-
proves the Dice index to 0.87 and the Jaccard index
to 0.77 showing the potential of the latter part of the
proposed system. Watershed gave the corresponding
results 0.8 and 0.68. Using the epicardium segments
from the proposed method as the external marker im-
proved the watershed results, were the best results
gave Dice index 0.83 and Jaccard index 0.71. The
reported results in (Alba et al., 2012) are very good
(Mean Dice index of 0.81 for the myocardial mus-
cle), but on a limited dataset of LGE-CMR images
(20 patients). In future work we will strive to do a fair
comparison of our method with (Alba et al., 2013) .
REFERENCES
Alba, X., i Ventura, R. F., Lekadir, K., and Frangi, A.
(2012). Conical deformable model for myocardial
segmentation in late-enhanced MRI. In Proceed-
ings of IEEE International Symposium on Biomedical
Imaging (ISBI. 10.1109/ISBI.2012.6235536.
Alba, X., i Ventura, R. F., Lekadir, K., Tobon-Gomez,
C., Hoogendoorn, C., and Frangi, A. (2013). Au-
tomatic cardiac lv segmentation in MRI using mod-
ified graph cuts with smoothness and interslice con-
straints. Magnetic Resonance in Medicine. doi:
10.1002/mrm.25079.
Ciofolo, C., Fradkin, M., Mory, B., Hautvast, G., and
Breeuwer, M. (2008). Automatic myocardium seg-
mentation in late-enhancement MRI. In Proceed-
ings of IEEE International Symposium on Biomedical
Imaging (ISBI).
de Bruijne, M. and Nielsen, M. (2004). Shape particle fil-
tering for image segmentation. In Proc. of MICCAI,
volume 3216, pages 168–175.
Dice, L. R. (1945). Measures of the amount of ecologic
BIOIMAGING2015-InternationalConferenceonBioimaging
54

association between species. Ecology, 26(3):297–302.
doi:10.2307/1932409.
Dikici, E., ODonnell, T., Setser, R., and White, R. (2004).
Quantification of delayed enhancement MR images.
In Proceedings of the International Conference on
Medical Image Computing and Computer-Assisted In-
tervention, pages 250–257.
Engan, K., Naranjo, V., Eftestøl, T., Ørn, S., and Woie, L.
(2013a). Automatic segmentation of the epicardium
in late gadolinium enhanced cardiac MR images. In
Proc. of Comp. in Cardiology 2013, Zaragoza, Spain.
Engan, K., Naranjo, V., Eftestøl, T., Woie, L., Schuchter,
A., and Ørn, S. (2013b). Automatic detection of heart
center in late gadolinium enhanced MRI. In Proceed-
ings of MEDICON 2013, Sevilla, Spain.
Heiberg, E., Sjgren, J., Ugander, M., Carlsson, M., Eng-
blom, H., and Arheden, H. (2010). Design and valida-
tion of segment a freely available software for cardio-
vascular image analysis. In BMC Medical Imaging,
volume 10:1.
Impedovo, S., Marangelli, B., and Fanelli, A. M. (1978). A
fourier descriptor set for recognizing nonstylized nu-
merals. IEEE Trans. Sys., Man., Cyber, 8(8):640–645.
doi: 10.1109/TSMC.1978.4310042.
Jaccard, P. (1912). The distribution of the flora in the alpine
zone. New Phytologist, (11):37–50.
Meyer, F. (1994). Topographic distance and watershed
lines. Signal Processing, 38:113–125.
ODonnell, T., Xu, N., Setser, R., and White, R. (2003).
Semi-automatic segmentation of nonviable cardiac
tissue using cine and delayed enhancement magnetic
resonance images. In Proceedings of SPIE 2003, vol-
ume 5031, page 242.
Otsu, N. (1979). A threshold selection method from gray-
level histograms. IEEE Trans. Sys., Man., Cyber,
9(1):62–66. doi:10.1109/TSMC.1979.4310076.
Soille, P. (2003). Morphological Image Analysis. Springer-
Verlag, Berlin Heidelberg, Germany, 2 edition.
Spreeuwers, L. and Breeuwer, M. (2003). Detection of
left ventricular and epi- and endocardial borders using
coupled active contours. In Proc. Comput. Assisted
Radiol. Surg., page 11471152.
Thygesen, K., Alpert, J., White, H., and et.al. (2007). Uni-
versal definition of myocardial infarction. European
Heart Journal, 28(20):2525–2538.
Wei, D., Sun, Y., Chai, P., Low, A., and Ong, S. (2011).
Myocardial segmentation of late gadolinium enhanced
mr images by propagation of contours from cine mr
images. Med Image Comput Comput Assist Interv,
14:428–35.
Wei, D., Sun, Y., Ong, S., Chai, P., Teo, L. I., and Low,
A. F. (2013). Three-dimensional segmentation of the
left ventricle in late gadolinium enhanced mr images
of chronic infarction combining long- and short-axis
information. Medical Image Analysis, 17(6):685–697.
doi:10.1016/j.media.2013.03.001.
SegmentationofLGEnhancedCardiacMRI
55
