Determination of Bifurcation Angles of the Retinal Vascular Tree

through Multiple Orientation Estimation based on Regularized

Morphological Openings

Sandra Morales

1,2

Alvar-Gin

es Legaz-Aparicio

, Valery Naranjo

1,2

and Rafael Verd

u-Monedero

Instituto Interuniversitario de Investigaci

on en Bioingenier

ıa y Tecnolog

ıa Orientada al Ser Humano, Universitat

Polit

ecnica de Val

encia, I3BH/LabHuman, Camino de Vera s/n, 46022 Valencia, Spain

Grupo Tecnolog

ıas de Inform

atica Aplicadas a la Oftalmolog

ıa, Unidad Conjunta UPV- FISABIO, Valencia, Spain

Universidad Polit

ecnica de Cartagena, Cartagena, Spain

Keywords:

Retinal Image, Bifurcation Angle, Multiple Orientation Estimation, Regularized Morphological Opening.

Abstract:

This paper describes a new approach to compute bifurcation angles in retinal images. This approach is based

on the estimation of multiple orientations at each pixel of a gray retinal image. The main orientations are

provided by directional openings whose outputs are regularized in order to extend the orientation information

to the whole image. The detection of vessel bifurcations is based on the coexistence of two or more than two

different main orientations at the same pixel. Once the bifurcations and crossovers has been identiﬁed, bifur-

cation angles are calculated. The proposed procedure of computing bifurcation angles by means of orientation

estimation at all pixels of the gray level image is much more stable than those methods which are based on the

skeleton of the vascular tree, since a slight variation of a pixel of the skeleton can produce a signiﬁcant change

in the angle value.

1 INTRODUCTION

Retinal vasculature is able to indicate the status of

other vessels of the human body. Its study involves

a non-invasive or minimally invasive procedure and,

usually, it is included in the standard screening of

any patient with diseases in which the vessels may be

altered. Speciﬁcally, the identiﬁcation and study of

bifurcations and crossovers has great signiﬁcance in

cardiovascular diseases as well as in their early detec-

tion (Azzopardi and Petkov, 2011). Moreover, vas-

cular changes produced in systemic diseases usually

induce particular modiﬁcations in the vessels, such as

changes in bifurcation angles. Based on this fact, this

paper is focused on automatically determining the bi-

furcation angles calculated on vessel bifurcations pre-

viously detected. There are two approaches to de-

tect vessel bifurcations: methods based on geometri-

cal features and methods based on models (Abramoff

et al., 2010). The method proposed in this paper be-

longs to the ﬁrst group. In particular, the detection of

vessel bifurcations is addressed by analyzing a mul-

tiple orientation vector ﬁeld provided by the regular-

ization of directional morphological openings. The

orientation ﬁeld is given by a directional signature

(Soille and Talbot, 2001) for each pixel using a set

of directional openings with a line segment. Then,

the orientation of a pixel is deﬁned as the one asso-

ciated to the directional opening which produces the

maximum value of the signature of this pixel. Nev-

ertheless, the original approach from (Soille and Tal-

bot, 2001) does not deal with the multiple orientation

case and does not take into account that, locally, pix-

els in natural images can be associated to more than

one orientation, e.g., crossing lines, corners and junc-

tions (also known as X-, L- and Y-junctions, respec-

tively). To determine not only the main direction but

all the signiﬁcant orientations, the directional signa-

ture is analyzed in the present work using multiple

peak detection on the curve interpolated by b-splines.

Thanks to the estimation of the main orientations of

each bifurcation point of the retinal images, the an-

gles generated by the vessels on all of them can be

analyzed.

In the literature, the most common approach to

detect retinal tree bifurcations and their correspond-

ing bifurcation angles is through the analysis of the

segmented vascular tree. In general, this segmenta-

tion can be performed by matched ﬁlters (Chaudhuri

et al., 1989), by region growing and scale-space anal-

126

Morales S., Legaz-Aparicio Á., Naranjo V. and Verdú-Monedero R..

Determination of Bifurcation Angles of the Retinal Vascular Tree through Multiple Orientation Estimation based on Regularized Morphological Openings.

DOI: 10.5220/0005170101260131

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2015), pages 126-131

ISBN: 978-989-758-069-7

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

ysis (Mart

ınez-P

erez et al., 1999), by mathematical

morphology (Zana and Klein, 2001), etc. Regarding

the detection of vessel bifurcations and crossovers on

segmented retinal images it can be done, e.g., by us-

ing a set of trainable keypoint detectors and a bank of

Gabor ﬁlters (Azzopardi and Petkov, 2013), or with

matched ﬁlters (Ardizzone et al., 2008). The mea-

surement of the bifurcation angles is usually carried

out ﬁtting the segmented vessels, or their skeleton, by

straight lines and then estimating the angle between

them (Gao et al., 2000; Martinez Perez et al., 2002;

MacGillivray et al., 2012). Segmentation-dependent

results are the major drawback of this approach: a

slight variation of a pixel in the skeleton results can

produce a signiﬁcant change in the angle value, even

of several degrees.

This paper is organized as follows: Section 2

ﬁrstly addresses the method to estimate multiple ori-

entations at each pixel, and then the approach fol-

lowed to detect the bifurcations and crossovers in reti-

nal images together with the calculation of the bifur-

cation angles is described. Section 3 shows the results

of the proposed method in a public database. Finally,

Section 4 closes the paper with the conclusions and

future work lines.

2 METHOD

The goal of this paper is to propose a new method

to compute bifurcation angles of the retinal tree from

a gray image without resorting to the skeletonization

of a segmented (binary) image. For that purpose,

three stages are necessary: estimation of the multi-

ple orientation vector ﬁeld, detection of bifurcations

and crossovers and, ﬁnally, the measurement of the

desired angles. The key of the method is the way to

estimate the multiple orientations existing in a fundus

image. The algorithm proposed to carried out this es-

timation is depicted in Figure 1. This approach differs

from (Angulo et al., 2011), where the multiple main

orientations are estimated by analysing a block of the

image, whereas in this paper the multiple orientations

are estimated at each pixel.









k∇k

















































˜g









Multiple

peak

Figure 1: Flowchart of the multiple orientation estimation

method.

2.1 Multiple Orientation Estimation

Let f (x) : E → R be a gray-level image, where the

support space is E ⊂ Z

and the pixel coordinates are

x = (x,y). Let us deﬁne g(x) as the absolute value of

the gradient of f (x), i.e.,

g(x) = k∇ f (x)k =



∂ f (x,y)

∂x





∂ f (x,y)

∂y



. (1)

The directional opening of g(x) by a linear (sym-

metric) structuring element (SE) of length l and direc-

tion θ is deﬁned as the directional erosion of g by L

θ,l

followed by the directional dilation with the same SE

(Verd

u-Monedero et al., 2011):

θ,l

(g)(x) = δ

θ,l

[ε

θ,l

(g)](x), (2)

where the directional erosion and dilation are respec-

tively

θ,l

( f )(x) =

h∈L

θ,l

(x)

{

f (x + h)

}

, (3)

θ,l

( f )(x) =

h∈L

θ,l

(x)

{

f (x − h)

}

. (4)

The proposed orientation model is based on a de-

composition of the gradient information by families

of linear openings, {γ

}

i∈I

, according to a particu-

lar discretization of the orientation space {θ

}

i∈I

In the next step of the proposed method, a ﬁltering

is performed at each one of the directional openings

(depicted as H

in Figure 1). The ﬁltering diffuses the

orientation information and avoids angle mismatches

due to noise. The kernel H

is the sampling of the

gaussian low-pass ﬁlter

(ω

,ω

) = e

−

(ω

+ω

)

, (5)

where σ is the spatial standard deviation of the ﬁlter.

More details of the method can be found in (Legaz-

Aparicio et al., 2014).

Once the directional openings have been ﬁltered,

the directional signature at pixel x is deﬁned as

x;l

(i) = ˜g

(x). (6)

Then, s

x;l

(i) is interpolated using cubic b-splines and

its maxima correspond to the multiple orientations ex-

isting at pixel x. Finally, collecting all the orientations

estimated at all the pixels in the image provides the

multidimensional vector ﬁeld

θ(x).

2.2 Detection of Bifurcations and

Crossovers

The method previously presented can be applied to

a gray or on a binary image. The resulting orienta-

tion vector ﬁeld can be used then to detect the ex-

isting bifurcations and crossovers of the retinal tree

DeterminationofBifurcationAnglesoftheRetinalVascularTreethroughMultipleOrientationEstimationbasedon

RegularizedMorphologicalOpenings

127

(see Figure 2). In general, most of the methods which

detect signiﬁcant points of a vascular tree are based

on a previously segmented, and therefore binary, im-

age. In this paper, the segmentation stage is skipped

and the method is applied directly to a gray image,

avoiding the segmentation result dependence. How-

ever, the method can also be applied to a segmented

image, providing a better orientation ﬁeld due to the

binarization of the image.

Figure 2: Left: real retinal image. Right: close-up of the

image with its estimated multiple orientation vector ﬁeld.

The detection procedure takes into account only

the two main orientations at each pixel. The method

considers that a bifurcation or crossover exists if two

conditions happen. The ﬁrst condition is that the mag-

nitude of the regularized opening has to be greater

than a threshold, | ˜g

| > th. The second condition to

be fulﬁlled is that the two main orientations must dif-

fer more than 2∆θ, where ∆θ is the angular resolution

of the multiple orientation estimation method. After

processing these two conditions, a reﬁnement stage

is necessary to reduce false positives and then to dis-

criminate between bifurcations or crossings and high

curvature areas.

2.3 Classiﬁcation of Detected Points

In order to determine which interest points are bifur-

cations and crossovers and which ones are high cur-

vature areas, a control area around each point of inter-

est is established. The control area is a window with

circular shape centred in the point of interest. The ra-

dius of the window must be large enough to contain

the vessels belonging to the point of interest. At this

stage, a coarse segmentation based on a top-hat mor-

phological ﬁlter followed by a threshold is performed.

The aim of this segmentation is to speed up the clas-

siﬁcation stage.

The classiﬁcation is carried out by placing a cir-

cular window at the interest point and analyzing the

number of branches that cross the circle deﬁned by

the mask. According to the number of branches that

cross the circle, the points of interest are classiﬁed

(a) (b) (c) (d)

Figure 3: Circular windows placed at different detected in-

terest points with two main orientations.

into four types:

• If there is only one branch, the point of interest is

a vessel termination (see Figure 3(a)).

• If there are two branches, the point of interest is a

vessel with high curvature (see Figure 3(b)).

• If there are three branches (in general, an odd

number greater than one), the point of interest will

be a bifurcation (see Figure 3(c)).

• Finally, if there are four branches (in general, an

even number greater than two), the point of inter-

est will be a crossover (see Figure 3(d)).

Since we are interested in detecting bifurcations and

crossovers, only the points of interest whose mask

is crossed by more than two branches will be con-

sidered. Figure 4(a)-(b) show the detected interest

points and Figure 4(c)-(d) show the bifurcations and

crossover after the classiﬁcation stage.

(a) (b)

Figure 4: (a) Detection of interest points: bifurcations,

crossings and high curvature areas. (b) Close-up of (a). (c)

Bifurcations after the classiﬁcation. (d) Close-up of (c).

BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

128

2.4 Measurement of Bifurcation Angles

Once the bifurcations have been classiﬁed, it is pos-

sible to measure the bifurcation angles. The angle is

calculated by performing the difference between the

orientation vectors of each branch. From the intersec-

tion of the circular window and the branch, an inte-

rior point is chosen as representative of this branch,

and its orientation vector will deﬁne the orientation

of the branch at this pixel. Note that the choice of

this pixel is not critical since the orientation vector

ﬁeld varies slowly inside the vessel. Due to the dis-

cretization of the orientation space of the multiple ori-

entation method, the orientation is estimated using the

ASGVF method (Verd

u-Monedero et al., 2011) which

achieves a higher angular resolution. Since the AS-

GVF method only estimates the orientation and it is

deﬁned between −90

◦

and 90

◦

degrees, the direction

of each vector can be obtained taking into account the

location of the representative pixel of each branch in

relation to the centre of the bifurcation. Considering

the quadrant of the representative pixel, the direction

of the vector can be obtained, providing a vector ﬁeld

which is deﬁned between 0

◦

and 360

◦

degrees.

Finally, after the conversion of the orientation

space, it is possible to calculate the angular difference

between the vessels contained in the window and thus

to obtain a measure of the bifurcation angle.

3 RESULTS

The performance of the proposed method has been

evaluated on images belonging to DRIVE database

(Staal et al., 2004). This database contains 40 reti-

nal images of 565 × 584 pixels as well as their man-

ual segmentation performed by experts. DRIVE is

often used to evaluate segmentation algorithms de-

signed speciﬁcally for the retinal vascular tree. In

this paper, two methods for the computation of bi-

furcation angles have been compared: the proposed

method based on the orientation vector ﬁeld and the

method described in (Morales et al., 2014).

Regarding the proposed method, it has been ap-

plied directly to the green component of the origi-

nal RGB image. The directional openings were per-

formed using an oriented linear structuring element

of 7 pixels. This length comes from the trade-off be-

tween the curvature of the vessels and the angular res-

olution of the structuring element (it provides ∆θ =

◦

and produces a ﬁlter bank with 12 branches). The

low-pass ﬁltering of the directional openings is per-

formed using σ=1. The threshold th used to consider

that a pixel belongs to a bifurcation or crossover is the

25% of the maximum intensity value. In Figure 5, the

angles measured on two images of DRIVE database

can be observed. Only a region of interest of these

images has been shown for better visualization.

The parameters of the orientation estimation have

been chosen to deal with this particular resolution.

However, the orientation estimation method can be

improved by considering a multiscale approach as de-

scribed in (Angulo et al., 2011). There, the estimation

of the orientation properties is provided by directional

openings by line segments of variable length, which

produce directional signatures for various scales.

With respect to the algorithm presented in

(Morales et al., 2014), the main difference is that it

only can be applied to binary images. Moreover, once

the vessels have been segmented with this approach,

the retinal vascular tree must be labelled in order to

perform the angle measurements. The vascular tree

labelling is focused on obtaining the vascular skele-

ton, detecting its bifurcation points through hit-or-

miss transformations and a tracking process. Then,

the angle formed by the daughter branches of each bi-

furcation point is calculated. The branches are ﬁtted

by straight lines using least-squares in a circular win-

dow centred on these points. As it was mentioned in

Section 1, the main drawback of the methods based

on the vascular skeleton is its excessive dependence

between the skeleton pixels and the measured angle.

Figure 6 shows the measured angles provided by the

method described in (Morales et al., 2014) on differ-

ent expert hand-made segmentations.

Comparing the results shown in Figure 6, it can

be appreciated that the measured angles can be quite

different, reaching a maximum angle variation on the

same image of around 7% in the Figure 6a and around

6% in the Figure 6b. Note that the variation is due to

the fact that the ﬁtted line of the branches depends

directly on the skeleton pixels considered, and the

skeleton shape depends on the segmentation. Only

the change in one pixel of the skeleton can modify the

ﬁtted line and therefore the calculated angle. The an-

gles shown in the Figure 6a and 6b correspond with

the existing bifurcations within the red rectangles of

the Figure 5a and 5b respectively. Since the method

proposed in this paper is based on the grey image and

therefore, it avoids the segmentation and skeletoniza-

tion stages, the provided measurements are much

more accurate, stable and faithful to reality.

4 CONCLUSIONS

This paper has addressed a novel method to measure

bifurcation angles in retinal images. The method is

DeterminationofBifurcationAnglesoftheRetinalVascularTreethroughMultipleOrientationEstimationbasedon

RegularizedMorphologicalOpenings

129

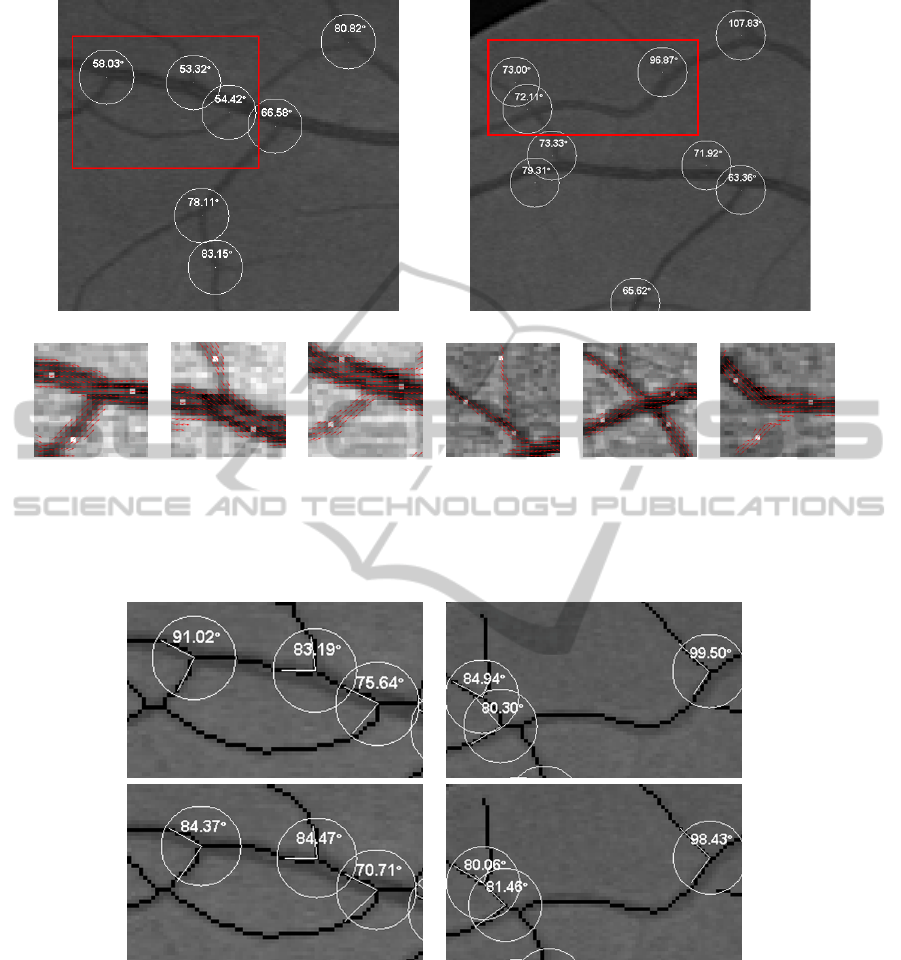
(a) (b)

Figure 5: Angles of the bifurcations with the ASGVF orientation vector ﬁeld on two images from DRIVE database. (a) A

region of interest of the ‘19 test’ image. (b) A region of interest of the ‘40 training’ image. (c)-(e) Close up of selected

bifurcations marked in red in (a). (f)-(h) Close up of selected bifurcations marked in red in (b). The bright pixels inside the

vessels indicate at what points the value of the vector ﬁeld has been taken.

(a) (b)

Figure 6: Bifurcation angles provided by the method described in (Morales et al., 2014) on the selected bifurcations of the

Figure 5. This method is based on the skeletonization of a segmented (binary) image. (a) Skeletonization of two different

expert segmentations of the ‘19 test’ image. (b) Skeletonization of of two different expert segmentations of the ‘40 training’

image. Slight differences in the skeleton cause large differences in the measured angles.

based on a multiple orientation vector ﬁeld which is

obtained from gray images. The coexistence at some

locations of two or more orientations provides the in-

terest points where a bifurcation can exist, but also

high curvature vessels are wrongly provided. After

a classiﬁcation stage, the false positives are reduced

and then the measurement is performed using the ori-

entation estimation provided by the ASGVF of the

gray image. Since the orientation method is based

on the gradient of the gray image, no segmentation

is required. The proposed method can measure ac-

curately the bifurcation angles and it is more robust

BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

130

than other methods which use the skeleton of the seg-

mented image. The measurements based on the skele-

ton depends highly on this process. The change of a

single pixel of the skeleton can modify the line which

ﬁts the branch and therefore it involves variations in

the angle measurement.

As future work, we will evaluate the performance

of the proposed method on all retinal images from

DRIVE (Staal et al., 2004) and STARE (Hoover et al.,

2000) databases. Comparisons with other state-of-art

methods will also be done.

ACKNOWLEDGEMENTS

This work was supported by Ministerio de Econom

ıa

y Competitividad of Spain, Project ACRIMA

(TIN2013-46751-R).

REFERENCES

Abramoff, M., Garvin, M., and Sonka, M. (2010). Retinal

imaging and image analysis. Biomedical Engineering,

IEEE Reviews in, 3:169–208.

Angulo, J., Verd

u-Monedero, R., and Morales-S

anchez, J.

(2011). Multiscale local multiple orientation estima-

tion using Mathematical Morphology and B-spline in-

terpolation. Proc. of 7th Int. Symposium on Image and

Signal Processing and Analysis (ISPA), pages 575 –

578.

Ardizzone, E., Pirrone, R., Gambino, O., and Radosta, S.

(2008). Blood vessels and feature points detection on

retinal images. Engineering in Medicine and Biology

Society, 2008. EMBS 2008. 30th Annual International

Conference of the IEEE, pages 2246–2249.

Azzopardi, G. and Petkov, N. (2011). Detection of reti-

nal vascular bifurcations by trainable v4-like ﬁlters.

CAIP’11 Proc. 14th Int. Conf. on Computer Analysis

of Images and Patterns, 1:451–459.

Azzopardi, G. and Petkov, N. (2013). Automatic detection

of vascular bifurcations in segmented retinal images

using trainable cosﬁre ﬁlters. In Pattern Recognition

Letters, volume 34, pages 922–933.

Chaudhuri, S., Chatterjee, S., Katz, N., Nelson, M., and

Goldbaum, M. (1989). Detection of blood vessels in

retinal images using two-dimensional matched ﬁlters.

IEEE Trans. on Medical Imaging, 8:263–269.

Gao, X. W., Bharath, A., Stanton, A., Hughes, A., Chap-

man, N., and Thom, S. (2000). Quantiﬁcation

and characterisation of arteries in retinal images.

Computer Methods and Programs in Biomedicine,

63(2):133 – 146.

Hoover, A., Kouznetsova, V., and Goldbaum, M. (2000).

Locating blood vessels in retinal images by piecewise

threshold probing of a matched ﬁlter response. IEEE

Transactions on Medical Imaging, 19(3):203–210.

Legaz-Aparicio, A. G., Verd

u-Monedero, R., Morales-

anchez, J., Larrey-Ruiz, J., and Angulo, J. (2014).

Detection of retinal vessel bifurcations by means of

multiple orientation estimation based on regularized

morphological openings. In XIII Mediterranean Con-

ference on Medical and Biological Engineering and

Computing 2013, volume 41 of IFMBE Proceedings,

pages 317–320. Springer International Publishing.

MacGillivray, T., Perez-Rovira, A., Trucco, E., Chin, K.,

Giachetti, A., Lupascu, C., Tegolo, D., Wilson, P.,

Doney, R., Laude, A., and Dhillon, B. (2012). VAM-

PIRE: Vessel Assessment and Measurement Platform

for Images of the Retina. CRC Press.

Martinez Perez, M., Highes, A., Stanton, A., Thorn, S.,

Chapman, N., Bharath, A., and Parker, K. (2002).

Retinal vascular tree morphology: a semi-automatic

quantiﬁcation. IEEE Trans. on Biomedical Engineer-

ing, 49(8):912–917.

Mart

ınez-P

erez, M. E., Hughes, A., Stanton, A., Thom, S.,

Bharath, A., and Parker, K. (1999). Scale-space anal-

ysis for the characterisation of retinal blood vessels.

Medical Image Computing and Computer-Assisted In-

tervention, pages 90–97.

Morales, S., Naranjo, V., L

opez-Mir, F., Navea, A., and niz,

M. A. (2014). Computer-assisted system for hyper-

tensive risk determination through fundus image pro-

cessing. In Romero, L. M. R., editor, XIII Mediter-

ranean Conference on Medical and Biological Engi-

neering and Computing 2013, volume 41 of IFMBE

Proceedings, pages 273–276. Springer.

Soille, P. and Talbot, H. (2001). Directional morphological

ﬁltering. IEEE Trans. on Pattern Analysis and Ma-

chine Intelligence, 23(11):1313–1329.

Staal, J., Abramoff, M., Niemeijer, M., Viergever, M., and

van Ginneken, B. (2004). Ridge-based vessel segmen-

tation in color images of the retina. Medical Imaging,

IEEE Transactions on, 23(4):501–509.

Verd

u-Monedero, R., Angulo, J., and Serra, J. (2011).

Anisotropic morphological ﬁlters with spatially-

variant structuring elements based on image-

dependent gradient ﬁelds. IEEE Trans. Image

Processing, 20(1):200–212.

Zana, F. and Klein, J.-C. (2001). Segmentation of vessel-

like patterns using mathematical morphology and cur-

vature evaluation. IEEE Trans. on Image Processing,

10(7):1010–1019.

DeterminationofBifurcationAnglesoftheRetinalVascularTreethroughMultipleOrientationEstimationbasedon

RegularizedMorphologicalOpenings

131