Automated Cryptanalysis of Bloom Filter Encryptions of Health Records
Martin Kroll and Simone Steinmetzer
Research Methodology Group, University of Duisburg-Essen, Essen, Germany
Keywords:
Bloom Filter, Privacy-preserving Record Linkage, Anonymity, Hash Function, Cryptographic Attack.
Abstract:
Privacy-preserving record linkage with Bloom filters has become increasingly popular in medical applications,
since Bloom filters allow for probabilistic linkage of sensitive personal data. However, since evidence indi-
cates that Bloom filters lack sufficiently high security where strong security guarantees are required, several
suggestions for their improvement have been made in literature. One of those improvements proposes the
storage of several identifiers in one single Bloom filter. In this paper we present an automated cryptanalysis of
this Bloom filter variant. The three steps of this procedure constitute our main contributions: (1) a new method
for the detection of Bloom filter encrytions of bigrams (so-called atoms), (2) the use of an optimization algo-
rithm for the assignment of atoms to bigrams, (3) the reconstruction of the original attribute values by linkage
against bigram sets obtained from lists of frequent attribute values in the underlying population. To sum up,
our attack provides the first convincing attack on Bloom filter encryptions of records built from more than one
identifier.
1 INTRODUCTION
Record linkage between databases containing infor-
mation on individual people is popular in a large num-
ber of medical applications, for example the iden-
tification of patient deaths (Jones et al., 2005), the
evaluation of disease treatment (Newman and Brown,
1997) and the linkage of cancer registries in epidemi-
ology (Van Den Brandt et al., 1990). In many ap-
plications data sets are merged using personal iden-
tifiers such as forenames, surnames, place and date
of birth. Due to privacy concerns this has to be done
via privacy-preserving record linkage (PPRL). How-
ever, since personal identifiers often contain typing or
spelling errors, encrypting the identifier values and
linking only those that match exactly does not pro-
vide satisfactory results. Therefore, to allow for errors
in encrypted personal identifiers, in many European
countries encrypted phonetic codes, such as Soundex
codes, are commonly used, especially by cancer reg-
istries. As the performance of these codes is still non
satisfactory, several novel privacy-preserving record
linkage methods have been suggested during the last
years. For example Schnell et al. (Schnell et al., 2009)
developed a method based on Bloom filters. Bloom-
filter-based record linkage has already been used in
medical applications in a number of different coun-
tries (Kuehni et al., 2012; Rocha, 2013; Randall et al.,
2014; Schnell et al., 2014).
Another frequently applied privacy-preserving
record linkage method uses anonymous linking codes
(Herzog et al., 2007). The basic principle of an anony-
mous linking code is to standardize all particular iden-
tifiers of a record (removal of certain characters and
diacritics, use of upper case letters), to concatenate
them to a single string and finally to put this sin-
gle string into a cryptographic hash function. By
combining this principle with Bloom filters, Schnell
et al. (Schnell et al., 2011) first developed a novel
error-tolerant anonymous linking code, called Crypto-
graphic Longterm Key (CLK). Instead of encrypting
every single identifier from a record of several iden-
tifiers through a Bloom filter, multiple identifiers are
stored in one single Bloom filter, called CLK. Tests on
several databases showed that CLKs yield good link-
age properties, superior to well-known anonymous
linking codes (Schnell et al., 2011).
Only recently Randall et al. (Randall et al., 2014)
presented a study on 26 million records of hospital
admissions data and showed that privacy-preserving
record linkage with Bloom filters built from multiple
identifiers is applicable to large real-world databases
without loss in linkage quality.
However, only little research on the security of
Bloom filters built from more than one identifier
has yet been published (see subsection 2.2). In
several countries, this lack of research prevents the
widespread use of Bloom filter encryptions for real-
5
Kroll M. and Steinmetzer S..
Automated Cryptanalysis of Bloom Filter Encryptions of Health Records.
DOI: 10.5220/0005176000050013
In Proceedings of the International Conference on Health Informatics (HEALTHINF-2015), pages 5-13
ISBN: 978-989-758-068-0
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

world medical databases (such as cancer registries)
where the anonymity of the individuals has to be guar-
anteed. For example, in its Beyond 2011 Programme
the British Office for National Statistics investigated
several methods for linking sensitive data sets (Office
for National Statistics, 2013). The investigators came
to the conclusion that none of the “(...) recent inno-
vations, such as bloom filter encryption (...)” can be
recommended because they “(...) have not been fully
explored from an accreditation perspective”. Thus,
research showing drawbacks of the recent Bloom fil-
ter techniques is important because it guides the di-
rection for future research and might motivate further
development of the recent procedures. In this paper,
we intend to investigate this issue in detail by giving
the first convincing cryptanalysis of Bloom filter en-
cryptions built from more than one identifier.
2 BACKGROUND
In 1970, Burton Howard Bloom (Bloom, 1970) intro-
duced a novel approach that permits the efficient test-
ing of set membership through a probabilistic space-
efficient data structure. A Bloom filter is a bit array of
length L, which at first contains zeros only. Let S ⊆ U
be a subset of a universe U. Then S can be stored in a
Bloom filter B = B(S) = (b
0
,. .. ,b
L−1
) in the follow-
ing way: Each element s ∈ S is mapped via k different
hash functions h
0
,. .. ,h
k−1
: S −→ {0,...,L − 1} and
all the corresponding bit positions b
h
0
(s)
,. .. ,b
h
k−1
(s)
are set to one. Once a bit position is set to one this
value no longer changes.
Furthermore, to test whether an item u ∈ U from
the universe is contained in S, u is hashed through the
k hash functions h
0
,. .. ,h
k−1
as well. Consequently,
if all bit positions b
h
0
(u)
,. .. ,b
h
k−1
(u)
in the Bloom fil-
ter are set to one, then u ∈ S holds with high proba-
bility. However, false positive values can occur when
the ones on positions h
0
(u),. .. ,h
k−1
(u) are caused by
two or more different elements from S. Then the test
indicates u ∈ S although this is not the case. Other-
wise, if at least one bit position in the two Bloom fil-
ters varies, u clearly is no member of S.
2.1 PPRL with Bloom Filters Built from
Multiple Identifiers
In (Schnell et al., 2009) Bloom filters were used
in privacy-preserving record linkage for the first
time. This approach was expanded to Cryptographic
Longterm Keys in (Schnell et al., 2011).
In common PPRL protocols two data owners A
and B agree on a set of identifiers that occur in both
of their databases. Next, these identifiers are stan-
dardized, then padded with blanks at the beginning
and the end, and finally split into substrings of two
characters. Each substring of the first identifier corre-
sponding to a record is mapped to the first Bloom fil-
ter via several hash functions. Afterwards, each sub-
string of the second identifier, corresponding to the
same record, is mapped through another set of hash
functions to the first Bloom filter as well. This proce-
dure is repeated until all identifiers of the first record
are stored in the first Bloom filter. Next, all identifiers
corresponding to the second record of the database
are mapped through the utilized hash functions to a
second Bloom filter and so on. Performing this pro-
cedure for all entries of the database results in a set
of Bloom filters where each Bloom filter is built from
multiple identifiers. Thus, the similarity of the Bloom
filters is a measure for the similarity of the encoded
identifiers. Usually, the linkage of the two databases
is conducted by a third party C.
Because of the specific structure of Bloom filters,
record linkage based on Bloom filters built from mul-
tiple identifiers allows for errors in the encrypted data.
Therefore, they can be applied to linking large data
sets such as national medical databases (Randall et al.,
2014).
2.2 Extant Research: Attacks on Bloom
Filters of One or More Identifiers
To the best of our knowledge, only two ways of at-
tacking Bloom filters of one identifier and one way
of attacking Bloom filters of multiple identifiers are
known so far.
The first cryptanalysis of Bloom filters was pub-
lished in 2011. Kuzu et al. (Kuzu et al., 2011) sam-
pled 20,000 records from a voter registration list and
encrypted the substrings of two characters from the
forenames through 15 hash functions and Bloom fil-
ters of length 500 bits. Their attack consisted in solv-
ing a constraint satisfaction problem (CSP). Through
a frequency analysis of the fornames and the Bloom
filters and by applying their CSP solver to the prob-
lem, Kuzu et al. were able to decipher approximately
11% of the data.
In contrast, Niedermeyer et al. (Niedermeyer
et al., 2014) proposed an attack on 10,000 Bloom fil-
ters built from encrypted German surnames that were
considered to be a random sample of a known popu-
lation. For the generation of the Bloom filters 15 hash
functions and Bloom filter length 1,000 were used.
Then they conducted a manual attack based on the fre-
quencies of the substrings of length two, which they
derived from the German surnames. Thus, Nieder-
HEALTHINF2015-InternationalConferenceonHealthInformatics
6

meyer et al. deciphered the 934 most frequent sur-
names of 7,580 different ones, which corresponds to
approximately 12% of the data set. However, their
attack is not limited to the most frequent names and
could be extended to the decipherment of nearly all
names.
In 2012 Kuzu et al. (Kuzu et al., 2012) showed
an attack on Bloom filters built from multiple identi-
fiers. They applied their constraint solver to forename
and surname, as well as forename, surname, city and
ZIP code, of 50,000 randomly selected records from
the North Carolina voter registration list. However,
they were not able to mount a successful attack. Thus,
Kuzu et al. supposed that combining multiple per-
sonal identifiers into a single Bloom filter would of-
fer a protection mechanism against frequency attacks.
Although they suspected that their attack did not un-
cover all vulnerabilities of the Bloom filter encodings,
they showed that the CSP for multiple identifiers is in-
tractable to solve by their constraint solver.
2.3 Our Contribution
In this paper we present a fully automated attack on a
database containing forenames, surnames and the rel-
evant place of birth as well. All records are considered
to be a random sample of a known population. We
suppose that the attacker only knows some publicly
available lists of the most common forenames, sur-
names and locations. The attack is based on analyzing
the frequencies and the combined occurence of sub-
strings of length two from the identifiers of these lists.
Furthermore, we are interested in recovering as many
identifiers as possible. Our cryptanalysis was imple-
mented using the programming languages Python and
C++.
3 ENCRYPTION
In this section some basic notation is introduced and
the encrypting procedure is described.
In record linkage scenarios, strings are usually
standardized through transformations such as capital-
ization of characters or removal of diacritics (Randall
et al., 2013). After this preprocessing step all strings
contain only tokens from some predefined alphabet Σ.
Throughout this article, we use the canonical alpha-
bet Σ := {A,B,...,Z,
}, where denotes the padding
blank. Thus, for example the popular German sur-
name M
¨
uller is transformed to MUELLER in the pre-
processing step. As usual, we denote substrings of
two characters with bigrams and the set containing
all the bigrams with Σ
2
, i.e.
Σ
2
= { , A,..., Z,A ,...,Z ,AA,...,ZZ}.
The Bloom filter encryption of a record from a
database is created by storing the bigram set associ-
ated with this record into a Bloom filter. The bigram
set associated with a record is defined as the set con-
taining the bigrams from all the identifiers. Here, a
distinction between the bigrams occuring in different
identifiers is made. Thus, if the set of identifiers is
denoted with I , the bigram set of a record is a subset
of I × Σ
2
.
For example, if we have I = {surname,forename}
and the database contains a record, Peter M
¨
uller,
the bigram set S
record
associated with this record
would contain the bigrams P
f
, PE
f
, ET
f
, TE
f
, ER
f
,
R
f
, M
s
, MU
s
, UE
s
, EL
s
, LL
s
, LE
s
, ER
s
and R
s
(the sub-
script f indicates the bigrams occuring in the fore-
name identifier, the subscript s the ones occuring in
the surname identifier).
Next, this bigram set is stored into a Bloom filter
(b
0
,. .. ,b
L−1
) of length L by means of k independent
hash functions
h
i
: I × Σ
2
→ {0, .. ., L − 1}
for i = 0,. .. ,k −1. In practice, one could alternatively
use different hash functions h
i
: Σ
2
→ {0,...,L − 1}
for the distinct identifiers in order to guarantee that the
hash values for distinct identifiers are not the same.
Further, as in (Niedermeyer et al., 2014) we in-
troduce the term atom for the specific Bloom filters
which occur as the fundamental building blocks of the
encryption method.
Definition 3.1 (Atom). Let L,k ∈ N and some hash
functions h
0
,. .. ,h
k−1
be defined as above. Then, a
Bloom filter
B := (b
0
,. .. ,b
L−1
) ∈ {0, 1}
L
is termed an atom if there exists a bigram β ∈ I × Σ
2
such that b
j
= 1 ⇔ h
i
(β) = j for some i = 0,...,k−1.
Such a Bloom filter is called the atom realized by the
bigram β and denoted with B(β).
Thus, atoms are special Bloom filters. Since each
bigram is hashed via each h
i
for i = 0,...,k − 1, at
most k positions in an atom can be set to one.
By combining the atoms of the underlying bigram
set of a record with the bitwise OR operation, the
Bloom filter of a record is composed as
B(record) =
_
β∈S
record
B(β),
where
W
denotes the bitwise OR operator.
Note that the same bigram from Σ
2
is hashed dif-
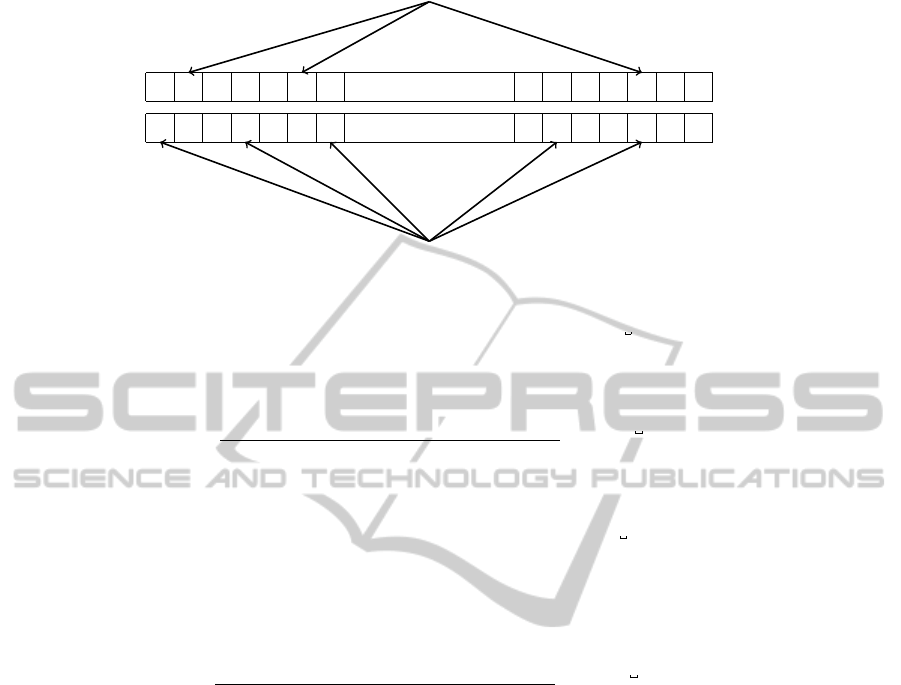
ferently if it occurs in distinct identifiers. This is il-
lustrated in Figure 1 for the example of the bigram ER
AutomatedCryptanalysisofBloomFilterEncryptionsofHealthRecords
7

ER
f
h
1
h
0
h
2
. . .
0 0
1
0 0 0
1
0
. . .
0 0 0 0
1
0 0
999
ER
s
. . .
h
2
h
3
h
4
h
0
h
1
0
1
0 0
1
0 0
1
. . .
0
1
0 0
1
0 0
999
Figure 1: Two different atoms of the bigram ER. These atoms are realized when instances of ER occur in distinct identifiers.
0000100000. .. 0000000010 B( P
f
)
∨ 0001000001. .. 0100000100 B(PE
f
)
∨ 0101010101. .. 0001010101 B(ET
f
)
∨ 0001000010. .. 0001000010 B(TE
f
)
∨ 0100010001. .. 0000000100 B(ER
f
)
∨ 0101010101. .. 0000000001 B(R
f
)
0101110111. .. 0101010111 B(Peter)
0000000100. .. 0000000001 B( M
s
)
∨ 0010000000. .. 0100000000 B(MU
s
)
∨ 0000100000. .. 0010000010 B(UE
s
)
∨ 1000000010. .. 0010000000 B(EL
s
)
∨ 0100001000. .. 0100001000 B(LL
s
)
∨ 1000000100. .. 0001000000 B(LE
s
)
∨ 1001001001. .. 0000100100 B(ER
s
)
∨ 0010001000. .. 0000000010 B(R
s
)
1111101111. .. 0111101111 B(M
¨
uller)
Figure 2: Bloom filters of the forename Peter and the surname M
¨
uller, composed of the atoms belonging to the underlying
bigrams.
which occurs in the record Peter M
¨
uller both in the
surname and the forename identifier.
Mapping each bigram of the forename Peter with
k hash functions results in six atoms; for the sur-
name M
¨
uller, we get eight atoms. Thus, the separate
Bloom filters for these identifiers might be composed
as illustrated in Figure 2.
The final Bloom filter for the record Peter
M
¨
uller is composed by appling the bitwise OR op-
eration to the separate Bloom filter encryptions of the
distinct identifiers. This is demonstrated in Figure 3.
In practice, the Bloom filter encryption of a record
might contain a mixture of string valued identifiers
(such as forename, surname or place of birth) and
also numerical identifiers, such as date of birth. How-
ever, in this paper we restrict ourselves to the case of
string valued attributes only, albeit our cryptanalysis
proposed below is not limited to such attributes.
Assumptions
In many record linkage scenarios, it is supposed that
a semi-trusted third party conducts the record link-
age between two encrypted databases. In this paper
we assume a data set containing Bloom filters built
from multiple identifiers that is sent to a semi-trusted
third party. This third party acts as the adversary and
tries to infer as much information as possible from
the record encryptions. We further suppose that the
attacker has knowledge of the encryption process.
For our scenario we generated 100,000 Bloom fil-
ters built from standardized German forenames, sur-
names and cities according to the distribution in the
population. The identifiers were truncated after the
tenth letter, padded with blanks, respectively, and
were broken into bigrams. Then the bigrams were
hashed through k = 20 hash functions into Bloom fil-
HEALTHINF2015-InternationalConferenceonHealthInformatics
8

0101110111. .. 0101010111 B(Peter)
∨ 1111101111. .. 0111101111 B(M
¨
uller)
1111111111. .. 0111111111 B(entire record)
Figure 3: The Bloom filter of the record Peter M
¨
uller is obtained by applying the bitwise OR operation to the Bloom filter
encryptions of the separate identifiers.
ters of length L = 1, 000. As proposed in (Schnell
et al., 2009) and (Schnell et al., 2011), we used the so-
called double hashing scheme for the generation of k
hash functions from two hash functions f and g. This
double hashing scheme is defined via the equation
h
i
= ( f + i · g) mod L for i = 0, .. ., k − 1 (1)
and was originally proposed in (Kirsch and Mitzen-
macher, 2008) as a simple hashing method for Bloom
filters yielding satisfactory performance results.
In our cryptanalysis we assume that the adversary
knows that the hash values are generated in accor-
dance with equation (1). It is self-evident that s/he
must not have direct access to the hash functions f
and g since this would permit the adversary to check
whether a specific bigram is contained in a given
Bloom filter.
Note that the double hashing scheme has also been
used for the generation of Bloom filters by Kuzu et
al. (Kuzu et al., 2012). However, in that paper the
knowledge of the double hashing scheme was not ex-
ploited in their cryptanalysis.
4 CRYPTANALYSIS
This section provides a detailed description of the de-
ciphering process. At first we try to detect the atoms
that are contained in the given Bloom filters. Then,
we assign bigrams to these atoms by means of an op-
timization algorithm. Finally, the original attributes
are reconstructed from the atoms.
Our approach for the development of a fully auto-
mated attack is based on previous results on the au-
tomated cryptanalysis of simple substitution ciphers
presented by Jakobsen (Jakobsen, 1995). We give a
short account of Jakobsen’s results in order to moti-
vate our procedure.
4.1 Automated Cryptanalysis of Simple
Substitution Ciphers
The encryption of a plaintext message through a sim-
ple substitution cipher is defined by a permutation of
the underlying alphabet Σ. For instance, the message
HELLO LISBON with tokens from the alphabet
Σ = { ,A,B,...,Z} could be encrypted as
RVUUYJUOWAYL.
It is well known that this kind of encryption can be
broken easily by means of a frequency analysis. How-
ever, just replacing the i-th frequent character in the
ciphertext with the i-th frequent character in the un-
derlying language will usually not lead to the cor-
rect decipherment (even for longer messages). This
is commonly compensated for by taking bigram fre-
quencies into consideration as well.
The expected bigram frequencies can be obtained
from a training data set composed of the underlying
language and stored in a quadratic matrix E (in the
above example a 27 × 27 matrix), where the entry e
i j
is equal to the relative proportion of the bigram c
i
c
j
in
the training text corpus and c
i
denotes the i-th charac-
ter of the alphabet. Analogously, the bigram frequen-
cies of the ciphertext can be stored in a matrix D.
The algorithm proposed by Jakobsen (Jakobsen,
1995) was intended to find a permutation σ
opt
of the
alphabet such that the objective function f defined via
f (σ) :=
∑
i, j
|d
σ(i)σ( j)
− e
i j
| (2)
was minimized. The algorithm starts with the initial
permutation that reflects the best assignment between
single characters in the plaintext and the ciphertext
with respect to their relative frequency. In each step of
the algorithm two elements of the currently best per-
mutation σ
opt
are swapped, leading to a new candidate
permutation σ. If f (σ) < f (σ
opt
) holds, the current
permutation is updated to σ, otherwise σ is discarded
and a new candidate σ is generated by swapping two
other elements of σ
opt
. This is repeated until no swap
leads to a further improvement of the objective func-
tion f . Throughout this paper we use the same strat-
egy as Jakobsen in (Jakobsen, 1995), in order to de-
termine the elements of the current permutation to be
swapped. For a more detailed description of Jakob-
sen’s method in the case of simple substitution ciphers
we refer the reader to the original paper (Jakobsen,
1995). Figure 2 in (Jakobsen, 1995) shows that a ci-
phertext of length 600 built by a simple substitution
cipher can be entirely broken by this method. It is
clear that some modification of Jakobsen’s original al-
gorithm is necessary in order to make it applicable in
our setting as well. In particular, the definitions of the
matrices D and E must be changed. Their adopted
AutomatedCryptanalysisofBloomFilterEncryptionsofHealthRecords
9

definitions are introduced in subsection 4.3.
4.2 Atom Detection
As in (Niedermeyer et al., 2014), the basic principle
of our approach consists in the detection of atoms,
which represent the encryption of one single bigram
only. Since the Bloom filter of a string is created by
the superposition of at least a few atoms, the recon-
struction of the atoms given only a set of Bloom fil-
ters turns out to be difficult. Note that this task can-
not be solved in a satisfactory manner if Bloom filters
are considered isolatedly or in small groups because
in this case too many binary vectors will be wrongly
classified as atoms.
Let us give a short motivation for our novel
method aiming at atom detection. If the bitwise AND
operation is applied to a set of Bloom filters that have
one bigram β in common, at least all positions set to
one by β are equal to one in the result. However, for
prevalent bigrams it should be expected that all the
other positions are set to zero if a sufficient number of
Bloom filters are considered, i.e., the result would be
exactly the atom induced by the bigram β.
Of course, if an adversary has access to a set
of Bloom filters, s/he does not a priori know which
Bloom filters have a bigram in common. This obsta-
cle can be avoided as follows: Under the assumption
that the double hashing scheme is being used, the ad-
versary is able to determine for each combination of
bit positions from equation (1) the set of Bloom filters
for which all these positions are set to 1. Then, the
bitwise AND operation is applied to the set of these
Bloom filters. If the result coincides with the atom, it
is considered to be the realization of a bigram by the
adversary.
The resulting set of atoms was further reduced by
discarding atoms of Hamming weight
∑
999
i=0
b
i
equal
to 1, 2, 4 or 5 and keeping only atoms of Hamming
weight equal to 8, 10 or 20.
Otherwise, too many binary vectors would have
been classified incorrectly as atoms. The probability
that an atom has Hamming weight less than 8 in our
setting is equal to 0.008. This value can be derived in
analogy to Lemma A.1 and the subsequent example
in (Niedermeyer et al., 2014). We denote the num-
ber of atoms found by n. For our specific data set we
got n = 1,776. This result seems reasonable, because
the total number of possible atoms is bounded from
above by 2,187 and obviously not all of these atoms,
in particular atoms realized by rare bigrams, occur in
our simulated data. As we checked later on, 1,337
of the 1,776 extracted conjectured atoms were indeed
true atoms, that is to say atoms generated by one of
0
10000
20000
30000
name:A_
loc:EN
surname:ER
loc:N_
loc:ER
name:AN
surname:R_
name:E_
name:AR name:_M
Bigram
Count
Figure 4: Absolute frequencies of the 10 most frequent bi-
grams in our training data set.
the 2,187 bigrams. The subsequent analysis demon-
strates that this percentage of correct atom detection
is sufficient for a successful cryptanalysis. For each
atom α we determined the set of Bloom filters con-
taining this atom, i.e. Bloom filters for which all bit
positions of the atom are set to 1. We denote the atoms
with α
1
,. .. ,α
1776
according to decreasing frequency.
In order to give an illustrative example, we assert that
in the Bloom filter No. 850 the atoms α
5
, α
8
, α
14
,
α
15
, α
29
, α
33
, α
36
, α
46
, α
55
, α
106
, α
110
, α
123
, α
138
,
α
169
, α
194
, α
197
, α
218
, α
254
, α
309
, α
313
, α
317
, α
334
,
α
335
, α
396
, α
398
, α
453
, α
607
, α
668
, α
705
, α
782
, α
821
,
α
960
and α
1131
were detected.
In the subsequent section we explain how correla-
tions between the occurences of atoms in the Bloom
filters and bigrams in a training data set can be used
to give adequate definitions of the matrices D and E
that serve as the input of Jakobsen’s algorithm.
4.3 Correlation of Atoms and Bigrams
A naive assignment of bigrams to atoms is possible
only for few frequent bigrams. For example, if Ger-
man surnames, given names and birth locations are
considered together, the most frequent bigram is A
f
(the bigram A in the forename identifier) such that
the most frequent atom is likely to be the encryption
of this bigram. The absolute frequencies of the 10
most frequent bigrams in the considered training data
are illustrated in Figure 4.
Except for the first few bigrams, the bigram fre-
quencies are too close together such that naive match-
ing is not promising for automatic decipherment.
In the example of Bloom filter No. 850 already
introduced above, this naive assignment would lead to
the conjecture that the corresponding record contains
the following bigrams: N
l
, R
s
, CH
s
, N
f
, HE
l
,
l
,
SC
s
, S
f
, E
l
, L
f
, BE
s
, NI
f
, AR
s
, W
f
, P
f
, NG
s
, IR
f
,
HEALTHINF2015-InternationalConferenceonHealthInformatics
10

ET
s
, MI
s
, NI
s
, VE
l
, OS
l
, NS
s
, UN
s
, AT
s
, V
s
, LH
l
, OW
l
,
AA
s
, ZB
l
, RR
l
, DY
f
and MR
s
. However, from this list of
bigrams it is obviously impossible to reconstruct any
meaningful information.
For this reason, we also took correlations between
bigrams into account. For example, for records sam-
pled from the population of Germany the appearance
of the bigram CH
s
in a record makes the appearance
of the bigram SC
s
in the same record more likely be-
cause the trigram SCH frequently appears in German
surnames.
We model this kind of information on the corre-
lation of atoms and bigrams by means of two ma-
trices D and E. Assume that the attribution val-
ues of the records built from tokens of the alphabet
Σ = { ,A, B,. .. ,Z} are to be encrypted. Thus, for
each (string valued) identifier we have 729 possible
bigrams. Since the same bigram is encrypted differ-
ently for each identifier we have to distinguish be-
tween different instances of the same bigram. In our
setting we denote the bigram β for the surname, fore-
name and location identifier with β
s
, β
f
and β
l
, re-
spectively. Altogether, the set Σ
2
containing all possi-
ble bigrams consists of 3 · 729 = 2,187 elements.
Let us now introduce the matrix E containing in-
formation about the expected bigram correlations ob-
tained from the training data set. Note that the train-
ing data should be as similar to the encrypted data as
possible, e.g. a random sample from the same under-
lying population as the encrypted data. If the prevail-
ing Bloom filters are known to contain encryptions
of records from the German population, an attacker
would try to get access to a comparable database con-
taining the same identifiers. The attribute values of
this training data set are preprocessed analogously to
the preprocessing routine before the encryption pro-
cess. Then, the bigram sets for all the attribute values
are created. We denote the bigrams with β
1
,. .. ,β
2187
according to decreasing frequency. Let T be the to-
tal number of records in the training data set and t
i j
the number of records that contain both bigram β
i
and
bigram β
j
. Then the matrix E = (e
i j
)
i, j=1,...,2187
is
defined via
e
i j
=
(
t
i j
/T if i 6= j,
0 if i = j.
The matrix D is formed in a similar way on the ba-
sis of joint appearances of atoms in the Bloom filters.
Let N be the number of Bloom filters for which atoms
have been extracted. We denote the number of Bloom
filters that contain both atom α
i
and atom α
j
by b
i j
.
The matrix D = (d
i j
)
i, j=1,...,2187
is defined through
d
i j
=
(
b
i j
/N if i 6= j and i, j ≤ 1776,
0 if i = j or max(i, j) > 1776.
The procedure suggested by Jakobsen which was
described above can now directly be applied to the
matrices D and E:
OPTIMIZATION ALGORITHM.
Input: D,E as defined in section 4.3
Output: σ
opt
∈ S
2187
minimizing
f (σ) =
∑
i, j
|d
σ(i)σ( j)
− e
i
e
j
|
1: σ
opt
(i) = i ∀i  Initialization
2: min ← f (σ
opt
)
3: a,b ← 1
4: repeat
5: σ ← σ
opt
6: a ← a + 1
7: if a + b ≤ 2187 then
8: σ(a) ← σ
opt
(b), σ(b) ← σ
opt
(a)
9: else
10: a ← 1, b ← b + 1
11: if f (σ) < f (σ
opt
) then  Update
12: min ← f (σ)
13: σ
opt
← σ
14: a,b ← 1
15: until b = 2187
The progress of the optimization algorithm is il-
lustrated by means of Figure 5.
The result of the algorithm will be the final assign-
ment between atoms and bigrams defined by a permu-
tation σ
opt
∈ S
2187
and the assignment rule α
σ
opt
(i)
→
β
i
. This assignment is used to reconstruct the original
bigram sets encrypted in the Bloom filters.
For example, the bigrams ER
s
, R
s
, CH
s
, N
f
, HE
l
,
l
, SC
s
, S
f
, E
l
, HE
s
, K
l
, RL
l
, AR
l
, Z
s
, ON
f
, SI
f
, F
s
,
IS
s
, LS
l
, HW
l
, SO
f
, RU
l
, UR
s
, IM
f
, KA
l
, MO
f
, AV
f
, FI
s
,
UH
l
, HH
l
, SR
l
, UZ
l
and MR
s
were assigned to the Bloom
filter No. 850.
Figure 5: Progress of the optimization algorithm for our
data set. The initial value of the objective function is 370.99
and 2,812 updating steps were performed. The final value
of the objective function f (σ
opt
) was equal to 168.5.
AutomatedCryptanalysisofBloomFilterEncryptionsofHealthRecords
11

In the following section we describe how attribute
values were reassembled from the reconstructed bi-
gram sets.
4.4 Reconstruction of Attribute Values
In order to reconstruct the original attribute values of
the records, we separated the bigrams belonging to
different identifiers for each Bloom filter.
In the example of Bloom filter No. 850, we ob-
tained the bigrams N
f
, S
f
, ON
f
, SI
f
,SO
f
, IM
f
, MO
f
,
AV
f
for the forename identifier, the bigrams ER
s
, R
s
,
CH
s
, SC
s
, HE
s
, Z
s
, F
s
, IS
s
, UR
s
, FI
s
, MR
s
for the sur-
name identifier and finally the bigrams HE
l
,
l
, E
l
,
K
l
, RL
l
, AR
l
, LS
l
, HW
l
, RU
l
, KA
l
, UH
l
, HH
l
, SR
l
, UZ
l
for the location identifier. From this list it is already
possible to guess the original identifier values at first
glance.
Our fully automated approach to reconstructing
the original identifier values was to compare the ob-
tained bigram sets with a list of bigram sets gener-
ated from reference lists of surnames, names and lo-
cations. For Bloom filter No. 850, for example, an
adversary would correctly obtain that this Bloom fil-
ter encrypts a record belonging to the person Simon
Fischer from the German city Karlsruhe.
4.5 Results
By using the approach described above, we were able
to reconstruct 59.6% of the forenames, 73.9% of the
surnames and 99.7% of the locations correctly. For
44% of the 100,000 records all the identifier values
were recuperated successfully.
5 CONCLUSION
In this paper we demonstrate a successful fully au-
tomated attack on Bloom filters built from multiple
identifiers. We were able to recover approximately
77.7 % of the original identifier values. In contrast to
the assumptions in (Kuzu et al., 2012) and (Nieder-
meyer et al., 2014), that storing all identifiers in a sin-
gle Bloom filter makes it more difficult to attack, we
needed only moderate computational effort and pub-
licly available lists of forenames, surnames, and loca-
tions to reconstruct the identifiers. Note that there is
no huge impact of the size of the database containing
the Bloom filters. For our cryptanalysis it is sufficient
to perform the attack on a subset of the given Bloom
filters (100,000 as in our example should be adequate
in most cases). Then for the remaining Bloom fil-
ters it would be sufficient to check for the atoms con-
tained in those and to reconstruct the attribute values,
since most assignments of atoms to bigrams are al-
ready known. Thus, the time needed for cryptanalysis
is linear in the number of input Bloom filters. The
time needed for the detection of atoms is O(L
2
) since
there are L possible values for the hash functions f
and g in equation (1). Furthermore, the detection of
atoms could easily be parallelized to make the compu-
tation faster and values of L significantly larger than
L = 1,000 as considered in this paper would also have
negative effects on the time needed for performing the
linkage between two databases (note that in the large
scale study reported in (Randall et al., 2014) a Bloom
filter length of only 100 was considered). Thus, the
most time consuming step in our cryptanalysis should
be the optimization algorithm presented in subsection
4.3. Indeed, in the chosen parameter setup this proce-
dure took about 402 minutes on a notebook with 2.80
GHz Intel
R

Core running Ubuntu 14.04 LTS.
To sum up, we do not recommend the usage of
Bloom filters built from one or more identifiers, gen-
erated with the double hashing scheme, in appli-
cations where high security standards are required.
However, we applied our attack in a very special
scenario, because the generated databases were en-
crypted using the double hashing scheme. Thus, there
are options for an improvement of the setting.
For example Niedermeyer et al. (Niedermeyer
et al., 2014) proposed several methods such as fake
injections, salting or randomly selected hash values
to harden the Bloom filters. Hence, we are confident
that methods like those proposed by Niedermeyer et
al. show promise in the prevention of attacks like the
one presented in this paper.
ACKNOWLEDGEMENTS
Research of both authors was financially supported
by the research grant SCHN 586/19-1 of the Ger-
man Research Foundation (DFG) awarded to the head
of the Research Methodology Group, Rainer Schnell.
We thank him and the three anonymous reviewers for
their helpful comments.
REFERENCES
Bloom, B. H. (1970). Space/time trade-offs in hash coding
with allowable errors. Communications of the ACM,
13(7):422–426.
Herzog, T. N., Scheuren, F. J., and Winkler, W. E.
(2007). Data Quality and Record Linkage Techniques.
Springer, New York.
HEALTHINF2015-InternationalConferenceonHealthInformatics
12

Jakobsen, T. (1995). A fast method for the cryptanalysis of
substitution ciphers. Cryptologia, 19(3):265–274.
Jones, M., McEwan, P., Morgan, C. L., Peters, J. R., Good-
fellow, J., and Currie, C. J. (2005). Evaluation of the
pattern of treatment, level of anticoagulation control,
and outcome of treatment with warfarin in patients
with non-valvar atrial fibrillation: a record linkage
study in a large British population. Heart, 91(4):472–
477.
Kirsch, A. and Mitzenmacher, M. (2008). Less hashing,
same performance: Building a better Bloom filter.
Random Structures & Algorithms, 33(2):187–218.
Kuehni, C. E., Rueegg, C. S., Michel, G., Rebholz, C. E.,
Strippoli, M.-P. F., Niggli, F. K., Egger, M., and
von der Weid, N. X. (2012). Cohort profile: The Swiss
childhood cancer survivor study. International Jour-
nal of Epidemiology, 41(6):1553–1564.
Kuzu, M., Kantarcioglu, M., Durham, E., and Malin, B.
(2011). A constraint satisfaction cryptanalysis of
bloom filters in private record linkage. In Fischer-
H
¨
ubner, S. and Hopper, N., editors, Privacy Enhanc-
ing Technologies, volume 6794 of Lecture Notes in
Computer Science, pages 226–245. Springer, Berlin.
Kuzu, M., Kantarcioglu, M., Durham, E. A., Toth, C., and
Malin, B. (2012). A practical approach to achieve
private medical record linkage in light of public re-
sources. Journal of the American Medical Informatics
Association, 20(2):285–292.
Newman, T. B. and Brown, A. N. (1997). Use of commer-
cial record linkage software and vital statistics to iden-
tify patient deaths. Journal of the American Medical
Informatics Association, 4(3):233–237.
Niedermeyer, F., Steinmetzer, S., Kroll, M., and Schnell,
R. (2014). Cryptanalysis of basic Bloom filters used
for privacy preserving record linkage. Working Pa-
per NO.WP-GRLC-2014-04, German Record Link-
age Center, N
¨
urnberg.
Office for National Statistics (2013). Beyond 2011: Match-
ing anonymous data. Methods & Policies M9, ONS,
London.
Randall, S. M., Ferrante, A. M., Boyd, J. H., Bauer, J. K.,
and Semmens, J. B. (2014). Privacy-preserving record
linkage on large real world datasets. Journal of
Biomedical Informatics.
Randall, S. M., Ferrante, A. M., Boyd, J. H., and Semmens,
J. B. (2013). The effect of data cleaning on record
linkage quality. BMC Medical Informatics and Deci-
sion Making, 13(64).
Rocha, M. C. N. (2013). Vigil
ˆ
ancia dos
´
obitos Registrados
com Causa B
´
asica Hansen
´
ıase. Master thesis, Uni-
versidade de Bras
´
ılia, Bras
´
ılia.
Schnell, R., Bachteler, T., and Reiher, J. (2009). Privacy-
preserving record linkage using Bloom filters. BMC
Medical Informatics and Decision Making, 9(41):1–
11.
Schnell, R., Bachteler, T., and Reiher, J. (2011). A novel
error-tolerant anonymous linking code. Working Pa-
per NO.WP-GRLC-2011-02, German Record Link-
age Center, N
¨
urnberg.
Schnell, R., Richter, A., and Borgs, C. (2014). Performance
of different methods for privacy preserving record
linkage with large scale medical data sets. Presenta-
tion at International Health Data Linkage Conference,
Vancouver.
Van Den Brandt, P. A., Schouten, L. J., Goldbohm, R. A.,
Dorant, E., and Hunen, P. M. H. (1990). Develop-
ment of a record linkage protocol for use in the Dutch
cancer registry for epidemiological research. Interna-
tional Journal of Epidemiology, 19(3):553–558.
AutomatedCryptanalysisofBloomFilterEncryptionsofHealthRecords
13