
Approximate Analysis of Homeostasis of Gene Networks by Linear
Temporal Logic using Network Motifs
Sohei Ito
1
, Shigeki Hagihara
2
and Naoki Yonezaki
2
1
Department of Fisheries Distribution and Management, National Fisheries University,
2-7-1 Nagata-Honmachi, Shimonoseki, Yamaguchi, Japan
2
Department of Computer Science, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo, Japan
Keywords:
Gene Regulatory Network, Homeostasis, Temporal Logic, Strong Satisfiability, Network Motif, Systems
Biology.
Abstract:
We proposed a novel framework to analyse homeostasis of gene networks using linear temporal logic. We
formulate a kind of homeostasis as strong satisfiability of reactive system specifications. Both behaviours and
properties of gene networks are specified in linear temporal logic and homeostasis of the network is checked
by strong satisfiability checkers. Though this framework is simple and applicable for many networks, the
computational complexity is heavy and large networks cannot be directly analysed. In this paper we present an
approximate analysis method to mitigate this computational difficulty. We approximately specify a network
specification using fewer propositions such that approximated specifications guarantee homeostasis of the
network. However it is difficult to find such safely approximated specifications for any gene network. Thus
we present approximate specifications for network motifs, which are common patterns appearing in many gene
networks. We demonstrate our approximate method and see that our approximate method is quite efficient in
analysing large networks.
1 INTRODUCTION
Although homeostasis in biological systems is a re-
markable feature of life, it has been considered to be
elusive and difficult to be analysed. Ito et al. (Ito
et al., 2014) proposed a mathematical and precise def-
inition of homeostasis in gene networks and provided
a method for analysing it. Their approach is based
on Ito et al.’s constraint-based modelling of gene net-
works (Ito et al., 2010; Ito et al., 2013b; Ito et al.,
2013a) using linear temporal logic (LTL) (Emerson,
1990). In their method, possible behaviours of gene
networks are characterised as LTL formulae, which
means that possible behaviours are behaviours that
satisfy the constraints (called network specifications)
given as LTL-formulae. With network specifications
and given biological property, the homeostasis of net-
work is analysed by checking whether the formulae
is realisable or not. The specification which sat-
isfies realisability (homeostasis) can respond to any
input sequence (any stimulus) without violating the
specification (breaking its internal functions). This
framework for analysing gene networks belongs to
the same lineage as the verification of reactive system
specifications (Pnueli and Rosner, 1989; Abadi et al.,
1989). The problem, however, is the computational
complexity of realisability problem of LTL which is
2EXPTIME-complete in the size of a formula (Pnueli
and Rosner, 1989). Since the size of a formula is pro-
portional to the size of a network, direct analysis of a
large network is intractable in general.
In this paper, we propose the notion of weak
homeostasis which is close to Ito et al.’s definition but
a bit weaker. We formulate this notion by strong sat-
isfiability (Mori and Yonezaki, 1993) which is weaker
than realisability. Strong satisfiability is proposed
to approximate realisability and has a more efficient
checking algorithm than realisability has. However,
the complexity of checking strong satisfiability is
still high (EXPSPACE-complete (Shimakawa et al.,
2013)) and we need to devise some efficient method
to mitigate this difficulty. Fortunately, we found that
we can import the approximate analysis method for
checking satisfiability (Ito et al., 2013b) to strong sat-
isfiability checking, which is the main contribution of
this paper. The key idea of approximate analysis is to
simplify a network specification using fewer propo-
sitions and approximate the possible behaviours of a
93
Ito S., Hagihara S. and Yonezaki N..
Approximate Analysis of Homeostasis of Gene Networks by Linear Temporal Logic using Network Motifs.
DOI: 10.5220/0005177000930101
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2015), pages 93-101
ISBN: 978-989-758-070-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

network. We prove that the certain class of approxi-
mate specifications can be used instead of the original
specifications to check weak homeostasis of gene net-
works. The problem is that it is difficult to find such
safe approximate specifications for arbitrary gene net-
works. Thus we use Ito et al.’s approximate specifica-
tions (Ito et al., 2013b) for network motifs, which are
common patterns in gene networks (Alon, 2007). We
demonstrate our approximate method for several net-
works from real biological systems. This experiment
shows that the cost of analysis is drastically reduced
by our approximate analysis.
This paper is organised as follows. In section 2
we introduce LTL and show how we model possible
behaviours of gene networks. In section 3 we define
the notion of weak homeostasis using strong satisfia-
bility of LTL. In section 4 we introduce the approx-
imate method for analysing weak homeostasis. We
also present approximate specifications for network
motifs. In section 5 we show experimental results of
our approximate method and see how we benefit from
it. The final section offers conclusion and future di-
rections.
2 PRELIMINARY
In this section we introduce linear temporal logic
(LTL) upon which our constraint-based modelling
method is based. Then we review how we charac-
terise possible behaviours of a given network using
LTL (Ito et al., 2010; Ito et al., 2013b; Ito et al.,
2013a).
2.1 Linear Temporal Logic
Let A be a finite set. We write A
ω
for the set of all
infinite sequences on A. We write σ[i] for the i-th el-
ement of σ ∈ A
ω
. Let AP be a set of propositions. A
time structure is a sequence σ ∈ (2
AP
)
ω
where 2
AP
is
the powerset of AP. The formulae in LTL are defined
as follows.
• p ∈ AP is a formula.
• If φ and ψ are formulae, then ¬φ,φ∧ψ,φ ∨ ψ and
φUψ are also formulae.
Let σ be a time structure and φ be a formula. We
write σ |= φ to mean that φ is true in σ, and we say
σ satisfies φ. The satisfaction relation |= is defined as
follows.
Figure 1: A gene network in which x, y and z are genes.
Plus-edges represent activation relationship.
σ |= p iff p ∈ σ[0] for p ∈ AP
σ |= ¬φ iff σ 6|= φ
σ |= φ ∧ ψ iff σ |= φ and σ |= ψ
σ |= φ ∨ ψ iff σ |= φ or σ |= ψ
σ |= φUψ iff (∃i ≥ 0)(σ
i
|= ψ
and ∀ j(0 ≤ j < i)σ
j
|= φ)
where σ
i
= σ[i]σ[i+ 1] . . ., i.e. the i-th suffix of σ. We
say σ a model of φ when σ |= φ.
In the rest of the paper we use the following ab-
breviations: ⊥ ≡ p ∧ ¬p for some p ∈ AP, ⊤ ≡ ¬⊥,
φ → ψ ≡ ¬φ ∨ ψ, φ ↔ ψ ≡ (φ → ψ) ∧ (ψ → φ),
Fφ ≡ ⊤Uφ, Gφ ≡ ¬F¬φ, and φWψ ≡ (φUψ) ∨ Gφ.
We assume that ∧, ∨ and U bind more strongly than
→ and unary connectives bind more strongly than bi-
nary ones.
2.2 Conceptualising Behaviours of a
Gene Network as Time Structure
The basic idea of modelling possible behaviours of
a gene network is that we abstract time series of dy-
namic behaviours of gene networks as time structures.
For example, given a network depicted in Fig. 1 in
which gene x activates gene y and gene y activates
gene z, we consider an example dynamic behaviour
of this network depicted in Fig. 2. The expression
levels x
y
and y
z
in Fig. 2 are the threshold of gene x
to activate gene y and that of gene y to activate gene z,
respectively. If a gene is expressed beyond a thresh-
old to activate (or inhibit) a gene, its regulation effects
start to work. For example, when gene x is expressed
beyond the threshold x
y
(e.g. duration between time
t
1
and t
3
), gene y is ON and begins to be expressed.
If we verbally describe the network behaviour, we
only need to mention that whether a gene is ON or
OFF, whether a gene is expressed beyond its thresh-
olds
1
and how such situation changes over time. Such
atomic facts to describe a situation of a network can
be represented by propositions. In the case of net-
work depicted in Fig. 1, we introduce the following
propositions to describe the behaviour:
• on
x
,on
y
,on
z
: whether gene x, y and z are ON, re-
spectively.
• x
y
,y
z
: whether gene x is expressed beyond the
1
In general, there should be multiple thresholds for each
gene.
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
94

x
y
z
t
base
base
base
t
0
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
8
t
9
x
y
y
z
t
t
Figure 2: Example behaviour of the network depicted in
Fig. 1. The level x
y
is the threshold of gene x for activating
gene y and y
z
is the threshold of gene y for activating gene
z.
0 1 2 3 4 5 6 7 8 9 10
Figure 3: Representation of behaviour depicted in Fig. 2 as
a time structure.
threshold x
y
, and whether gene y is expressed be-
yond the threshold y
z
, respectively
2
.
Using these propositions as the set AP of atomic
propositions, we have a time structure σ ∈ (2
AP
)
ω
de-
picted in Fig. 3. Note that state 0 corresponds to the
interval [0,t
0
), state 1 to [t
0
,t
1
), and so on.
2.3 Modelling Possible Behaviours of a
Network in LTL
Based on the abstraction of behaviours of a net-
work as a time structure, we characterise possible be-
haviours of a gene network as the set of the models of
a suitable LTL formula, which is obtained by a given
network. Formally, for a given network G, we specify
an LTL formula ϕ
G
which is intended to characterise
the set of possible behaviours of G. Then the set of
possible behaviours is the set {σ ∈ (2
AP
)
ω
| σ |= ϕ
G
}
(i.e. σ is a model of ϕ
G
).
The problem is how we obtain a such formula.
2
Although the same symbols (i.e. x
y
and y
x
) are used to
represent both thresholds and propositions, we can clearly
distinguish them from the context.
This is solved by the following principles about be-
haviours of gene networks.
• A gene is ON when its activators are expressed
beyond some thresholds.
• A gene is OFF when its inhibitors are expressed
beyond some thresholds.
• If a gene is ON, its expression level increases.
• If a gene is OFF, its expression level decreases.
Fortunately, these principles can be naturally de-
scribed in LTL. In the following we show how we de-
scribe the above principles.
Conditions for Activation and Inhibition of Genes.
In simple situation such that gene x alone activates
gene y, gene y is ON if gene x is expressed beyond
the threshold x
y
. This is described as
G(x
y
→ on
y
).
Another choice is G(x
y
↔ on
y
) which says that gene
y is ON if, and only if gene x is expressed beyond
the threshold x
y
. If we consider no other (implicit)
regulator for gene y, the latter specification may be
reasonable. Similarly, if gene x alone inhibits gene
y, gene y is OFF if gene x is expressed beyond the
threshold x
y
. This is described as
G(x
y
→ ¬on
y
).
As in the case of activation , we may write G(x
y
↔
¬on
y
).
For more complicated situation, a gene has mul-
tiple regulators and the effect may be different from
one another. For example, consider that gene u is ac-
tivated by both gene x and y, and inhibited by gene z.
Generally we do not know the regulation function of
u which has three inputs. In such situation, we only
describe sufficientconditionsfor u’s activation and in-
hibition: gene u is ON if gene x is expressed beyond
x
u
, gene y beyond y
u
and gene z below z
u
. This is
described as
G(x
u
∧ y
u
∧ ¬z
u
→ on
u
).
Moreover, gene u is OFF if gene x is expressed below
x
u
and gene y below y
u
and gene z beyond z
u
. This is
described as
G(¬x
u
∧ ¬y
u
∧ z
u
→ ¬on
u
).
If we (may partially) know about the regulation
function, we can reflect such knowledge in the speci-
fication. For example the positive effect of gene x and
y are merged by ‘OR’, we can describe as
G((x
u
∨ y
u
) ∧¬z
u
→ on
u
),
G((¬x
u
∧ ¬y
u
) ∧z
u
→ ¬on
u
).
ApproximateAnalysisofHomeostasisofGeneNetworksbyLinearTemporalLogicusingNetworkMotifs
95

Total Order of Thresholds. Since a gene may have
multiple thresholds, we need to specify a total order of
them. Assume that gene x has thresholds x
1
,x
2
,. . . ,x
m
in this order. This order relation can be described in
LTL as follows:
^
1≤i<m−1
G(x
i+1
→ x
i
).
For example, G(x
2
→ x
1
) means that if the cur-
rent expression level is beyond the threshold x
2
, it is
also beyond x
1
since x
1
is lower than x
2
. Note that
the proposition x
i
is interpreted as gene x is expressed
beyond the threshold x
i
.
Change of Expression Levels When Genes Are
ON. Assume that gene x has its thresholds
x
1
,x
2
,. . . , x
m
in this order. If gene x is ON, the ex-
pression level of x increases over time. For example,
if the current level of gene x is between x
i
and x
i+1
and x is ON, x will cross the threshold x
i+1
in future
(if gene x does not become OFF prematurely). This
fact is simply described as follows:
G(on
x
∧ x
i
→ (x
i
U(x
i+1
∨ ¬on
x
)))
where i ∈ {1, . .. , m− 1}. This formula says that gene
x must cross the threshold x
i+1
unless gene x becomes
OFF. That is, we do not allow that the expression level
of gene x can be equilibrated between the level x
i
and
x
i+1
if gene x is indefinitely ON. This specification is
called strong specification. To allow such equilibrated
behaviour, we specify as:
G(on
x
∧ x
i
→ (x
i
W¬on
x
))
where i ∈ {1,. . . ,m− 1}. This kind of specification is
called weak specification. The choice of strong speci-
fication and weak specification depends on a situation
or an assumption of the analysis which we are to per-
form.
We need special treatment for the level below x
1
(the lowest threshold) and the level above x
m
(the
highest threshold). In the case that the expression
level of x is below x
1
, none of the propositions among
x
1
,. . . , x
m
are true. If gene x is ON, it will cross x
1
in future (unless gene x becomes OFF prematurely).
This can be described as:
G(on
x
→ F(x
1
∨ ¬on
x
)).
If gene x is expressed above x
m
, since we do not have
the threshold over it, its expression level does not in-
crease further. Instead, gene x will keep its level (un-
less gene x becomes OFF). This can be described as:
G(on
x
∧ x
m
→ (x
m
W¬on
x
)).
Change of Expression Level When Genes Are
OFF. We also assume that gene x has its thresholds
x
1
,x
2
,. . . , x
m
in this order. The specification for the
case where genes are OFF is symmetric to the case
where genes are ON. Thus we only show formulae.
G(¬on
x
∧ ¬x
i
→ (¬x
i
U(¬x
i−1
∨ on
x
))), (strong)
G(¬on
x
∧ ¬x
i
→ (¬x
i
Won
x
)), (weak)
G(¬on
x
→ F(¬x
m
∨ on
x
)),
G(¬on
x
∧ ¬x
1
→ (¬x
1
W¬on
x
)).
3 WEAK HOMEOSTASIS AS
STRONG SATISFIABILITY
In this section we show how we formulate weak
homeostasis of a gene network by the notion of strong
satisfiability of reactive system specifications (Mori
and Yonezaki, 1993).
A reactive system is a system which reacts to ex-
ternal events from an environment and produces out-
put events or controls its internal states in appropriate
timing. How it reacts is dictated by specifications.
LTL is known to be suitable to write reactive sys-
tem specifications formally (Pnueli and Rosner, 1989;
Abadi et al., 1989). Formally, a reactive system speci-
fication is represented as the triple hE,I,ϕi where E is
a set of external propositions (corresponding to exter-
nal events), I is a set of internal propositions (corre-
sponding to internal or output events) and ϕ is an LTL
formula consists of atomic propositions from E ∪ I.
Then the notion of strong satisfiability of a reactive
system specification is defined as follows.
Definition 1 (Strong Satisfiability). LTL specification
hE,I,ϕi is strongly satisfiable if
∀ ˜x ∈ (2
E
)
ω
∃ ˜y ∈ (2
I
)
ω
.h ˜x, ˜yi |= ϕ.
Here ˜x = x
0
x
1
.. . (each x
i
⊆ E), ˜y = y
0
y
1
.. . (each
y
i
⊆ I) and h˜x, ˜yi = (x
0
∪ y
0
)(x
1
∪ y
1
). . . .
Intuitively a specification hE, I,ϕi is strongly sat-
isfiable if for any infinite sequence of external propo-
sitions there exists an infinite sequence of internal
propositions such that its behaviour satisfies the spec-
ification ϕ.
Now we consider the relationship of this notion to
homeostasis of gene networks. Homeostasis is infor-
mally stated as the tendency of a system to maintain
its internal condition desirable against any situation
or stimulus. In other words, the problem of analysing
homeostasis of a gene network is to check whether a
network satisfies a given property against any exter-
nal input sequence. The purpose of this section is to
present a formal definition for this problem.
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
96

A gene network can be regarded as reactive sys-
tems, since it reacts to external inputs (e.g. from
environment or other cells) and determines its inter-
nal states. In section 2.3, we show how we spec-
ify possible behaviours of a given network in LTL.
Then we can regard a behaviour specification of a
network (say ϕ) as a reactive system specification, if
we determine which propositions correspond to in-
puts or outputs. For example, let us consider the
example network depicted in Fig. 1 again. In that
network we do not have external inputs. Thus we
assume gene x accepts positive inputs from environ-
ment. Then we introduce two propositions in
x
and
e
x
. The proposition in
x
represents whether input is
coming and e
x
represents whether the level of the in-
put is beyond the threshold above which gene x is
activated. Then we have the following propositions:
{in
x
,on
x
,on
y
,on
z
,e
x
,x
y
,y
z
}. The division of external
propositions E and internal propositions I is as fol-
lows: E = { in
x
}, I = {on
x
,on
y
,on
z
,e
x
,x
y
,y
z
}. Note
that the environment only controls in
x
which means
the environment is only able to determine whether it
gives the input to gene x or not. Whether the level
of input exceeds the level e
x
is determined by the be-
haviour specification. Thus e
x
is internal propositions.
The specification for change of levels of inputs is the
same as the case of gene expressions:
G(in
x
→ F(e
x
∨ ¬in
x
))
G(in
x
∧ e
x
→ (e
x
W¬in
x
))
G(¬in
x
→ F(¬e
x
∨ in
x
))
G(¬in
x
∧ ¬e
x
→ (¬e
x
Win
x
))
Now we introduce a network property ψ (specified
in LTL) of a given network which represents a desir-
able function of the network. We are to check whether
the property holds against any input sequences. We
can give any property like stability (e.g. a certain gene
is always ON) or oscillation (e.g. when a gene is ON,
it will later be OFF) in LTL.
The problem of checking whether a network
whose behaviours are specified by ϕ satisfies ψ for
any input sequence is formally stated as follows.
Definition 2. Let E be the set of external proposi-
tions, I be the set of internal propositions and E and
I are disjoint. Let AP = E ∪ I be the set of atomic
propositions. A property ψ is weakly homeostatic
with respect to a behaviour specification of a network
hE, I, ϕi if hE, I, ϕ∧ψi is strongly satisfiable. Here ϕ
and ψ are written in LTL with AP.
Note that Ito et al.’s definition of homeostasis is
that hE, I, ϕ ∧ ψi is realisable (Ito et al., 2014). The
reason why this definition is weak homeostasis is that
the network is not required to determine its inter-
nal states at some time-point only from the input se-
quences which is available at that time (i.e. finite in-
put sequences), which is the requirement for realis-
able specifications. In other words, the network can
use infinite input sequences to determine its internal
states at any time. Thus the homeostasis we capture
in this definition is weak compared to that of Ito et
al.’s definition based on realisability. Although the
homeostasis we capture in this work is weak, we still
have an biological insight for a homeostasis of gene
networks. Since strong satisfiability is necessary con-
dition of realisability, if a specification is proved to be
not strongly satisfiable (i.e. weakly homeostatic), we
see that it is not realisable (i.e. homeostatic).
This definition reduces the problem of checking
weak homeostasis to the problem of checking strong
satisfiability of reactive system specifications. Unfor-
tunately, the complexity of strong satisfiability check-
ing of LTL formula is EXPSPACE-complete in the
size of formulae (Shimakawa et al., 2013), which is
still high. In our framework, the size of a formula
obtained from a gene network is proportional to the
size of the network. Due to the high-complexity of
strong satisfiability checking, direct analyses of large
networks are generally intractable. In the next sec-
tion we introduce an approximate method to ease the
analysis of large networks.
4 APPROXIMATE ANALYSIS
The factor which is critical to the performance of
strong satisfiability checking is the size of a formula.
Thus reducing the size of a formula is a natural solu-
tion to overcome this computational difficulty. How-
ever, it is unclear that we can safely reduce the size of
a formula.
Ito et al. (Ito et al., 2013b) proved that such safe
reduction of the size of a formula is feasible. They
approximate the set of possible behaviours of a given
network using fewer propositions. Their approximate
method guarantees that if an approximate specifica-
tion is satisfiable, the original specification is also sat-
isfiable. Here we say a formula ϕ is satisfiable if there
exists a behaviour σ such that σ |= ϕ. Since satisfiabil-
ity is a weaker property than strong satisfiability, it is
unclear that their method is also feasible in analysing
weak homeostasis of a gene network.
This section extends their result to analyse weak
homeostasis of a gene network. Intuitively, the idea
of the approximate method is to shrink the set of pos-
sible behaviours by approximate specifications. This
means that the network has fewer choices to react to
the environmental inputs. If we can prove that the
ApproximateAnalysisofHomeostasisofGeneNetworksbyLinearTemporalLogicusingNetworkMotifs
97

network can still respond to any environmental in-
puts in such restricted choices compared to original
behaviour sets, it guarantees that the network surely
reacts to any inputs. For formal development of our
approximate analysis, we first introduce some notions
and related theorems.
Definition 3. Let ϕ be an LTL formula. Prop(ϕ) de-
notes the set of propositions occurring in ϕ. More-
over, if Prop(ϕ) is partitioned into external propo-
sitions and internal propositions, EP(ϕ) denotes the
set of external propositions occurring in ϕ and IP(ϕ)
denotes the set of internal propositions occurring in
ϕ. Clearly EP(ϕ) ∩ IP(ϕ) =
/
0 and EP(ϕ) ∪ IP(ϕ) =
Prop(ϕ).
The next definition is of the B¨uchi automaton,
which is a kind of ω-automata accepting infinite
words.
Definition 4. A B¨uchi automaton is a quintuple hQ,
Σ, δ, q
I
, Fi, where Q is a finite set of states, Σ is a fi-
nite alphabet, δ : Q× Σ → P(Q) is the state transition
function, q
I
∈ Q is the initial state, and F ⊆ Q is the
set of accepting states. A run of a B
¨
uchi automaton on
an infinite word α = α[0]α[1]· ·· ∈ Σ
ω
is an infinite se-
quence ρ = ρ[0]ρ[1]·· · ∈ Q
ω
, such that ρ[0] = q
I
and
ρ[i+ 1] ∈ δ(ρ[i], α[i]) for all i ≥ 0. An infinite word α
is accepted by the automaton if the run over α visits
at least one state in F infinitely often. We denote the
set of infinite words accepted by an automaton A by
L(A).
The next theorem (Vardi and Wolper, 1994) states
that we can construct a B¨uchi automaton that exactly
accepts the models of LTL formula ϕ.
Theorem 1. Given an LTL formula ϕ, one can con-
struct a B
¨
uchi automaton A
ϕ
= hQ, Σ,δ, q
I
,Fi such
that |Q| is in 2
O(|ϕ|)
, Σ = 2
Prop(ϕ)
and L(A
ϕ
) = {σ ∈
(2
Prop(ϕ)
)
ω
| σ |= ϕ}.
The above theorem says that the set of time struc-
tures which satisfies formula ϕ is obtained by L(A
ϕ
).
Definition 5. Let A ⊆ B and σ ∈ (2
B
)
ω
. We denote
σ|
A
for the pointwise restriction of σ on A, i.e. σ|
A
=
(σ[0]|
A
)(σ[1]|
A
). . . . Assume L ⊆ (2
B
)
ω
. We denote
L|
A
for the element-wise restriction of set L on A, i.e.
L|
A
= {σ|
A
| σ ∈ L}.
Then we introduce an approximate relation be-
tween LTL formulae.
Definition 6. Let ϕ and ϕ
′
be LTL formulae such that
EP(ϕ) = EP(ϕ
′
) and IP(ϕ
′
) ⊆ IP(ϕ). We define the
relation ⊑ as follows:
ϕ
′
⊑ ϕ
def
⇐⇒ L(A
ϕ
′
) ⊆ L(A
ϕ
)|
Prop(ϕ
′
)
Note that Prop(ϕ
′
) ⊆ Prop(ϕ).
We say that ϕ
′
is a lower approximation of ϕ if
ϕ
′
⊑ ϕ. The formula ϕ
′
has fewer propositions than ϕ.
Our approximatemethod is to check strong satisfiabil-
ity of the specification hEP(ϕ
′
),IP(ϕ
′
),ϕ
′
i instead of
hEP(ϕ),IP(ϕ),ϕi in checking strong satisfiability. To
guaranteethe correctness of this approximate method,
we need to prove that if the approximate specifica-
tion hEP(ϕ
′
),IP(ϕ
′
),ϕ
′
i is strongly satisfiable, so is
hEP(ϕ),IP(ϕ),ϕi. The rest of this section is devoted
to prove this correctness.
First we prove the following lemma.
Lemma 1. Assume ϕ
′
⊑ ϕ. For any σ
′
∈ (2
Prop(ϕ
′
)
)
ω
,
if σ
′
|= ϕ
′
then there exists σ ∈ (2
Prop(ϕ)
)
ω
such that
σ |= ϕ and σ|
Prop(ϕ
′
)
= σ
′
.
Proof. By definition of ϕ
′
⊑ ϕ, we have Prop(ϕ
′
) ⊆
Prop(ϕ) and L(A
ϕ
′
) ⊆ L(A
ϕ
)|
Prop(ϕ
′
)
. Suppose σ
′
|=
ϕ
′
for σ
′
∈ (2
Prop(ϕ
′
)
)
ω
, we have σ
′
∈ L(A
ϕ
′
) by the-
orem 1. By assumption we have σ
′
∈ L(A
ϕ
)|
Prop(ϕ
′
)
.
By definition 5, there exists σ ∈ (2
Prop(ϕ)
)
ω
such that
σ ∈ L(A
ϕ
) and σ|
Prop(ϕ)
= σ
′
.
From this theorem we immediately have the fol-
lowing:
Corollary 1. If ϕ
′
⊑ ϕ, there is a mapping ℓ
ϕ
′
,ϕ
:
(2
Prop(ϕ
′
)
)
ω
→ (2
Prop(ϕ)
)
ω
such that if σ
′
|= ϕ
′
then
ℓ
ϕ
′
,ϕ
(σ
′
) |= ϕ.
Now we prove our main theorem.
Theorem2. Supposeϕ
′
⊑ ϕ. If hEP(ϕ
′
),IP(ϕ
′
),ϕ
′
i is
strongly satisfiable then hEP(ϕ),IP(ϕ),ϕi is strongly
satisfiable.
Proof. Since ϕ
′
is strongly satisfiable, for any
˜x ∈ (2
EP(ϕ
′
)
)
ω
there exists ˜y ∈ (2
IP(ϕ
′
)
)
ω
such that
h ˜x, ˜yi |= ϕ
′
. By definition of ϕ
′
⊑ ϕ, we have h ˜x, ˜yi ∈
L(A
ϕ
)|
Prop(ϕ
′
)
. From corollary 1, there exists a func-
tion ℓ
ϕ
′
,ϕ
such that ℓ
ϕ
′
,ϕ
(h ˜x, ˜yi) |= ϕ. Since EP(ϕ
′
) =
EP(ϕ), we have h ˜x, ˜zi = ℓ
ϕ
′
,ϕ
(h ˜x, ˜yi) for some ˜z ∈
(2
IP(ϕ)
)
ω
.
To prove the correctness of approximate analysis
of weak homeostasis, we need to prove the following
corollary (proof is omitted).
Corollary 2. Suppose ϕ
′
⊑ ϕ and Prop(ψ) ⊆
Prop(ϕ
′
). If hEP(ϕ
′
∧ ψ),IP(ϕ
′
∧ ψ), ϕ
′
∧ ψi is
strongly satisfiable then hEP(ϕ∧ψ), IP(ϕ∧ψ),ϕ∧ψi
is strongly satisfiable.
Thanks to corollary 2, in analysing weak home-
ostasis of a network whose behaviour specification is
ϕ, we can simplify the specification ϕ to ϕ
′
such that
ϕ
′
⊑ ϕ. The problem is that it is unclear whether we
can systematically obtain such approximate specifi-
cation ϕ
′
for any LTL formula ϕ. Ito et al., how-
ever, showed that for a specific class of networks,
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
98

malT
crp
malI
-
-
-
-
u x
vv
zz z
y
input
input
subnetwork1
subnetwork2
+
-
Figure 4: A network in E. coli.
called network motifs, we have approximate specifica-
tions (Ito et al., 2013b). Network motifs are common
network patterns recurring in many gene networks
(Alon, 2007). Thus approximate specifications for
network motifs are useful when we analyse real gene
networks. We use Ito et al.’s approximate specifica-
tions for five network motifs (Ito et al., 2013b), neg-
ative auto-regulation, coherent type 1 feed-forward
loop, incoherent type 1 feed-forward loop, single-
input module and multi-output feed-forwardloop. We
cannot find space for showing them. Interested reader
may wish to consult it.
5 EXPERIMENTAL RESULTS
In this section we show experimental results of our
approximate method in analysing weak homeostasis
of gene networks. For the experiment we use a net-
work in Escherichiacoli (Alon, 2007) depicted in Fig.
4 and a network in Arabidopsis thaliana which is ob-
tained from ReIN
3
and is depicted in Fig. 5. In the
network of Fig. 4, we have one single-input module
(consisting of gene u, v
1
and v
2
), two negative auto-
regulations (gene crp and malI), and one multi-output
feed-forward loop (consisting of gene x, y, z
1
, z
2
and
z
3
). In Fig. 5, we have one negative auto-regulation
(gene AP2) and one single-input module whose mas-
ter gene is GL1/GL3 and target genes are those reg-
ulated by the master gene. Some target genes have
another regulator but such case can be easily taken
into consideration in the approximate specification.
We show the part of the behaviour specification of
the network of Fig. 4.
3
http://arabidopsis.med.ohio-state.edu/REIN/
ARP7
FDH
At3g50790
RBR1
SIM
ATMYBL2
ETC1
GL2
At5g28350
MYC
At3g50800
TRY
CAPRICE
AtGRAS30
At4g20960
KIS
TTG2
CPL3
GL1/
GL3
AP2
-
-
AtPLDf1
-
HY5
input
-
Figure 5: A network in Arabidopsis.
G(u
v
1
↔ on
v
1
)∧
G(u
v
2
↔ on
v
2
)∧
G(on
u
→ F(u
v
1
∨ ¬on
u
))∧
G((on
u
∧ u
v
1
) → (u
v
1
U(¬on
u
∨ u
v
2
)))∧
G((on
u
∧ u
v
2
) → (u
v
2
W¬on
u
)) ∧ .. .
This specification can be approximated as:
G(on
u
→ F(on
v
1
∨ ¬on
u
))∧
G((on
u
∧ on
v
1
) → (on
v
1
W¬on
u
))∧
G((on
u
∧ on
v
2
) → (on
v
2
W¬on
u
)) ∧ .. .
As we can see, we no longer use propositions u
v
1
and
u
v
2
.
In this experiment we use three variations of spec-
ifications for each network – specification for the en-
tire network and its two subnetworks. Subnetworks
are obtained by eliminating some genes and edges
from the entire network as shown in Fig. 4 and 5.
We assume that the network depicted in Fig. 4 re-
ceives two inputs and the network depicted in Fig. 5
receives one input, as depicted. The property we con-
sider in this experiment is that if a certain gene is ac-
tivated, it will be suppressed afterward. We consider
the same type of property for both of the networks.
This property is described as:
G(on → F¬on)
where on proposition is for gene z
1
in the network
Fig. 4 and for gene TTG2 in the network Fig. 5. This
amounts to check whether the networks of Fig. 4 (Fig.
5) can suppress gene z
1
(TTG2) against any environ-
mental input sequence. In the network of Fig. 4, gene
z
1
is activated by gene x and gene x receives the nega-
tive input. Thus when the negative input never comes,
ApproximateAnalysisofHomeostasisofGeneNetworksbyLinearTemporalLogicusingNetworkMotifs
99
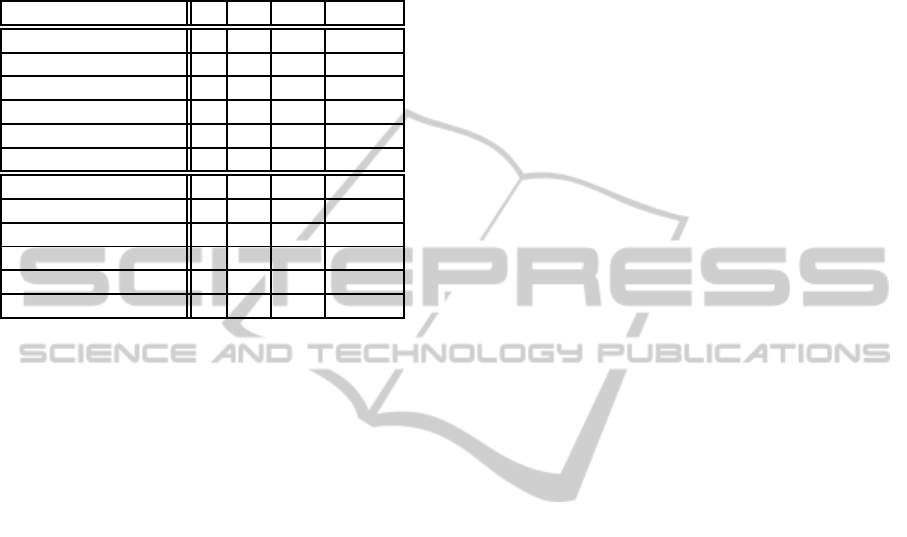
Table 1: Experimental results for checking weak homeosta-
sis of networks (i.e. we have no assumptions of environ-
mental inputs). Columns ’E’ and ’I’ respectively show the
numbers of external propositions and internal propositions.
Column ’S’ shows the size of a formula. Column ’T’ shows
the time of analysis (in seconds). The lower half of the table
shows the result of approximate analysis.
Network E I S T
Fig. 4 2 30 679 >3600
Fig. 4 (sub1) 2 24 572 >3600
Fig. 4 (sub2) 2 19 459 408.87
Fig. 5 1 46 869 >3600
Fig. 5 (sub1) 1 23 449 >3600
Fig. 5 (sub2) 1 13 269 0.10
Fig. 4 (appr.) 2 18 448 176.80
Fig. 4 (appr.) (sub1) 2 14 354 8.35
Fig. 4 (appr.) (sub2) 2 10 278 0.752
Fig. 5 (appr.) 1 30 692 11.07
Fig. 5 (appr.) (sub1) 1 16 379 0.17
Fig. 5 (appr.) (sub2) 1 9 231 0.04
gene x is easy to be ON and afterward gene z
1
will
be ON. However, malT is the gene necessary to acti-
vate gene x, and its expression can be controlled by
the network. Thus the network can control malT to
be OFF so that gene x cannot be ON. Therefore the
property is homeostatic. Similar informal reasoning
shows that the property for the network of Fig. 5 is
also homeostatic.
We show the results of each analysis in table 1.
These experiments are performed on a computer with
Intel Core i7-3820 3.60GHz CPU and 32GB mem-
ory. We used Shimakawa et al.’s strong satisfiability
checker (Shimakawa et al., 2014) for this experiment.
In example analyses reported in table 1, non-
approximated analyses were successful only for the
smallest network specifications (subnetwork2 for
both networks). In approximated analyses, however,
all specifications were successful. By comparing the
results of the network specification Fig.4 (sub2) and
its approximated version, we see that approximated
method improves the analysis speed by 540 times.
These results show that our approximate method is
effective.
6 CONCLUSIONS
In this paper we presented an approximate method for
analysing homeostasis of gene networks using net-
work motifs. We are investigating that whether our
approximate analysis method can be used to check
not only strong satisfiability but also realisability of
LTL to enable approximate analysis of homeostasis
based on the formulation by realisability (Ito et al.,
2014). For further improvement, we are interested in
whether Ito et al.’s modular method (Ito et al., 2013a)
is available in analysing (weak) homeostasis of gene
networks. Since modular analysis can be used in com-
bination with the approximate analysis, we further ex-
tend the limits of tractable networks. Using these re-
sults, we now should try to solve real problems in bi-
ology.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
Number 26730153. We also appreciate the help of
Dr. Masaya Shimakawa and Dr. Takashi Tomita for
checking proofs and giving invaluable comments.
REFERENCES
Abadi, M., Lamport, L., and Wolper, P. (1989). Realiz-
able and unrealizable specifications of reactive sys-
tems. In ICALP ’89: Proceedings of the 16th Interna-
tional Colloquium on Automata, Languages and Pro-
gramming, volume 372 of LNCS, pages 1–17, Lon-
don, UK. Springer-Verlag.
Alon, U. (2007). Network motifs: theory and experimental
approaches. Nat. Rev. Genet., 8(6):450–461.
Emerson, E. A. (1990). Temporal and modal logic. In van
Leeuwen, J., editor, Handbook of Theoretical Com-
puter Science, Volume B: Formal Models and Semat-
ics (B), pages 995–1072. MIT Press.
Ito, S., Hagihara, S., and Yonezaki, N. (2014). A qualita-
tive framework for analysing homeostasis in gene net-
works. In Proceedings of the 5th International Con-
ference on Bioinformatics Models, Methods and Algo-
rithms (BIOINFORMATICS2014), pages 5–16.
Ito, S., Ichinose, T., Shimakawa, M., Izumi, N., Hagihara,
S., and Yonezaki, N. (2013a). Modular analysis of
gene networks by linear temporal logic. J. Integrative
Bioinformatics, 10(2).
Ito, S., Ichinose, T., Shimakawa, M., Izumi, N., Hagihara,
S., and Yonezaki, N. (2013b). Qualitative analysis
of gene regulatory networks using network motifs.
In Proceedings of the 4th International Conference
on Bioinformatics Models, Methods and Algorithms
(BIOINFORMATICS2013), pages 15–24.
Ito, S., Izumi, N., Hagihara, S., and Yonezaki, N. (2010).
Qualitative analysis of gene regulatory networks by
satisfiability checking of linear temporal logic. In Pro-
ceedings of the 10th IEEE International Conference
on Bioinformatics & Bioengineering, pages 232–237.
Mori, R. and Yonezaki, N. (1993). Several realizability con-
cepts in reactive objects. In Information Modeling and
Knowledge Bases IV, pages 407–424.
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
100

Pnueli, A. and Rosner, R. (1989). On the synthesis of a re-
active module. In POPL ’89: Proceedings of the 16th
ACM SIGPLAN-SIGACT symposium on Principles of
programming languages, pages 179–190, New York,
NY, USA. ACM.
Shimakawa, M., Hagihara, S., and Yonezaki, N. (2013).
Complexity of strong satisfiability problems for reac-
tive system specifications. IEICE Transactions, 96-
D(10):2187–2193.
Shimakawa, M., Hagihara, S., and Yonezaki, N. (2014).
Bounded strong satisfiability checking of reactive
system specifications. IEICE Transactions, 97-
D(7):1746–1755.
Vardi, M. Y. and Wolper, P. (1994). Reasoning about infinite
computations. Inf. Comput., 115:1–37.
ApproximateAnalysisofHomeostasisofGeneNetworksbyLinearTemporalLogicusingNetworkMotifs
101
