Combining Fisher Vectors in Image Retrieval Using Different Sampling

Techniques

Tom´as Mardones

, H´ector Allende

and Claudio Moraga

Department of Informatics, Universidad T´ecnica Federico Santa Mar´ıa, Valpara´ıso, Chile

European Centre for Soft Computing, Mieres, Spain

Keywords:

Fisher Vector, Image Retrieval, Feature Sampling Methods, Query by example.

Abstract:

This paper addresses the problem of content-based image retrieval in a large-scale setting. Most works in

the area sample image patches using an afﬁne invariant detector or in a dense fashion, but we show that

both sampling methods are complementary. By using Fisher Vectors we show how several sampling methods

can be combined in a simple fashion inquiring only in a small ﬁxed computational cost while signiﬁcantly

increasing the precision of the image retrieval system. As a second contribution, we show Fisher Vectors

using their variance component, normally ignored in image retrieval applications, have better performance

than their mean component under certain relevant settings. Experiments with up to 1 million images indicate

that the proposed method remains valid in large-scale image search.

1 INTRODUCTION

Content-based image retrieval (CBIR) is an important

area of research in Multimedia, since it is linked to

numerous image applications. Given a query image,

the problem consists in ﬁnding the most similar im-

ages in a database. In the last decade, the most popu-

lar method to face this problem with relative success

is the Bag of Features (BoF, Bag of Words or Bag

of Visual Words) representation (Nister and Stewe-

nius, 2006; Philbin et al., 2007). It can handle up

to a one million images database before the preci-

sion, time and memory constraints make it imprac-

tical for content-based image retrieval (J´egou et al.,

2012; Nister and Stewenius, 2006). BoF ﬁrst extracts

local features, called descriptors, from an image and

aggregates them into a histogram of “visual words”,

collecting 0-order statistics of the image descriptors.

To overcome the database size limitation, the

Fisher Vector (FV) (Perronnin and Dance, 2007; Per-

ronnin et al., 2010a) and Vector of Locally Aggre-

gated Descriptors (VLAD) (J´egou et al., 2012) image

representations replace the BoF histogram with de-

scriptor’s higher order statistics. The result in both

cases is a single vector which dimension is related

to the descriptor’s dimension and a single parameter.

In scenarios with more than one million images, us-

ing Scale InvariantFeature Transform (SIFT) descrip-

tors (Lowe, 2004), it has been shown dimensionality

reduction techniques can be used on FV and VLAD

leading to very compact representations that preserve

a high retrieval precision (J´egou et al., 2012; Per-

ronnin et al., 2010a; J´egou et al., 2011; Gong et al.,

2013).

The ﬁrst contribution of this work is a simple tech-

nique to combine Fisher Vectors based on descriptors

using different sampling methods, demonstrates un-

der what assumption it does work and gives an in-

tuitive insight on why combining “sparse” and dense

descriptions of the image does improve performance.

The second contribution is the elaboration of simple

tools that allow us to measure the quality and potential

of image representations combination methods. The

ﬁnal contribution corresponds to the reconsideration

of the use of the Fisher Vector’s variance component

in image retrieval (Perronnin et al., 2010a).

The remainder of this paper is organized as fol-

lows. In the next section the related work is reviewed,

next in section 3 brief review of the Fisher Vector rep-

resentation is provided. In section 4 our contributions

are described, and in section 5 their impact is eval-

uated through several experiments comparing them

with other works.

128

Mardones T., Allende H. and Moraga C..

Combining Fisher Vectors in Image Retrieval Using Different Sampling Techniques.

DOI: 10.5220/0005179201280135

In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 128-135

ISBN: 978-989-758-077-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

Different descriptor sampling techniques can lead

to distinct results, this is well known as there are

published works that report different results just by

changing the sampling method (Gordo et al., 2012).

On the other hand, combining sampling techniques

has been mostly overlooked in the context of CBIR,

as most related works use differentdescriptors and the

same sampling method (Gordo et al., 2012; Douze

et al., 2011; Perronnin et al., 2010b; Zheng et al.,

2014; Zhang et al., 2012; Wengert et al., 2011).

A group of recent works (Wengert et al., 2011;

Zhang et al., 2012; Zheng et al., 2014; Gordo et al.,

2012) combined colour and SIFT descriptors using

the same keypoints. In (Wengert et al., 2011), us-

ing the Bag of Features framework, a global colour

descriptor and a local counterpart that couples itself

with the SIFT features improving the precision of the

retrieval system (Hessian-afﬁne detector) were pro-

posed. In (Zheng et al., 2014) a multi-dimensional

inverted index to perform feature fusion in the BoF

framework is described, speciﬁcally of SIFT and

Colour Names (Shahbaz Khan et al., 2012) features

(Hessian-afﬁne detector). Gordo et al. (Gordo et al.,

2012) used the Fisher Kernel framework, concatenat-

ing two Fisher Vectors, one for SIFT features and the

other for colour features (both using dense sampling)

obtaining a signiﬁcant performance boost. None of

these works employ different sampling methods with

the same descriptor.

Douze et al. (Douze et al., 2011) combined several

different image representations to build a new repre-

sentation. Two of them were Fisher Vectors and a

histogram of oriented gradients, which used SIFT de-

scriptors extracted from Hessian-afﬁne interest points

and the histogram of oriented gradients (densely sam-

pled) respectively, therefore more than one sampling

technique was involved, but the complexity of the

model makes very hard to know if these elements did

improve the precision of the ﬁnal representation.

3 FISHER VECTOR IMAGE

REPRESENTATION

In this work we choose to work with Fisher Vectors

because they have analytical properties that are easier

to work with compared to VLAD and BoF (S´anchez

et al., 2013; J´egou et al., 2012). This representation is

based on the work of Jaakola and Haussler (Jaakkola

and Haussler, 1999) on Fisher kernels as a method to

compare aggregated data combining a generative and

discriminative approach. Perronnin and Dance (Per-

ronnin and Dance, 2007) adopted this framework,

building Fisher Vectors using SIFT descriptors mod-

elling their probability density function using a Gaus-

sian Mixture Model (GMM).

Let X = { x

, n = 1, ..., N} be the set of D-

dimensional local descriptors extracted from an im-

age with N descriptors. Let u

be a GMM, with

parameters λ = {w

, µ

, σ

, k = 1, ..., K} where K is

the number of Gaussians and w

, µ

and σ

stand

for the mixture weight, the mean vector and the di-

agonal covariance matrix of Gaussian k respectively.

The GMM models the generative process of any de-

scriptor,assuming independencybetween the descrip-

tors generation. The Fisher Vector mean and variance

component corresponding to the k-th Gaussian corre-

spond to:

√

∑

n=1

(k)



−µ



, (1)

√

∑

n=1

(k)

√



−µ

)

−1



. (2)

where γ

(k) corresponds to the soft assignment of de-

scriptor x

to the k-th Gaussian:

(k) =

)

∑

j=1

)

, (3)

with

∑

= 1, w

∈ [0, 1], i = {1, ··· , K} and n =

{1, ··· , N}.

The ﬁnal FV corresponds to the concatenation of

every component. To avoid the dependence on the

sample size the resulting FV is divided by the sam-

ple size N. Finally two usual normalization steps

are used: power normalization (Perronnin et al.,

2010a) and L

normalization (Perronnin et al., 2010a;

S´anchez et al., 2013). For further details the reader

may refer to (S´anchez et al., 2013).

4 COMBINING FISHER

VECTORS

SIFT descriptors extracted from regions found by

interest point detectors and those extracted by us-

ing dense sampling obey to different generation pro-

cesses. This occurs because most interest point detec-

tors center the descriptor in a high contrast area like

an edge and rotates it following some criteria to make

it invariant to several transformations. These charac-

teristics make these descriptors unlikely to describe

plain regions like the sky and to differentiate edges

with the same aspect, but different rotations in the

CombiningFisherVectorsinImageRetrievalUsingDifferentSamplingTechniques

129

same image. Therefore, the probability density func-

tions related to each set of descriptors are not equal,

so their respective associated GMMs and Fisher Vec-

tors are different.

In the following some simple tools that will be

useful to estimate the expected improvement of com-

bining different Fisher Vectors will be described. Af-

ter that we will provide a proof that shows concate-

nating Fisher Vectors can be a good solution under

certain circumstances.

4.1 Combination Performance Tools

A question that we asked ourselves was: how can we

know if Fisher Vectors based on descriptors sampled

differently can improve the precision of our informa-

tion retrieval system. For simplicity, let FV

and FV

be Fisher Vectors based on different sampling strate-

gies. A requisite is that they must have complemen-

tary information: if FV

obtains the same results as

in every query , it is unlikely that their combi-

nation would improve the performance of the system.

On the other hand, if by using FV

we obtain good re-

sults for a set of queries and FV

provides good results

in a complementary set where FV

does not perform

well, we may be able to combine both to increase the

precision of the system.

To test if two sampling methods are able to work

together we propose to use a histogram of the differ-

ence of average precision between both. Let AP

(q)

be the average precision for a query q using a Fisher

Vector with the s sampling strategy, the AP difference

between the use of sampling method 1 and 2 is:

dif f

(q) = AP

(q) −AP

(q). (4)

By using several queries it is possible to build a

histogram. To use this formula a benchmark dataset

is needed. This can be useful in some situations, be-

cause different sampling techniques are more appro-

priate for certain image types (e.g. nature, buildings,

sculptures, medical).

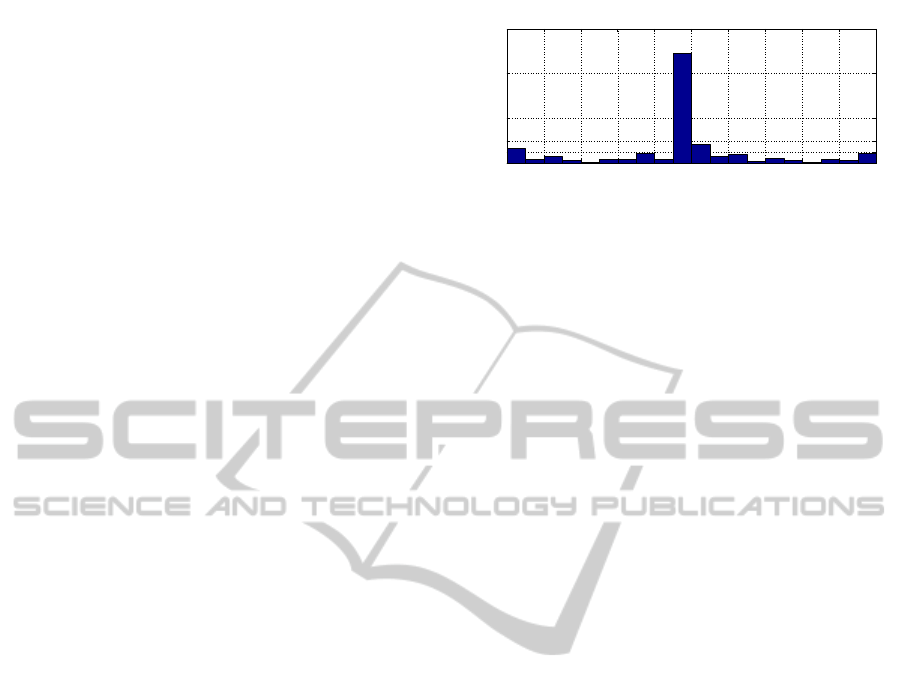
In Figure 1 it is shown the dif f

histogram ob-

tained from Fisher Vectors based on Hessian-afﬁne

and dense sampled descriptors respectively. It is im-

portant to notice that dif f

values lie in the [−1, 1]

range and to know what those values mean. Positive

valuesof Eq.4 representqueries where FV

performed

better than FV

. The most critical case is when FV

obtains the maximum AP 1 and FV

the minimum 0

and viceversa; in Figure 1 it is possible to see that this

accounts approximately for 10% of the queries. Neg-

ative values represent queries where FV

obtained a

better precision. Both positive and negative values of

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1

100

200

AP Difference Histogram (HA − D3)

diff

Queries

Figure 1: Average precision difference histogram from

Holidays dataset (500 queries). FVs are computed using

Hessian-afﬁne (HA) and dense (D3) sampled descriptors.

They are compared using Eq.(4) in each one of the 500

queries.

dif f

are necessary to know that two image repre-

sentations are complementary. Values near to zero of

Eq.4 represent querieswhere both methods performed

equally good or bad. For these queries the combina-

tion of different methods is less prone to obtain better

results.

It is also trivial to expand this tool to any image

representation, as long as it is possible to obtain the

average precision of a query.

To have a rough idea of the potential of combining

several representations, the oracle combination func-

tion max

is introduced. By oracle we mean this

function needs to know the AP obtained by every im-

age representation beforehand:

max

(q, R) = max

r∈R

(AP

(q)), (5)

where q is a query and R the set of possible image

representations. Using max

the mean AP (MAP) is

obtained by averaging max

(q, R) over all q.

Basically max

chooses the best representation

for each query procuring in the worst case the best

MAP obtained with an individual method.

The main goal of using this function is to know a

soft upper limit that we can reach by improving com-

bination methods. In section 5 max

will be used to

compare the results obtained by us.

4.2 Concatenation as a Combination

Method

Fisher Vectors concatenation is not a new idea, this

simple technique has been used before, mainly to

combine SIFT and color descriptors (Gordo et al.,

2012; Perronnin et al., 2010b), but its use has not been

justiﬁed, just has been part of the experimental setup.

In the remainder of this section we will show what

implicit assumption is done when Fisher Vectors are

concatenated.

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

130

Let u

∑

k=1

1,k

N (X

|µ

1,k

, σ

1,k

) be a mixture

of K Gaussians that models the X

descriptors prob-

ability distribution. On the other hand, let u

∑

k=1

2,k

N (X

|µ

2,k

, σ

2,k

) be another mixture of K

Gaussians representing the X

descriptors distribu-

tion. Without loss of generality we suppose that both

GMMs have the same number of Gaussians. X

and

are D dimensional and the covariance matrices of

and u

are diagonal following the Fisher Vector

framework.

Let X be a sample of X

and X

descriptors. If

we assume that the feature space spanned by X

very different from X

’s feature space, the following

should be true:

P(X ∈ X

) =

∑

k=1

2,k

N (X|µ

2,k

, σ

2,k

) ≈ 0 (6)

P(X ∈ X

) =

∑

k=1

1,k

N (X|µ

1,k

, σ

1,k

) ≈ 0 (7)

Equations 6 and 7 are only approximately zero

because X

and X

are in the same feature space.

This implies that any D-dimensional Gaussian has a

chance (in this case, near to zero) to generate a de-

scriptor, even when it is very far from its mean.

Leveraging the Gaussians independence, it is pos-

sible to join both mixtures, so one “big” mixture can

represent descriptors sampled from X

and X

u =

∑

k=1

N (X|µ

, σ

), (8)

where w

= [w

1,1

, ··· , w

1,K

, w

2,1

, ··· , w

2,K

]

= [µ

1,1

, ··· , µ

1,K

, µ

2,1

, ··· , µ

2,K

]

and

= [σ

1,1

, ··· , σ

1,K

, σ

2,1

, ··· , σ

2,K

]

If we use this mixture to compute a FV, using a

set X of N descriptors sampled from X

and X

, the

contribution of the ith Gaussian is depicted by Eq. 1

and 2. What changes is the γ

(k) function:

(k) =

N (x

|µ

, σ

)

∑

j=1

N (x

|µ

, σ

)

, (9)

with

∑

= 1, w

∈ [0, 1], i = {1, ··· , 2K} and n =

{1, ··· , N}.

If x

∈ X

and i = {1, ··· , K}, by making use of

Eq.6 we can approximate to zero all the terms related

to the u

Gaussians in the denominator of Eq.9. If

∈ X

, but i = {K + 1, ··· , 2K}, γ

(i) ≈ 0.

This implies that the Fisher Vector components

starting from the KD + 1 to the 2KD are approxi-

mately zero if the descriptors are sampled from X

Hence these descriptors can only contribute up to

the KD component. Analogously X

descriptors con-

tribute only in the KD+ 1, 2KD range of the FV.

Therefore if the X descriptors are divided into two

groups S

and S

depending on whether they belong

to X

or X

respectively and only the relevant Gaus-

sians are taken into account (e.g. u

for S

) the FV

can be decomposed as G

= [G

]

, where λ, λ

and λ

correspond to the parameters of u, u

and u

respectively. This vector is equivalent to the one we

obtain by concatenating the Fisher Vectors produced

independently using the initial Gaussian mixtures and

their respective descriptors.

When using PCA or other dimension reduction

technique on the concatenated Fisher Vectors, they

should target each FV individually to beneﬁt from the

knowledge that each FV comes from a different dis-

tribution.

One important advantage of using concatenated

Fisher Vectors, compared to the standard approach, is

that additional FVs provide extra information, while

there is only a ﬁxed computational cost overhead

when extracting additional features of the image and

the process of learning the parameters of an additional

GMM. In the next section it is shown that this method

can obtain better precision with the same memory us-

age.

5 EXPERIMENTS AND RESULTS

First the datasets and features used in the experiments

are described. Then results for individual and con-

catenated representations are provided for several set-

tings. Finally, the results are compared with other re-

cent works.

5.1 Datasets and Features

Datasets. The following two public benchmarks are

employed. INRIA Holidays (J´egou et al., 2008) con-

sists of 1,491 images of 500 scenes and objects. Each

scene / object has a query image and accuracy is mea-

sured as the Mean Average Precision (MAP) (Man-

ning et al., 2008). The University of Kentucky Bench-

mark (UKB) (Nister and Stewenius, 2006) consists of

10,200 images of 2,550 objects. Each image is used

alternatively as a query to search within the 10,200

images (including itself) and the performance is mea-

sured as 4×recall@4 (called Kentucky Score some-

times) averaged over the 10,200 queries. Therefore,

the score goes from 0 to four on this dataset.

The MIRFLICKR-25K dataset (Huiskes and Lew,

2008) is used to learn the GMM parameters and

the PCA matrices. For the large-scale experi-

ments reported in Section 5.5, the MIRFLICKR-1M

dataset images are used as distractors (Huiskes and

CombiningFisherVectorsinImageRetrievalUsingDifferentSamplingTechniques

131

1632641282565121K2K4K

0.3

0.35

0.4

0.45

0.5

0.55

0.6

0.65

0.7

Dimensions

MAP

MAP on Holidays

HesAff M

HesAff V

D1 M

D1 V

D3 M

D3 V

(a)

1632641282565121K2K4K8K16K

0.4

0.45

0.5

0.55

0.6

0.65

0.7

Dimensions

MAP

MAP on Holidays

D3 M K=32

D3 V K=32

D3 M K=64

D3 V K=64

D3 M K=256

D3 V K=256

(b)

Figure 2: Comparing the mean (M) and variance (V) component using different sampling techniques. (a) Hessian afﬁne based

sampling and dense sampling at two scale settings are tested . (b) The effect of using different number of Gaussians with 3

scale dense sampling.

Lew, 2008), except for the 25K images repeated in

MIRFLICKR-25K.

Features. 128-dimensional RootSIFT descriptors

(Arandjelovi´c, 2012) will be used as the local de-

scriptors as they have become an increasingly popu-

lar choice that performs better than SIFT in image re-

trieval. Three sampling methods are employed to ex-

tract descriptors in most experiments. The ﬁrst corre-

sponds to dense sampling: 24 pixel length square re-

gions every 8 pixels at 3 scales (D3). The second and

third sampling methods are the Hessian afﬁne (HA

or HesA) and Hessian Laplace (HL or HesL) interest

point detectors respectively (Tuytelaars and Mikola-

jczyk, 2008). Additionally two other interest point

based sampling methods were tested: Harris Afﬁne

(HarA) and Harris Laplace (HarL) (Tuytelaars and

Mikolajczyk, 2008), but the chosen two performed

better or similarly than the rest when concatenated

most of the time. Also 1 and 2 scales at dense sam-

pling were tested (D1 and D2 respectively), but using

3 scales works best when concatenated. The extracted

features are reduced to 64 dimensions with PCA. The

GMM used have 64 Gaussians. Each Fisher Vector

is computed separately, then power and L2 normal-

ized (J´egou et al., 2012; Perronnin et al., 2010b).

Fisher Vector’s mean component is used to repre-

sent the interest point based methods, but the variance

component is used for the dense sampling method as

it steadily attains better precision. To reduce Fisher

Vector dimensionality PCA is used. In the rest of

the section we will loosely refer to the Fisher Vectors

based on the descriptors sampled with the previously

mentioned methods as HA, HL and D3V (V stands

for variance component).

5.2 Fisher Vector Variance Component

and Different Sampling Methods

In most image retrieval works using Fisher Vectors

(Perronnin et al., 2010a; J´egou et al., 2012; Gong

et al., 2013; Gordo et al., 2012) the variance compo-

nent is ignored, since in (J´egou et al., 2012) it was

reported that using both component (using interest

point detectors) did not provide any signiﬁcant im-

provement over using just the mean component and

doubling the number of Gaussians. Even the “non-

probabilistic version” of the Fisher Vectors, VLAD

(J´egou et al., 2012), used mainly in image retrieval,

does not have a variance component. On the other

hand, S´anchez et al.(S´anchez et al., 2013) saw an

improvement in image classiﬁcation by using dense

sampling and the variance component for low val-

ues of K, compared to the use of the mean compo-

nent. This evidence was enough to experiment with

the variance component.

On Figure 2(a) it is possible to see that by us-

ing the Hessian afﬁne interest point detector and the

variance component, the performance degrades and is

quite unstable. This behaviour was similar in other

experiments when using the HesL, HarA and HarL

detectors. On the other hand, the results of using

dense sampling and the variance component is pos-

itive. The ﬁrst fact which is noticed is the superior

MAP obtained by the variance component after every

dimensionality reduction. And more importantly for

image retrieval is that it maintains its precision much

better at lower dimensionalities (at least when using

PCA).

S´anchez et al. (S´anchez et al., 2013) mentioned

that the difference between using the mean and vari-

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

132

Table 1: MAP on Holidays.

Detectors MAP / maxAP on Holidays

HA HL D3V D’ = 2048 D’ = 512 D’ = 256 D’ = 128 D’ = 32

× 64.4 63.1 60.5 57.9 49.4

× 67.0 65.2 63.1 59.5 51.8

× 65.3 64.6 64.0 63.2 56.7

× × 67.7 / 70.9 64.6 / 67.0 61.9 / 64.2 58.2 / 59.9 47.8 / 50.3

× × 74.3 / 77.4 73.7 / 75.2 71.6 / 74.0 69.7 / 71.6 58.7 / 59.1

× × 74.9 / 78.0 72.8 / 75.7 71.7 / 73.8 69.7 / 72.8 60.0 / 59.0

× × × 75.7 / 78.9 73.1 / 76.8 71.1 / 75.1 68.8 / 72.0 58.6 / 56.2

Table 2: KS on UKB.

Detectors KS / maxKS on UKB

HA HL D3V D’ = 2048 D’ = 512 D’ = 256 D’ = 128 D’ = 32

× 3.30 3.31 3.23 3.14 2.82

× 3.39 3.33 3.24 3.14 2.79

× 2.58 2.58 2.55 2.52 2.38

× × 3.50 / 3.53 3.40 / 3.42 3.32 / 3.34 3.22 / 3.23 2.77 / 2.73

× × 3.38 / 3.53 3.27 / 3.46 3.21 / 3.39 3.13 / 3.29 2.84 / 2.80

× × 3.30 / 3.53 3.17 / 3.43 3.10 / 3.35 3.02 / 3.25 2.76 / 2.77

× × × 3.53 / 3.62 3.41 / 3.52 3.34 / 3.45 3.25 / 3.33 2.88 / 2.69

ance component fades as the number of Gaussian in-

creases. In image retrieval it is very important to

know how does this behave as the dimensionality de-

creases. In Figure 2(b) it can be seen that by increas-

ing the number of Gaussians and using the mean com-

ponent the accuracy increment is substancial and it

does not show signs of stopping. Still, the accuracy

decreases at a faster pace and at lower dimensions the

representations using the variance component do have

the advantage and the K selection is less relevant. In

additional experiments it was observed that using in-

terest point detectors and the mean component of the

Fisher Vector is a better choice independently of the

K parameter.

5.3 Concatenate Fisher Vectors

In Table 1 and 2 we can see the results of the baseline

methods in both datasets against their combinations

at several memory usage scenarios. Note that 512

dimensions for a concatenated representation means

that each component uses 256 dimensions (if 2 repre-

sentations are being used). On Holidays the results

are promising, the combination of dense and inter-

est point sampling achieves a MAP increase, ranging

from 3.3% to 11.3%, using the same number of di-

mensions. The max

results are slightly better all the

time, except in some cases where the dimensionality

is very small and the precision of individual represen-

tations tend to get worse very fast.

On UKB we used the max

function, analog to

max

, but using the Kentucky Score (KS) instead of

AP. The results are much more mixed than in Hol-

idays. UKB is a dataset that focuses just on object

recognition, whereas Holidays is a mix of scenes,

landmarks and objects (simply holiday pictures). This

characteristic allows scale and rotation invariant de-

tectors to perform on UKB particularly well most of

the time. This is reﬂected on the fact that concate-

nating the FVs based on HA and HL sampling meth-

ods produce better results, even if they are methods

that detect similar regions. It is interesting to see that

max

has similar results for every dual combination,

this led us to think that despite the bad results of the

dense sampling method it does provide important in-

formation for certain queries. To test this idea, we

weighted the HA FV by two and concatenated it to the

D8 FV obtaining a score of 3.50 at 2048 dimensions.

Adding D8 to the mix of HL and HA representations

results in a slightly better representation for UKB, and

its difference with max

is still signiﬁcant, so bet-

ter results could be attained with a better combination

method.

When seeing the previous results, it is clear that

not every sampling method combination will be ad-

equate for every database, nevertheless the combina-

tion of HA, HL and D3V should be a good option

for most databases containing natural images, since it

was able to get good results on both benchmarks.

CombiningFisherVectorsinImageRetrievalUsingDifferentSamplingTechniques

133

1 2 5 10 25 50 100 250 500 1000

0.3

0.4

0.5

0.6

0.7

recall@K

recall@K on Holidays+1M

HA+HL+D3

(a)

2 5 10 25 50 100 250 500 1000

0.4

0.5

0.6

0.7

0.8

0.9

recall@K

recall@K on UKB+1M

HA+HL+D3

(b)

Figure 3: recall@K using almost 1M distractor images and 128-D representations.

5.4 Comparison with State of the Art

The results presented in Table 3 show how do other

state of the art methods perform against our method.

It was hard to decide which works to choose, since

normally incompatible methods are compared and in

this case most of the ideas presented in the other

works are applicable to our work or viceversa, since

they improve other points in the pipeline. We omitted

methods that used other descriptors (e.g. colour de-

scriptors), query expansion, spatial information and

any type of information that makes the representation

unsuitable for very large scale retrieval. The work of

J´egou et al.(J´egou et al., 2012) serves as a baseline

comparison, since it uses the most usual parameters

and processing steps. An important difference is that

we were not able to reproduce the results in UKB

using only the Hessian Afﬁne detector (see Table 2)

where J´egou et al. obtained a KS of 3.35 using the

full vector and 3.33 with a 128-D representation. The

main difference should be the training set used to ob-

tain the PCA matrix. The other works used for com-

parison improve the normalization step (Delhumeau

et al., 2013; Arandjelovi´c and Zisserman, 2013), the

learned visual words (Arandjelovi´c and Zisserman,

2013; J´egou and Chum, 2012) and the dimensional-

ity reduction (Delhumeau et al., 2013; J´egou et al.,

2012). In general, the results are very favorable for

our method in Holidays and in UKB it does a good

job at higher dimensions. Still it is fair to emphasize

the higher (but ﬁxed) computational overhead present

in our algorithm given the use of several detectors.

5.5 Large-scale Experiments

In Figure 3 the recall@K is shown for both datasets

using MIRFLICRK-1M distractor images. Following

the experimental setup of (Delhumeau et al., 2013;

Arandjelovi´c and Zisserman, 2013) for large-scale re-

trieval, 128-D representations were used (43-D×3 for

Table 3: Comparison with the State of the Art.

Method K D Holidays UKB

FV (J´egou et al., 2012) 64 8192 60.5 3.35

VLAD (J´egou et al., 2012) 64 8192 55.6 3.28

(Arandjelovi´c et al., 2013) 256 32768 64.6 -

(Arandjelovi´c et al., 2013) 256 128 62.5 -

(Delhumeau et al., 2013) 64 8192 65.8 -

(J´egou and Chum, 2012) 64 128 61.4 3.36

HA+HL+D3V 64 8192 75.4 3.53

HA+HL+D3V 64 128 68.8 3.25

the concatenated one). The proposed method obtains

a remarkable advantage on both datasets, disregard-

ing the irregular performance of some sampling meth-

ods. The biggest advantage is obtained when using a

K from 5 to 50, a very important segment for image

retrieval engines. The MAP for Holidays+1M was

56.5% for the proposed method, 12.3% less than the

initial MAP, compared to the 15.4% average loss of

the individual methods. On UKB+1M the KS was

3.09 for the proposed method, 0.16 less than than the

initial KS, compared to the 0.34 average loss of the

individual representations.

6 CONCLUSIONS AND FUTURE

WORK

In this work it was primarily shown that the combi-

nation of different descriptor sampling methods can

be very beneﬁcial in the task of image retrieval. To

justify the use of concatenation as a combination

method, some of its theoretical implications were

treated in the case of using Fisher Vectors. Also a

couple of simple tools were presented to help with

the task of analyzing the potential of coupling pairs

of representations and to have an idea of the perfor-

mance attainable when combining a group of repre-

sentations. Furthermore it was shown that the vari-

ance component of Fisher Vectors can be very infor-

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

134

mative depending on the descriptors probability dis-

tribution.

The results obtained encourage further work in

this direction. Concatenation is a very simple and fast

(practically zero cost) method of combination, but it

does not make any distinction between the different

representations involved, even if they perform badly

with certain kind of images. A deeper research on

ensemble methods could prove to be fruitful.

Other way to look the results is that there are sev-

eral families of descriptors that can contribute with

rich information, but the a speciﬁc sampling method

detects only a few of these families. To identify

these sets of complementary descriptors and to de-

velop methods to extract them is another rich ﬁeld of

research.

ACKNOWLEDGEMENTS

This work was supported by the following research

and fellowship grants: Fondecyt 1110854, DGIP-

UTFSM, MECESUP and CONICYT. The work of C.

Moraga was partially supported by the Foundation for

the Advance of Soft Computing, Mieres, Spain, and

by the CICYT Spain, under project TIN 2011-29827-

C02-01.

REFERENCES

Arandjelovi´c, R. (2012). Three things everyone should

know to improve object retrieval. In Proc. CVPR,

pages 2911–2918.

Arandjelovi´c, R. and Zisserman, A. (2013). All about

VLAD. In Proc. CVPR, pages 1578–1585.

Delhumeau, J., Gosselin, P.-H., J´egou, H., and P´erez, P.

(2013). Revisiting the VLAD image representation.

In Proc. ACM Int. Conf. on Multimedia, pages 653–

656.

Douze, M., Ramisa, A., and Schmid, C. (2011). Combin-

ing attributes and Fisher vectors for efﬁcient image re-

trieval. In Proc. CVPR, pages 745–752.

Gong, Y., Lazebnik, S., Gordo, A., and Perronnin, F.

(2013). Iterative quantization: A procrustean ap-

proach to learning binary codes for large-scale image

retrieval. Pattern Analysis and Machine Intelligence,

35(12):2916–2929.

Gordo, A., Rodriguez-Serrano, J. A., Perronnin, F., and Val-

veny, E. (2012). Leveraging category-level labels for

instance-level image retrieval. In Proc. CVPR, pages

3045–3052.

Huiskes, M. J. and Lew, M. S. (2008). The MIR Flickr

retrieval evaluation. In Proc. ACM Int. Conf. on Mul-

timedia Information Retrieval, pages 39–43.

Jaakkola, T. S. and Haussler, D. (1999). Exploiting gen-

erative models in discriminative classiﬁers. In Proc.

Conf. on Advances in Neural Information Processing

Systems II, pages 487–493.

J´egou, H. and Chum, O. (2012). Negative evidences and

co-occurrences in image retrieval: the beneﬁt of PCA

and whitening. In Proc. ECCV, pages 774–787.

J´egou, H., Douze, M., and Schmid, C. (2008). Hamming

embedding and weak geometric consistency for large

scale image search. In Proc. ECCV, volume I, pages

304–317.

J´egou, H., Douze, M., and Schmid, C. (2011). Prod-

uct quantization for nearest neighbor search. Pattern

Analysis and Machine Intelligence, 33(1):117–128.

J´egou, H., Perronnin, F., Douze, M., S´anchez, J., P´erez, P.,

and Schmid, C. (2012). Aggregating local image de-

scriptors into compact codes. Pattern Analysis and

Machine Intelligence, pages 1704–1716.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2):91–110.

Manning, C. D., Raghavan, P., and Schtze, H. (2008). In-

troduction to Information Retrieval. Cambridge Uni-

versity Press, New York.

Nister, D. and Stewenius, H. (2006). Scalable recognition

with a vocabulary tree. In Proc. CVPR, pages 2161–

2168.

Perronnin, F. and Dance, C. R. (2007). Fisher kernels on

visual vocabularies for image categorization. In Proc.

CVPR, pages 1–8.

Perronnin, F., Liu, Y., Snchez, J., and Poirier, H. (2010a).

Large-scale image retrieval with compressed Fisher

vectors. In Proc. CVPR, pages 3384–3391.

Perronnin, F., S´anchez, J., and Mensink, T. (2010b). Im-

proving the Fisher kernel for large-scale image classi-

ﬁcation. In Proc. ECCV, pages 143–156.

Philbin, J., Chum, O., Isard, M., Sivic, J., and Zisserman, A.

(2007). Object retrieval with large vocabularies and

fast spatial matching. In Proc. CVPR, pages 1–8.

S´anchez, J., Perronnin, F., Mensink, T., and Verbeek, J.

(2013). Image classiﬁcation with the Fisher vector:

Theory and practice. International Journal of Com-

puter Vision, 105(3):222–245.

Shahbaz Khan, F., Anwer, R., van de Weijer, J., Bagdanov,

A., Vanrell, M., and Lopez, A. (2012). Color attributes

for object detection. In Proc. CVPR, pages 3306–

3313.

Tuytelaars, T. and Mikolajczyk, K. (2008). Local invariant

feature detectors: A survey. Foundations and Trends

in Computer Graphics and Vision, 3(3):177–280.

Wengert, C., Douze, M., and J´egou, H. (2011). Bag-of-

colors for improved image search. In ACM Multime-

dia, pages 1437–1440.

Zhang, S., Yang, M., Cour, T., Yu, K., and Metaxas, D.

(2012). Query speciﬁc fusion for image retrieval. In

Proc. ECCV, pages 660–673.

Zheng, L., Wang, S., Zhou, W., and Tian, Q. (2014). Bayes

merging of multiple vocabularies for scalable image

retrieval. In Proc. CVPR, pages 1963–1970.

CombiningFisherVectorsinImageRetrievalUsingDifferentSamplingTechniques

135