
Towards Pose-free Tracking of Non-rigid Face using Synthetic Data
Ngoc-Trung Tran
1,2
, Fakhreddine Ababsa
2
and Maurice Charbit
1
1
LTCI, Telecom ParisTECH, 37-39 rue Dareau, 75014 Paris, France
2
IBISC, University of Evry, 40 rue du Pelvoux, 91020 Evry, France
Keywords:
3D Face Tracking, 3D Pose Tracking, Rigid Tracking, Non-rigid Tracking, Face Matching, Synthesized Face,
Face Matching.
Abstract:
The non-rigid face tracking has been achieved many advances in recent years, but most of empirical exper-
iments are restricted at near-frontal face. This report introduces a robust framework for pose-free tracking
of non-rigid face. Our method consists of two phases: training and tracking. In the training phase, a large
offline synthesized database is built to train landmark appearance models using linear Support Vector Machine
(SVM). In the tracking phase, a two-step approach is proposed: the first step, namely initialization, benefits
2D SIFT matching between the current frame and a set of adaptive keyframes to estimate the rigid parame-
ters. The second step obtains the whole set of parameters (rigid and non-rigid) using a heuristic method via
pose-wise SVMs. The combination of these aspects makes our method work robustly up to 90
◦
of vertical
axial rotation. Moreover, our method appears to be robust even in the presence of fast movements and track-
ing losses. Comparing to other published algorithms, our method offers a very good compromise of rigid
and non-rigid parameter accuracies. This study gives a promising perspective because of the good results in
terms of pose estimation (average error is less than 4
o
on BUFT dataset) and landmark tracking precision (5.8
pixel error compared to 6.8 of one state-of-the-art method on Talking Face video). These results highlight the
potential of using synthetic data to track non-rigid face in unconstrained poses.
1 INTRODUCTION
Non-rigid face tracking is an important topic, which
has been having a great attention since last decades.
It is useful in many domains such as: video mon-
itoring, human computer interface, biometric. The
problem gets much more challenging if occurring out-
of-plane rotation, the illumination changes, the pres-
ence of many people, or occlusions. In our study, we
propose an approach to track non-rigid face at out-of-
plane rotation, even the profile face. In other words,
our method gets involved in the estimation of six rigid
face parameters, namely the 3D translation and the
three axial rotations
1
, and non-rigid parameters at the
same time.
For non-rigid face tracking, a set of landmarks
are considered as the face shape model. Since the
pioneer work of (Cootes et al., 2001), it is well-
known that Active Appearance Model (AAM) pro-
vides an efficient way to represent and track frontal
faces. Many works (Xiao et al., 2004; Gross et al.,
1
In the literature, the terms Yaw (or Pan), Pitch (or Tilt),
and Roll are adopted for the three axial rotations.
2006; Matthews and Baker, 2004) have suggested im-
provements in terms of fitting accuracy or profile-
view tracking. Constrained Local Model (CLM) has
been proposed by (Cristinacce and Cootes, 2006) that
consists of an exhaustive local search around land-
marks constrained by a shape model. (Wang et al.,
2008; Saragih et al., 2011) both improvedthis method
in terms of accuracy and speed; more specifically,
(Saragih et al., 2011) can track single face with verti-
cal rotation up to 90
◦
in well-controlled environment.
The Cascaded Pose Regression (CPR), which is firstly
proposed by (Dollar et al., 2010), has recently shown
remarkable performance (Cao et al., 2012; Xiong and
la Torre Frade, 2013). This method shows the high
accuracy and real-time speed, merely it is restricted at
the near-frontal face tracking. Most of the methods
work at constrained views because of two reasons:
i) The acquisition of ground-truth for unconstrained
views is really expensive in practice and ii) how to
handle the hidden landmarks on invisible side is hard.
The literature also mentioned other face models
such as: cylinder (Cascia et al., 2000; Xiao et al.,
2003; Morencyet al., 2008), ellipsoid (An and Chung,
37
Tran N., Ababsa F. and Charbit M..
Towards Pose-free Tracking of Non-rigid Face using Synthetic Data.
DOI: 10.5220/0005179300370044
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 37-44
ISBN: 978-989-758-077-2
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2008) or mesh (Vacchetti et al., 2004). Most of these
methods can estimate the three large rotations even on
the profile-view, but it is worth noting that they handle
with rigid rather than non-rigid facial expression. On
the other hand, the popular 3D Candide-3 model has
been defined to manage rigid and non-rigid parame-
ters. (Str¨om, 2002) used Kalman Filter to the interest
points in a video sequence based on the adaptive ren-
dered keyframe, and this work is semi-automatic and
is insufficient to work in quick movement. (Chen and
Davoine, 2006) used Mahalanobis distances of local
features with the constraint of the face model, to cap-
ture both rigid and non-rigid head motions. (Alonso
et al., 2007) learned a linear model between model
parameters and the face’s appearance. These methods
poorly works on profile-view. (Lefevre and Odobez,
2009) extended Candide face to work with the pro-
file, but their objective function, combining structure
and appearance features with dynamic modeling, ap-
pears to slowly converge due to the high dimensional-
ity. (Tran et al., 2013) proposed an adaptive Bayesian
approach to track principal components of landmark
appearance. Their algorithm appears to be robust for
tracking landmarks, but unable to recover when track-
ing is lost. Let us notice that these methods use the
synthetic database to train tracking models.
A face tracking framework is robust if it can oper-
ate with a wide range of pose views, face expression,
environmental changes and occlusions, and also have
recovering capability. In (Cascia et al., 2000; Xiao
et al., 2003), the authors utilized dynamic templates
based on cylinder model in order to handle with light-
ing and self-occlusion. Local features can be consid-
ered (Saragih et al., 2011; Xiong and la Torre Frade,
2013), since local descriptors are not much affected
by facial expressions and self-occlusion. In order to
have recovering capability, tracking-by-detection or
wide baseline matching (Vacchetti et al., 2004; Jang
and Kanade, 2008; Wang et al., 2012) have been ap-
plied. The primary idea is to match the current frame
with preceding-stored keyframes. The matching is
sufficient to fast movements, illumination, and able
to recover the lost tracking. However, the match-
ing is only suitable to work with rigid parameters;
moreover, these methods degrade when the number
of keypoints detected on the face is not enough. Re-
cently, (Asteriadis et al., 2014) propose the combina-
tion of traditional tracking techniques and deep learn-
ing to have a proficient performance of pose tracking.
Many commercial products also exist, i.e. (FaceAPI,
), which shows effect results in pose and face anima-
tion tracking, but this product needs to work in con-
trolled environments of illumination and movements.
In addition, it has to wait for the frontal view to re-
initialize the model when the face is lost.
In this paper, our contribution is two-folds: (i) us-
ing a large offline synthetic database to train tracking
models, (ii) proposing a two-step tracking approach
to track non-rigid face. These points are immediately
introduced in more detail. Firstly, a large synthesized
database is built to avoid the expensive and time-
consuming manual annotation. To the best of our
knowledge, although there were some papers worked
with the synthetic data (Gu and Kanade, 2006; Alonso
et al., 2007; Su et al., 2009), our paper is the first study
that investigates the large offline synthetic dataset for
the free-pose tracking of non-rigid face. Secondly, the
tracking approach consists of two steps: a) The first
step benefits 2D SIFT matching between the current
frame and some preceding-stored keyframes to esti-
mate only rigid parameters. By this way, our method
is sustainable to fast movement and recoverable in
terms of lost tracking. b) The second step obtains
the whole set of parameters (rigid and non-rigid) by
a heuristic method using pose-wise SVMs. This way
can efficiently align a 3D model into the profile face
in similar manner of the frontal face fitting. The com-
bination of three descriptors is also considered to have
better local representation.
The remaining of this paper is organized as fol-
lows: Section 2 describes the face model and the used
descriptors. Section 3 discusses the pipeline of the
proposed framework. Experimental results and anal-
ysis are presented in Section 4. Finally, we provide in
Section 5 some conclusions and further perspectives.
2 FACE REPRESENTATION
2.1 Shape Representation
Candide-3, initially proposed by (Ahlberg, 2001), is
a popular face model managing both facial shape and
animation. It consists of N = 113 vertices represent-
ing 168 surfaces. If g ∈ R
3N
denotes the vector of
dimension 3N, obtained by concatenation of the three
components of the N vertices, the model writes:
g(σ, α) =
g+ Sσ + Aα (1)
where
g denotes the mean value of g. The known ma-
trices S ∈ R
3N×14
and A ∈ R
3N×65
are Shape and An-
imation Units that control respectively shape and an-
imation through σ and α parameters. Among the 65
components of animation control α, 11 ones are asso-
ciated to track eyebrows, eyes and lips. Rotation and
translation also need to be estimated during tracking.
Therefore, the full model parameter, denoted θ, has
17 dimensions: 3 dimensions of rotation (r
x
, r
y
, r
z
), 3
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
38
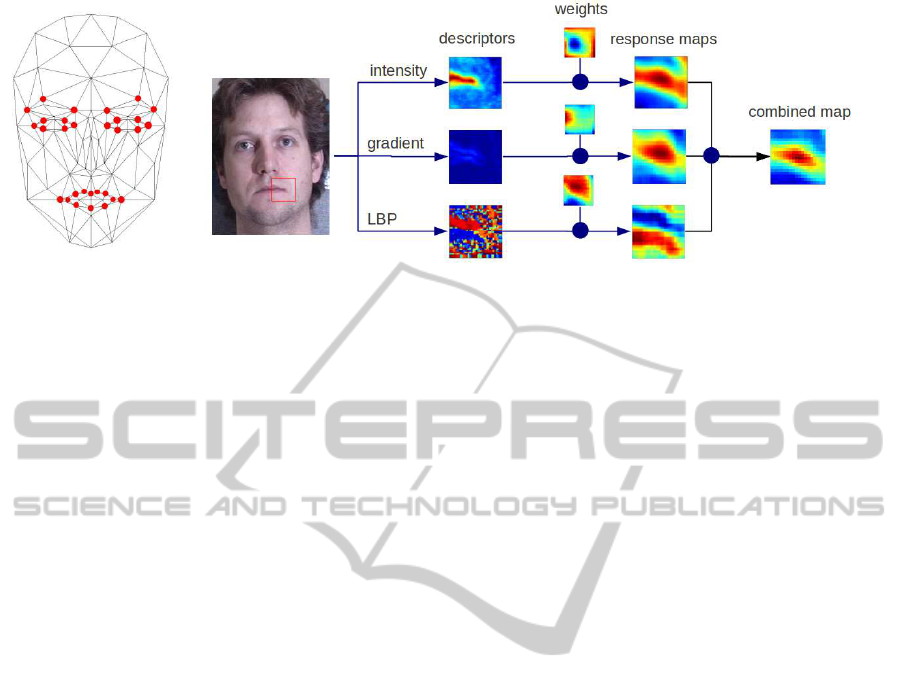
Figure 1: (a) The Candide-3 model with facial points in our method. (b) The way to compute the response map at the mouth
corner using three descriptors via SVM weights.
dimensions of translation (t
x
,t
y
,t
z
) and 11 dimensions
of animation r
a
: θ = [r
x
r
y
r
z
t
x
t
y
t
z
r
a
]
T
. Notice that
both σ and θ are estimated at first frame, but only θ is
estimated at next frames because we assume that the
shape parameter does not change.
2.2 Projection
We assume the perspective projection, in which the
camera calibration has been obtained from empirical
experiments. In our case, the intrinsic camera matrix
K = [ f
x
, 0, c
x
;0, f
y
, c
y
;0, 0, 1], where the focal length
of camera f
x
= f
y
= 1000 pixels and the coordinates
of a camera’s principal point (c
x
, c
y
) as a center of
the 2D video frame. The such focal length is defined
because it is shown in (Aggarwal et al., 2005) that the
focal length does not require to be accurately known
if the distance between the 3D object and camera is
much larger than the 3D object depth. Notice that
because of the perspective projection assumption, the
depth t
z
is directly related to scale parameter.
2.3 Appearance Representation
The facial appearance is represented by a set of 30
landmarks (Fig. 1). The local patch of a landmark
is described by three local descriptors: intensity, gra-
dient and Local Binary Patterns (LBP) (Ojala et al.,
1996) because the combination of multiple descrip-
tors are more discriminative and robust. This combi-
nation is fast enough if using linear SVM like (Wang
et al., 2008). The patch size is 15 × 15 in our study.
3 OUR METHOD
We present the framework into three sub-sections:
(i) the model training from synthesized dataset, (ii)
the robust initialization using wide baseline matching,
and (iii) the fitting strategy using pose-wise SVMs.
3.1 Model Training From Synthesized
Data
We consider the synthesized data for the training be-
cause of some reasons: (i) Most of available datasets
were built for frontal face alignment (Koestinger
et al., 2011). The others contain profile information
such as ALFW (Koestinger et al., 2011), Multi-PIE
(Gross et al., 2010), but the range of Pitch or Roll
are restricted. In addition, the number of landmarks
of frontal and profile faces is different. That makes a
gap, how to track from frontal to profile faces (ii) The
campaign of ground-truthfor buildinga new dataset is
very expensive and (iii) The hidden landmarks could
be localized in synthesized dataset, so the gap be-
tween frontal and profile tracking could be bridged.
The training process is shown in Fig. 2. At first,
we select 143 frontal images (143 different subjects)
from Multi-PIE. We then align 3D face model into
the known landmarks of each image by POSIT (De-
menthon and Davis, 1995) and warp the image tex-
ture to the model. Afterwards, rendering is deployed
to generate a set of synthesized images of different
poses. Finally, all synthesized images are clustered
into pose-wise groups before extracting local features
and training landmark models by linear SVM clas-
sifiers. In terms of rendering, we only consider the
three rotations to generate synthesize data. Indeed,
we can assume that the translation parameters do not
considerably affect the facial appearance. Because of
storage and computational problems, the data are ren-
dered in followingranges: 15 ofYaw∈ [−70 : 10 : 70],
11 of Pitch ∈ [−50 : 10 : 50], 7 of Roll ∈ [−30 : 10 :
30]. The empirical experiments show that the men-
tioned ranges are sufficient for a robust tracking.
Linear SVMs are used for landmark model train-
TowardsPose-freeTrackingofNon-rigidFaceusingSyntheticData
39

Figure 2: From left to right of training process: 143 frontal images, landmark annotation and 3D model alignment, synthesized
images rendering, and pose-wise SVMs training.
ing because of its computational efficiency (Wang
et al., 2008), and the combination of three de-
scriptors (Section 2.3) makes robust response maps
more robust. Because of large pose variation of
the dataset, the pose-wise SVMs are trained as fol-
lows. The total rendered images are splitted into 1155
(15(Yaw) × 11(Pitch) × 7(Roll)) pose-wise groups
(143 images/group). Each group is used to train 90
pose-wise linear SVMs (30 landmarks × 3 descrip-
tors) in similar manner of (Wang et al., 2008). So,
the total of 103950 classifiers (namely ζ) needs to be
trained. In the other words, let us denote C
x,y,z
∈ ζ
is one classifier that is trained on the specific pose x
(∈ 1155 poses), the landmark id y (∈ [1, .., 30]) and
the descriptor type z (∈ [intensity, gradient, LBP]).
With the given descriptor of local region φ
z
, C
x,y,z
(φ
z
)
returns the map of confidence levels, called response
map. This map is the confidence matrix of how cor-
rect the landmark may be localized. See Fig. 1. The
number of classifiers seems too great, but it is appli-
cable in practice because this training is once offline
and just a few of classifier is employed at each time
in tracking. In order to train a such big number of lin-
ear SVM classifiers, a very fast linear SVM, libLinear
(Fan et al., 2008), is one suitable tool.
3.2 Robust Initialization
In non-rigid face tracking, the aligned model from the
previous frame was usually used as the initialization
for the current frame. This initialization is hard to
robustly work with fast motions. Some others, e.g.
(Saragih et al., 2011), (in the implementation) adap-
tively localized the current face position via the max-
imum response of template matching (Lewis, 1995).
However, the false positive detection can happen, and
the recovery in terms of lost tracking is impossible if
the face detection is not involved. In fact, the informa-
tion from some previous frames could provide a more
robust initialization. (Wang et al., 2012) showed im-
pressive results of pose tracking by matching via key-
point learning. Yet, we propose to use the simpler
strategy for initialization. Our method uses the SIFT
matching like (Jang and Kanade, 2008) and estimate
the rigid parameters closely to (Vacchetti et al., 2004).
It is sustainable enough to fast motions and provides
the accurate recovery before fitting the face model by
pose-wise SVMs in the next step.
First of all, 2D SIFT points are detected. We base
on the projections from the 3D model of the keyframe
k onto the 2D current frame t to estimate the rotation
and translation (rigid parameters). Let us denote n
k
and n
t
are the numbers of SIFT points detected re-
spectively on a keyframe k and a frame t > k, and
l
k
=
l
0
k
, l
1
k
, ..., l
n
k
k
and
l
t
=
l
0
t
, l
1
t
, ..., l
n
t
t
(2)
are their respective locations. Let define the 3D
points L
k
, which associated with the 2D points l
k
,
are the intersections between the 3D model and the
straight lines passing through the projection center of
the camera and the 2D locations l
k
. Because some
points can be invisible (that are ignored), the number
of L
k
could be different to m. If R
k,t
and T
k,t
denote re-
spectively the rotation and translation from frame k to
frame t, we can write that, for i = 1 to m, the predicted
i-th point at frame t could be written:
b
l
i
t
= KΦ(L
i
k
) where Φ(L
i
k
) = (R
k,t
◦ T
k,t
)L
i
k
(3)
where ◦ denotes the composition operator and K
is the intrinsic camera matrix. To determine R
k,t
and
T
k,t
, we use the following least squares algorithm:
{
ˆ
R
k,t
,
ˆ
T
k,t
} = arg min
R
k,t
,T
k,t
∑
l
j
k
⇆l
i
t
l
i
t
− KΦ(L
j
k
)
2
(4)
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
40

where
∑
l
j
k
⇆l
i
t
denotes the sum over the couples
(i, j) obtained by matching RANSAC algorithm of
(Fischler and Bolles, 1981) between the keyframe k
and the current frame t. This transformation is de-
noted l
j
k
⇆ l
i
t
. Before using RANSAC, we use the
Flann matcher in both directions (from the keyframe
k to the current frame t and vice versa) and return
their intersection as a result. Finally, the optimiza-
tion of the expression (4) is effected numerically via
the Levenberg-Marquardt algorithm.
The 2D face region and its rigid parameters, 2D
and 3D corresponding points, and the value of objec-
tive function (5) (Section 3.3) are saved as a keyframe
while tracking. To estimate rigid parameters, the
current frame t is matched to all preceding-stored
keyframes to select a candidate keyframe k. The can-
didate keyframe is the keyframe that have the max-
imum number of matching points with the current
frame (after RANSAC). This number should be larger
than a given threshold; otherwise, we estimate param-
eters using Harris points tracked by KLT from the
previous frame. The current frame is registered as
a keyframe into the set of keyframes if one of three
residuals (Yaw, Pitch or Roll), between the current
frame and this direction of the whole set of preceding
keyframes, is larger than 10
◦
. The first keyframe is
fixed and other keyframes can be updated. The up-
dating happens if the keyframe is candidate keyframe
and its value of (5) is bigger than current frame’s. To
make sure unless bad keyframes were registered, we
detect the face position parallelly by the face detector
and compute the distance between this position and
where is detected by matching. The keyframe used
for matching (candidate keyframe) is withdrawn from
the set of keyframes if this distance is too large. It is
worth noting the face model aligning on first frame is
considered as the first keyframe. Our method is fully
automatic, and no manual keyframe is selected before
tracking the sequence.
3.3 Fitting via Pose-Wise Classifiers
The previous step provides precisely the initial pose
of face model. This pose permits to determine which
pose-wise SVMs among the set of SVMs (ζ) should
be chosen for fitting. Assume that θ
r
is the rotation
components of the current model parameter θ that are
estimated after the initialization step. m groups of
SVMs (C
θ
i
,y,z
, i = 1, ..., m), where θ
i
is m nearest val-
ues of θ
r
, are chosen for fitting. m = 4 obtains the best
performance in our empirical experiments. Given the
θ parameter of 3D face model, x
k
(θ) denotes the pro-
jection of the k-th landmark on the current frame. The
response map of x
k
(θ) is computed independently
by each group as follows: Three local descriptors
φ
z
, z ∈ [intensity (gray), gradient (grad), LBP (lbp)],
are extracted around the landmark k-th. The com-
bined response map is the element-by-element mul-
tiplication of response maps (normalized into [0, 1])
that are computed independently by descriptors: w =
C
θ
i
,k,gray
(φ
gray
).∗C
θ
i
,k,grad
(φ
grad
).∗C
θ
i
,k,lbp
(φ
lbp
), see
Fig. 1. This final combined response map is applied
to detect candidates of landmark location. The same
procedure is applied for all landmarks. It is worth not-
ing that the face is normalized to one reference face
before extracting feature descriptors.
If picking up the highest score position as the can-
didate of k-th landmark, m candidates have to be con-
sidered (from m pose-wise SVMs C
θ
i
,k,z
,i = 1, ..., m).
However, the highest score is not always the best one
through observations and other peaks are probably the
candidates as well. By this investigation, we keep
more than one candidate (if it is local peak and its
score is bigger than 70% of the highest one) before
determining the best by shape constraints. The set of
candidates of k-th landmark detected by m classifiers
C
θ
i
,k,z
are merged together. Let us denote Ω
k
is this
merged set of candidates. The rigid and non-rigid pa-
rameters can be estimated via the objective function:
b
θ = arg min
p
k
∈Ω
k
,θ
n
∑
k=1
w
k
kx
k
(θ) − p
k
k
2
2
(5)
where x
k
(θ) is the projection of kth landmark cor-
responding to θ. Meanwhile, the position p
k
∈ Ω
k
with the confidence w
k
(from its response map) to be
the candidate of the kth landmark. The optimization
problem in Eq. 5 is combinatorial. In our work, we
propose a heuristic method, which is based on ICP
(Iterative Closest Points) (Besl and McKay, 1992) al-
gorithm, to find the solution. The proposed approach
consists of two iterative sub-steps: i) looking for the
closest candidate p
k
from x
k
(θ), and ii) estimating the
update ∆θ using gradient method. As represented in
Algorithm 1. The update ∆θ can be computed via
the approximation of Taylor expansion that was men-
tioned similarly in (Saragih et al., 2011), where J
k
is
the Jacobian matrix of the kth landmark.
∆θ =
n
∑
k=1
w
k
J
T
k
J
k
!
−1
n
∑
k=1
w
k
J
T
k
(p
k
− x
k
(θ))
!
(6)
4 EXPERIMENTAL RESULTS
We adopted the Boston University Face Track-
ing (BUFT) database of (Cascia et al., 2000) and
TowardsPose-freeTrackingofNon-rigidFaceusingSyntheticData
41

Figure 3: Our two-step approach from the frame t to t + 1. First step uses SIFT matching to estimate the rigid parameters.
Second step uses pose-wise SVMs to re-estimate rigid and non-rigid paramters. The aligned current frames are stored as
keyframes if they satisfy some given conditions.
Algorithm 1: The fitting algorithm.
INPUT: n sets of Ω
k
and the θ at previous frame.
OUTPUT: θ at current frame.
1: repeat
2: Localizing 2D coordinate projection of land-
marks x
k
(θ), k = 1, .., n.
3: Looking v = 4 nearest candidates p
k
from
x
k
(θ) in Ω
k
.
4: Selecting the candidate p
k
from v ones that has
highest SVM score w
k
.
5: Computing Jacobian matrices J
k
at θ.
6: Computing updates △θ using {Eqn. 6}.
7: θ ← θ+ △θ
8: until θ converged.
Talking Face video
2
to evaluate the precision of
pose estimation and landmark tracking respectively.
Some VidTimid videos of (Sanderson, 2002), and
Honda/UCSD of (Lee et al., 2003) are also used to
investigate profile-face tracking capability.
BUFT: The pose ground-truth is captured by mag-
netic sensors “Flock and Birds” with an accuracy of
less than 1
o
. The uniform-light set, which is used to
evaluate, has a total of 45 video sequences (320×240
resolution) for 5 subjects (9 videos per subject) with
available ground-truth of pose Yaw (or Pan), Pitch
(or Tilt), Roll. The precision is measured by Mean
Absolute Error (MAE) of three directions between
the estimation and ground-truth over tracked frames:
E
yaw
, E
pitch
, E
roll
and E
m
=
1
3
E
yaw
+ E
pitch
+ E
roll
where E
yaw
=
1
N
s
∑
|θ
i
yaw
−
ˆ
θ
i
yaw
| (similarly for the
Pitch and Roll). N
s
is the number of frames and
2
http://www-prima.inrialpes.fr/FGnet/data/01-
TalkingFace/talking face.html
Table 1: The pose precision of our method and state-of-the-
art methods on uniform-light set of BUFT dataset.
Approach E
yaw
E
pitch
E
roll
E
m
(Wang et al., 2012) 3.8 2.7 1.9 2.8
(Xiao et al., 2003) 3.8 3.2 1.4 2.8
(Lefevre and Odobez, 2009) (+) 4.4 3.3 2.0 3.2
(Jang and Kanade, 2008) (*) 4.6 3.7 2.1 3.5
(Asteriadis et al., 2014) (*) 4.3 3.8 2.6 3.5
(Morency et al., 2008) (*) 5.0 3.7 2.9 3.9
(Saragih et al., 2011) (*,+) 4.3 4.8 2.6 3.9
(Tran et al., 2013) (+) 5.4 3.9 2.4 3.9
Our method (*,+) 5.0 4.5 2.2 3.9
θ
i
yaw
,
ˆ
θ
i
yaw
are the estimated value and ground-truth of
Yaw respectively.
Since BUFT videos have low resolution and the
number of SIFT points is often not enough to apply
the matching, our result (Table 1) is still comparable
to state-of-the-art methods. Our method achieves the
same mean error E
m
as (Saragih et al., 2011; Morency
et al., 2008; Tran et al., 2013), but worse than (Xiao
et al., 2003; Lefevre and Odobez, 2009; Jang and
Kanade, 2008; Wang et al., 2012; Asteriadis et al.,
2014). With the use of offline training of synthesized
data, the result is promising. The algorithm is bet-
ter than (Tran et al., 2013) at Yaw and Roll precision
and (Saragih et al., 2011) at Pitch and Roll precision.
The fully automatic method is marked (*) in Table
1; otherwise, it is the manual method. In addtion of
rigid tracking, our method is able to track non-rigid
parameters ((+) in Table 1). The other methods hav-
ing better results than us, is able to estimate only the
rigid parameter or is a manual method. Otherwise,
our method can estimate both rigid and non-rigid pa-
rameters, recover the lost-tracking while the training
data is synthetic.
The Talking Face Video: is a freely 5000-
frames video sequence of a talking face with available
ground-truth of 68 facial points on the whole video.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
42
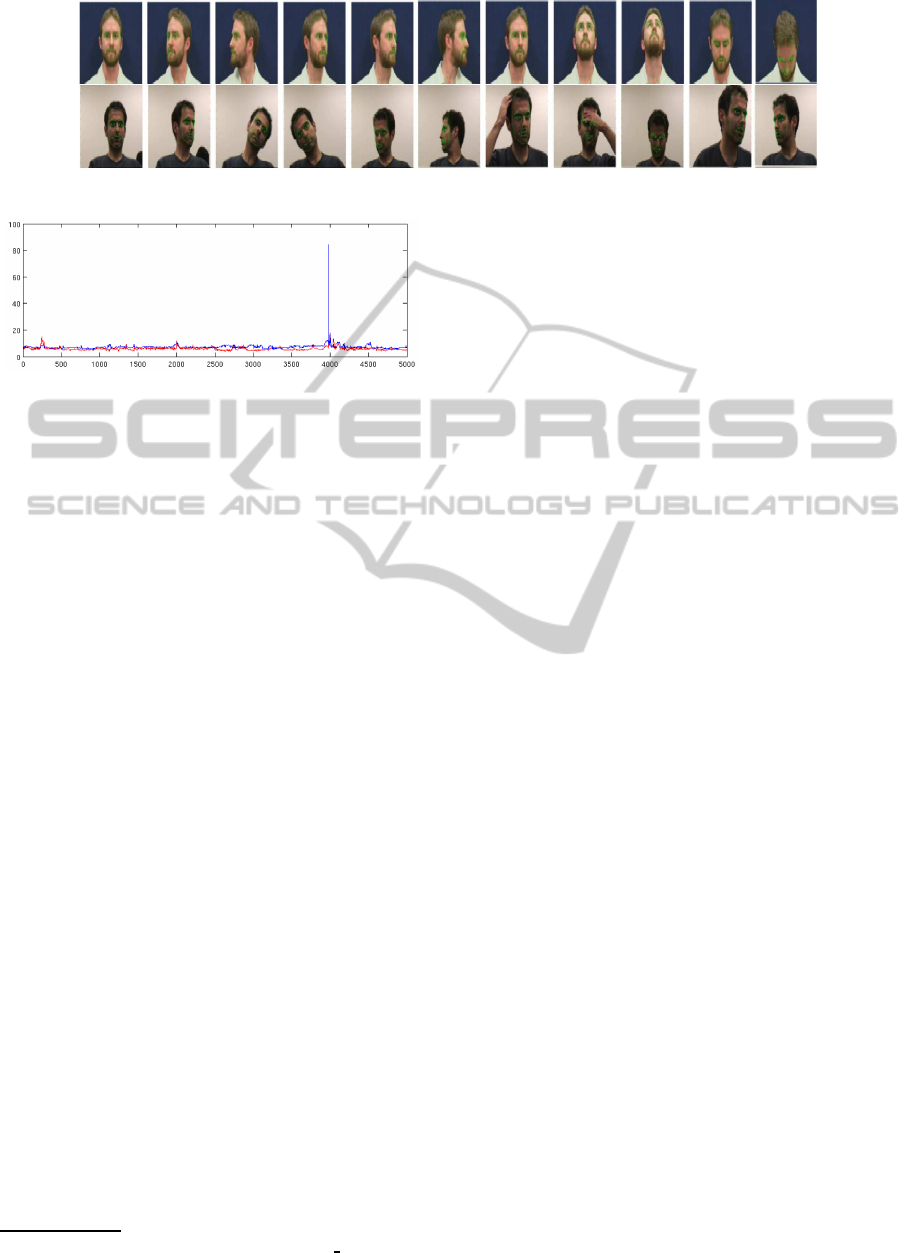
Figure 5: Our tracking method on some sample videos of VidTimid and Honda/UCSD.
Figure 4: The RMS of our framework (red curve) and Face-
Tracker (Saragih et al., 2011) (blue curve). The vertical axis
is RMS error (in pixel) and the horizontal axis is the frame
number.
The Root-Mean-Squared (RMS) error is used to mea-
sure the landmark tracking (non-rigid) precision. Al-
though the number of landmarks of methods is differ-
ent, the same evaluation scheme could be still applied
on the same number of selected landmarks. Twelve
landmarks at corners of eyes, nose and mouth are cho-
sen. The Fig. 4 shows the RMS of our method (red
curve), and FaceTracker (blue curve) (Saragih et al.,
2011) on the Talking Face video. The vertical axis
is the RMS error (in pixel) and the horizontal axis is
the frame number. The result shows that even though
our method just learned from the synthesized data,
what we obtain is comparable to the state-of-the-art
method, even more robust. The average precision of
the entire video of our method is 5.8 pixels and Face-
Tracker is 6.8 pixels.
VidTimid and Honda/UCSD: The VidTimid is
captured in resolution 512x384 pixels at the good of-
fice environment. Honda/UCSD dataset at resolution
640x480, is much more challenging than VidTimid
that provides a wide range of different poses at dif-
ferent conditions such as face partly occlusion, scale
changes, illumination, etc. The ground-truth of pose
or landmarks is unavailable in these databases; hence,
they are used for visualizing purpose of the profile
tracking. Our framework again demonstrates its capa-
bility even in more complex movements of the head.
In fact, our method is more robust than FaceTracker
in terms of keeping track unloosing and it can recover
face quickly without waiting for frontal face reset as
FaceTracker. See Fig. 5. Some full videos in paper
can be found at here
3
, in which one our own video
3
http://www.youtube.com/watch?v=yqAh1
2uaPA
is also recorded for evaluation. Our method is again
more robust on FaceTracker on this video.
Although real-time computation is unsustainable
(about 5s/frame on Desktop 3.1GHz, 8G RAM) due
to Matlab implementation. In which, the first step
is about 3s/frame because of SIFT matching. The
C/C++ implementation and the replacement of SIFT
by another faster descriptor is a possible future work.
In addition, our method is not robust with complex
background because no background is included in our
synthetic training data. The aware of background in
training process may be a possible solution.
5 CONCLUSIONS
We presented a robust framework for pose-free track-
ing of non-rigid face. Our method used the large
synthesized dataset rendering from a small set of
annotated frontal views. This dataset was divided
into groups to train pose-wise linear SVM classifiers.
The response map of one landmark is the combina-
tion of response maps from three descriptors: inten-
sity, gradient and LBP. Through keeping some can-
didates from one combined response map, we apply
an heuristic method to choose the best one via the
constraint of 3D shape model. In addition, the SIFT
matching makes our method robust to fast movements
and provides a good initial rigid parameters. Through
keyframes, our method can do recover the lost track-
ing quickly without waiting for frontal-view reset.
Our method is more robust than one state-of-the-art
method in terms of the profile tracking and compa-
rable in landmark tracking. However, our method is
still limited to work with complex background be-
cause of that no complex background is included in
training synthesized images. It can be more efficient
if the backgrounds of synthesized images are more
complex. In addition, the usage of SIFT matching is
slow and it needs to be improved for a real-time per-
formance as future direction.
TowardsPose-freeTrackingofNon-rigidFaceusingSyntheticData
43

REFERENCES
Aggarwal, G., Veeraraghavan, A., and Chellappa, R.
(2005). 3d facial pose tracking in uncalibrated videos.
In Proceedings of the First International Conference
on Pattern Recognition and Machine Intelligence.
Ahlberg, J. (2001). Candide-3 - an updated parameterised
face. Technical report, Dept. of Electrical Engineer-
ing, Linkoping University, Sweden.
Alonso, J., Davoine, F., and Charbit, M. (2007). A linear
estimation method for 3d pose and facial animation
tracking. In CVPR.
An, K. H. and Chung, M.-J. (2008). 3d head tracking and
pose-robust 2d texture map-based face recognition us-
ing a simple ellipsoid model. IROS, pages 307–312.
Asteriadis, S., Karpouzis, K., and Kollias, S. (2014). Vi-
sual focus of attention in non-calibrated environments
using gaze estimation. IJCV.
Besl, P. J. and McKay, N. D. (1992). A method for registra-
tion of 3-d shapes. TPAMI, 14(2):239–256.
Cao, X., Wei, Y., Wen, F., and Sun, J. (2012). Face align-
ment by explicit shape regression. In CVPR.
Cascia, M. L., Sclaroff, S., and Athitsos, V. (2000). Fast,
reliable head tracking under varying illumination: An
approach based on registration of texture-mapped 3d
models. TPAMI, 22(4):322–336.
Chen, Y. and Davoine, F. (2006). Simultaneous tracking of
rigid head motion and non-rigid facial animation by
analyzing local features statistically. In BMVC.
Cootes, T. F., Edwards, G. J., and Taylor, C. J. (2001). Ac-
tive appearance models. TPAMI, 23(6):681–685.
Cristinacce, D. and Cootes, T. F. (2006). Feature detection
and tracking with constrained local models. In BMVC.
Dementhon, D. F. and Davis, L. S. (1995). Model-based
object pose in 25 lines of code. IJCV, 15:123–141.
Dollar, P., Welinder, P., and Perona, P. (2010). Cascaded
pose regression. In CVPR.
FaceAPI. http://www.seeingmachines.com.
Fan, R.-E., Chang, K.-W., Hsieh, C.-J., Wang, X.-R., and
Lin, C.-J. (2008). LIBLINEAR: A library for large
linear classification. JMLR, 9:1871–1874.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: A paradigm for model fitting with appli-
cations to image analysis and automated cartography.
volume 24, pages 381–395.
Gross, R., Matthews, I., and Baker, S. (2006). Active ap-
pearance models with occlusion. IVC, 24(6):593–604.
Gross, R., Matthews, I., Cohn, J. F., Kanade, T., and Baker,
S. (2010). Multi-pie. IVC, 28(5):807–813.
Gu, L. and Kanade, T. (2006). 3d alignment of face in a
single image. In CVPR.
Jang, J.-S. and Kanade, T. (2008). Robust 3d head tracking
by online feature registration. In FG.
Koestinger, M., Wohlhart, P., Roth, P. M., and Bischof, H.
(2011). Annotated facial landmarks in the wild: A
large-scale, real-world database for facial landmark
localization. In First IEEE International Workshop on
Benchmarking Facial Image Analysis Technologies.
Lee, K., Ho, J., Yang, M., and Kriegman, D. (2003). Video-
based face recognition using probabilistic appearance
manifolds. volume 1, pages 313–320.
Lefevre, S. and Odobez, J.-M. (2009). Structure and ap-
pearance features for robust 3d facial actions tracking.
In ICME.
Lewis, J. P. (1995). Fast normalized cross-correlation. vol-
ume 1995, pages 120–123.
Matthews, I. and Baker, S. (2004). Active appearance mod-
els revisited. IJCV, 60(2):135 – 164.
Morency, L.-P., Whitehill, J., and Movellan, J. R. (2008).
Generalized adaptive view-based appearance model:
Integrated framework for monocular head pose esti-
mation. In FG.
Ojala, T., Pietik¨ainen, M., and Harwood, D. (1996). A com-
parative study of texture measures with classification
based on featured distributions. PR, 29(1):51–59.
Sanderson, C. (2002). The VidTIMIT Database. Technical
report, IDIAP.
Saragih, J. M., Lucey, S., and Cohn, J. F. (2011). De-
formable model fitting by regularized landmark mean-
shift. IJCV, 91:200–215.
Str¨om, J. (2002). Model-based real-time head tracking.
EURASIP, 2002(1):1039–1052.
Su, Y., Ai, H., and Lao, S. (2009). Multi-view face align-
ment using 3d shape model for view estimation. In
Proceedings of the Third International Conference on
Advances in Biometrics.
Tran, N.-T., eddine Ababsa, F., Charbit, M., Feldmar,
J., Petrovska-Delacrtaz, D., and Chollet, G. (2013).
3d face pose and animation tracking via eigen-
decomposition based bayesian approach. In ISVC.
Vacchetti, L., Lepetit, V., and Fua, P. (2004). Stable real-
time 3d tracking using online and offline information.
TPAMI, 26(10):1385–1391.
Wang, H., Davoine, F., Lepetit, V., Chaillou, C., and Pan,
C. (2012). 3-d head tracking via invariant keypoint
learning. IEEE Transactions on Circuits and Systems
for Video Technology, 22(8):1113–1126.
Wang, Y., Lucey, S., and Cohn, J. (2008). Enforcing con-
vexity for improved alignment with constrained local
models. In CVPR.
Xiao, J., Baker, S., Matthews, I., and Kanade, T. (2004).
Real-time combined 2d+3d active appearance models.
In CVPR, volume 2, pages 535 – 542.
Xiao, J., Moriyama, T., Kanade, T., and Cohn, J. (2003).
Robust full-motion recovery of head by dynamic tem-
plates and re-registration techniques. International
Journal of Imaging Systems and Technology, 13:85 –
94.
Xiong, X. and la Torre Frade, F. D. (2013). Supervised
descent method and its applications to face alignment.
In CVPR.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
44
