
A Mathematical Formulation for Estimating Age Levels
in the Carolina Curriculum
Salvatore Cuomo
1
, Antonella Olivo
3
, Pasquale De Michele
1
, Francesco Piccialli
1
,
Vincenzo Schiano Di Cola
1
and Ennio Del Giudice
2
1
Department of Mathematics and Applications “Renato Caccioppoli”,
University of Naples “Federico II”, Via Cintia 26, Naples, Italy
2
Department of Translational Medicine (Section of Pediatrics),
University of Naples “Federico II”, Via Pansini 5, Naples, Italy
3
Fondazione Istituto Antoniano di Ercolano, Via Madonnelle 15, Naples, Italy
Keywords:
Carolina Curriculum, Assessment Program, Support for Clinical Decision-making, Age Level Estimate.
Abstract:
The study of medical protocols for monitoring and analyzing the development of children with disabilities
is a fundamental research area. A well established curriculum-based assessment is the Carolina Curriculum
for Infants and Toddlers with Special Needs (CCITSN) together with the Carolina Curriculum for Preschool-
ers with Special Needs (CCPSN). These are suitable curriculums for early intervention programs, where se-
quenced item data collection and analysis are used to monitor incremental changes of the program and to
recognize the areas of relative strength and weakness in an individual infant, or child, with mild and moderate
disabilities. In many recent papers, Cuomo, et al. introduced the client-server software C@rolin@ to carry
out all features of CCITSN, afterwards a Social Framework and an App (CarolApp). Despite of all these tech-
nological advantages, the software uses mathematical formulas that do not fully satisfy operators and do not
help them to correctly establish useful parameters. We address this problem by developing a more formalized
mathematical model in the determination of age levels that can be successfully used in the Carolina software.
1 INTRODUCTION
The study of medical protocols for monitoring and
analyzing the development of children with disabil-
ities is a very spread out research area (cf. (Chap-
man and Hesketh, 2000)). Many studies in this
field are based on means-end behaviour, which in-
volves a painful execution of a sequence of steps to
achieve a goal. More in detail, this behaviour occurs
in situations where an obstacle preventing achieve-
ment of the goal must initially be removed (Piaget,
1953; Bruce et al., 2009). In this context, the Car-
olina Curriculum (CC) described in the books Car-
olina Curriculum for Infants and Toddlers with Spe-
cial Needs (CCITSN) (Johnson-Martin et al., 2004a)
and Carolina Curriculum for Preschoolers with Spe-
cial Needs (CCPSN) (Johnson-Martin et al., 2004b)
is a well established curriculum-based assessment for
young children with disabilities. The advantages of
the CC are intrinsically clear and well established. In
2006, in Italy, the CC has been adopted as a basic ser-
vice within several local Regional Service Systems
(ASL) (see (Del Giudice et al., 2006)). In (Cuomo
et al., 2011), a full web application software system,
named C@rolin@ and based on the CC protocol for
Infants and Toddlers, was presented. Unfortunately,
this software have presented weaknesses in the as-
signment of scores in the medical protocol. The aim
of this work is to develop a mathematical model for
the assignment of consistent scores. Moreover, we
have checked the idea on a phantom database of pa-
tients and our methodology is under revision of med-
ical staff. In a first feedback, doctors have assured us
that the scores are assigned in a consistent way. The
work is organized as follow: in Section 2 we recall
the history of the CC; in Section 3 we discuss the es-
timate of age level scores; in Section 4 we deal with
some application of the model; finally, the conclusion
are drawn in Section 5.
260
Cuomo S., Olivo A., De Michele P., Piccialli F., Schiano Di Cola V. and Del Giudice E..
A Mathematical Formulation for Estimating Age Levels in the Carolina Curriculum.
DOI: 10.5220/0005183502600267
In Proceedings of the International Conference on Health Informatics (HEALTHINF-2015), pages 260-267
ISBN: 978-989-758-068-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: The child curriculum panel.
Figure 2: The Data Report Panel.
2 PRELIMINARIES ON THE
CAROLINA CURRICULUM
In Figure 1 and Figure 2 we recall the main features of
the Carolina software system. This software allows,
from one side, to efficiently collect, represent, and
evaluate the relative data along the curriculum and,
from the other side, to support educators, doctors, vol-
unteers and therapists in the assessment-intervention
process of the children involved.
Moreover, the Carolina software allows all med-
ical operators involved in the process of the chil-
dren development skills to have a concurrent and real-
time access to all data, with respect to their own ac-
cess privileges and to add, modify, elaborate and or-
ganize them. Unfortunately the software presented
in (Cuomo et al., 2011) takes care only of the medical
aspects, which are basically recorded with a huge gap
of time intervals; to overcame the problem of the Car-
olina protocol, a Social Network Framework (Fig. 3)
for the Carolina software and consequently an App
(Fig. 4) has been developed and showed, respectively,
in (Cuomo et al., 2012) and (Cuomo et al., 2014).
Although the medical operator records patient as-
Figure 3: Web Based Social interaction module.
sessments at intervals of 6 months, families and chil-
dren can now communicate, ask questions and post
experiences on the software, thanks to the social net-
working service embedded in the Carolina software;
but the mathematical formulas implemented in order
to estimate age levels, still concerns many doctors.
This paper proposes a new framework for the mathe-
matical beyond the CC. Before presenting this model,
let us briefly examine what is the type of mathemat-
ical problem that need to be solved in the Carolina
Software.
After the recoding of the assessment, each opera-
tor wants to calculate:
• the development age,
• the development rate, and
• the partial performance index of the applied pro-
gram, for each domain and sequence.
This operation is performed by applying specific
formulas, each one developed in a specific module of
the software (cf. (Cuomo et al., 2011)).
Prior calculating the development age and rate; it
is calculated the weight (W ) of each item I, as follows
W =
TAP
NI
where TAP (Typical Attainment Period) is the typical
period during which a skill is acquired and NI is the
AMathematicalFormulationforEstimatingAgeLevelsintheCarolinaCurriculum
261
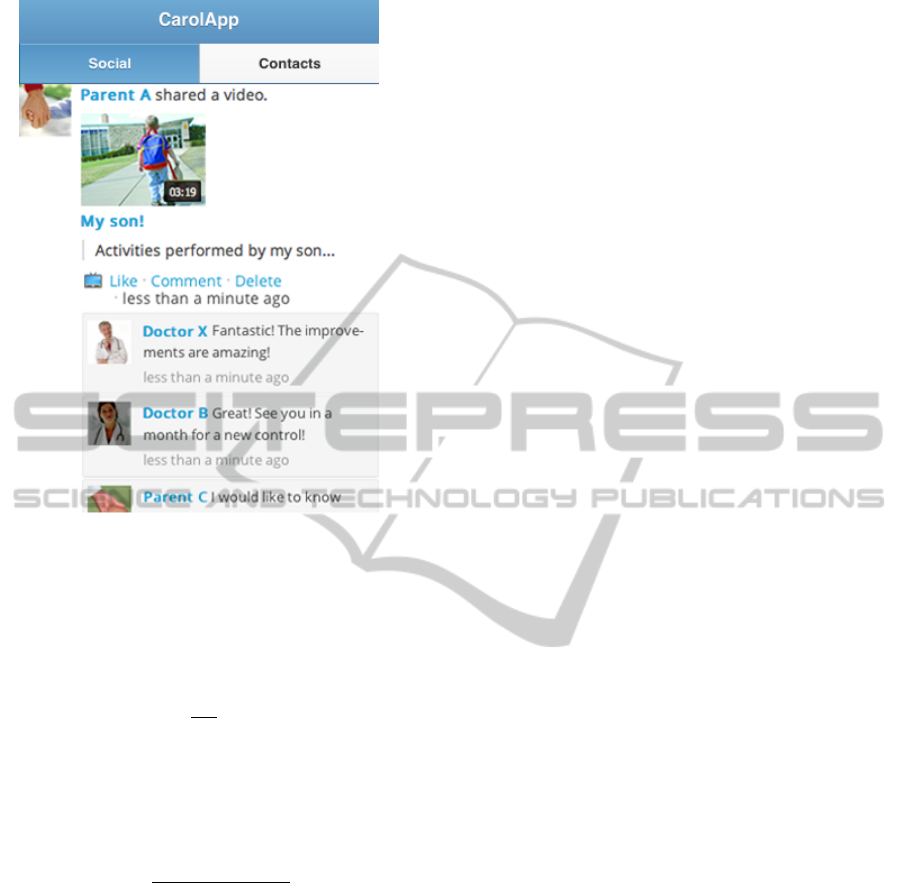
Figure 4: Carol App interaction: Sharing informations.
number of items (i.e. the Possible Points). Hence, the
development age is obtained by
DA = RS ·W (1)
where RS is the row score. The development rate is
DR =
DA
CA
· 100 (2)
where CA is the chronological age. Finally, the par-
tial performance index (IP) of the applied program
is equal to the performance between two subsequent
evaluations. Formally, it is expressed by the following
formula
IP =
DA(t
n
) − DA(t
n1
)
T
where T is the intervention time. Among these formu-
las, what mostly concerns doctors, is the fixed weight
formula that can bring to an inaccurate estimate of
the age level. In fact, doctors, have reported that the
estimated development age are meaningful when the
child evaluation is done at the beginning or at the end
of the age span of each group of items described in
the CC. Notice that each formula is based on the pre-
vious one, and great effort will be addressed in laying
the best foundation for these formulas, i.e. the calcu-
lation of age levels in the board domains.
In order to correctly develop a mathematical for-
mulation of the equations that will be used in the Car-
olina software, we will construct such formulation, by
taking into account all the possible information from
the Carolina Curriculum books (cf. (Johnson-Martin
et al., 2004a) and (Johnson-Martin et al., 2004b)). In
this Section we will present some useful extracts from
the books, and use this informations in order to define
the mathematical terms that will be used in Section 3,
when we will construct the new mathematical formu-
lation.
2.1 The Carolina Curriculum
Both the CCITSN and the CCPSN are divided into
24 logical teaching sequences covering 5 develop-
ment domains. These two books, starting from the
third edition of the CCITSN, are designed to provide
a guide for working with children who have special
needs from birth to 60 months. The sequence and the
item names of the infant and the toddler curriculum
are identical in both volume for the 24− to 36−month
range. Such continuum makes it possible for this ar-
ticle to address the mathematical formulation for the
entire CC, by making possible also an extension for
the software to the 60−months period.
Let us introduce the main terms used the CC. The
5 Development Domains are
1. Personal-Social,
2. Cognition,
3. Communication,
4. Fine-Motor,
5. Gross Motor.
Each domain is divided into sub-domains, called Cur-
riculum Sequences (or logical teaching sequence).
More specifically, a logical teaching sequence is a se-
quence of items and each item identifies a particular
skill that the child should acquire and express. Note
that three sequences:
1. Concepts/Vocabulary: Receptive,
2. Concepts/Vocabulary: Expressive,
3. Attention and Memory: Auditory,
are listed as Cognition-Communication. The skills as-
sessed in these sequences are included on almost all
tests of cognitive abilities and almost all tests of lan-
guage abilities. Thus, the three sequences belong to
the Cognition domain, as well as the Communication
domain; so they should be included in both when es-
timating a summary level of development for those
domains.
More in depth, a Curriculum Sequence is a se-
quence in which item order is primary determined by
how one skill builds in another, not only by the mean
age levels at which typical children learn the skill.
In fact, the items within each curriculum sequence
HEALTHINF2015-InternationalConferenceonHealthInformatics
262

are listed in the order of their expected development.
Each item lists criteria for determining when the child
has sufficiently mastered a skill and can move to more
advanced skill. Finally, in each curriculum sequence
items are grouped in age span, i.e. an interval time ex-
pressed in months that is a multiple of 3. So, each se-
quence is divided in to multiple items (so called in the
CC) that are age-dependent, i.e. each item describes
a skill that a child should acquire in a predetermined
month interval. Each item is a precise ability that the
child has to prove he knows how to do it.
2.2 Definitions
The CC does not assume that a child will develop at
the same rate across domains and the skills belong-
ing to a domain are unrelated to skills belonging to
other domains. We can study a generic domain, cal-
culate the age level in that domain, and then apply the
formulas to all the domains of the CC.
We will define the observation of a skill expressed
by each item as s
i
and each item can have value 0,
0.5 or 1 accordingly that the observers deduce that the
child does not have that skill, he quite has it, or he def-
initely has the skill. This is made in accordance with
the convention of the Assessment Log, which states
to tag each item with a plus (+) for skill the child has
mastered, a plus/minus (+/−) for an inconsistent or
emerging skill, and a minus (−) for a skill that the
child is unable to do. Observe that a child might have
or not the skill in a specific time, so, each s
i
must be a
function of time t, where the observer, in a particular
time, evaluates the skill, so that it will be s
i
(t) ∈ [0,1].
We also define a chronological age function, c(t),
of the child that is expressed in months (i.e. if the
child had 2 years 4 months and 15 day, then we write
24.5 months). The function c(t) is a function of time,
that has meaning from the date of birth, db, and will
be defined as
c(t) = t −db.
As for time t we also define an entering date t
0
in
which we establish the first time, among all the skills,
what the child has acquired or not. Then, there will be
an appropriate number of evaluation dates t
n
, where n
will vary across the total number of interventions that
will be necessary. Moreover at each evaluation date,
there will be an Item Rating in which the skills are
evaluated: s
i
(t
n
).
It is important to notice that the skills are age-
dependent, and some skill might be linked to ages
that are above the chronological age of the child. If
they were reported they would indicate some sort of
advanced performance of the child, and so an high de-
velopment rate (DR). To overcome these problems it
is important to define more precisely the s
i
, and their
use in the CC.
Parents, aid and professional, can be considered
as the observers of a phenomenon, which is the evo-
lution of a child that is acquiring new skills over time.
These observes can not assist this evolution second by
second, but at a certain time t
n
they observe the child
and deduce the level at which the child masters such
skill. So the only observables are: the skills s
i
and
the child chronological age c(t). The second is eas-
ily known, but the evaluation of the skills is not so
simple. In general, each skill can be considered as a
number that can vary from 0 to 1, and is a function
of the chronological age, and so a function of time.
Each function s
i
(c(t)) will indicate at a certain time
c(t) of the chronological age of the child how much
he is able to express that skill, moreover since the lin-
earity of c we will not always indicate such function
for the sake of briefness. So we will define a function
s
i
(t): [0,+∞) → [0,1].
Next, it is useful to associate at each observable
function s
i
(t), a standard function ¯s
i
(t), which will
indicate the typical period to obtain such skill. At
this standard functions (as well as to the observable
one) we will associate a month n
i
indicating when the
skill usually arises, and a month m
i
that indicates the
month, after which the skill is fully developed, and a
function f
i
(t) that indicates how the skill is obtained
in the period [n
i
,m
i
]. This function will be defined
¯s
i
(t) =
1, c(t) ≥ m
i
f
i
(c(t)), n
i
≤ c(t) ≤ m
i
0, c(t) ≤ n
i
.
These hypothesis are consistent with the concept of
age span in the CC.
Unfortunately the functions f
i
in ¯s
i
(t) are un-
known, and the CC books does not give enough de-
scriptions on how to correctly define such functions;
this is reasonable, since the CC is a curriculum-based
assessment.
It would be preferable to not fix any sort of hy-
pothesis on f
i
, but we will see that in order to evaluate
the skill of the child when his age does not coincide
with any of the n
i
or m
i
, we will have to specify f
i
,
and the simplest hypothesis that we can given is that
they are linear, i.e.
f
i
(t) =
c(t) − n
i
m
i
− n
i
.
The goal will now be to estimate the age of a child
with respect to a particular domain, i.e. DA(t) that
will express the development age of the child within a
AMathematicalFormulationforEstimatingAgeLevelsintheCarolinaCurriculum
263

domain. Notice that usually in children with problems
we observe
DA(t) < c(t).
3 AGE LEVEL ESTIMATE
Since we suppose that the domains are independent,
we will consider a generic domain D. The domain
will have a certain number of Curriculum Sequences
and each sequence will have a certain number of
skills.
We will describe the age estimate related to a
generic sequence S, and after it will we straightfor-
ward to apply it to our case, consisting of more than
one sequence in a domain. It is important to remem-
ber, that the age levels are estimates based on informa-
tion from standardized instruments and the literature
on infant and toddler development. It is not a score
based on standardized tests. It is also important to rec-
ognize that although standardized tests may provide
more accurate age levels (because they are based on
larger and more representative samples), these, too,
are estimates (cf. (Johnson-Martin et al., 2004a)).
The correctness of the proposed formulas will be
based on the application of the principles exposed in
the Carolina books that we have synthesized in Sec-
tion 2.1. In additions, many useful comments from
operators and doctors, helped us in these formulation.
3.1 Age Estimate in a Sequence
Let us consider a sequence S with NI items. Each se-
quence will mathematically be a set of functions de-
pending on time, i.e.
S =
{
s
i
(c(t)), i = 1, ... ,NI
}
,
and the s
i
are typically ordered such that n
i
≤ m
i+1
.
The skill described in s
1
is typically learned be-
fore s
2
, s
2
before s
3
, and so forth. Moreover, in each
curriculum sequence items are grouped in age span.
We also know, that ideally, if a child is observed
to have mastered s
3
of a sequence and not s
4
, it could
be assumed that the child has also mastered s
1
and
s
2
and will not have mastered s
5
and s
6
. A child of-
ten practices several related skills at once, however,
and there is little consistency as to which skill will
emerge first. Furthermore, specific impairments may
have different effects on the various skills within a se-
quence, disrupting the usual pattern of mastery. It is
important, therefore, that a sufficient number of items
be assessed in each sequence to be certain which skills
should be the focus of intervention. As a general rule,
the CC advises to continue administering items un-
til the child has passed all at one age span (e.g., 3–6
months) and has not met the criteria at another. In
this mathematical formulation, we can suppose that
in a certain age span, containing k items, skills that
go from s
i
to s
i+k
are all acquired in the time inter-
val n
i
−m
i+k
, where the months are known. We know
that the development of these skills in such age span
results in an overlap of those, but at the same time,
with the function s
i
, we have given the precise mean-
ing of what skill emerges, i.e. what can be observed.
By sticking with this definition, it is possible to sup-
pose that a skill s
i+1
is observed after s
i
, by giving
foundation to the hypothesis that the order in the set S
is given by the property: n
i
≤ m
i+1
.
Let us consider a child, whose age c(t) coincides
with a fixed month c(t) = m
k
= n
k−1
, and suppose
that min n
i
= 0. In this case, if we are interested in
the development age in a specific domain, as a first
approach, we can do a weighted average of all the
skills and multiply by the actual age, i.e.
DA(t) =
∑
i∈Θ(t)
s
i
(t)(m
i
− n
i
)
∑
i∈Θ(t)
(m
i
− n
i
)
· m
k
where the set Θ(t) is defined as
Θ(t) =
{
l : c(t) ≥ m
l
}
6=
/
0,
while we fix DA(t) = 0, if Θ(t) =
/
0.
This average, that uses the set Θ, does not con-
sider skills that are above the chronological age of
the child, and so preventing the reporting of an high
development quotient, and so solving one of the re-
ported problems noticed by medical operators in the
first versions of the software.
Now if we would like to evaluate a child whose
age is in between the typical interval of acquiring a
skill in a sequence, then we need to use the function
f
i
, and so
DA(t) =
∑
i∈Θ(t)∪θ(t)
s
i
(t)(m
i
− n
i
)
∑
i∈Θ(t)
(m
i
− n
i
) +
∑
i∈θ(t)
f
i
(t)(m
i
− n
i
)
· c(t)
(3)
where θ(t) =
{
l : n
l
≤ c(t) ≤ m
l
}
. If we suppose that
f
i
(t) is linear then (3) becomes
DA(t) =
∑
i∈Θ(t)∪θ(t)
s
i
(t)(m
i
− n
i
)
∑
i∈Θ(t)
(m
i
− n
i
) +
∑
i∈θ(t)
(c(t) − n
i
)
· c(t),
and we simply have the Development Rate
DR(t) =
DA(t)
c(t)
· 100%
HEALTHINF2015-InternationalConferenceonHealthInformatics
264

which is always less than 100%.
Now if we wish to consider a Sequence whose
minn
i
6= 0, then it is more convenient to start defin-
ing DR(t), by
DR(t) :=
∑
i∈Θ(t)
s
i
(t)(m
i
− n
i
) +
∑
i∈θ(t)
s
i
(t)(m
i
− n
i
)
∑
i∈Θ(t)
(m
i
− n
i
) +
∑
i∈θ(t)
(c(t) − n
i
)
or more in general we can define
DR(t) :=
∑
i∈Ω(t)
s
i
(t)(m
i
− n
i
)
∑
i∈Ω(t)
¯s
i
(t)(m
i
− n
i
)
where Ω(t) =
{
l : c(t) ≥ n
l
}
. Then, by introducing
N := min n
i
, we can define
DA(t) := N + DR(t) · (c(t) − N) .
This part settles the problem of determining the age
of the child in one generic sequence.
Let us compare the new formulation with the
method previously implemented in the Carolina Soft-
ware (cf. (Cuomo et al., 2011)). We rewrite the pro-
posed formula for the Development Age, (1),
DA = N +
∑
i
s
i
·
c(t) − N
NI
, (4)
in fact, this formula says that RS =
∑
i
s
i
(t
n
), and
TAP = c(t) − N. Since in general we have that
DA(t) = N +
∑
i∈Ω(t)
s
i
(t)(m
i
− n
i
)
∑
i∈Ω(t)
¯s
i
(t)(m
i
− n
i
)
· (c(t) − N) (5)
we can observe that the two equations (5) and (1) the
same if we consider two assumptions:
H1 the chronological age coincides with the maxi-
mum development age of the Sequence, i.e.
c(t
n
) = max
i=1,...,NI
m
i
;
H2 the intervals in which the skills are obtained
have all the same length, i.e.
m
i
− n
i
= L, ∀i = 1, ... ,NI.
In fact, under H1 and H2, we have
∑
i∈Ω(t
n
)
s
i
(t
n
)(m
i
− n
i
)
∑
i∈Ω(t
n
)
¯s
i
(t
n
)(m
i
− n
i
)
=
L ·
∑
i
s
i
L · NI
.
This proves that the new formulation proposed in this
paper is an extension of the previously used one, that
was meaningful under specific assumptions.
Let us end this section with some observations on
the proposed formulas of DR and DA, with respect of
the previous ones. In the new proposed model there
are two information that can not be deduced by the
CC books. The first one is the formulation of f
i
, the
second one is how to determine all the months n
i
, m
i
,
∀i = 1,...,NI. Both of these need further assump-
tions. In the first case we can suppose that the skill
of each item evolves linearly. In the second case, the
CC only states the age span, and the number of items
contained in each of them, and one simple approxi-
mation is to suppose the month interval in which such
skill usually arise are equally distributed. In this case,
if there are k + 1 skills in an age span, then the time
interval will be [n
i
,m
i+k
], where n
i
and m
i+k
are the
only given months from the CC books, and it is pos-
sible to fix
n
i+ j
=
j
m
i+k
− n
i
= m
i+ j−1
, ∀ j = 1, ...,k.
Notice that this formulation adheres to the hypothe-
sis that n
i
≤ m
i+1
. More advanced formulations, can
take into account overlapped skills, and appropriate
modifications on the function f
i
(t).
3.2 Age Estimate in a Domain
Since we can not tell that the Sequences within a par-
ticular Domain are independent of one another, we
should calculate the Development age not as a combi-
nation of the ages estimates in each Sequence age but
considering the items in every Sequence of a domain
all together. So let us introduce a Domain D with d
Sequences S
i
,
D =
d
[
i=1
S
i
,
and each Sequence will have NI
i
items, i.e.
S
i
=
s
i j
(c(t)), j = 1, ... ,NI
i
,
where we have added a second subscript to s(t), in
order to indicate to which Sequence it belongs.
From the previous section the Development Rate
for each Sequence S
i
is
DR
i
(t) :=
∑
j∈Ω(t)
s
i j
(t)(m
i j
− n
i j
)
∑
j∈Ω(t)
¯s
i j
(t)(m
i j
− n
i j
)
,
but if we want the same relation, in general among all
the skills of a Domain, we should define
DR(t) :=
∑
(i, j)∈Φ(t)
s
i j
(t)(m
i j
− n
i j
)
∑
(i, j)∈Φ(t)
¯s
i j
(t)(m
i j
− n
i j
)
where Φ(t) =
{
(k, l) : c(t) ≥ n
kl
}
. From this we sim-
ply have
DA(t) = DR(t) · c(t),
notice that there is no need to introduce N, since in
each domain of the CC, at least one Sequence starts
from n
1
= 0.
AMathematicalFormulationforEstimatingAgeLevelsintheCarolinaCurriculum
265
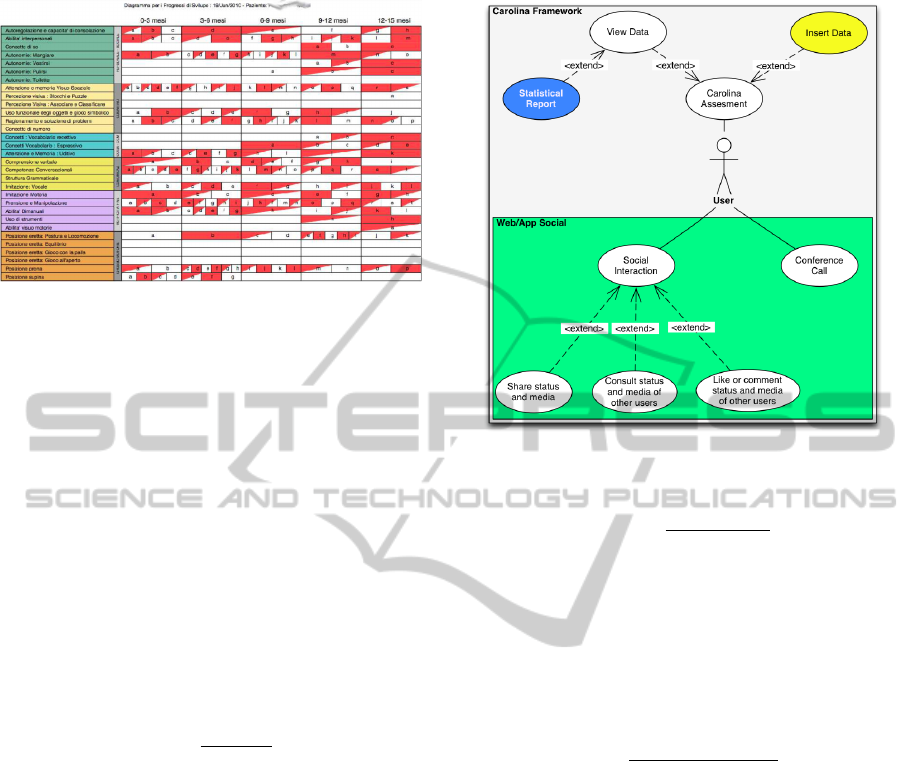
Figure 5: A Develop Progress Diagram (DPD). Blank cells
correspond to score 0 (−), red cells are equal to score 1 (+),
the remaining ones to score 0.5 (+/−).
4 MATHEMATICAL MODEL
APPLICATIONS
For the selection of the emerging skill, in order to cre-
ate a planner (Fig. 5) that draws the skills it is re-
quired the experience of the doctor. Here, we propose
useful tools to aid doctors in their selection.
Let us address how to select the emerging skill.
There is the calculation of the SS score, which is done
by DA − N. Then the doctor can observe the DR, cal-
culated as in (2), and finally ther is a Percentage De-
lay, calculated as
PD =
DA −CA
CA
and among all the Section of a Domain the median
values are calculated.
Then an emerging skill is selected in the Sections
that have a low Percentage Delay and also a low DR.
After the doctor proposes a target development rate
DR, which is higher than the calculated DR, and fi-
nally the doctor decides by whom the child must be
helped to improve such skill. In fact, the doctor dis-
cusses with the parents and the caregiver of the child,
about their goals in a long and short period, and even-
tually the doctor selects with the parents their next
goal.
Although in general such approach is meaningful,
it has the same flow as in the calculation of the devel-
opment rate. As the development rate becomes higher
than 100%, at the same time, the Percentage Delay is
bigger than 0%.
So, if we simply apply the proposed calculation of
the DR
i
(t) in some sequence S
i
, then we have a devel-
opment age DA
i
(t), and we can define the Percentage
Figure 6: Use case Diagram.
Delay
PD
i
(t) =
DA
i
(t) − c(t)
c(t)
.
Then the sections S
i
on which the doctors can focus
on are the ones whose PD
i
(t) is minimum. Most of
the used formulas should be correct, as long as one
appoints the proposed formalization of DA. There is,
for example, an Intervention Efficiency Index Sum-
mary Report. The partial performance index of the
applied program is defined as
IP =
DA(t
n
) − DA(t
n+1
)
T
where T is therapy time. This formula is consistent
as long as one uses the proposed formulation of the
Development Age.
All the proposed formulas are implementable in
the Application Tier of the Carolina software, and so
on its mobile version CarolApp. In a first implemen-
tation, such changes in the software are made only
in the business logic of the application, by having
direct improvements on the resulting age level esti-
mates, and can be viewed in the Data Report Panel
as in Figure 2. These changes are reflected in the
Use Case Diagram (Figure 6), from a software system
point of view, where we highlight the new features in-
troduced for the mathematical model. The improve-
ment is made in the Carolina web based features, by
modifying the Statistical Report module, that gener-
ates all the data that after are viewed by the doctor
through the View Data module.
In addition, new options can be added to the Client
Tier within the doctor’s related interface. This layer
HEALTHINF2015-InternationalConferenceonHealthInformatics
266

can be modified, in order to give more options to the
medical operators that can change the free parameters
in the estimate, accordingly to their personal experi-
ence and sensibility, to obtain a more accurate esti-
mate. These add-on could make the difference in case
of very sparse and scattered skills.
Finally, thanks to this mathematical framework
that improves the calculation of age estimate, it is pos-
sible to enhance the partial performance index. This
index indicates how well the child did in a time inter-
val, supposing that doctors have programmed the in-
tervention, and parents with operators have followed
such program. Thanks to this index, and a database
storing a vast amount of child cases, a machine learn-
ing algorithm can be applied to help doctors in im-
proving their intervention program, by opening a re-
search line to build up a system that can support them
during their decisions.
5 CONCLUSIONS
The Carolina is a software framework developed to
implement the Carolina Curriculum for Infants and
Toddlers with Special Needs. The software has
evolved over the years, moving from a client-server
application to a software system integrated with so-
cial network features.
In this work, we have developed a mathematical
model for the assignment of consistent scores. We
have overcome the main obstacle to give a cognitive
age value to the children that enter the curriculum in
different times of the medical protocol. This is a cru-
cial point because the entire program assessment is
a sequential medical procedure that goes on step by
step. The mathematical model is tested on a phan-
tom database of patients and is in advanced stages of
experimentation and doctors have assured us that the
scores are assigned in a consistent way. Future works
will be devoted to finish the test and the deploy of the
entire system and analyze more complete and inter-
esting experimental results about the real advantages
of the proposed mathematical model also considering
real data.
ACKNOWLEDGEMENTS
This paper is supported by the Associazione Italiana
per lo Studio delle Malformazioni (ASM) Onlus un-
der the grant:
Infrastrutture informatiche di supporto, monitoraggio
ed analisi di dati per bambini con malattie rare con-
genite e disabilit
`
a
REFERENCES
Bruce, S. M., Campbell, C., and Sullivan, M. (2009). Sup-
porting children with severe disabilities to achieve
means-end. TEACHING Exceptional Children Plus,
6:1–15.
Chapman, R. and Hesketh, L. (2000). Behavioral phenotype
of individuals with down syndrome. Mental Retar-
dation and Developmental Disabilities Research Re-
views, 6(2):84–95. cited By (since 1996)171.
Cuomo, S., De Michele, P., Piccialli, F., Del Giudice,
E., and Olivo, A. (2014). Carolapp: A mobile e-
health software project for remote monitoring of chil-
dren enrolled in the carolina curriculum. In Interna-
tional Conference on Health Informatics (HEALTH-
INF 2014).
Cuomo, S., Murano, A., and Piccialli, F. (2011). The
c@rolin@ software: A system for monitoring skills
development of children with down syndrome. pages
180–185. cited By (since 1996)2.
Cuomo, S., Murano, A., Piccialli, F., and Giudice, E. D.
(2012). A social network framework for the carolina
software. In Makedon, F., editor, PETRA, page 34.
ACM. cited By (since 1996)1.
Del Giudice, E., Titomanlio, L., Brogna, G., Bonaccorso,
A., Romano, A., Mansi, G., Paludetto, R., Di Mita,
O., Toscano, E., and Andria, G. (2006). Early inter-
vention for children with down syndrome in southern
italy: The role of parent-implemented developmental
training. Infants and Young Children, 19(1):50–58.
cited By (since 1996)4.
Johnson-Martin, N., Attermeier, S., and Hacker, B. (2004a).
The Carolina Curriculum for Infants and Toddlers
with Special Needs. P.H. Brookes Publishing Com-
pany.
Johnson-Martin, N., Hacker, B., and Attermeier, S. (2004b).
The Carolina Curriculum for Preschoolers with Spe-
cial Needs. P.H. Brookes Pub.
Piaget, J. (1953). The origin of intelligence in the child.
London: Routledge and Kegan Paul.
AMathematicalFormulationforEstimatingAgeLevelsintheCarolinaCurriculum
267
