
Plane Fitting and Depth Variance Based Upsampling for Noisy Depth
Map from 3D-ToF Cameras in Real-time
Kazuki Matsumoto, Francois de Sorbier and Hideo Saito
Graduate School of Science and Technology, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama, Kanagawa, Japan
Keywords:
Depth map, ToF depth sensor, GPU, Plane Fitting, Upsampling, denoising.
Abstract:
Recent advances of ToF depth sensor devices enables us to easily retrieve scene depth data with high frame
rates. However, the resolution of the depth map captured from these devices is much lower than that of color
images and the depth data suffers from the optical noise effects. In this paper, we propose an efficient algorithm
that upsamples depth map captured by ToF depth cameras and reduces noise. The upsampling is carried out
by applying plane based interpolation to the groups of points similar to planar structures and depth variance
based joint bilateral upsampling to curved or bumpy surface points. For dividing the depth map into piecewise
planar areas, we apply superpixel segmentation and graph component labeling. In order to distinguish planar
areas and curved areas, we evaluate the reliability of detected plane structures. Compared with other state-of-
the-art algorithms, our method is observed to produce an upsampled depth map that is smoothed and closer to
the ground truth depth map both visually and numerically. Since the algorithm is parallelizable, it can work in
real-time by utilizing highly parallel processing capabilities of modern commodity GPUs.
1 INTRODUCTION
In recent years, depth images have gained popularity
among many research fields including 3D reconstruc-
tion for dynamic scenes, augmented reality and en-
vironment perception in robotics. Depth images are
often obtained by stereo vision techniques, which are
computationally expensive and not able to calculate
the range data in non-texture scenes. This problem
was solved by the development of 3D time-of-flight
(3D-ToF) depth cameras, such as MESA Swissranger
and SoftKinetic DepthSense. A light source from the
camera emits a near-infrared wave to 3D objects and
the reflected light from scene objects is captured by
a dedicated sensor. By calculating the phase shift be-
tween the emitted light and the received one, the dis-
tance at each pixel can be estimated. Thus, ToF depth
cameras can acquire the range data even from texture-
less scenes in high frame rates.
However, the depth map captured by ToF depth
camera is unable to satisfy the requirements for de-
veloping rigorous 3D applications. This is due to the
fact that the resolution of the depth image is relatively
low (e.g. 160 × 120 pixels for SoftKinetic Depth-
Sense DS311) and the data is heavily contaminated
with structural noise. Moreover, the noise increases if
the infrared light interferes with other light sources or
is reflected irregularly by the objects.
In this paper, we propose joint upsampling and
denoising algorithm for depth data from ToF depth
cameras, which is based on local distribution of the
depth map. The upsampling is performed by simulta-
neously exploiting the depth variance based joint bi-
lateral upsampling and the plane fitting based on the
locally planar structures of the depth map. In order to
detect the planar area, we combine normal-adaptive
superpixel segmentation and graph component label-
ing. Our algorithm can discriminate between planar
surfaces and curved surfaces based on the reliability
of estimated local planar surface structure. Therefore
we can apply plane fitting to truly planar distributed
areas and utilize depth variance based joint bilateral
upsampling to curved or bumpy areas. As a result,
we can generate a smooth depth map while preserv-
ing curved surfaces. By using massively parallel com-
puting capabilities of modern commodity GPUs, the
method is able to maintain high frame rates. The re-
mainder of this paper is structured as follows. In Sec-
tion 2, we will discuss related works. After describing
the overview and the details of our technique in Sec-
tion 3. Section 4 will show the result of experiments
and discuss them. Finally we will conclude the paper
in Section 5.
150
Matsumoto K., de Sorbier F. and Saito H..
Plane Fitting and Depth Variance Based Upsampling for Noisy Depth Map from 3D-ToF Cameras in Real-time.
DOI: 10.5220/0005184801500157
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 150-157
ISBN: 978-989-758-077-2
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORKS
In order to upsample the depth data captured by a
ToF depth camera, several approaches have been pro-
posed which can be divided into two groups. The first
one deals with the instability of depth data provided
by the RGB-D camera by using several depth images
for reducing variations over each pixel depth value
(Camplani and Salgado, 2012) (Dolson et al., 2010).
However, these methods can not cope with numerous
movement of objects in captured scenes or require the
camera to be stationary.
The second group applies upsampling methods on
only one pair of depth and color images for inter-
polating depth data while reducing structural noise.
Among these methods, Joint Bilateral Upsampling
(Kopf et al., 2007) and the interpolation method
based on the optimization of a Markov Random Field
(Diebel and Thrun, 2005) are the most popular ap-
proaches. They exploit information from RGB im-
ages to improve the resolution of depth data under the
assumption that depth discontinuities are often related
to color changes in the corresponding regions in the
color image. However the depth data captured around
object boundaries is not reliable and heavily contam-
inated with noise.
(Chan et al., 2008) solved this problem by intro-
ducing a noise-aware bilateral filter, which blends the
results of standard upsampling and joint bilateral fil-
tering depending on the depth map’s regional struc-
ture. The drawback of this method is it can some-
times smooth the fine details of depth maps. (Park
et al., 2011) proposed a high quality depth map up-
sampling method. Since it extends nonlocal means
filtering with an additional edge weighting scheme, it
requires a lot of computational time.
(Matsuo and Aoki, 2013) presented a depth im-
age interpolation method by estimating tangent planes
based on superpixel segmentation. In this method,
depth interpolation is achieved within each region by
using Joint Bilateral Upsampling. (Soh et al., 2012)
also use superpixel segmentation for detecting piece-
wise planar surfaces. In order to upsample the low-
resolution depth data, they apply plane based interpo-
lation and Markov Random Field based optimization
to locally detected planar areas. These approaches can
adapt the processing according to local object shapes
based on the information form each segmented re-
gion.
Inspired from these approaches, we also use su-
perpixel segmentation for detecting locally planar
surfaces and exploit the structure of detected areas.
Compared with other superpixel based methods, our
method can relatively smooth depth map in real-time.
3 PROPOSED METHOD
Figure 1: Left: SoftKinetic DepthSense DS311. Center:
captured color image. Right: captured depth image.
As Figure 1 shows, we use SoftKinetic DepthSense
DS311 for our system, which can capture 640 × 480
color images and 160 × 120 depth maps at 25-60fps.
Before applying our method, we project each 3D
data from depth map onto its corresponding color im-
age by using rigid transformation obtained from cam-
era calibration between color camera and depth sen-
sor. In our experiment, we use the extrinsic parame-
ters given from a DepthSense DS311. After this pro-
cess, we can obtain RGB-D data in color image coor-
dinate frame.
However, it is still low resolution and includes
much noise and occluded depth data around the ob-
ject boundaries due to slight differences depth cam-
era and color camera positions. Therefore, we first
apply depth variance based joint bilateral upsampling
to the RGB-D data and generate highly smoothed and
interpolated depth map. Next, we calculate the nor-
mal map by applying the method proposed by (Holzer
et al., 2012). By using this normal map, we apply
normal-adaptivesuperpixel segmentation for dividing
the 3D depth map into clusters so that the 3D points in
each cluster make up a planar structure. For merging
clusters which are located on the same plane, graph
component labeling is utilized to segment image by
comparing the normals of each cluster. The plane
equation of each cluster is computed from the nor-
mal and center point associated with the cluster. After
that, we evaluate the reliability of each plane and dis-
criminate between planar cluster and curved cluster
and apply plane fitting and optimization to the depth
map. As a result, our method can generate smooth
depth maps which still contain complex shape infor-
mation.
3.1 Depth Variance Based Joint
Bilateral Upsampling
Joint Bilateral Upsampling(JBU) is a modification of
the bilateral filter, an edge-preserving smoothing filter
for intensity images. The smoothed depth value D
f
p
at the pixel p is computed from its neighboring pixels
PlaneFittingandDepthVarianceBasedUpsamplingforNoisyDepthMapfrom3D-ToFCamerasinReal-time
151

Ω as follows:
D
f
p
=
∑
q∈Ω
g
s
(p− q)g
c
(C
p
−C
q
)g
d
(D
p
− D
q
)D
q
∑
q∈Ω
g
s
(p− q)g
c
(C
p
−C
q
)g
d
(D
p
− D
q
)
(1)
where g
s
, g
c
, g
d
are Gaussian functions controlled by
the standard deviation parameters σ
s
Cσ
c
Cσ
d
respec-
tively. p − q represents the spatial distance, C
p
− C
q
is color similarity and D
p
− D
q
is the depth similarity.
As this equation shows, JBU locally shapes the spatial
smoothing kernel by multiplying it with a color simi-
larity term and a range term, and thus the edges can be
preserved while the non-edge regions are smoothed.
However, the depth map obtained from ToF depth
camera includes so much noise around the object
boundaries that JBU can suffer from the effects of the
noise. In order to remove the noise, we first calculate
the mean and standard deviation of specified depth
value around each pixel and if the variance is over the
threshold, the depth data is removed. After that, the
standard deviation is modified according to the depth
error’s quadratic dependance of distance defined by
(Anderson et al., 2005) as follows:
σ
′
l
=
cos(θ)σ
l
D
2
m
(2)
where σ
′
l
, D
m
and θ are the local standard deviation,
the local mean and the angle of incidence of infrared
light. Then, σ
c
is adapted to better reduce the noise
and preserve the edges as follows:
σ
c
= max{σ
c
0
+ λ· σ
′
l
,σ
min
} (3)
where σ
c
0
is a relatively high sigma of g
c
, σ
min
is the
minimum value, and λ is a negative factor. This mod-
ification is based on (Chen et al., 2012). Figure 2
shows the depth map captured in the scene of Figure
1 and the depth maps upsampled by JBU and depth
variance based JBU. Compared with the center image,
the noise around the object boundaries is removedand
the depth map is properly upsampled in right image.
After applying this technique, the smoothed and up-
sampled depth map is projected into 3D coordinates
using the intrinsic parameters of the color camera.
Figure 2: Left: input depth map. Center: JBU. Right: depth
variance based JBU.
3.2 Normal Estimation
After utilizing joint bilateral upsampling, the normal
estimation technique (Holzer et al., 2012) is applied
to the 3D points for computing a normal map in real-
time. This technique can generate a smooth normal
map by employing an adaptive window size to ana-
lyze local surfaces. As this approach also uses integral
images for reducing computational cost and can be
implemented in GPU, we can calculate normal maps
at over 50fps. However, this method can’t estimate
normals in the pixels around the object boundaries.
Therefore, we interpolate the normal map by calculat-
ing the outer product of two close points around these
invalid pixel vertices. The estimated normal map is
visualized in Figure 3.
3.3 Normal Adaptive Superpixel
Segmentation
(Weikersdorfer et al., 2012) proposed a novel over-
segmentation technique, Depth-adaptive superpixels
(DASP), for RGB-D images so that the 3D geom-
etry surface is partitioned into uniformly distributed
and equally sized planar patches. This clustering al-
gorithm assigns points to superpixels and improves
their centers using iterative k-means algorithms with
a distance computed from not only color distance and
spatial distance but also the depth value and normal
vector. By using the color image, the depth map cal-
culated in Section 3.1 and the normal map generated
in Section 3.2, we modify the DASP to use gSLIC
method by (Ren and Reid, 2011) in GPU.
The distance dist
k
(p
i
) between cluster k and a
point p
i
is calculated as follows:
dist
k
(p
i
) =
∑
j
w
j
dist
k
j
(p
i
)
∑
j
w
j
(4)
with the subscript j consecutively representing the
spatial(s), color(c), depth(d) and normal(n) terms. w
s
,
w
c
, w
d
and w
n
are empirically defined weights of
spatial, color, depth and normal distances, respec-
tively represented as dist
k
s
(p
i
), dist
k
c
(p
i
), dist
k
d
(p
i
)
and dist
k
n
(p
i
). Figure 3 illustrates the result of normal
adaptive superpixels, where the scene is segmented as
each region is homogeneous in terms of color, depth
and normal vector. The normal adaptive superpixel
segmentation gives for each cluster its C
k
(X
c
,Y
c
,Z
c
)
and its representative normal n
k
(a,b,c). As a result,
each point V
k
p
(X
k
p
,Y
k
p
,Z
k
p
) located on a locally pla-
nar surface of a cluster k can be represented as follows
aX
k
p
+ bY
k
p
+ cZ
k
p
= d
k
(5)
where d
k
is the distance between the plane and the ori-
gin. Assuming thatC
k
is located on the planar surface,
we can calculate d
k
as follows.
d
k
= aX
c
+ bY
c
+ cZ
c
(6)
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
152

Figure 3: RGB image: normal image: normal adaptive superpixels: merging superpixels.
3.4 Merging Superpixels
Since the superpixel segmentation is over-
segmentation proceduce, the post-processing is
required to find global planar structures. (Weikers-
dorfer et al., 2012) also provides the spectral grapth
theory, which extracts global shape information
from local pixel similarity. However, it requires
much computational time because it is not a parallel
procedure and can not be implemented in GPU.
Therefore, we apply graph component labeling with
GPUs and CUDA proposed by (Hawick et al., 2010)
to segmented images as illustrated in Algorithm 1.
By considering each representative planar equation
in given superpixel’s clusters, the labeling process is
carried out for merging clusters which are distributed
on the same planar area.
As Figure 3 shows, we can obtain the global pla-
nar area while preserving small planar patches in real-
time. Finally, the center and the representativenormal
vector of each region are computed again by taking
the average of normals and center points of the super-
pixels in each region.
3.5 Plane Fitting and Optimization
By using equation (5), 3D coordinates
V
k
p
(X
k
p
,Y
k
p
,Z
k
p
) on planar cluster k are com-
puted from normalized image coordinates u
n
(x
n
,y
n
)
as follows:
Z
k
p
=
d
k
ax
n
+ by
n
+ c
,X
k
p
= x
n
Z
k
p
,Y
k
p
= y
n
Z
k
p
(7)
By judging from the reliability of the plane model cal-
culated during the previous step, we can detect which
clusters are planar. The optimized point V
o
p
is gener-
ated by using V
f
p
computed from the depth variance
based JBU in section 3.1 and the variance of normal
vectors ψ
k
obtained in section 3.4 as follows:
V
o
p
=
V
f
p
(|V
f
p
−V
k
p
| > γ
V
2
k
p
cos(θ)
or ψ
k
> δ)
V
k
p
cosψ
k
+V
f
p
(1.0− cosψ
k
) (otherwise)
(8)
Algorithm 1: Superpixel Merging Algorithm.
function LabelEquivalenceHost(D,Size)
declare integer L[Size], R[Size]
do in parallel initialize L[0...Size − 1] and
R[0...Size−1] such that L[i] ← NASP[i] and R[i] ← i
declare boolean m
repeat
do in parallel in all pixels call
Scanning(D, L,R,m) and Labeling(D,L,R)
until m = false
return
function Scanning(D, L,R,m)
declare integer id,label
1
,label
2
,q
id
[9]
id ←pixel ithread ID)
label
1
,label
2
← L[id]
q
id
←neighbors of id
for all id
q
∈ q
id
do
declare float d
q
,θ
q
d
id
q
← |d
NASP[id]
− d
NASP[id
q
]
|
θ
id
q
← arccos(n
NASP[id]
× n
NASP[id
q
]
)
if d
id
q
< α and θ
id
q
< β then
min(label
2
,L[id
q
])
end if
end for
if label
2
< label
1
then
atomicMin(R[label
1
],label
2
)
m ← true
end if
return
function Labeling(D, L,R)
declare integer id,ref
id ←pixel (thread ID)
if L[id] = id then
ref ← R[id]
repeat
ref ← R[ref]
until ref = R[ref]
R[ref] ← ref
end if
L[id] ← R[L[id]]
return
PlaneFittingandDepthVarianceBasedUpsamplingforNoisyDepthMapfrom3D-ToFCamerasinReal-time
153

where θ is the incident angle of the infrared light from
a depth camera, γ and δ are the adaptively changing
thresholds specifically chosen for a given scene for
rejecting unreliable plane models. The huge error of
plane fitting will be removed by setting the threshold
γ. The threshold δ can prevent plane fitting from be-
ing applied to curved surfaces. Finally, we apply or-
dinary bilateral filter to V
o
p
for smoothing the artifacts
around boundaries.
4 EXPERIMENTS
We applied our method on two different scenes
captured by SoftKinetic DepthSense DS311(color:
640 × 480, depth: 160 × 120) and compared our re-
sult(PROPOSED) with other related works, Joint
Bilateral Filtering based Upsampling(JBF), Markov
Random Field(MRF), DISSS proposed by (Matsuo
and Aoki, 2013) and SPSR presented by (Soh et al.,
2012) in terms of runtime and qualitative evalua-
tion. For the quantitative evaluation, we gener-
ated the ground truth depth data with a scene ren-
dered via OpenGL. The ground truth depth data was
downsampled and added noise according to the noise
model of ToF depth camera described in (Anderson
et al., 2005). Then, we applied all methods to the
noisy depth data and calculated root-mean-square-
error(RMSE) and peak signal-to-noise ratio(PSNR)
between ground truth and the results in order to com-
pare the accuracy of all the methods. All processes
are implemented on a PC with Intel Core i7-4770K,
NVIDIA GeForce GTX 780, and 16.0GB of mem-
ory. We used OpenCV for trivial visualizations of
color and depth images as well as data manipulations,
and PointCloudLibrary for 3-dimensional visualiza-
tion. All GPGPU implementations were done using
CUDA version 5.0.
4.1 Qualitative Evaluation
Table 1 shows the parameters for each experiment.
We adjust the parameters for the superpixel segmen-
tation and merging superpixels so that we can divide
the depth map into truly planar areas. As Figure 6 and
7 demonstrate, our technique can generate smooth
and high resolution depth maps form low resolution
and noisy data captured by ToF depth camera. MRF
and JBF suffer from noisy data since these methods
estimate a pixel depth value from its neighborhood.
DISSS also applies joint bilateral upsampling in esti-
mated homogeneous surface regions and can’t repro-
duce smooth depth map. The upsampled depth map
from SPSR is smoothed because it uses both plane fit-
ting and markov random field to upsample the depth
data based on local planar surface equation estimated
by superpixel segmentation. However, as Figure 10
shows, fissures appear around the boundaries of each
region in the upsampled depth map because the su-
perpixel segmentation is processed locally. Figure 10
also shows that our method can obtain denoised depth
map particularly in areas of planar surfaces while pre-
serving the curved surfaces and the detail of objects
with complex shapes (e.g. the depth map of stanford
bunny). The reason is that our method can find global
planar areas and adapt the upsampling method based
on detected surface structures. Thanks to the prepro-
cessing explained in section 3.1, we can remove the
noise around the object boudaries as shown in Fig-
ure 9. In order to compare the runtime, all the meth-
ods are implemented with GPU and each runtime is
shown in Figure 4. Compared with other superpixel
based methods, our technique requires far less com-
putational time as shown in Figure 4.
Figure 4: Runtime (msec).
4.2 Quantitative Evaluation
Based on the characterization of the flash ladar de-
vices (Anderson et al., 2005), we presumed that the
depth value variance σ(p,d
gt
) at pixel p is discribed
as follows:
σ(p,d
gt
) = k
d
2
gt
cos(θ)
(9)
where d
gt
is the depth value acquired from ground
truth depth data, θ is the incident angle of the infrared
light from a depth camera and k is the noise coeffi-
cient. By using Box-Muller transform and equation
9, we added normally distributed random noise to the
downsampled ground truth depth based on the proba-
bility distribution described as follows:
p(d|d
gt
, p) ∝ exp
−
(d − d
gt
)
2
σ(p,d
gt
)
2
(10)
In order to evaluate the effectiveness of all meth-
ods, we applied them to noisy downsampled depth
data (640× 480,320× 240, 160× 120)and calculated
RMSE and PSNR. PSNR can be written as follows:
PSNR = 20log
10
d
max
RMSE
(11)
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
154

Table 1: Parameters for experiment.
Method Parameters Scene 1 Scene 2
Depth Variance Based JBU σ
s
, σ
c
, σ
d
, λ, σ
min
30, 50 , 100, −10, 15 70, 50 , 20, −10, 15
Superpixel Segmentation w
s
, w
c
, w
d
, w
n
50, 50 , 50, 150 50, 50 , 50, 150
iteration, clusters 1, 300 1, 300
Merging Superpixels@ α, β 220mm, π/8 75mm, π/12
Optimization@ γ, δ 0.0001, π/8 0.0001, π/8
Figure 5: RGB: normals: superpixels: merging superpixels.
Figure 6: Scene 1(a).
Figure 7: Scene 1(b).
Model 1 consists of three planar surfaces and Fig-
ure 11 shows the result of the experiment with Model
1. Our technique can generate the closest depth map
to the ground truth depth data because the method re-
places the noisy depth map entirely with a plane fitted
depth map. Model 2 is composed of planar surfaces
and curved surfaces. As Figure 13 illustrates, pro-
posed method is the most accurate method and SPSR
is the second of all the methods. Since SPSR applies
the plane fitting and MRF optimization to local pla-
nar patches, the noise reduction is performed locally
and that sometimes leads to fissure like discontinu-
ities around the edges of each region as we discussed
Figure 8: RGB: normals: superpixels: merging superpixels.
Figure 9: Scene 2(a).
Figure 10: Scene 2(b).
in 4.1. Moreover, the runtime of SPSR is the slowest
of all methods because of the edge refinement of su-
perpixel boundaries as shown in Table 4. Our method
is slower than JBF and MRF but it can still main-
tain high frame rates because of parallel processing
implemented in GPU. Our technique can reproduce
relatively accurate depth map compared with other
methods because it can distinguish planar regions and
curved regions and apply the appropriate algorithms
by combining planar fitting and depth variance based
joint bilateral upsampling. To conclude, our tech-
nique clearly outperforms other methods, in terms of
runtime, visual assessment and accuracy.
PlaneFittingandDepthVarianceBasedUpsamplingforNoisyDepthMapfrom3D-ToFCamerasinReal-time
155
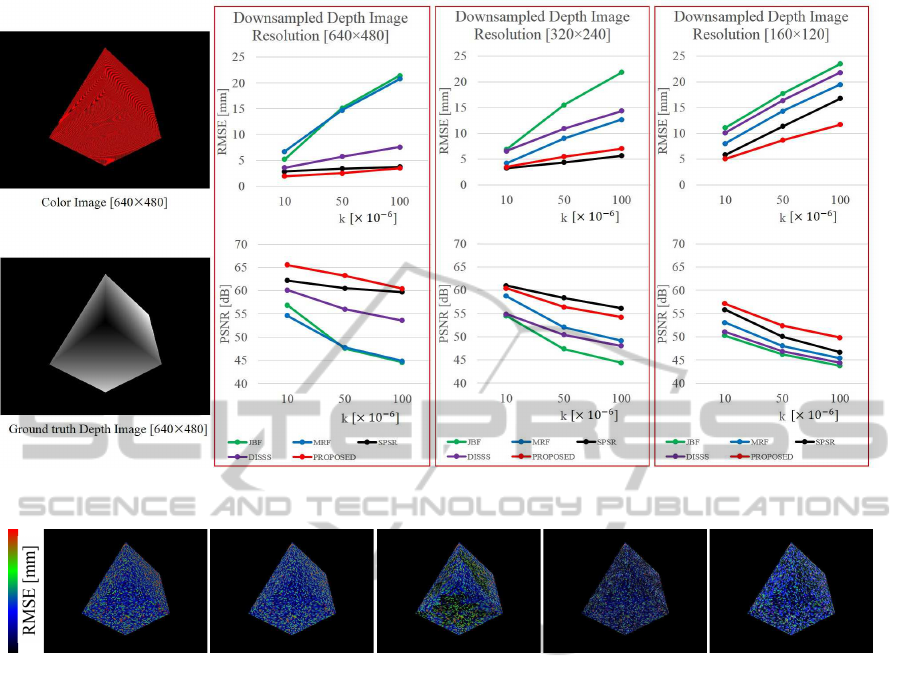
Figure 11: Model 1 RMSE and PSNR (d
max
= 3622.93mm).
0
50
JBF MRF
SPSR
DISSS
PROPOSED
Figure 12: Model 1 Visualization of RMSE (Input depth isize[160× 120], k=50×10
−6
).
5 CONCLUSIONS
In this work, we proposed a depth image upsampling
and denoising algorithm, which has a low resolution
depth image from ToF depth camera and a high reso-
lution color image as its inputs. In order to detect pla-
nar structures,we combined normal adaptive super-
pixels and graph component labeling by simultane-
ously using color image, depth data and normal map.
As our method can properly apply plane fitting and
depth variance based joint bilateral filter according to
the local points structure, it can generate smoothed
depth map retaining the shape of curved surfaces.
Our experimental results show that this technique
can upsample depth images more accurately than pre-
vious methods, particularly when applied to a scene
with large planar areas. Since the algorithm is paral-
lelizable, our framework can achieve real-time frame
rates thanks to GPGPU acceleration via CUDA archi-
tecture, which becomes crucial when such a method is
used in computationally expensive applications, such
as 3D reconstruction and SLAM.
ACKNOWLEDGEMENTS
This work is partially supported by National Insti-
tute of Information and Communications Technology
(NICT), Japan.
REFERENCES
Anderson, D., Herman, H., and Kelly, A. (2005). Experi-
mental characterization of commercial flash ladar de-
vices. In International Conference of Sensing and
Technology, volume 2.
Camplani, M. and Salgado, L. (2012). Adaptive spatio-
temporal filter for low-cost camera depth maps. In
Emerging Signal Processing Applications (ESPA),
2012 IEEE International Conference on, pages 33–36.
IEEE.
Chan, D., Buisman, H., Theobalt, C., Thrun, S., et al.
(2008). A noise-aware filter for real-time depth up-
sampling. In Workshop on Multi-camera and Multi-
modal Sensor Fusion Algorithms and Applications-
M2SFA2 2008.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
156
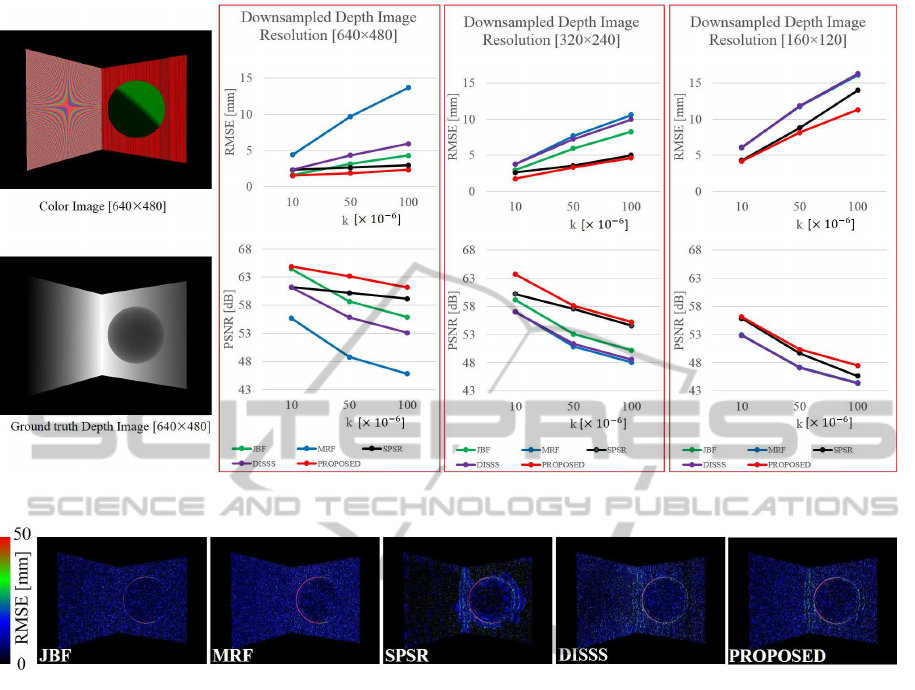
Figure 13: Model 2 RMSE and PSNR (d
max
= 2678.52mm).
Figure 14: Model 2 Visualization of RMSE (Input depth size [320× 240], k=50 ×10
−6
).
Chen, L., Lin, H., and Li, S. (2012). Depth image enhance-
ment for kinect using region growing and bilateral fil-
ter. In Pattern Recognition (ICPR), 2012 21st Inter-
national Conference on, pages 3070–3073. IEEE.
Diebel, J. and Thrun, S. (2005). An application of markov
random fields to range sensing. In Advances in neural
information processing systems, pages 291–298.
Dolson, J., Baek, J., Plagemann, C., and Thrun, S. (2010).
Upsampling range data in dynamic environments. In
Computer Vision and Pattern Recognition (CVPR),
2010 IEEE Conference on, pages 1141–1148. IEEE.
Hawick, K. A., Leist, A., and Playne, D. P. (2010). Par-
allel graph component labelling with gpus and cuda.
Parallel Computing, 36(12):655–678.
Holzer, S., Rusu, R. B., Dixon, M., Gedikli, S., and Navab,
N. (2012). Adaptive neighborhood selection for real-
time surface normal estimation from organized point
cloud data using integral images. In Intelligent Robots
and Systems (IROS), 2012 IEEE/RSJ International
Conference on, pages 2684–2689. IEEE.
Kopf, J., Cohen, M. F., Lischinski, D., and Uyttendaele, M.
(2007). Joint bilateral upsampling. In ACM Transac-
tions on Graphics (TOG), volume 26, page 96. ACM.
Matsuo, K. and Aoki, Y. (2013). Depth interpolation
via smooth surface segmentation using tangent planes
based on the superpixels of a color image. In Com-
puter Vision Workshops (ICCVW), 2013 IEEE Inter-
national Conference on, pages 29–36. IEEE.
Park, J., Kim, H., Tai, Y.-W., Brown, M. S., and Kweon, I.
(2011). High quality depth map upsampling for 3d-tof
cameras. In Computer Vision (ICCV), 2011 IEEE In-
ternational Conference on, pages 1623–1630. IEEE.
Ren, C. Y. and Reid, I. (2011). gslic: a real-time imple-
mentation of slic superpixel segmentation. University
of Oxford, Department of Engineering, Technical Re-
port.
Soh, Y., Sim, J.-Y., Kim, C.-S., and Lee, S.-U. (2012).
Superpixel-based depth image super-resolution. In
IS&T/SPIE Electronic Imaging, pages 82900D–
82900D. International Society for Optics and Photon-
ics.
Weikersdorfer, D., Gossow, D., and Beetz, M. (2012).
Depth-adaptive superpixels. In Pattern Recognition
(ICPR), 2012 21st International Conference on, pages
2087–2090. IEEE.
PlaneFittingandDepthVarianceBasedUpsamplingforNoisyDepthMapfrom3D-ToFCamerasinReal-time
157
