
Intuitionistic Fuzzy Sets with Shannon Relative Entropy
Lingling Zhao
1
, Yingjun Zhang
2
, Peijun Ma
1
, Xiaohong Su
1
and Chunmei Shi
3
1
School of Computer Science and Technology, Harbin Institute of Technology, Harbin, China
2
School of Computer and Information Technology, Beijing Jiaotong University, Beijing, China
3
Department of Mathematics, Harbin Institute of Technology, Harbin, China
Keywords: Pattern Recognition, Intuitionistic Fuzzy Sets (IFS), Distance Measure, Entropy.
Abstract: Bio-signal or bio-medical pattern recognition includes uncertainty. Intuitionistic fuzzy sets (IFSs) are
effective representation of the uncertainty factor. We present a pattern recognition method based on the
weighted distance of intuitionistic fuzzy sets (IFSs) in dealing with the fuzzy recognition problem. The
proposed method has a particular focus on handling the problem of choosing feature weights and feature
selection in the framework of IFSs. Depending on the idea of information-theoretic entropy and relative
entropy, a method is presented in dealing with the said two key problems, i.e., choosing feature weights and
feature selection. The proposed pattern recognition method in the framework of IFSs can not only represent
the dissimilarity between pair of features based on choosing feature weights but also reduce the
computational complexity depending on feature selection. Finally, a numerical example is utilized to
validate the proposed pattern recognition method.
1 INTRODUCTION
Zadeh (1965) and Yager (2000) emphasized the
importance of fuzzy set and its extended fuzzy sets
in the field of recognition technology. In many
domains such as finance, medicine, bio-medical,
defence, politics and marketing, a central problem is
object recognition under uncertainty (Larsen and
Yager, 2000). In the bio-medical diagnosis, many
problems include imprecise and imperfect facts.
How to model these problems with uncertainty and
hesitancy is still a challenge (Shinoj,2013) (Szmidt
and Kacprzyk, 2001) (Chung-ming, 2009).
Presently, fuzzy set and its extended fuzzy sets (such
as interval-valued fuzzy sets, intuitionistic fuzzy
set,L*-fuzzy set, intuitionistic[0,1]
−
fuzzy set, vague
set, grey set) have been tobe effective techniques in
dealing with above-mentioned classification
problems with uncertainty (Deschrijver and Kerre,
2007). Among them, intuitionistic fuzzy sets (IFSs),
proposed by Atanassov (1986; 1993), provide a
flexible mathematical way to cope with the
hesitancy originating from imperfect or imprecise
information. In an IFS, the membership degree and
non-membership degree are more or less
independent, and the only constraint is that the sum
of the two degrees must not exceed 1.
Various aspects of IFSs have been utilized for
decision making, pattern classification, and fuzzy
reasoning, where imperfect facts coexist with
uncertain knowledge (Li, 2010) (Hung and Yang,
2008) (Ciftcibasi and Altunay, 1998) (Cornelis,
Deschrijver and Kerre, 2004). In the context of
pattern recognition and classification, distance
measures, similarity measures, and correlation
measures of IFSs have been utilized aiming at the
pattern recognition problems under fuzzy
environment successfully (Hung and Yang, 2008)
(Liang and Shi, 2003) (Xu, 2007) (Wang and Xin,
2005) (Park et al., 2009). In the category of IFSs, the
weighted distance measure, proposed by Xu (2007),
takes into account the every element ’ s weight.
However, it is difficult to choose appropriate weight
of each element aiming at certain pattern recognition
problem under fuzzy environment. In this paper, we
shall present a framework for recognition
technology based on the weighted distance in the
category of IFSs, especially emphasized on the
choosing the feature weights and feature selection
depending on information entropy and its relative
theory(Hung and Yang, 2008)(Szmidt and Kacprzyk,
2001).
The remainder of this paper is organized as
follows: In Section 2 we introduce some preliminary
concepts. A distance measure of IFSs is introduced
150
Zhao L., Zhang Y., Ma P., Su X. and Shi C..
Intuitionistic Fuzzy Sets with Shannon Relative Entropy.
DOI: 10.5220/0005186001500157
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2015), pages 150-157
ISBN: 978-989-758-069-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

for pattern recognition problem using intuitionistic
fuzzy information particularly emphasized on the
choosing the weight of each feature and feature
selection in Section 3. In Section 4, we utilize some
pattern classification examples to validate the
pattern recognition model. Finally the article
concludes with a brief summary in Section 5.
2 PRELIMINARY
2.1 Review of IFSs
Since fuzzy set only gives a membership degree to
each element of the universe (Zadeh,1965),
Atanassov introduces the concept of IFS
characterized by a membership function and a non-
membership function, where non-membership is less
thanor equals to one minus the membership degree
(Atanassov, 1986). The concept of IFS is as follows:
Let Xbe a set. An IFS A in X is defined with the
form
,
,
| ∈
(1)
where
μ
:X→
0,1
,υ
:X→
0,1
(2)
are two maps satisfying
0μ
x
υ
x
1,forallx ∈ X. (3)
The numbers
and
denote the
membership degree and nonmembershipdegree of x
to A, respectively. For each IFS A in X, we call
π
x
1μ
x
υ
x
(4)
The intuitionistic index of x in A. If
= 0, the
IFS A reduces to a fuzzy set (Atanassov, 1986).
2.2 Relative Entropy
Relative entropy represents the amount of
discrimination between two probability distributions
(Shannon and Weaver, 1949).Let X be a discrete
random variable, and p(x) and q(x) be two
probability distributions for X. Kullback defined the
relative entropy between p(x) and q(x) as
D
p,q
∑
pxlog
∈
, (5)
where 0log
0 and log
∞
0.
Lin(1991), Hung and Yang(2008) pointed out
that p must be absolutely continuous with respect to
q, that is q(x)= 0 whenever p(x) =0. To overcome
this restriction, a modified cross-entropy measure
was introduces as (Hung and Yang, 2008) (Lin,
1991) (Vlachos and Sergiadis, 2007):
,
∑
log
∈
. (6)
Since
,
is not a symmetric measure, Hung
et al. introduced a symmetricmeasure H as follows:
,
,
,
. (7)
According to the above-mentioned
analysis,
,
is a symmetrical functionand
provides a measure to represent the divergence
between p and q.
3 PATTERN RECOGNITION
UNDER INTUITIONISTIC
FUZZY ENVIRONMENT
Distance measure is a term that represents the
difference between pair of IFSs. As an important
concept in the category of fuzzy sets, distance
measures of IFSs have also gained much attention
due to their extensive applications, such as decision
making, pattern recognition, clustering and market
prediction. So far, various calculation methods of
distance measures between IFSs have been proposed
in the latest decades. In the following part, we
introduce several classical distance measures. Let
,
,
| ∈
and
,
,
| ∈
be two IFSs in
,
,…,
. Bustince and Burillo(1995) proposed
the following two distance measures between A and
B. The Hamming distance and the Euclidean
distance are defined by Eq. (8) and (9). Szmidt and
Kacprzyk(2000) extended the work of Bustince and
,
∑|
|
|
|
(8)
,
∑
(9)
,
∑
|
|
|
|
|
|
(10)
,
∑
(11)
,
∑
|
|
|
|
|
|
(12)
IntuitionisticFuzzySetswithShannonRelativeEntropy
151
Burillo, the improved Hamming distance and
Euclidean distance are formulated by Eq. (10) and
(11), respectively. Basing on the above-mentioned
work, Xu (2007) introduced the distance measure by
Eq.(12) where 1, and
(i=1, 2,…,n) denotes
the weight of
(i=1, 2,…,n),which satisfies
0
and
∑
1
. According to the distance proposedby
Xu, (9) and (10) can be obtained from (11). More
distance measures ofIFSs were proposed in recent
years from different angles (see (Hung and Yang,
2008)(Xu, 2007) (Wang and Xin, 2005)(Szmidt and
Kacprzyk, 2000)(Guha and Chakraborty,
2010)(Zeng and Guo, 2008).
In general, the different features have different
importance in pattern recognition problem. Actually
a feature having great dissimilarity compared with
other features should be endowed with great weight
value (Seoung and Panaya, 2011). Therefore, it is
necessary to have a feature selection or choose
appropriate weights of features. Since the weighted
distance measures takes into account the weights’
divergence, it is helpful to describe the importance
of each feature. However, how to choose the weights
of features under intuitionistic fuzzy environment
belongs to a difficult problem which is the research
focus of this paper.
In the following part, we establish a pattern
recognition method based on the weighted distance
measure of IFSs, and particularly have an emphasis
on choosing the weight vector. Assume
,
,…,
and B be m+1 IFSs in the set
X=
,
,…,
, where
(1,2,…,), B, and
X denote the prototype, the unknown type and the
feature set (or attribute set), respectively.
According to the analysis in 2.2,
,
is
symmetrical function andcan be utilized to specify
the dissimilarity between the probability
distributionsp and q. For an IFS A in X, for all ∈,
we have
1,0
,
,
1 .This implies that
,
,
may be regarded as a
probability distribution. Therefore, we can utilize the
function H to consider the dissimilarity between
IFSs. Meanwhile, to represent the importance degree
of different attributes for the pattern recognition, the
weight vector is introduced and defined.
The weight
( 1,2,…,)is defined as
follows:
∙
∑
∙
,1,2,…, (13)
where 0and
∑∑
,
(14)
Obviously,
0. Since
is the sum of
symmetric measure, it can indicate the dissimilarity
degree of an attribute
. So
is suitable to
represent the weight of each attribute. Meanwhile
exponent expression ensures the weight always more
than zero. So the weight vector is an alterable
vector depending on choosing the differentvalues
of. We have the following proposition as follows:
Proposition 3.1.
1,2,…,
, if 0
or
for all ,∈1,2,…,.(2)
∗
1,
if
∗
max
,
,…,
∗
∈
1,2,…,
,
∗
for all
∗
∈
1,2,…,
, and lim ∞.
For revealing the variety of the weights resulting
from the different values of, in the following we
introduce an example.
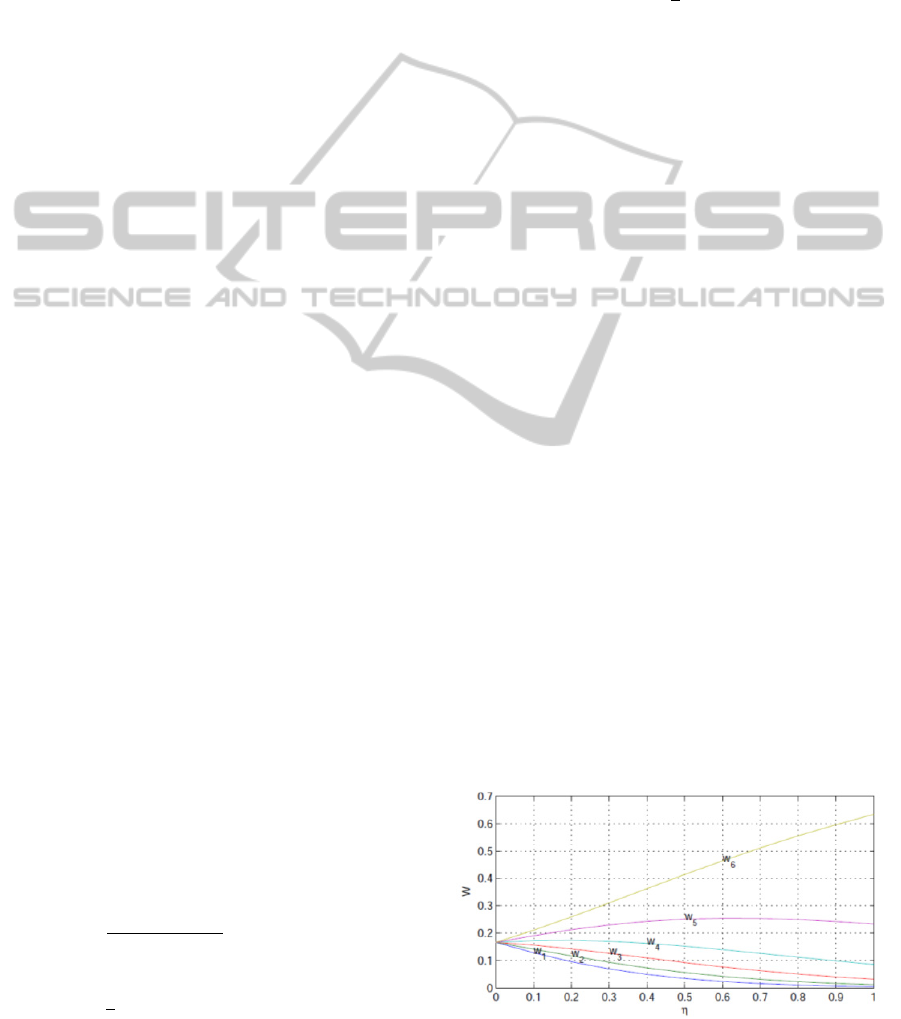
Example 3.1. The goal of this example is to
reveal the relationship between feature weight
and
in equation 13, so we can assume that the value of
( 1,2,3,4,5,6 ) is known, then we will
analyze the variety of
( 1,2,3,4,5,6) with the
different values of . Let
( 1,2,3,4,5,6) be
the following values: 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6,
0.7, 0.8, 0.9 and 1.0.
Now we setto be 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6,
0.7, 0.8, 0.9 and 1.0, respectively and compute the
corresponding
. Basing on (13), the weights of X
with different values of are listed in Table 1 and
shown in Figure 1. It implies that on the one hand
we can adjust the weights of features by choosing
different , on the other hand it is an effective way
to have a feature selection. In the following, we
construct the feature selection model and pattern
recognition model under intuitionistic fuzzy
environment.
Algorithm 1: Feature Selection
Let δ(0≤ δ<1) be a constant as the accepted
threshold of weights. The feature selection rule is
defined as follows:
a) Accept the feature
( 1,2,…,), if
δ
b) Reject the feature
(1,2,…,), if
.
Figure 1: The weights of X with different values of.
.
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
152

Remark: since δis the threshold of feature selection,
if
, it means attribute
is considered to be
useless for classification and will be ignored.
Thusδshould be a positive real number near zero, in
this paper we letδ=0.03. Also, there are some other
methods to decide the value of δ, for example,
δmean
/n , where n is the number of
attributes.
Basing on the rule of feature selection rule, we
construct the pattern recognition method under
intuitionistic fuzzy environment as below:
Algorithm 2: Pattern Recognition Based on
IFS with Shannon Relative Entropy
Step 1. Initializeandδ. is usually set to be 1
or 2.
Step 2. Compute
(1,2,…,) according to
(13) and (14), and havea feature selection.
Step 3. Compute the weights of the selective
features based on (13) and(14).
Step 4. Compute min{d(A,
)} (∈{1,2,…,m})
according to equation (12).
Step 5. If d(A,
) = min{ d(A,
)} (∈ {1, 2,…,
m}), then A belongs to
,
is a known pattern.
Remark: How to choose the parameter is a
difficult problem. Since is an adjusted parameter,
we suggest the parameter satisfying
,
,…,
,
,…,
10 . This strategy ensures a
majority of attributes to remain their contributions to
the classification and a minority of attributes to be
ignored.
4 NUMERICAL EXAMPLE AND
ANALYSIS
In this Section, we utilize two numerical examples in
the scenarios of the classification of building
material recognition and medical diagnosis to
validate the said pattern recognition method in the
framework of IFSs. Meanwhile we compare the
results obtained by the Hamming distance and the
Euclidean distance defined by Szmidt and Kacprzyk
(2001).
Example 4.1.There are four material prototypes
and an unknown type denoted by IFSs in
X=
,
,…,
in this pattern recognition problem
(Wang and Xing, 2005). The four prototypes and the
unknown type are represented as Table 2, where
( 1,2,3,4) and B denote the prototype and the
unknown type respectively.
Table 1: The weights of X with different values of..
0 0.1667 0.1667 0.1667 0.1667 0.1667 0.1667
0.1 0.1279 0.1414 0.1562 0.1727 0.1908 0.2109
0.2 0.0954 0.1166 0.1424 0.1739 0.2124 0.2594
0.3 0.0693 0.0935 0.1262 0.1704 0.2300 0.3105
0.4 0.0491 0.0732 0.1092 0.1629 0.2430 0.3626
0.5 0.0340 0.0560 0.0924 0.1523 0.2512 0.4141
0.6 0.0231 0.0421 0.0767 0.1397 0.2546 0.4639
0.7 0.0154 0.0311 0.0626 0.1260 0.2538 0.5111
0.8 0.0102 0.0226 0.0504 0.1121 0.2495 0.5552
0.9 0.0066 0.0163 0.0401 0.0985 0.2424 0.5961
1.0 0.0043 0.0116 0.0315 0.0858 0.2331 0.6337
Table 2: Data of the prototypes and the unknown type.
0.173 0.102 0.530 0.965 0.420 0.008 0.331 1.000 0.215 0.432 0.750 0.432
0.524 0.818 0.326 0.008 0.351 0.956 0.512 0.000 0.625 0.534 0.126 0.432
0.510 0.627 1.000 0.125 0.026 0.732 0.556 0.650 1.000 0.145 0.047 0.760
0.365 0.125 0.000 0.648 0.823 0.153 0.303 0.267 0.000 0.762 0.923 0.231
0.495 0.603 0.987 0.073 0.037 0.690 0.147 0.213 0.501 1.000 0.324 0.045
0.387 0.298 0.006 0.849 0.923 0.268 0.812 0.653 0.284 0.000 0.483 0.912
1.000 1.000 0.857 0.734 0.021 0.076 0.152 0.113 0.489 1.000 0.386 0.028
0.000 0.000 0.123 0.158 0.896 0.912 0.712 0.756 0.389 0.000 0.485 0.912
0.978 0.980 0.798 0.693 0.051 0.123 0.152 0.113 0.494 0.987 0.376 0.012
0.003 0.012 0.132 0.213 0.876 0.756 0.721 0.732 0.368 0.000 0.423 0.897
IntuitionisticFuzzySetswithShannonRelativeEntropy
153

Table 3: The weights with different.η.
Table 4: The weights of X with different values of ηafter feature selection.
Aiming at this pattern recognition problem, we
adopt two cases as follows:
4.1 Case 1
Assume that 1,2, and be with following
values: 0, 0.2, 0.4, 0.6, 0.8, 1.0,1.2, 1.4, 1.6, 1.8 and
2.0.
Step 1. According to the different values of ,
the weights of X are shownin Table 3.
Step 2.Let 1,2, compute the distance
d(
,) (i=1, 2, 3, 4) as Table 4.
Step 3. Since d(
,)=min d(
,),d(
,),
d(
,),d(
,) (=0, 0.2,…, 1.8, 2.0; =1, 2) for
every, B belongs to the prototype
.
Table 4 shows that d(
,) is a strictly
monotone decreasing function with the strictly
monotone increasing value of . The result of
distance measureswith different shows that the
proposed pattern recognition method can represent
the dissimilarity between pair of features.
Especially, when =0 and =1, 2, the weighted
distance measures reduce to the improved Hamming
distance measure and the improved Euclidean
distance, respectively (Szmidt and Kacprzyk, 2001).
4.2 Case 2
Assume that = 0.03, =1, 2, and be with
following values: 0, 0.2, 0.4,0.6, 0.8, 1.0, 1.2, 1.4,
1.6, 1.8 and 2.0. The pattern recognition process is
asfollows:
Step 1. The weights of X=
,
,…,
based
on the said values of are shown in Table 3.
Step 2. Let 0.03 , the weights of
X=
,
,…,
are shown in Table 5 after a
feature selection process.
Step 3. Compute the distance d(
,) (i=1, 2, 3,
4) based on the obtain weights in Step 2 with = 1,
2, and the results are shown in Table 6.
Step 4. Since d(
,)=min{d(
,),d(
,) ,
d(
,),d(
,)}(=0, 0.2,…, 1.8, 2.0; =1, 2) for
assumed parameters, B belongs to the prototype
.
When = 1.4, 1.6, 1.8, 2.0 and = 0.03, the
pattern recognition method firstly have a feature
selection. The pattern recognition results are the
same as the results without feature selection. From
the above-mentioned theoretical analysis and the
numerical results, it implies that the proposed
pattern recognition method provide an effective way
to have a feature selection and can reduce the
0 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833
0.2 0.0829 0.0878 0.0753 0.092 0.0759 0.0884 0.0728 0.0885 0.082 0.0916 0.0798 0.083
0.4 0.0819 0.092 0.0677 0.101 0.0688 0.0932 0.0633 0.0935 0.0803 0.1001 0.0759 0.0822
0.6 0.0806 0.0959 0.0605 0.1103 0.0621 0.0978 0.0547 0.0982 0.0782 0.1089 0.0719 0.0809
0.8 0.0789 0.0995 0.0539 0.1198 0.0557 0.1021 0.047 0.1026 0.0758 0.1178 0.0677 0.0793
1.0 0.0768 0.1027 0.0477 0.1295 0.0497 0.106 0.0402 0.1067 0.0731 0.1268 0.0635 0.0773
1.2 0.0744 0.1055 0.042 0.1394 0.0441 0.1096 0.0343 0.1105 0.0702 0.1359 0.0592 0.075
1.4 0.074 0.1111 0.0379 0.1538 0.0402 0.1162 0 0.1173 0.069 0.1493 0.0566 0.0746
1.6 0.0708 0.1126 0.033 0.1633 0.0352 0.1185 0 0.1198 0.0654 0.1578 0.0522 0.0715
1.8 0.0694 0.1171 0 0.1779 0.0317 0.1241 0 0.1255 0.0635 0.1712 0.0493 0.0702
2.0 0.0676 0.1208 0 0.1922 0 0.1288 0 0.1305 0.0612 0.1842 0.0462 0.0685
0 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833 0.0833
0.2 0.0829 0.0878 0.0753 0.0920 0.0759 0.0884 0.0728 0.0885 0.0820 0.0916 0.0798 0.0830
0.4 0.0819 0.0920 0.0677 0.1010 0.0688 0.0932 0.0633 0.0935 0.0803 0.1001 0.0759 0.0822
0.6 0.0806 0.0959 0.0605 0.1103 0.0621 0.0978 0.0547 0.0982 0.0782 0.1089 0.0719 0.0809
0.8 0.0789 0.0995 0.0539 0.1198 0.0557 0.1021 0.0470 0.1026 0.0758 0.1178 0.0677 0.0793
1.0 0.0768 0.1027 0.0477 0.1295 0.0497 0.1060 0.0402 0.1067 0.0731 0.1268 0.0635 0.0733
1.2 0.0744 0.1055 0.0420 0.1394 0.0441 0.1096 0.0343 0.1105 0.0702 0.1359 0.0592 0.0750
1.4 0.0718 0.1078 0.0368 0.1493 0.0390 0.1128 0.0291 0.1138 0.0670 0.1449 0.0550 0.0725
1.6 0.0690 0.1098 0.0322 0.1593 0.0344 0.1156 0.0245 0.1168 0.0638 0.1539 0.0509 0.0697
1.8 0.0661 0.1114 0.0280 0.1692 0.0302 0.1180 0.0206 0.1194 0.0605 0.1629 0.0469 0.0668
2.0 0.0630 0.1126 0.0243 0.1791 0.0264 0.1201 0.0173 0.1216 0.0571 0.1717 0.0430 0.0638
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
154

computational complexity.
The pattern recognition results of both Case 1
and Case 2 are the same as the results of (Hung and
Yang, 2008)(Xu, 2007) (Wang and Xin,
2005)(Vlachos and Sergiadis, 2007)(Szmidt and
Kacprzyk, 2000)(Guha and Chakraborty, 2010).
Example 4.2. In this example we utilize the data
set from literature (Szmidt and Kacprzyk, 2004) to
verify the performance of our method in the bio-
medical diagnosis application. Here there are four
patients: P={Al, Bob, Joe, Ted}. Disease
classification includes: D={viral Fever, Malaria,
Typhoid, Stomach problem, Chest problem}
The symptoms is defined by set S={temperature,
headache, stomach pain, cough, chest-pain}. The
relationship between patients and their symptoms,
symptoms and diseases are represented by IFSs as
table 7 and 8, respectively.
Table 5: Distances between
(i=1, 2, 3, 4) and B with different parameters.
η
λ=1 λ=2
d(A
,B) d(A
,B) d(A
,B) d(A
,B) d(A
,B) d(A
,B) d(A
,B) d(A
,B)
0 0.8744 0.8922 0.6434 0.4677 0.9192 0.9301 0.846 0.7901
0.2 0.8745 0.8935 0.6428 0.4603 0.9183 0.9278 0.8408 0.7826
0.4 0.874 0.8946 0.6421 0.4529 0.9171 0.9254 0.8357 0.7751
0.6 0.8731 0.8953 0.6415 0.4456 0.9156 0.9227 0.8306 0.7675
0.8 0.8715 0.8958 0.6407 0.4384 0.9137 0.9199 0.8257 0.7599
1 0.8695 0.8959 0.64 0.4313 0.9115 0.917 0.8207 0.7522
1.2 0.867 0.8957 0.6391 0.4244 0.9089 0.9138 0.8159 0.7445
1.4 0.8639 0.8952 0.6381 0.4175 0.906 0.9106 0.8111 0.7368
1.6 0.8605 0.8943 0.637 0.4108 0.9028 0.9072 0.8063 0.7291
1.8 0.8565 0.8932 0.6357 0.4042 0.8992 0.9036 0.8015 0.7214
2 0.8522 0.8918 0.6344 0.3978 0.8952 0.9 0.7968 0.7138
Table 6: Distances between
(i=1, 2, 3, 4) and B with different parameters.
=1 =2
d(
,) d(
,) d(
,) d(
,) d(
,) d(
,) d(
,) d(
,)
0 0.8744 0.8922 0.6434 0.4677 0.9192 0.9301 0.846 0.7901
0.2 0.8745 0.8935 0.6428 0.4603 0.9183 0.9278 0.8408 0.7826
0.4 0.874 0.8946 0.6421 0.4529 0.9171 0.9254 0.8357 0.7751
0.6 0.8731 0.8953 0.6415 0.4456 0.9156 0.9227 0.8306 0.7675
0.8 0.8715 0.8958 0.6407 0.4384 0.9137 0.9199 0.8257 0.7599
1 0.8695 0.8959 0.64 0.4313 0.9115 0.917 0.8207 0.7522
1.2 0.867 0.8957 0.6391 0.4244 0.9089 0.9138 0.8159 0.7445
1.4 0.8629 0.8883 0.6329 0.4084 0.9025 0.9046 0.8015 0.7269
1.6 1.7223 1.7768 1.2655 0.8114 1.2743 1.2776 1.1311 1.0235
1.8 2.5935 2.6815 1.9067 1.2151 1.565 1.5691 1.3882 1.2534
2 3.4475 3.584 2.5377 1.5982 1.8017 1.8075 1.5935 1.4333
Table 7: The IFSs of patients and their symptoms.
Temperature Headache Stomach pain Cough Chest pain
Al (0.8,0.1) (0.6,0.1) (0.2,0.8) (0.6,0.1) (0.1,0.6)
Bob (0.0,0.8) (0.4,0.4) (0.6,0.1) (0.1,0.7) (0.1,0.8)
Joe (0.8,0.1) (0.8,0.1) (0.0,0.6) (0.2,0.7) (0.0,0.5)
Ted (0.6,0.1) (0.5,0.4) (0.3,0.4) (0.7,0.2) (0.3,0.4)
Table 8: The IFSs of diseases and the symptoms.
R Viral fever Malaria Typhoid Stomach problem Chest problem
Temperature (0.4,0.0) (0.7,0.0) (0.3,0.3) (0.1,0.7) (0.1,0.8)
Headache (0.3,0.5) (0.2,0.6) (0.6,0.1) (0.2,0.4) (0.0,0.8)
Stomach pain (0.1,0.7) (0.0,0.9) (0.2,0.7) (0.8,0.0) (0.2,0.8)
Cough (0.4,0.3) (0.7,0.0) (0.2,0.6) (0.2,0.7) (0.2,0.8)
Chest pain (0.1,0.7) (0.1,0.8) (0.1,0.9) (0.2,0.7) (0.8,0.1)
IntuitionisticFuzzySetswithShannonRelativeEntropy
155

Table 9: The weights with different.η.
0 0.2 0.2 0.2 0.2 0.2
0.2 0.2173 0.1777 0.2188 0.1978 0.1882
0.4 0.2345 0.1570 0.2380 0.1944 0.1760
0.6 0.2516 0.1378 0.2571 0.1898 0.1635
0.8 0.2682 0.1202 0.2761 0.1843 0.1510
1 0.2842 0.1042 0.2948 0.1778 0.1387
1.2 0.2996 0.0899 0.3131 0.1706 0.1266
1.4 0.3141 0.07713 0.3307 0.1629 0.1150
1.6 0.3277 0.0658 0.3476 0.1547 0.1040
1.8 0.3404 0.0559 0.3636 0.1463 0.0936
2 0.3520 0.0474 0.3789 0.1378 0.0839
Table 10: Distances between the patients and diseases with.η1.
Viral fever Malaria Typhoid Stomach problem Chest problem
Al 0.3009
0.2159
0.3268 0.5857 0.5513
Bob 0.5034 0.6293 0.3835
0.1379
0.4493
Joe 0.3486 0.3934
0.3312
0.5660 0.5499
Ted
0.2566
0.2999 0.3339 0.4621 0.5025
Here we assume that λ2, and η be 1.0.
Step 1. According to the different values of η,
the weights of X are shownin Table 9.
Step 2. Let λ2, compute the distance d(P
,D
)
(i=1, 2, 3, 4,5 and j =1,2,3,4,5) as Table 10.
Step 3. Since d(P
,D
)=min d(P
,D
),d(P
,D
) ,
d(P
,D
),d(P
,D
) , d(P
,D
)) (η=1.0; λ=2), so the
patient P1, that is, Al suffers from malaria. Similarly,
Bob suffers from stomach problems, Joe from
typhoid and Ted from fever.
The diagnosis results are same with the method
proposed in (Szmidt and Kacprzyk, 2004), which
illustrates the effectiveness of our method.
Remark. The pattern recognition method based the
weighted distance measure of IFSs under
intuitionistic fuzzy environment not only provides a
calculation method for choosing weights of features
but also gives a method for feature selection.
5 CONCLUSIONS
In this paper, we construct the pattern recognition
method based on the weighted distance measures of
IFSs under fuzzy environment, especially emphasize
on feature selection and choosing feature weights.
This pattern recognition method provides a way to
choose the feature weights and to have a feature
selection depending on the information entropy
theory. The proposed pattern recognition method not
only provides a tool to represent the dissimilarity of
different features but also can reduce the
computational complexity through feature selection.
To illustrate that the pattern recognition method is
well suited in dealing with the fuzzy recognition
problems, we borrowed the data set from (Wang and
Xin, 2005). The results indicate that the proposed
pattern recognition method is good in representing
the feature weights and feature selection, and can
give the accurate pattern recognition results.
ACKNOWLEDGEMENTS
This research was supported by the National Natural
Science Foundation of China (NSFC) under Grant
61175027 and 61305013, the Fundamental Research
Funds for the Central Universities
(GrantNo.HIT.NSRIF.2014071), and Research Fund
for the Doctoral Program of Higher Education of
China(No.20132302120044).
REFERENCES
Zadeh L. A.,1965. Fuzzy sets, Information and Control, 8,
338-353.
Larsen H. L., 2000. Yager R. R., A Framework for Fuzzy
Recognition Technology, IEEE Transactions on
Systems, Man, and Cybernetics-Part C: Applications
and Reviews, 30, 65-70.
Shinoj T.K., Sunil J. J.,2013.Intuitionistic fuzzy multisets
and its application in medical diagnosis. World
Academy of Science, Engineering and Technology,6,
1414-1416.
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
156

Szmidt E., Kacprzyk J., 2001. Intuitionistic fuzzy sets in
intelligent data analysis for medical diagnosis.
International Conference on Computational Science,
263-271.
Chung-ming O.,2009. Switching between type-2 fuzzy
sets and intuitionistic fuzzy sets: an application in
medical diagnosis, Applied Intelligence, 31, 283-291.
Deschrijver G., Kerre E.E., 2007. On the position of
intuitionistic fuzzy set theory in the framework of
theories modelling imprecision, Information Sciences,
177, 1860-1866.
Atanassov K., 1986. Intuitionistic fuzzy sets, Fuzzy Sets
and Systems, 20, 87-96.
Atanassov K., Georgiev C., 1993. Intuitionistic fuzzy
prolog, Fuzzy Sets and Systems, 53, 121-128.
Li D. F., 2010. TOPSIS-Based nonlinear-programming
methodology for multiattribute decision making with
interval-valued Intuitionistic Fuzzy Sets, IEEE
Transactions on Fuzzy Systems, 18, 299-311.
Hung W. L., Yang M. S., 2008. On the J. divergence of
intuitionistic fuzzy sets with its application to pattern
recognition, Information Sciences, 178, 1641-1650.
Ciftcibasi T., Altunay D., 1998. Two-sided (intuitionistic)
fuzzy reasoning, IEEE Transactions on Systems, Man
and Cybernetics, Part A: Systems and Humans, 28,
662-677.
Cornelis C., Deschrijver G., Kerre E. E., 2004. Implication
in intuitionistic fuzzy and interval valued fuzzy set
theory: construction, classification, application,
International Journal of Approximate Reasoning, 35,
55-95.
Liang Z.Z., Shi P.F., 2003. Similarity measures on
intuitionistic fuzzy sets, Pattern Recognition Letters,
24, 2687-2693.
Xu Z. S., 2007. Some similarity measures of intuitionistic
fuzzy sets and their applications tomultiple attribute
decision making, Fuzzy Optimization and Decision
Making, 6, 109-121.
Wang W. Q., Xin X. L., 2005. Distance measure between
intuitionistic fuzzy sets, Pattern Recognition Letters,
26, 2063-2069.
Park D. G., Kwun Y. C., Park J. H., Park I. Y., 2009.
Correlation coefficient of interval-valued intuitionistic
fuzzy sets and its application to multiple attribute
group decision making problems, Mathematical and
Computer Modelling, 50, 1279-1293.
Szmidt E., Kacprzyk J., 2001. Entropy for intuitionistic
fuzzy sets, Fuzzy Sets and Systems, 118, 467-477.
Shannon C.E.,Weaver W., 1949.The mathematical theory
of communication, 3-91. University of Illinois Press,
Urbana.
Lin, J., Divergence measures based on the Shannon
entropy, IEEE Transaction on Information Theory, 37,
145-151, (1991).
Vlachos I. K., Sergiadis G. D., 2007.Intuitionistic fuzzy
information-Applications to pattern recognition,
Pattern Recognition Letters, 28, 197-206.
Bustince H., Burillo P., 1995. Correlation of interval-
valued intuitionistic fuzzy sets, Fuzzy Sets and
Systems, 74, 237-244.
Szmidt E., Kacprzyk J.,2000. Distances between
intuitionistic fuzzy sets, Fuzzy Sets and Systems, 114,
505-518.
Guha D., Chakraborty D., 2010.A new approach to fuzzy
distance measure and similarity measure between two
generalized fuzzy numbers, Applied Soft Computing,
10, 90-99.
Zeng W. Y., Guo P., 2008. Normalized distance, similarity
measure, inclusion measure and entropy of interval-
valued fuzzy sets and their relationship, Information
Sciences, 178, 1334-1342.
Seoung B. K., Panaya R., 2011. Unsupervised feature
selection using weighted principal components. Expert
Systems with Applications, 38, 5704-5710.
Szmidt, E., Kacprzyk, J., 2004. A similarity measure for
intuitionistic fuzzy sets and its application in
supporting medical diagnostic reasoning. Artificial
Intelligence and Soft Computing-ICAISC 2004,
Springer Berlin Heidelberg, 388-393.
IntuitionisticFuzzySetswithShannonRelativeEntropy
157
