
Sparse-input Detection Algorithm with Applications in
Electrocardiography and Ballistocardiography
F. Wadehn
∗,1
, L. Bruderer
∗,1
, D. Waltisberg
2
, T. Keresztfalvi
1
and H.-A. Loeliger
1
1
Signal and Information Processing Laboratory, ETH Zurich, Gloriastrasse 35, Zurich, Switzerland
2
Institut fuer Elektronik, ETH Zurich, Gloriastrasse 35, Zurich, Switzerland
Keywords:
Ballistocardiography, Heart Rate Estimation, Hypothesis Test, Factor Graphs, System identification, State-
space Models, Maximum likelihood, Maximum a posteriori.
Abstract:
Sparse-input learning, especially of inputs with some form of periodicity, is of major importance in bio-
signal processing, including electrocardiography and ballistocardiography. Ballistocardiography (BCG), the
measurement of forces on the body, exerted by heart contraction and subsequent blood ejection, allows non-
invasive and non-obstructive monitoring of several key biomarkers such as the respiration rate, the heart rate
and the cardiac output. In the following we present an efficient online multi-channel algorithm for estimating
single heart beat positions and their approximate strength using a statistical hypothesis test. The algorithm
was validated with 10 minutes long ballistocardiographic recordings of 12 healthy subjects, comparing it to
synchronized surface ECG measurements. The achieved mean error rate for the heart beat detection excluding
movement artifacts was 4.7%.
1 INTRODUCTION
Cardiovascular diseases are among the leading causes
of death and severe health impairments both in high-
income countries with an aging population, as well
as in developing countries, which are increasingly
adopting western sedentary lifestyles and diet (Yusuf
et al., 2001). Cardiac monitoring appliances range
from high resolution devices such as multi-lead
ECG or the invasive esophageal ECG (Schnittger
et al., 1986) to non-invasive, non-obstructive long
time monitoring systems among which pulse oxime-
try (Yelderman and New Jr, 1983) and ballistocardio-
graphy (BCG) (Alihanka et al., 1981) are the most
prominent. In ballistocardiography, forces exerted by
ventricular blood ejection are measured with force
sensors, usually placed below or inside a mattress on
which patients are lying. These force measurements
can be used to infer heart rates, heart rate variability
and even for getting indications about the cardiac out-
put (Cathcart et al., 1953; Inan et al., 2009). BCG sig-
nals can be interpreted as an overlap of several oscilla-
tions of the body-bed-sensors system. Figure 1 shows
a filtered (see Section 3.1) single channel BCG signal
and heart-beat times (time of R peak in QRS com-
plex), extracted from a synchronized surface ECG.
∗
These two authors contributed equally
Early signal-processing methods for BCG signals
(Watanabe et al., 2005; Mack et al., 2009) concerned
estimation of heart rates averaged over a few sec-
onds using frequency-based methods. These meth-
ods do not provide beat-to-beat resolution or infor-
mation on irregular arrhythmias. Recently, advanced
applications such as heart rate variability analysis or
sleep staging, have brought up the challenging task
of detecting individual heart beats in a BCG signal.
Schemes that rely on a single peak of a, possibly
preprocessed, BCG signal lack robustness for most
applications due to oscillations caused by one heart
beat that decay slowly and overlap with the next heart
beat (Bruser et al., 2011).
A variety of methods, proposed for beat-to-beat
detection are based on, possibly adaptive, template
matching techniques (Shin et al., 2008; Paalasmaa
et al., 2014) or sets of features extracted from the
BCG signal (Friedrich et al., 2010; Bruser et al.,
2011). These approaches have in common that they
are not based on a probabilistic framework and their
performance, which relies on specific patterns of
troughs and peaks, might decrease, if used with stiff
systems, where oscillations have not sufficiently de-
cayed and the following impulse might lead to de-
structive interference. In addition, these algorithms
were developed for single-channel measurement sce-
21
Wadehn F., Bruderer L., Waltisberg D., Keresztfalvi T. and -A. Loeliger H..
Sparse-input Detection Algorithm with Applications in Electrocardiography and Ballistocardiography.
DOI: 10.5220/0005186600210030
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2015), pages 21-30
ISBN: 978-989-758-069-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
0
0.5
1
1.5
2
Time [s]
BCG a.u.
Figure 1: Filtered single channel BCG signal (solid) with
heart beat positions (red).
narios. Extension of these schemes to process multi-
channel measurements, thus taking advantage of more
information, is not readily possible. In addition the
aforementioned algorithms are tailored to extract in-
stantaneous heart rates from the BCG signals, but do
not recover estimates of the relative strength of heart
beats.
In this paper, we present a robust heart-beat detec-
tion algorithm, which can be used to extract beat-to-
beat estimates (e.g., heart rate or the heart rate vari-
ability) from ballistocardiogram measurements. By
means of an initial training step the method adapts
itself to the present BCG data. Individual heart-
beat then detects beats in a recursive window-based
fashion, using a probabilistic model of the BCG sig-
nal. Core of the model is a state-space model rep-
resentation of the BCG signal and an computation-
ally efficient method for performing hypothesis test-
ing (Reller, 2012). Owing to the explicit modeling of
the BCG heart beat pulses our method is thus robust
when dealing with beat-to-beat interference in the
measurements. Furthermore, the probabilistic treat-
ment allows to quantify the reliability of a poten-
tial heart beat detection and is leveraged for removal
of small artifacts in the signal. Lastly, the estima-
tion algorithm being based on a maximum likelihood
hypothesis-testing procedure, apart from estimates of
heart-beat time also infers the relative magnitude of
beats. Information on the heart beat’s relative magni-
tude might be useful to get indications on the cardiac
output (Kurumaddali et al., 2014).
The paper is structured as follows. At first the
BCG signal’s is presented along with our algorithm to
detect individual heart beats and estimate their magni-
tude (Section 2). The employed validation dataset and
necessary pre-processing are then discussed (Section
3), followed by the results (Section 4).
7.6
7.8 8 8.2 8.4
Time [s]
Amplitude a.u.
BCG
4-th order
8-th order
14-th order
Figure 2: One hearbeat period segment of a measured BCG
signal and the estimated state-space model’s outputs, ob-
tained with the presented bootstrap system identification
approach. Subspace identification with 4-th, 8-th, and 14-
th order model resulted in normalized root-mean-squared-
error (NRMSE) fits
1
of 32%, 44%, and 52% respectively
evaluted on the training data.
2 ALGORITHM DESCRIPTION
We model BCG signals as a time-shifted sum of beats.
Each beat in turn is modeled as a linear combina-
tion of exponentially-decaying oscillations with addi-
tive white Gaussian noise. Using linear discrete-time
state-space models these signals are described as fol-
lows
X
k
= AX
k−1
+ BU
k
Y
k
= CX
k
+ Z
k
,
(1)
where the input signal U
k
represents the heart beat
train, Y
k
models the measured BCG signal, and Z
k
∼
N (0,V ) is the observation noise. The heart beat train
is modeled as a scaled non-uniformly spaced Kro-
necker comb
U
k
=
N
∑
n=0
δ[k − T
n
] · α
n
, T
n
∈ N, (2)
with N heart beats and scaling factors α
n
, which serve
as indication for the instantaneous cardiac output.
The heart-beat times T
n
and the scaling factors α
n
are
unknown and estimated from the BCG signal.
The proposed method used to infer the temporal
pattern of heart-beats, consists of a model-estimation
step, followed by a robust beat-detection algorithm.
The purpose of the model-estimation step is to iden-
tify a suitable state-space model representation in
1
NRMS is computed as follows
1 −
k
~
Y −
ˆ
~
Y k
k
~
Y − 1/K
∑
K
k=1
Y
k
k
!
100%,
where Y and
ˆ
Y represent the stacked BCG measurements
and predictions of the estimated model.
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
22

Algorithm 1: Sparse-input detection.
1: Pre-processing (Section 3.1)
2: 6σ artifact labeling (Section 2.4)
3: Bootstrapped state-space model identification
4: Robust heart-beat detection (Sections 2.2-2.4)
5: Outlier rejection (Section 2.5)
(1) of the current BCG signal. To this end, sub-
space methods were selected, due to their efficiency
and their numerical stability (Van Overschee and
De Moor, 1996). Subspace methods (e.g., 4SID) are
based on the idea that an estimate of the state se-
quence ˆx can be directly estimated from input/output
data. Once the state-space sequence is estimated, the
system matrices A,B,C are retrieved using a linear
least squares fit (Ljung, 1998). The covariance V of
the observation noise Z
k
can be estimated from data
as described in (Van Overschee and De Moor, 1994).
As in our BCG signal model measurements of the
input, the heart-beat times and forces, are not avail-
able, we use a bootstrap method for approximate sys-
tem identification: Heart beat excitations are approx-
imated with a signal derived from surface ECG mea-
surements. Specifically, we assume that the ECG sig-
nal is given for the first minute of our trial and use the
times of the R peaks in the QRS complexes as approx-
imate heart-beat times
˜
T
n
. In addition, α
n
≡ 1 is used
for all beats in (2). The synchronized BCG measure-
ments, correspond to the outputs Y
k
in (1). Currently,
our robust beat-detection algorithm is thus tailored
for setups where a state-space model representation is
known a-priori or setups that allow the use of our sug-
gested bootstrap system identification approach. The
input-output system identification is performed using
the N4SID algorithm (Van Overschee and De Moor,
1994) with a fixed system order.
Figure 2 demonstrates the approximation of a
single-channel BCG signal using a system order of
4, 8, and 14. The task of heart-beat detection, does
not require the BCG signal to be perfectly represented
by a state-space model: As shown in Section 4, 8-th
models, whose fit to the BCG data Figure 2 is clearly
inferior to higher order models, can still yield nearly
the same error-rate performance for heart-beat detec-
tion. Additionally, lower system orders are more ro-
bust with respect to variations of the BCG model (1)
and demand less computational resources.
2.1 Factor Graph of State-space Model
Since we model the BCG signals probabilistically,
our proposed algorithm relies heavily on probabilis-
tic inference methods. These computations can be
p
0
p
1
X
0
Y
1
U
1
p
2
X
1
Y
2
U
2
p
3
X
2
Y
3
U
3
···
X
3
Figure 3: Factor graph of initial part of the BCG signal
model.
performed by means of message passing on fac-
tor graphs. Factor graphs describe factorizations of
multi-variable functions(Kschischang et al., 2001).
As shown in (Loeliger et al., 2007), state-space mod-
els can also be represented with factor graphs and ef-
ficient algorithms for probabilistic inference, such as
maximum likelihood estimation and maximum a pos-
teriori estimation can then be derived.
In Forney-style factor-graph (FFG) nota-
tion (Kschischang et al., 2001), boxes represent
factors, whereas edges represent variables. A node
connected to several edges describes a function de-
pending on these variables. As an example, consider
the following factorization of the joint probability
model for Eq. (1), where a length M BCG signal is
observed,
p(y
1
,...,y
M
,x
0
,...,x
M
|u
1
,...,u
M
)
= p(x
0
) ·
M
∏
k=1
p(y
k
,x
k
|x
k−1
,u
k
).
(3)
The initial part of the FFG that corresponds to this fac-
torization is shown in Fig. 3, where the abbreviation
p
i
= p(y
i
,x
i
|x
i−1
,u
i
) was employed.
Each block p
i
in Fig. 3 can be expanded to the
factor shown in Fig. 4. The proposed algorithms are
based on the latter, more detailed, factorization.
Probabilistic inference (e.g., computation of
marginal probability densities for maximum a poste-
riori estimation) is performed by means of message
passing. In message passing algorithms, messages
µ are exchanged between nodes of the graph. Each
node computes output messages based on all incom-
ing messages. Marginal distributions can eventually
be obtained from the product of both messages on an
edge, which face in opposite direction. Central to the
development of our algorithm are forward messages
−→
µ
X
k
and backward messages
←−
µ
X
k
for state variables
X
k
. In particular, these messages represent
−→
µ
X
k
(x
k
) = p(y
1
,...,y
k−1
,x
k
|u
1
,...,u
k
) (4)
←−
µ
X
k
(x
k
) = p(y
k
,...,y
N
|x
k
,u
k+1
,...,u
N
). (5)
Sparse-inputDetectionAlgorithmwithApplicationsinElectrocardiographyandBallistocardiography
23

···
=
X
k−1
A
X
0
k−1
+
˜
X
k−1
B
˜
U
k
U
k
=
X
k
...
X
0
k
C
+
N (0,V )
Y
k
= y
k
Figure 4: One sample of the FFG of the linear state-space
model of BCG measurements.
Consequently, the product of these messages corre-
sponds to the probability density
−→
µ
X
k
(x
k
) ·
←−
µ
X
k
(x
k
) = p(y
1
,...,y
N
,x
k
|u
1
,...,u
N
). (6)
Given that the current model is a linear function
of Gaussian random variables and unknown deter-
ministic variables, inference of edge variables is per-
formed by means of Gaussian message-passing pre-
sented in (Loeliger et al., 2007). In this case, mes-
sages are Gaussian functionals
−→
µ
X
(x) = N (x|
−→
m
X
,
−→
V
X
) ·
−→
β
X
. (7)
These functionals are fully specified by the mean vec-
tor
−→
m , the covariance matrix
−→
V , and the scale fac-
tor
−→
β =
R
∞
−∞
−→
µ (x)dx. The computation rules for all
the nodes present in our FFG model (cf. Fig. 4),
are reported in the appendix. For ease of compu-
tations, an equivalent dual parametrization is com-
monly selected for the backward messages
←−
µ : The
messages are described using the inverse covariance
matrix
←−
W , the weighted mean
←−
W ·
←−
m and the scale
factor
←−
γ :=
←−
µ (0).
2.2 Heart-beat Time Estimation
Given a linear state-space model representation in (1)
and a sufficiently short multi-channel BCG segment,
the goal is to determine the heart-beat time T . The
main idea consists in performing a hypothesis test
over a time window of N observations and assessing
the likelihood that a heart-beat occurred in exactly one
specific position. For each point in time k ∈ {1, ..., N}
we have the hypothesis H
k
stating that all inputs in the
window, except the k-th are zero.
H
k
: U
j
=
(
u
k
, if j = k
0, else
(8)
To determine the position of the input via maximum
likelihood estimation in a hypothesis testing setting,
we will compute the likelihood of each hypothesis,
which is a function of the corresponding input magni-
tude
L
k
(u
k
) = p(y|H
k
,u
k
)
= p(y|U
1
= 0,...,U
k
= u
k
,...,U
N
= 0)
=
←−
µ
U
k
(u
k
)
(9)
We thus get the likelihood vector
~
L(~u) with:
~
L(~u) = (L
1
(u
1
),...,L
N
(u
N
))
T
(10)
Since
~
L is a vector valued function, we will integrate
out each input u
k
assuming a flat prior over the real or
positive real numbers
2
to reduce the likelihood func-
tions for each hypothesis to a single value.
¯
L
k
=
Z
∞
0
←−
µ
U
k
(u
k
)du
k
= 0.5·
←−
β
U
k
·erfc
−
←−
m
U
k
q
2
←−
V
U
k
(11)
To determine the beat position
ˆ
T , we select the index
of the most likely hypothesis
ˆ
T = argmax
k
¯
L
k
. (12)
The rationale behind this hypothesis test is to com-
pare how well the signal preceding the assumed input
is described by the state-space model in the absence
of an input and how well the oscillations following
the assumed input, fit to the model’s response to an
input. The robustness of this estimation procedure is
increased if the real heart beat is not too close to the
window’s borders. Estimation of the input magnitude
is done by means of maximum-a-posteriori estimation
using the posterior distribution of u
k
. The posterior
distribution, is computed taking a flat prior p(u
k
) as
in (11) and is proportional (i.e., a proportionality fac-
tor independent of u
k
) to
p(u
k
|H
k
,y) =
←−
µ
U
k
(u
k
). (13)
2
For the final algorithm we integrated over the positive
real numbers, which reflects the hypothesis that heart beats
are a positive impulses. This assumption leads to likeli-
hoods with less side peaks and thus to a more robust beat
detection
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
24
Consider the factor graph in Fig. 4 with hidden
states x = (x
0
,...,x
N
) and where each variable U
k
is
set to 0, thus expressing the probability density
p(y,x|U
1
= 0,...,U
N
= 0). (14)
To detect the heart beat time index, messages
←−
µ
U
k
(u
k
) for all possible k are computed in one foward
sweep and one backward sweep. It now follows that
the backward message
←−
µ
U
k
(u
k
) expresses
←−
µ
U
k
(u
k
) = p(y|U
1
= 0,...,U
k
= u
k
,...,U
N
= 0),
(15)
and using (11), with a flat prior on positive input am-
plitudes, the heart beat estimate
ˆ
T can be computed
from (12), as well as the input magnitude
u
MAP
k
=
(
←−
m
U
k
,
←−
m
U
k
≥ 0
0,
←−
m
U
k
< 0
. (16)
Note that computational complexity of this heart beat
time estimation is O(N), thus linear in the length of
the window.
2.3 Window-based Adaptive Beat
Detection
Having established an algorithm to estimate both the
input position and its magnitude given a time win-
dow containing one heart beat, the question that re-
mains is how to choose the windows properly to
cover the whole signal. Our approach was to use an
adaptive jumping window procedure. The bootstrap-
ping begins with a large window e.g. 2s such that
it contains at least one heart beat with high proba-
bility. The estimated position of that heart beat is
denoted as
ˆ
T
1
. Given an estimated heart beat posi-
tion
ˆ
T
k
, place a symmetric window around the posi-
tion where the next beat is assumed to be, denoted
as M
k+1
. Defining an average heart beat period as
HBP
k
= (
ˆ
T
k
−
ˆ
T
k−d
)/d, with d = 3 or d = 5 having
proved to yield good results
3
, and assuming an initial
HBP of 1 s, we get
M
k
=
ˆ
T
k−1
+ HPB
k−1
W
k
= [M
k
− bHBP
k−1
/2c,M
k
+ bHBP
k−1
/2c].
2.4 Automatic Artifact Detection
Movement artifacts can severely impair BCG mea-
surements and extraction of heart-beat times becomes
impossible. Initial system identification and reliable
estimation of heart-beat times both require that cor-
rupted signal segments are detected automatically. To
3
For the final implementation d = 3 was chosen
110 120 130 140
150 160
170
Time [s]
Amplitude a.u.
Figure 5: Prominent artifacts in the BCG signal, are labeled
(shaded) by the 6σ method.
this end, we devise a two-level approach. At first,
strong movement artifacts, which are characterized
by a much higher amplitude, are removed after pre-
processing of the measurements. This automatic de-
tection step, labels parts of the signal outside the 6-
sigma band
4
as artifacts. In a further step, short inter-
vals (< 0.5 s) between two adjacent labeled 6-sigma
bands, were also removed. In this way the BCG
signal is partitioned into useful signal intervals and
movements artifacts, which do not contain informa-
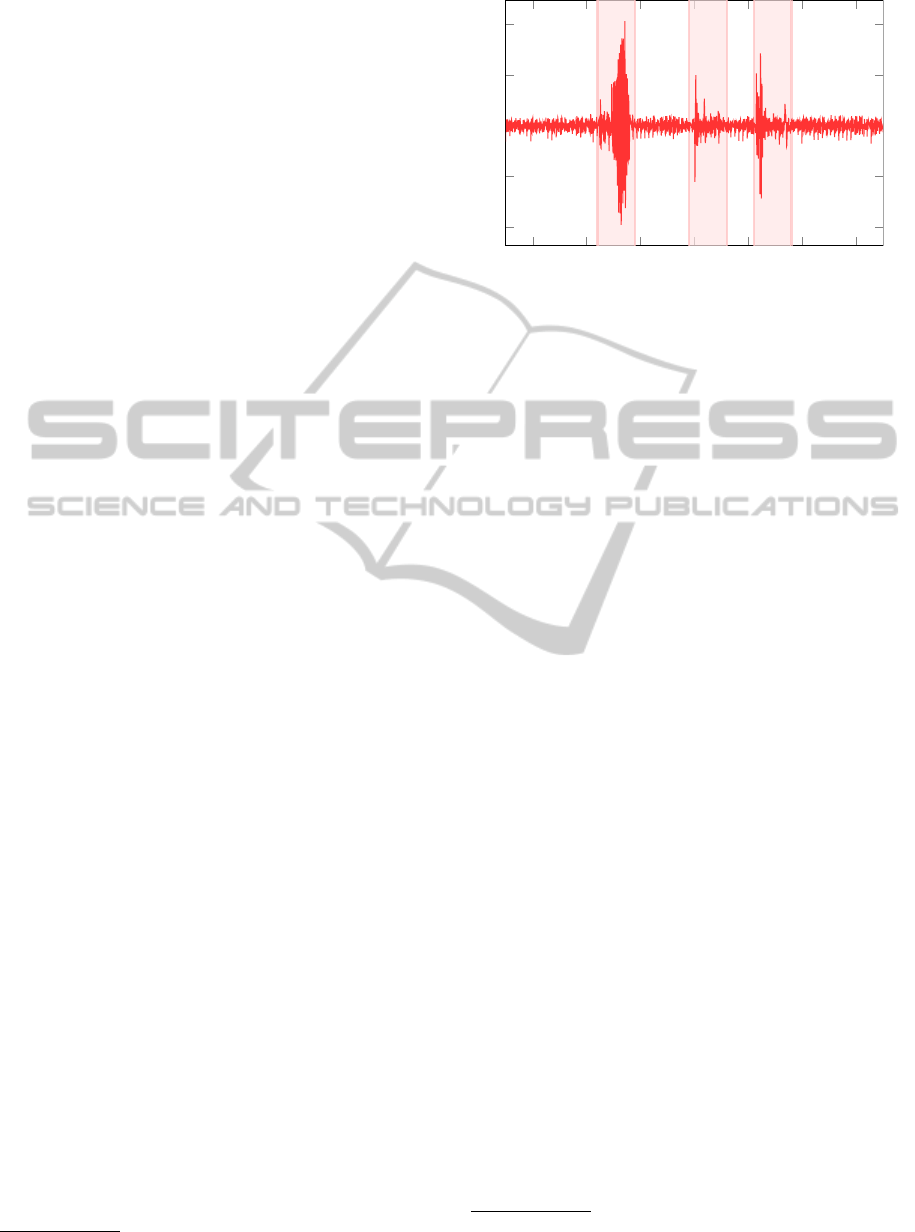
tion about the heart beats as can be seen in Figure 5.
The aforementioned labeling algorithm works
well, when movement artifacts are strong and have
a short duration (e.g. leg movements). In contrast,
a constant presence of small movement artifacts (e.g.
caused by tremor), would result in a very small vari-
ance of the signal and the movement-artifact detec-
tion algorithm would exclude parts of the signal with
slightly elevated amplitude from which the heart beats
could possibly still be extracted. For such signals, we
take advantage of the probabilistic modeling frame-
work: If a corrupted BCG segment is observed and
the model is not able to explain the data well, a sig-
nificant drop in the computed likelihood is observed.
The second level of our automatic artifact detection
method thus drops estimates
ˆ
T if the average likeli-
hood of the window drops below 50% the prior short-
time average likelihood values. Instead, the estimated
heart-beat time is predicted from past measurements
as
ˆ
T
k
=
ˆ
T
k−1
+ HPB
k−1
.
In Figure 6, false estimates are observed from sec-
ond 124 until second 126 caused by a small artifact,
which was not recognized by the 6σ method. How-
ever, the corresponding segment clearly exhibits a sig-
4
The 6-sigma band is defined as the amplitude values
falling in the interval of ±6σ + µ
Sparse-inputDetectionAlgorithmwithApplicationsinElectrocardiographyandBallistocardiography
25
120 122 124
126
128 130 132
Time [s]
ECG beats
estimated beats
Figure 6: Heart beat detection and input magnitude estima-
tion. Having no information about the instantaneous cardiac
output from the ECG data, we plot the heart beat magnitude
(black) as a uniform Dirac comb. Movement artifacts at
124s-126s cause midsections, which can be detected from
drops in the likelihood as shown in Figure 7
nificant drop in the average likelihood as shown in
Figure 7.
2.5 Post-processing
Following the recommendations of (Friedrich et al.,
2010), we assume a maximum average heart rate
5
of
120 BPM and a minimum heart rate of 30 BPM. Con-
sidering that heart rate measurements are supposed to
occur during rest these bounds are appropriate. These
averaging durations are in accordance with (Bruser
et al., 2011), which states that cardiac monitoring de-
vices can have an update time of up to 10s following
the recommendations of ANSI/AAMI/ISO EC13.
3 MATERIALS AND METHODS
To validate our heart-beat detection method we used
a dataset containing ECG measurements and two-
channel BCG measurements. The dataset comprises
12 healthy subjects (10 male, 2 female) in the age
range of 23-32 years. BCG signals were recorded
for 10 minutes in supine position (facing up), using
piezoelectric pressure sensors placed below the mat-
tress in the area where the torso was assumed to be.
Consequently, torso-ventral displacements, as defined
in (Scarborough et al., 1956), were measured. For val-
idation purposes, a three lead surface ECG synchro-
nized to the BCG signal was recorded. Instantaneous
heart rates ranged from 33 BPM and up to 88 BPM
across all 12 subjects.
5
The average heart rate is computed by taking the aver-
age over 5 consecutive beats.
Likelihood
Figure 7: Movement artifacts are detected by drops in like-
lihood values. The corrupted signal is recognized and cor-
rected assuming a constant average heart rate. This refine-
ment increases stability and reduces the average heart beat
detection error rate.
290 300 310 320 330 340
70
75
80
Time [s]
Beats per minute
actual heart rate
estimated heart rate
Figure 8: Real ECG-based instantaneous heart rate com-
pared to the instantaneous heart rate extracted from the es-
timated heart-beat times of our method.
3.1 Pre-processing of BCG and ECG
Measurements
Prior to our algorithm, the BCG signal was deci-
mated
6
from 1000 Hz to 200 Hz primarily to reduce
computational costs and also noise. A 10-th order,
zero-phase bandpass filter (0.5Hz-30Hz) was com-
bined with a second-order IIR notch filter at 50 Hz,
using the DSP System toolbox in MATLAB 2014a, to
remove respiratory movements and to remove strong
electrical disturbances at 50 Hz. The ECG signal was
high-pass filtered with a 5-th order Butterworth filter
at 2 Hz cut-off to remove baseline wandering. Heart
beats were then extracted via peak detection from the
filtered ECG signal.
4 PERFORMANCE EVALUATION
The proposed beat-to-beat estimation algorithm was
validated using ECG measurements as ground truth
in the following way: The ECG heart beat train, con-
taining M heart beats, was split into M segments. The
segments are chosen such that each one contains ex-
actly one heart-beat and their union covers the whole
ECG signal. Given heart beats at times T
k−1
, T
k
and
6
Downsampling and anti-alias filtering
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
26

T
k+1
, the k-th segment s
k
is defined as
s
k
= [T
k
− b(T
k
− T
k−1
)/2c,T
k
+ b(T
k+1
− T
k
)/2c].
The estimate
ˆ
T
k
is counted as correct, if exactly one
beat was detected and
ˆ
T
k
∈ [T
k
− 25ms, T
k
+ 25ms].
Note that the duration between the electrical activa-
tion and the actual blood ejection displays a varia-
tion of around 8 ms (Friedrich et al., 2010) and thus,
is the maximum precision a beat localization using
BCG measurements can achieve. Assuming an aver-
age window length of 1 s, corresponding to 60 BPM,
the
ˆ
T
k
is required to have a precision of ±2.5%.
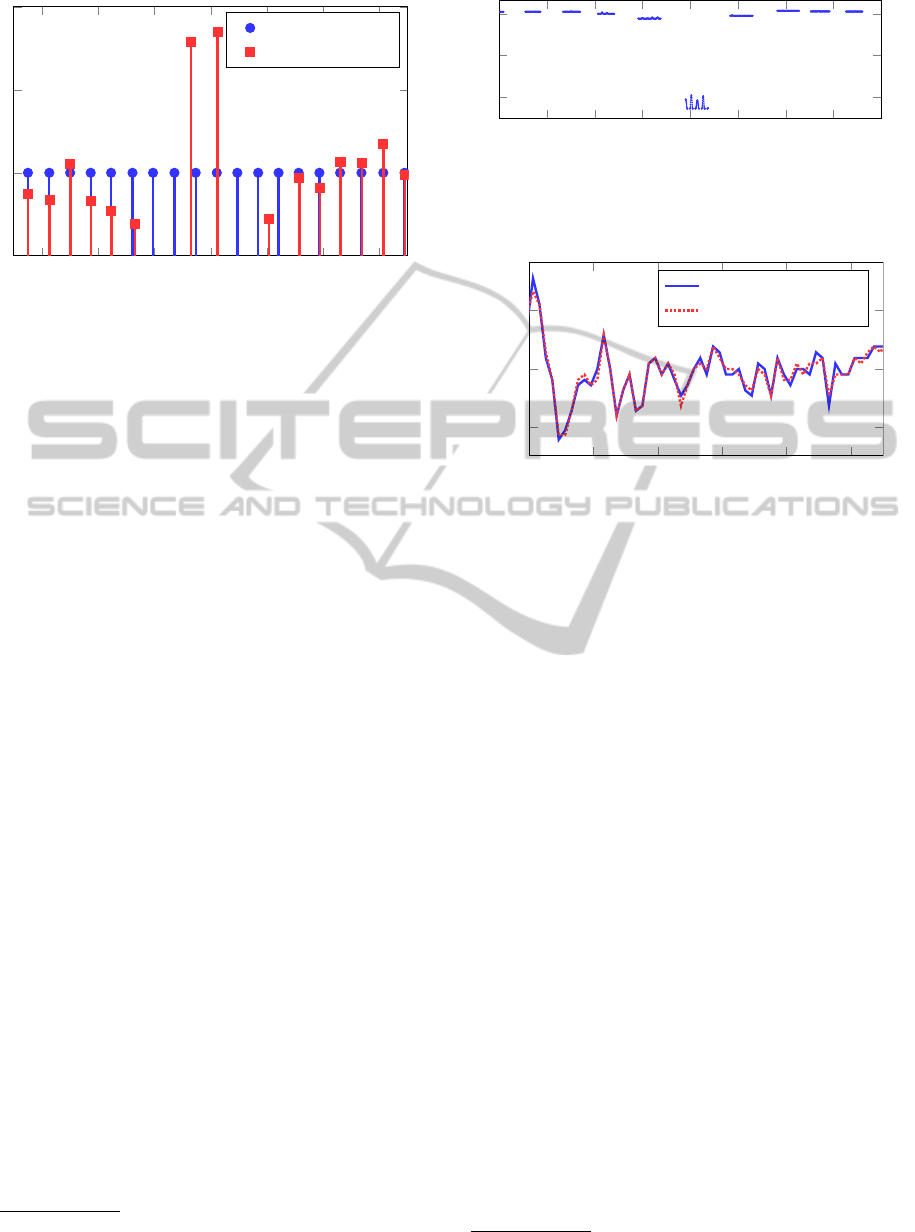
Figure 9 shows the heart beat detection error rate
as a function of even system orders
7
of the state space
model used to describe the BCG signal of subject A.
We can see that too low system orders are not suited
for modeling the BCG signal and lead to very high
error rates. Two channel measurements outperform
single channel measurements for almost all system or-
ders except for very low system orders (2 and 4), for
which it is better to use single channel measurements,
due to the lower complexity of the model required to
describe the single channel measurements. The in-
creasing error rate with system order above 20 could
be hinting to overfitting, when system orders are too
high. On the other hand it is also possible that numer-
ical precision issue arise when performing message
passing in factor graphs of state space models of such
high order.
The error-rate performance of the presented
method is evaluated with two 10 minutes long bal-
listocardiogram recordings of 12 healthy subjects, ex-
cluding sections of the signal containing movement
artifacts, which do not provide information about the
heart-beat times. The resulting error rate, averaged
over the test subjects, is 4.7% with a standard er-
ror of the mean of 2.8%. A 14-th order state-space
representation is used to describe the BCG signal.
These performance metrics include one outlier sub-
ject, whose BCG signal contains multiple movement
artifacts, leading to an error rate of 35%. Excluding
the outlier, the mean error rate decreases to 3.4% with
a standard error of the mean of 1.3%.
Automatic artifact detection on the present dataset
results in an average estimation coverage for each
channel, thus the percentage of the signal or windows
not detected as corrupted by movement artifacts. Af-
ter the first 6σ labeling method the average coverage
is 95%. Subsequent detection using the likelihood-
based method (see Section 2.4), additionally drops
5% of the windows. Therefore reducing average cov-
erage to around 90%.
7
Even system orders describe the output signal solely as
a linear combination of exponentially decaying oscillations
2 4
6
8 10 12 14
16
18 20 22 24
26
0
20
40
60
80
System order
Error rate [%]
one channel
two channels
Figure 9: Heart beat detection error rate for subject A as
a function of the system order for single and two-channel
measurements.
Figure 8 compares the beat-to-beat (instanta-
neous) heart rate extracted from ECG and from the
estimates
ˆ
T of the suggested method. The estimated
heart-beat times reveal even small fluctuations in the
beat-to-beat times. The average interval error be-
tween actual heart beats (ECG) and estimated heart
beats was computed according to (Friedrich et al.,
2010) resulting in an average heart beat interval error
of 33.1 ms. Note that the average heart beat detection
error rate, introduced above, is better suited to assess
our algorithm, as it identifies single heart beats (i.e.,
beat detection and time
ˆ
T
k
) and not the intervals be-
tween heart beats.
The heart beat detection algorithm takes around
60 s to estimate instantaneous heart rates in a 10 min-
utes long two-channel BCG signal using MATLAB
R2014a on a 3.33 GHz, 8 GB personal computer, in-
cluding system estimation, loading of data and pre-
processing. The pure heart beat estimation takes
around 35 s, for the 10 minutes long BCG sequences,
thus when allowing a small delay (e.g. 5 s) and a start
up-time for 30 s the algorithm could run in real time,
especially when implemented in faster programming
languages such as C/C++.
5 DISCUSSION AND
CONCLUSIONS
We have presented a novel method to extract beat-
to-beat data from ballistocardiograms. Given an es-
timated or known linear state-space model represen-
tation of the ballistocardiogram signal, heart beats are
extracted from measured data using a robust input-
estimation algorithm. We have shown that additional
measurement channels (i.e., multiple sensors) yield
significant performance improvements in terms of
error-rate and robustness. Owing to the model-based
approach, the method can correctly extract movement
Sparse-inputDetectionAlgorithmwithApplicationsinElectrocardiographyandBallistocardiography
27

artifacts from measured data and recognize when beat
detection is impaired or not possible. Validation of the
method on ballistocardiogram measurements of 12
healthy subjects showed 4.7% average beat-detection
error rate. The presented algorithm lends itself to ap-
plication on a multitude of almost periodic signals,
especially in cardiology.
Currently, the algorithm at first adapts itself to a
specific BCG signal, as described in Section 2. It
is likely that alterations of the system (e.g., changed
body position) will trigger the likelihood-based arti-
fact detection routine (see Section 2) and a new sys-
tem identification step will become necessary. How-
ever, in the present dataset, subjects were laying still
and this issue was not observed.
A further complication, which was also not ob-
served in the current dataset, may arise when strong
heart-rate variability occurs. The window-based ap-
proach may either select a window where no beat
is present or a window with two beats. In the first
case, a false-positive beat will be detected, while in
the other case, the algorithm will miss a beat and
make a false-negative error. This issue could be ad-
dressed by considering the relative likelihood value
of a beat estimate to the other indices with large like-
lihood values and deciding if two beats are present or
none. Also schemes which run the window-based de-
tection schemes multiple times and each time includ-
ing the currently detected beats and models on heart-
rate variability might mitigate these type of errors.
Blind system identification i.e., estimation of the
state-space model solely on BCG measurements,
would facilitate applicability of the current method.
As a consequence, the resulting method would not
require ECG measurement equipment and would be
able to adapt to varying external factors (e.g., sleeping
position). Moreover, investigating on the relation be-
tween the estimated input magnitude and the instan-
taneous cardiac output, which is a key biomarker for
various cardiovascular diseases, seems to be a promis-
ing direction for future research.
A further enhancement can be achieved by multi-
plying the hypothesis likelihood with a Gaussian win-
dow, centered around the assumed input, serving as
a prior on the heart beat position. This refinement
significantly improves error rates, when the BCG sig-
nal is hardly contaminated by movement artifacts. On
the other hand when the signal contains several move-
ment artifacts, it is better not to assume any prior on
the beat position to avoid error propagation. To deal
with a general BCG signal, possibly heavily contam-
inated with artifacts, the Gaussian window was omit-
ted in the performance evaluation in subsection 4.
Table 1: Performance metrics.
Metric Unit Value
Signal duration min 10
Coverage 6-σ labeling % 95
Coverage likelihood drop labeling % 90
HB detection error rate % 4.7
HB interval error ms 33.1
ACKNOWLEDGEMENTS
The authors would like to thank Nour Zalmai for valu-
able feedback concerning the sparse-input learning al-
gorithm. Furthermore we highly appreciated the valu-
able discussions with Dr. med. Reto Wildhaber re-
garding the cardiovascular system.
REFERENCES
Alihanka, J., Vaahtoranta, K., and Saarikivi, I. (1981). A
new method for long-term monitoring of the ballisto-
cardiogram, heart rate, and respiration. Am J Physiol,
240(5):R384–92.
Bruser, C., Stadlthanner, K., de Waele, S., and Leonhardt,
S. (2011). Adaptive beat-to-beat heart rate estimation
in ballistocardiograms. IEEE Transactions on Infor-
mation Technology in Biomedicine,, 15(5):778–786.
Cathcart, R. T., Field, W. W., and Richards Jr, D. W. (1953).
Comparison of cardiac output determined by the bal-
listocardiograph (nickerson apparatus) and by the di-
rect fick method. Journal of Clinical Investigation,
32(1):5.
Friedrich, D., Aubert, X., Fuhr, H., and Brauers, A.
(2010). Heart rate estimation on a beat-to-beat ba-
sis via ballistocardiography-a hybrid approach. In En-
gineering in Medicine and Biology Society (EMBC),
2010 Annual International Conference of the IEEE,
pages 4048–4051. IEEE.
Inan, O., Etemadi, M., Paloma, A., Giovangrandi, L., and
Kovacs, G. (2009). Non-invasive cardiac output trend-
ing during exercise recovery on a bathroom-scale-
based ballistocardiograph. Physiological measure-
ment, 30(3):261.
Kschischang, F. R., Frey, B. J., and Loeliger, H.-A. (2001).
Factor graphs and the sum-product algorithm. In-
formation Theory, IEEE Transactions on, 47(2):498–
519.
Kurumaddali, B., Marimuthu, G., Venkatesh, S. M., Suresh,
R., Syam, B., and Suresh, V. (2014). Cardiac output
measurement using ballistocardiogram. In The 15th
International Conference on Biomedical Engineering,
pages 861–864. Springer.
Ljung, L. (1998). System identification. Springer.
Loeliger, H.-A., Dauwels, J., Hu, J., Korl, S., Ping, L., and
Kschischang, F. R. (2007). The factor graph approach
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
28

to model-based signal processing. Proceedings of the
IEEE, 95(6):1295–1322.
Mack, D. C., Patrie, J. T., Suratt, P. M., Felder, R. A., and
Alwan, M. (2009). Development and preliminary val-
idation of heart rate and breathing rate detection using
a passive, ballistocardiography-based sleep monitor-
ing system. Information Technology in Biomedicine,
IEEE Transactions on, 13(1):111–120.
Paalasmaa, J., Toivonen, H., and Partinen, M. (2014). Adap-
tive heartbeat modelling for beat-to-beat heart rate
measurement in ballistocardiograms. IEEE Journal
of Biomedical and Health Informatics,, PP(99):1–1.
Reller, C. (2012). State-space methods in statistical signal
processing: New ideas and applications. PhD thesis,
ETH Zurich.
Scarborough, W. R., Talbot, S. A., Braunstein, J. R., Rap-
paport, M. B., Dock, W., Hamilton, W., Smith, J. E.,
Nickerson, J. L., and Starr, I. (1956). Proposals for
ballistocardiographic nomenclature and conventions:
revised and extended report of committee on ballis-
tocardiographic terminology. Circulation, 14(3):435–
450.
Schnittger, I., Rodriguez, I. M., and Winkle, R. A. (1986).
Esophageal electrocardiography: a new technology
revives an old technique. The American journal of
cardiology, 57(8):604–607.
Shin, J., Choi, B., Lim, Y., Jeong, D., and Park, K. (2008).
Automatic ballistocardiogram (bcg) beat detection us-
ing a template matching approach. In Engineering
in Medicine and Biology Society, 2008. EMBS 2008.
30th Annual International Conference of the IEEE,
pages 1144–1146.
Van Overschee, P. and De Moor, B. (1994). N4sid:
Subspace algorithms for the identification of com-
bined deterministic-stochastic systems. Automatica,
30(1):75–93.
Van Overschee, P. and De Moor, B. (1996). Subspace iden-
tification for linear systems: Theory, implementation.
Methods.
Watanabe, K., Watanabe, T., Watanabe, H., Ando, H.,
Ishikawa, T., and Kobayashi, K. (2005). Noninva-
sive measurement of heartbeat, respiration, snoring
and body movements of a subject in bed via a pneu-
matic method. Biomedical Engineering, IEEE Trans-
actions on, 52(12):2100–2107.
Yelderman, M. and New Jr, W. (1983). Evaluation of pulse
oximetry. Anesthesiology, 59(4):349–351.
Yusuf, S., Reddy, S.,
ˆ
Ounpuu, S., and Anand, S. (2001).
Global burden of cardiovascular diseases part i: gen-
eral considerations, the epidemiologic transition, risk
factors, and impact of urbanization. Circulation,
104(22):2746–2753.
APPENDIX
Message Passing
Measurements are plugged into the factor graph, re-
sulting in Dirac delta messages. Let X
k
∈ R
n
and
Y
k
∈ R
p
←−
m
Y
k
=y
k
←−
V
Y
k
=0
←−
β
Y
k
=1
←−
µ
Y
k
(y
k
)=δ(y
k
− y
obs
k
)
Sum-product message passing through the sum-factor
(
˜
Y
k
+ Z
k
).
←−
W
˜
Y
k
=V
−1
←−
W
˜
Y
k
←−
m
˜
Y
k
=V
−1
y
k
←−
β
˜
Y
k
=
←−
β
Y
k
·
−→
β
Z
k
= 1
←−
µ
˜
Y
k
( ˜y
k
)=(2π)
−
p
2
det(V )
−
1
2
e
−
1
2
( ˜y
k
−y
k
)
T
V
−1
( ˜y
k
−y
k
)
←−
µ
˜
Y
k
(0) =
←−
γ
˜
Y
k
= (2π)
−
p
2
det(V )
−
1
2
e
−
1
2
y
T
k
V
−1
y
k
←−
W
X
00
k
=C
0
←−
W
˜
Y
C
←−
W
X
00
k
←−
m
x
00
k
=C
0
←−
W
˜
Y
k
←−
m
˜
Y
k
←−
γ
X
00
k
=
←−
γ
˜
Y
k
Forward Message Passing
Forward message passing corresponds to Kalman fil-
tering in the state space model. The update equations
are
m
X
0
k
=
−→
m
X
k
+
−→
V
X
k
C
T
G(
←−
m
˜
Y
k
−C
−→
m
X
k
)
−→
V
X
0
k
=
−→
V
X
k
−
−→
V
X
k
C
T
GC
−→
V
X
k
G
−1
=
←−
V
˜
Y
k
+C
−→
V
X
k
C
T
V : =
←−
V
˜
Y
k
+C
−→
V
X
k
C
T
m : =C
−→
m
X
k
+
←−
m
˜
Y
k
−→
β
X
0
k
=
−→
β
X
k
←−
β
˜
Y
k
s
1
(2π)
p
· det(V )
e
−
m
T
V
−1
m
2
−→
m
˜
X
k
=A
−→
m
X
0
k
−→
V
˜
X
k
=A
−→
V
X
0
k
A
T
−→
β
˜
X
k
=
−→
β
X
0
k
Sparse-inputDetectionAlgorithmwithApplicationsinElectrocardiographyandBallistocardiography
29

−→
m
X
k+1
=
−→
m
˜
X
k
−→
V
X
k+1
=
−→
V
˜
X
k
−→
β
X
k+1
=
−→
β
˜
X
k
Backward Message Passing
Backward message passing corresponds to Kalman
smoothing in the state space model. The update equa-
tions are
←−
W
X
k
=
←−
W
X
00
k
+
←−
W
X
0
k
←−
W
X
k
←−
m
X
k
=
←−
W
X
00
k
←−
m
X
00
k
+
←−
W
X
0
k
←−
m
X
0
k
←−
γ
X
k
=
←−
γ
X
0
k
←−
γ
X
00
k
←−
β
X
k
=
←−
γ
X
k
s
(2π)
n
det(
←−
W
X
k
)
e
←−
m
X
k
←−
W
X
k
←−
m
X
k
/2
←−
W
X
0
k
=A
T
←−
W
˜
X
k
A
←−
W
X
0
k
←−
m
X
0
k
=A
T
←−
W
˜
X
k
←−
m
˜
X
k
←−
γ
X
0
k
=
←−
γ
˜
X
k
Rejoining Messages
To determine the marginal distribution of U
k
we com-
bine the forward and backward messages.
←−
m
˜
U
k+1
=
←−
m
X
k+1
−
−→
m
˜
X
k
←−
V
˜
U
k+1
=
←−
V
X
k+1
+
−→
V
˜
X
k
←−
β
˜
U
k+1
=
−→
β
˜
X
k
←−
β
X
k+1
For the heart beat estimation problem we assume that
the input is scalar.
←−
W
U
k
=B
T
←−
W
˜
U
k
B
←−
W
U
k
←−
m
U
k
=B
T
←−
W
˜
U
k
←−
m
˜
U
k
←−
β
U
k
=
←−
β
˜
U
k
s
1
(2π)
n−1
v
u
u
t
det(
←−
V
U
k
)
det(
←−
V
˜
U
k
)
e
−
←−
m
T
˜
U
k
←−
W
˜
U
k
V
←−
W
˜
U
k
←−
m
˜
U
k
/2
V : =
←−
V
˜
U
k
− B
←−
V
U
k
B
T
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
30
