
oADABOOST
An ADABOOST Variant for Ordinal Classification
Jo
˜
ao Costa
1
and Jaime S. Cardoso
2
1
Faculdade de Engenharia, Universidade do Porto, Rua Dr. Roberto Frias, 4200-465 Porto, Portugal
2
INESC TEC and Faculdade de Engenharia, Universidade do Porto,
Rua Dr. Roberto Frias, n
o
378, 4200-465 Porto, Portugal
Keywords:
Supervised Learning, Ordinal Classification, Ensemble Methods, ADABOOST.
Abstract:
Ordinal data classification (ODC) has a wide range of applications in areas where human evaluation plays an
important role, ranging from psychology and medicine to information retrieval. In ODC the output variable
has a natural order; however, there is not a precise notion of the distance between classes. The Data Repli-
cation Method was proposed as tool for solving the ODC problem using a single binary classifier. Due to
its characteristics, the Data Replication Method is straightforwardly mapped into methods that optimize the
decision function globally. However, the mapping process is not applicable when the methods construct the
decision function locally and iteratively, like decision trees and ADABOOST (with decision stumps). In this
paper we adapt the Data Replication Method for ADABOOST, by softening the constraints resulting from the
data replication process. Experimental comparison with state-of-the-art ADABOOST variants in synthetic and
real data show the advantages of our proposal.
1 INTRODUCTION
One of the most representative problems of super-
vised learning is classification, consisting of the es-
timation of a mapping from the feature space into a
finite class space. Depending on the cardinality of
the output space, we are left with binary or multiclass
classification problems. Finally, the presence or ab-
sence of a “natural” order among classes differenti-
ates nominal from ordinal problems.
A large number of real world classification prob-
lems can be seen as ordinal tasks, that is, we want
to learn a function that is able to classify points in a
finite set of classes, which have an ordering relation
between them (e.g. we might want to classify a movie
as good, average or bad).
Note that, since only the order is known, one can-
not simply pick an arbitrary mapping from our classes
to numbers (e.g. bad 7→ 0, average 7→ 1, good 7→ 2)
and solve a regression problem, as our error function
would be highly dependent of that mapping. Also,
our classes might not have a valid numerical interpre-
tation, (e.g. is a good movie equivalent to two average
movies?) therefore choosing an appropriate mapping
is not trivial.
One solution to ordinal problems is to simply ig-
nore the ordering relation, treat them as nominal clas-
sification problems and use a learning algorithm de-
signed for this kind of tasks (e.g. C4.5 decision trees
and ADABOOST). A better alternative is to devise so-
lutions that take advantage of the order information
in the design of the classifier. A possible approach is
to transform our dataset in such a way that we force
our learning algorithm to respect the ordering rela-
tion. One such transformation is the Data Replication
Method (Cardoso and da Costa, 2007), which trans-
forms an ordinal problem into a larger binary clas-
sification one. One of the limitations of the Data
Replication Method is that it cannot be immediately
applicable when the decision function is constructed
iteratively and locally, like in decision trees or AD-
ABOOST.
In this work, we present a new ADABOOST vari-
ant that performs its growth on the replicated feature
space, and therefore is able to use the ordering rela-
tion when training the weak classifiers.
1.1 Related Work
Frank and Hall presented a simple method that en-
ables standard classification algorithms to make use
of ordering information in class attributes (Frank and
68
Costa J. and Cardoso J..
oAdaBoost - An AdaBoost Variant for Ordinal Classification.
DOI: 10.5220/0005191600680076
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 68-76
ISBN: 978-989-758-076-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Hall, 2001). By applying it in conjunction with a deci-
sion tree learner, the authors show that it outperforms
the naive approach, which treats the class values as
an unordered set. Compared to special-purpose algo-
rithms for ordinal classification, the method has the
advantage that it can be applied without any modi-
fication to the underlying learning scheme. The ra-
tionale encompasses using (K − 1) standard binary
classifiers to address the K-class ordinal data prob-
lem. Toward that end, the training of the i-th clas-
sifier is performed by converting the ordinal dataset
with classes C
1
, . . . , C
K
into a binary dataset, discrim-
inating C
1
, . . . , C
i
against C
i+1
, . . . , C
K
. To predict the
class value of an unseen instance, the (K − 1) outputs
are combined to produce a single estimation. Any bi-
nary classifier can be used as the building block of
this scheme. Observe that the (K − 1) classifiers are
trained in an independent fashion. This independence
is likely to lead to intersecting boundaries, a topic to
which we will return further on in this paper.
The Data Replication Method (Cardoso and
da Costa, 2007) overcomes the limitations identified
above by building all the boundaries at once. That
guarantees that the boundaries of the classifiers will
never intersect. This method, however, has limitations
with methods that build the decision function itera-
tively (and greedily), and therefore cannot be easily
mapped to ADABOOST.
In the ensemble approach to ordinal data classi-
fication, although not directly related to our work, it
is worth mentioning the work introducing global con-
straints in the design of decision trees (Cardoso and
Sousa, 2010; Sousa and Cardoso, 2011). The method
consists on growing a tree (or an ensemble of trees)
and relabeling the leaves according to certain con-
straints. Therefore, the trees are still built without
taking the order into account and only post-processed
to satisfy ordinality constraints. Moreover, the post-
processing is very computationally demanding, only
possible in low dimensional input spaces. More re-
cently, the combination of multiple orthogonal direc-
tions has been suggested to boost the performance of
a base classifier (Sun et al., 2014). Sequentially, mul-
tiple orthogonal directions are found; these different
directions are combined in a final stage.
There are also some boosting-related approaches
for ordinal ranking. For example, RankBoost (Fre-
und et al., 2003) approach is based on the pairwise
comparison perspective. Lin and Li proposed or-
dinal regression boosting (ORBoost) (Lin and Li,
2006), which is a special instance of the extended bi-
nary classification perspective. The ensemble method
most in line with our work is ADABOOST.OR (Lin
and Li, 2009). This method uses a primal-dual ap-
proach to solve an ordinal problem both in the bi-
nary space and the ordinal space, by taking into ac-
count the order relation when updating the binary
point’s weights. However, ADABOOST.OR is more
constrained than our proposed approach; while AD-
ABOOST.OR is closer to a single ADABOOST instan-
tiated with an ordinal data classifier, our approach is
closer to having multiple ADABOOST coupled in the
construction of the weak classifier.
2 BACKGROUND
In this section we start by analysing the Frank and
Hall’s approach to ordinal classification (Frank and
Hall, 2001), which facilitates the introduction of the
Data Replication Method (Cardoso and da Costa,
2007). The Data Replication Method is a framework
for ordinal data classification that allows the applica-
tion of most binary classification algorithms to ordinal
classification and imposes a parallelism constraint on
the resulting boundaries. In the end, we summarize
the ADABOOST ensemble method, paving the way to
the presentation of the proposed adaptation of AD-
ABOOST to ordinal data.
2.1 Frank and Hall Method
Suppose we want to learn a function f : X → Y ,
where X is our feature space and Y =
{
C
1
, C
2
, ..., C
K
}
is our output space, where our labels are ordered ac-
cording to C
1
≺ C
2
≺ ... ≺ C
K
. Also, assume that we
have a dataset D = (D, f ), where D ⊆ X is our set of
examples and f : D → Y gives us the label of each
example.
The Frank and Hall method transforms the K class
ordinal problem into (K − 1) binary problems by cre-
ating (K − 1) datasets D
k
= (D, f
k
) where:
f
k
(x) =
(
C
−
if f (x) C
k
C
+
if f (x) C
k
Intuitively, learning a binary classifier from each
of the D
k
datasets will create (K − 1) classifiers that
answer the questions “is the label of point x larger
than C
k
?”. This is to say, each classifier will give us
an estimate of P( f (x) C
k
).
Frank and Hall then propose that one finds the
P( f (x) = C
k
) using the usual rule:
1 − P( f (x) C
1
) if k = 1
P( f (x) C
k−1
) − P( f (x) C
k
) if k ∈ [2, K − 1]
P( f (x) C
K−1
) if k = K
oAdaBoost-AnAdaBoostVariantforOrdinalClassification
69

Even though our conversion from ordinal to bi-
nary guarantees that f
k
(x) = C
−
⇒ f
k+1
(x) = C
−
and
f
k
(x) = C
+
⇒ f
k−1
(x) = C
+
, those rules do not al-
ways hold for the learnt probabilities. In practice,
this means that it is possible that the combination
rule proposed by Frank and Hall returns a negative
probability for some classes. One solution to this
problem is setting that negative probabilities to zero.
Another possible way to combine our binary classi-
fiers is by a simple counting method:
ˆ
f (x) = C
i
, with
i = 1 +
∑
K−1
k=1
[[ f
k
(x) = C
+
]]
1
. In either way, the main
conceptual problem is not addressed.
2.2 Consistency and Parallelism
One important concept in ordinal data classification is
the idea of consistency with the ordinal setting (Car-
doso and Sousa, 2010). The idea behind it is intu-
itive: a small change in the input data should not lead
to a ‘big jump’ in the output decision (e.g. it is not
expected that a small change in a feature makes the
estimated product quality to go from “bad” to “good”
without going through “average”). One way to guar-
antee this restriction is by enforcing that there is no
intersection between decision boundaries, which can,
in turn, be guaranteed by enforcing our boundaries to
be parallel.
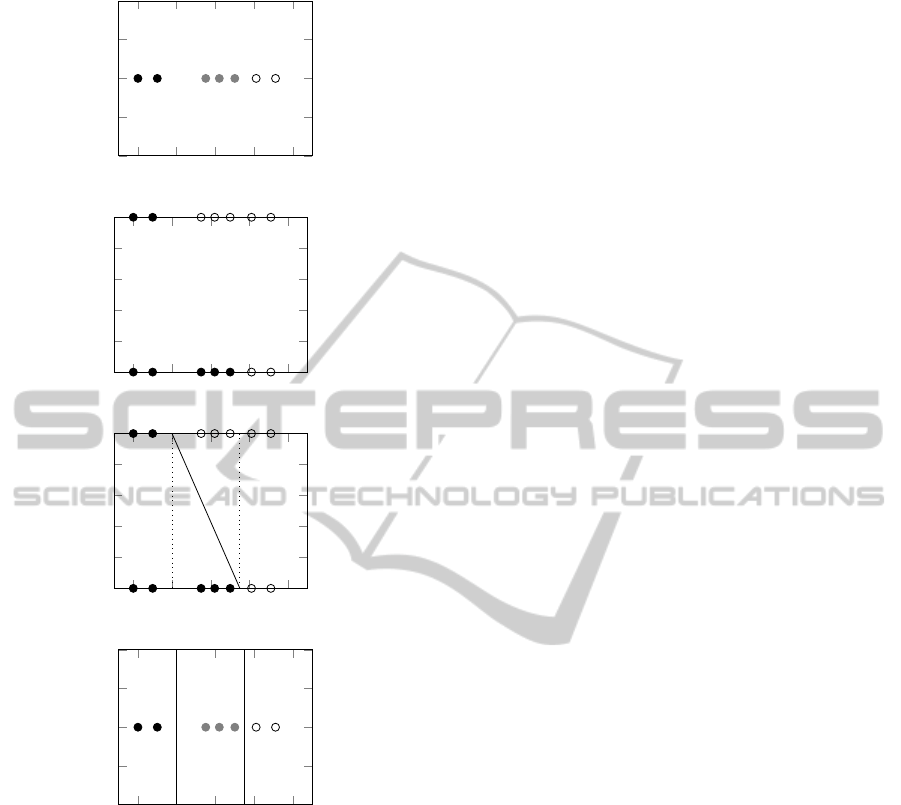
In Figure 1 it is possible to see two partitions of the
input space corresponding to two different classifiers,
one without the parallelism constraint and another one
with it. In the first one, a small variation around the
point marked with
N
can make an abrupt jump be-
tween two very distinct classes (“black” and “white”),
while on the second classifier that is not possible.
It can be seen that the method proposed by Frank
and Hall does not respect this concept, and therefore
can lead to problematic classifiers.
2.3 The Data Replication Method
The Data Replication Method uses the idea behind the
Frank and Hall method in a different way: instead of
simply creating (K −1) datasets, it extends the feature
space so that all points from the (K − 1) replicas are
present on the same dataset.
Assume e
0
as a vector composed of (K − 2) ze-
ros and a vector e
q
as a vector composed by (K − 3)
zeros and a positive constant (e.g. 1) on the q-th posi-
tion (e.g. if K = 5, e
2
= [0, 1, 0]). We then transform
each point x ∈ D into (K −1) points z
q
= (x, e
q
). This
does allows us to train a single binary classifier on the
whole data and then combine the results in the same
1
[[·]] is the indicator function. [[·]] is 1 if the inner condi-
tion is true, 0 otherwise.
0 1 2 3 4
0
1
2
3
4
(a)
0 1 2 3 4
0
1
2
3
4
(b)
Figure 1: Comparison of a (a) non-consistent multiclass
classifier vs. (b) a multiclass classifier with parallelism con-
straints
fashion as previously presented. Also, this replication
guarantees that some algorithms such as Suport Vec-
tor Machines (SVMs) and Artificial Neural Networks
(ANNs) will always produce parallel boundaries on
the final ordinal space. A simple example of the Data
Replication Method can be seen in Figure 2. Note
that: a) x ∈ R while z ∈ R
2
; b) a single binary clas-
sifier is designed in the extended dataset to solve the
multiclass problem in the original space. The inter-
section of the binary boundary with each of the K − 1
replicas provide the necessary K −1 boundaries in the
original space. Further details of the method can be
found on the original paper (Cardoso and da Costa,
2007).
2.4 ADABOOST
ADABOOST is a boosting algorithm introduced by
Freund and Schapire (Freund and Schapire, 1995).
Boosting algorithms are a part of a big set of machine
learning techniques called ensemble methods which
general idea is to use several models to classify obser-
vations and combine them together to obtain a classi-
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
70
−4 −2 0 2 4
−1
−0.5
0
0.5
1
(a)
−4 −2 0 2 4
0
0.2
0.4
0.6
0.8
1
(b)
−4 −2 0 2 4
0
0.2
0.4
0.6
0.8
1
(c)
−4 −2 0 2 4
−1
−0.5
0
0.5
1
(d)
Figure 2: Toy example of the Data Replication Method. (a)
Original Problem. (b) Problem on the replicated space. (c)
Solution to the problem on the replicated space. (d) Result
on the original space.
fier with a predictive performance superior than any
of its constituents. ADABOOST uses a weak learner
to classify observations. A weak learner is defined as
a classifier which is only slightly correlated with the
true data labels. In the case of binary prediction, a
weak learner is a classifier which is only slightly bet-
ter than throwing a coin and deciding an object’s class
according to the trial’s result.
During each iteration, the algorithm trains a weak
learner
ˆ
f
t
(x) using an iteratively determined distribu-
tion and selects the weak hypothesis minimizing the
expected error rate. After selecting the best weak hy-
pothesis
ˆ
f
t
for the distribution D
t
, the observations
x
i
correctly identified by
ˆ
f
t
are weighted less than
those misclassified, so that the algorithm will, when
fitting a new weak hypothesis to D
t+1
in the next it-
eration, select one such rule which identifies better
those observations that its predecessor failed. The
output of the ADABOOST algorithm is a final or com-
bined hypothesis
ˆ
f
F
.
ˆ
f
F
is simply the sign of a
weighted combination of the weak hypothesis, i.e.,
H is a weighted majority rule of the weak classifiers,
ˆ
f
F
(x) = sign
∑
T
t=1
α
t
ˆ
f
t
(x)
.
3 oADABOOST
While the Data Replication Method (DRM) has al-
ready been instantiated with SVMs, ANNs and Kernel
Discriminant Analysis (Cardoso and da Costa, 2007;
Cardoso et al., 2012), its mapping to ADABOOST
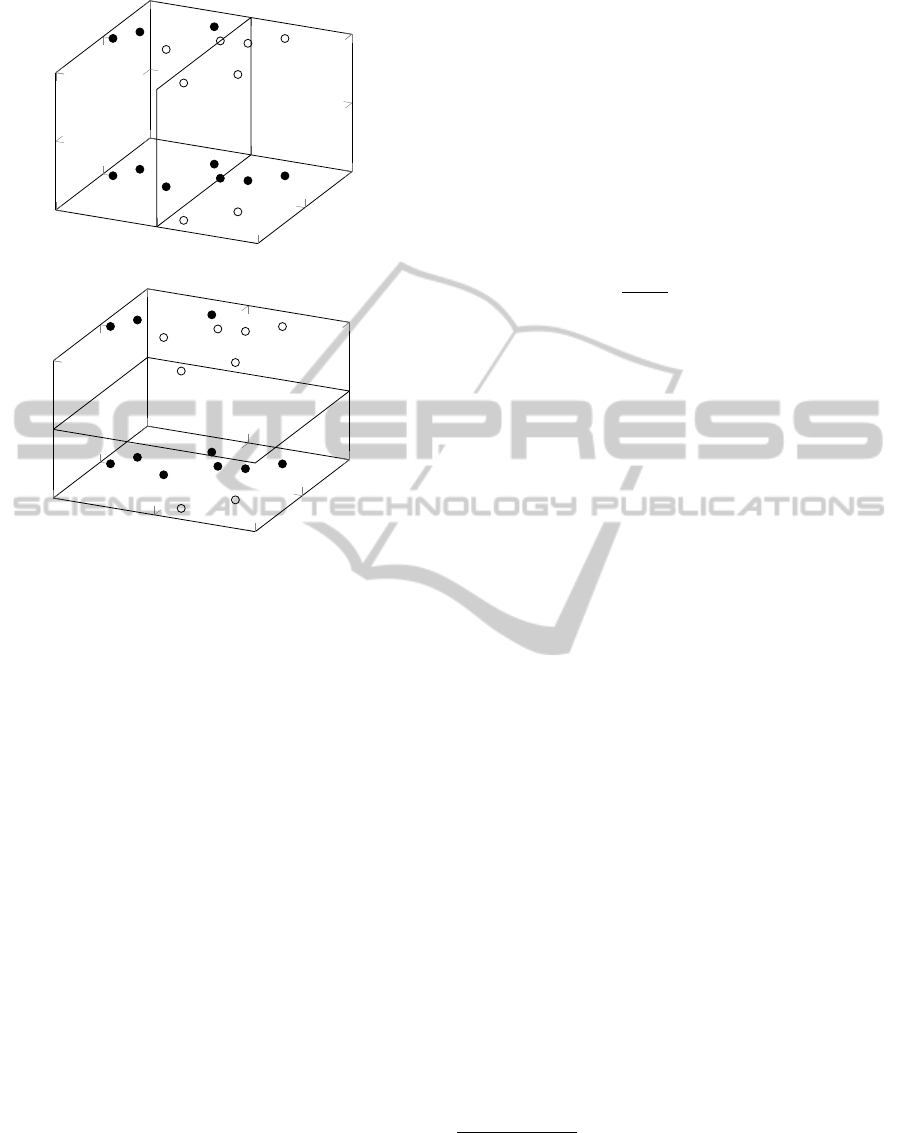
is not trivial, as illustrated in Figure 3 for an AD-
ABOOST with a decision stump. This is due to the
fact that a decision stump can only make cuts at one
attribute at a time, and therefore, as it can be imag-
ined, there are only two possible types of cuts in our
data replicated space:
• If the cut happens on one of the original attributes,
then the cuts on each replica will be on the same
position (see Figure 3(a)).
• If the cut happens on one of the new attributes,
then the cut will represent a constant factor on the
original space (see Figure 3(b)).
Note that the difficulties of instantiating the DRM
with ADABOOST remain true for any weak learner
that use a single attribute. Since in each iteration
a weak learner is designed without strong ties with
the other weak learners, the strong classifier resulting
from the boosting process may not possess the desired
property of consistency.
In here we propose a soft DRM, where the non in-
tersecting constraint is imposed on each iteration. Al-
though the final strong classifier may not possess that
property, intuitively, the final model is biased towards
consistent models.
In order to exploit the parallelism constraint that
is usually imposed by the Data Replication Method,
instead of training one weak classifier, we can train
(K − 1) weak classifiers (one for each replica), where
we force them to use the same attribute but with dif-
ferent thresholds. This will in turn guarantee that our
cuts are parallel. This makes our soft DRM a hybrid
of the original DRM and the Frank and Hall method.
We apply this idea to ADABOOST by indepen-
dently boosting each replica while forcing that, at
oAdaBoost-AnAdaBoostVariantforOrdinalClassification
71
0
2
4
0
2
4
0
0.5
1
(a)
0
2
4
0
2
4
0
0.5
1
(b)
Figure 3: Problems with decision stumps and the data repli-
cation model. (a) Cut on one of the new attributes. (b) Cut
on one of the original attributes.
every iteration, all weak classifiers use the same at-
tribute:
1. As before, we create (K −1) binary replicas of our
dataset;
2. Initialize the weights such as the sum of the
weights of each replica is 1;
3. Coupled selection of the weak classifier between
all replicas;
(a) For a decision stump, pick the best attribute
(possibly with different decision thresholds)
ˆ
att
based on a combination of the errors of each
replica;
4. Calculate the weight of each observation j in each
replica k at iteration i;
5. If a replica has an error superior to 50%, stop
boosting that replica;
6. The training stops if every replica has an error su-
perior to 50% or after a set number of iterations.
Note that the (K −1) binary ADABOOST are tied only
in step 3, which can be considered as part of build-
ing the weak learner.Also note the error of each weak
classifier is computed independently for each replica,
resulting also in an independent update of the weights
and in independent estimation of the contribution of
the binary weak classifier to the final binary strong
classifier. Moreover, the boosting process can stop
earlier in one replica than in the others. Nothing of
this is true for ADABOOST.OR.
When using the decision stump as weak classifier,
all (K − 1) replicas of ADABOOST are constrained
to use the same attribute but with (likely) different
thresholds. The attribute is chosen to minimize a
function (in our case we selected the average but the
median or the maximum were also sensible options)
of the individual (K − 1) errors:
argmin
att
1
K − 1
K−1
∑
k=1
Err
k
(att)
The individual error Err
k
(att) is the smallest mis-
classification error (by optimizing the threshold) in
replica k when using attribute att.
A more detailed explanation of this algorithm can
be seen on Algorithm 1.
4 EXPERIMENTAL STUDY
In order to compare the performance of the various
ADABOOST variants, we performed experiments on
both artificial and real-world datasets. All variants
were implemented on top of Weka’s ADABOOST.M1
implementation. The results were obtained by per-
forming 10 experiments using 10-fold cross valida-
tion, with the number of iterations limited to 100. The
statistical significance analysis was done in Weka’s
experimenter interface using a corrected paired t-test,
with a confidence of 0.05. The error metrics used
were the Mean Error Rate (MER) and the Mean Ab-
solute Error (MAE)
2
.
4.1 Ordinal Datasets
In our experiments we use two synthetic datasets and
six real datasets. A more detailed description of each
dataset is presented in Table 1.
The synthetic datasets are the following:
1. 1000 points x = (x
1
, x
2
)
t
were randomly gen-
erated in the unit square [0, 1] × [0, 1] ∈ R
according to the uniform distribution. The
class was assigned to each point accord-
ing to its distance to (0.5, 0.5): f (x) =
6 × ((x
1
− 0.5)
2
+ (x
2
− 0.5)
2
)
2
We calculated the absolute error in the following way:
If our predicted class is C
p
and the correct class is C
c
, then
the absolute error is |c − p|. Weka comes with an imple-
mentation of MAE for classification that is different from
the one we presented and is not suited for ordinal tasks, and
therefore should not be used to reproduce our results.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
72

Data: A dataset D = (D, f ) with N elements
Result: A classifier
ˆ
f
F
Replicate the dataset in K − 1 binary replicas D
k
= (D
k
, f
k
)
Initialize the example weights as w
j
k
:=
1
N
;
Initialize active
k
= true; i := 1;
while ¬EndingCondition do
forall the att ∈ Attributes do
forall the k : 0 ≤ k < K − 1 ∧ active
k
do
ˆ
f
i
k,att
= train(D
k
, att);
error
i
k,att
=
∑
N
j=1
w
j
k
[[
ˆ
f
i
k,att
(d
j
k
) 6= f (d
j
k
)]];
end
end
ˆ
att
i
= argmin
att
combination(error
i
k,att
) ; // The attribute to split on
forall the k : 0 ≤ k < K − 1 ∧ active
k
do
ˆ
f
i
k
=
ˆ
f
i
k,
ˆ
att
i
;
error
i
k
= error
i
k,
ˆ
att
i
;
if error
i
k
> 0.5 then
active
k
:= f alse; // Stop boosting this replica
else
α
i
k
= 0.5log(
error
i
k
1−error
i
k
) ; // Classifier weight
forall the j do
w
j
k
:= w
j
k
(α
i
k
)
1−[[
ˆ
f
i
k
(d
j
)6= f
k
(d
j
)]]
; // Updates the example weights
end
F
k
:= F
k
∪
ˆ
f
i
k
; // Binary ensemble for replica k
end
end
Normalize the weights so that ∀k :
∑
j
w
j
k
= 1;
i := i + 1
end
forall the k do
ˆ
f
F
k
(x) = sign(
∑
i
α
i
k
ˆ
f
i
k
(x)) ; // Binary classifier for replica k
end
ˆ
f
F
= getOrdinalClassifier(
ˆ
f
F
1
, ...,
ˆ
f
F
K−1
) ; // Combines the binary results.
Algorithm 1: oADABOOST with decision stump.
2. 1000 points from a dataset commonly used for
evaluating ordinal data methods (Cardoso and
da Costa, 2007) (this dataset is also shown on Fig-
ure 4).
In the Balance-Scale dataset each example rep-
resenting a balanced scale tipped to the right, to
the left or balanced, based on the relation between
the left distance, right distance, left weight and
right weight. It is available on the UCI reposi-
tory (https://archive.ics.uci.edu/ml/). The Arie Ben
David datasets are available on the MLData Repos-
itory (https://mldata.org/) and consist of examples
classified on a ordinal scale according to subjective
judgements (e.g. the degree of fitness of a candidate
to a certain job). The BCCT dataset, encompassing
1144 observations, expresses the aesthetic evaluation
0 0.2 0.4
0.6
0.8 1
0
0.2
0.4
0.6
0.8
1
1
1
2
2
3
4
4
5
5
Figure 4: Synthetic dataset.
oAdaBoost-AnAdaBoostVariantforOrdinalClassification
73

Table 1: List of considered datasets. The number of attributes excludes the class attribute and the SWD dataset has an unused
label.
Name Points Attributes Labels Class Distribution
Synthetic 1 (Circle) 1000 2 3 [523, 413, 63]
Synthetic 2 (Non-monotonic) 5000 2 5 [115, 296, 225, 229, 135]
Arie Ben David ERA 1000 3 9 [92, 142, 181, 172, 158, 118, 88, 31, 18]
Arie Ben David ESL 488 4 9 [2, 12, 38, 100, 116, 135, 62, 19, 4]
Arie Ben David LEV 1000 4 5 [93, 280, 403, 197, 27]
Arie Ben David SWD 1000 10 4(5) [32, 352, 399, 217]
Balance-Scale 625 4 3 [288, 49, 288]
BCCT 1144 30 4 [160, 592, 272, 120]
of Breast Cancer Conservative Treatment (Cardoso
and Cardoso, 2007; Cardoso and Sousa, 2011). For
each patient submitted to BCCT, 30 measurements
were recorded, capturing visible skin alterations or
changes in breast volume or shape. The aesthetic
outcome of the treatment for each and every patient
was classified in one of the four categories: Excellent,
Good, Fair and Poor.
4.2 Results
In Table 2 we show a comparison of the follow-
ing ADABOOST variants, instantiated with Decision
Stumps, limited to 100 iterations:
oADABOOST Our ADABOOST variant.
ADABOOST.M1 One of the most common AD-
ABOOST variants with support for multiple
classes (Freund et al., 1996).
ADABOOST.M1W A small variant of the AD-
ABOOST.M1 algorithm designed to have better
performance on problems with many possible
classes (Eibl and Pfeiffer, 2002).
ADABOOST.OR A variant of the ADABOOST.M1
designed for ordinal classification (Lin and Li,
2009). Since it needs an ordinal classifier as the
weak learner, we use a decision stump that picks
(K − 1) cuts on the same attribute.
Frank and Hall (with ADABOOST) The method
proposed by Frank and Hall (Frank and Hall,
2001) instantiated with ADABOOST. Note that
in this method the (K − 1) weak learners are
independently designed, while in our proposed
oADABOOST method they are coupled.
Results seem to also indicate a slight superi-
ority of ADABOOST.M1W over ADABOOST.M1,
more clear in the datasets with more classes. AD-
ABOOST.OR seems superior to ADABOOST.M1W
and ADABOOST.M1, suggesting that the integra-
tion of the knowledge of the order in the design
brings performance advantages. It is also possible
to see that oADABOOST and Frank and Hall meth-
ods present the most favorable results when com-
pared to the other boosting algorithms under compari-
son. The performance difference between our method
oADABOOST and Frank and Hall instantiated with
ADABOOST seems negligible. However, note that
since oADABOOST is constrained to use the same at-
tribute in all (K − 1) weak learners (which is not the
case in the Frank and Hall method), it results in sim-
pler models without loss of performance.
(a) (b)
(c)
Figure 5: Boundaries generated by (a) oADABOOST, (b)
Frank and Hall (with ADABOOST) and (c) ADABOOST.OR
on our synthetic non-monotonic dataset.
Based on the boundaries of the various classi-
fiers trained on our synthetic non-monotonic dataset
(Figure 5), it appears that ADABOOST.OR has more
problems with noise, while both oADABOOST and
the Frank and Hall method have problems with non-
monotonicity.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
74

Table 2: Comparison of oADABOOST with ADABOOST variants.
(a) Mean Error Rate: mean (standard deviation) of 10 experiments
Dataset oADABOOST ADABOOST.M1 ADABOOST.M1W ADABOOST.OR Frank and Hall
Circle 0.07(0.03) 0.40(0.03)• 0.55(0.01)• 0.16(0.04)• 0.07(0.03)
Non-mon. 0.66(0.03) 0.70(0.02)• 0.61(0.05)◦ 0.76(0.02)• 0.50(0.04)◦
ERA 0.75(0.04) 0.78(0.02) 0.78(0.04) 0.78(0.02) 0.73(0.05)
ESL 0.33(0.06) 0.57(0.03)• 0.47(0.06)• 0.45(0.05)• 0.33(0.06)
LEV 0.38(0.04) 0.58(0.03)• 0.42(0.05)• 0.50(0.04)• 0.38(0.05)
SWD 0.43(0.05) 0.48(0.04)• 0.48(0.05)• 0.48(0.04)• 0.43(0.05)
Balance 0.03(0.02) 0.28(0.04)• 0.08(0.02)• 0.17(0.08)• 0.04(0.02)
BCCT 0.13(0.03) 0.37(0.03)• 0.38(0.05)• 0.32(0.03)• 0.13(0.03)
(b) Mean Absolute Error: mean (standard deviation) of 10 experiments
Dataset oADABOOST ADABOOST.M1 ADABOOST.M1W ADABOOST.OR Frank and Hall
Circle 0.07(0.03) 0.44(0.03)• 0.55(0.01)• 0.16(0.04)• 0.07(0.03)
Non-Mon. 0.99(0.07) 1.30(0.08)• 1.19(0.14)• 1.03(0.04) 1.02(0.03)
ERA 1.24(0.10) 1.43(0.07)• 1.44(0.12)• 1.43(0.07)• 1.34(0.13)•
ESL 0.35(0.07) 0.73(0.06)• 0.56(0.08)• 0.51(0.07)• 0.35(0.07)
LEV 0.41(0.05) 0.71(0.03)• 0.46(0.06)• 0.57(0.05)• 0.42(0.06)
SWD 0.45(0.05) 0.50(0.04)• 0.54(0.06)• 0.50(0.04)• 0.46(0.05)
Balance 0.03(0.02) 0.49(0.09)• 0.08(0.02)• 0.18(0.09)• 0.04(0.02)
BCCT 0.13(0.03) 0.38(0.03)• 0.40(0.07)• 0.33(0.03)• 0.14(0.03)
◦, • statistically significant improvement or degradation.
5 CONCLUSIONS
In this work we have presented a new variant of the
well known ADABOOST algorithm designed for or-
dinal classification. In the proposed methodology,
(K − 1) binary ADABOOST are built in parallel, tied
in phase of designing the weak learner. In the end,
the (K − 1) strong binary classifiers are combined to
yield the multiclass model.
Based on our results, it appears that by enforc-
ing local constraints at each boosting iteration (in this
case, by enforcing local parallelism) and by working
on the replicated space, one can achieve better re-
sults on ordinal classification tasks, when compared
to other ADABOOST variants instantiated with deci-
sion stumps. We plan now to extend these ideas to
other learning methodologies whose behaviour is sim-
ilar to ADABOOST (i.e. the final classifier is built
from a set of weak classifiers that only use one at-
tribute), such as decision trees (which should have
less issues with non-monotonic datasets, since the
recursive division of the space should lead to small
monotonic cells). We also plan to study the impact
of stronger restrictions on the set of weak classifiers
(e.g. enforce the splits to be ordered), as that should
lead to classifiers more similar to the ones generated
via the original DRM.
ACKNOWLEDGEMENTS
This work is financed by the ERDF - European Re-
gional Development Fund through the COMPETE
Programme (operational programme for competitive-
ness) and by National Funds through the FCT within
project PTDC/SAU-ENB/114951/2009. The work
leading to these results has received funding from
the European Community’s Seventh Framework Pro-
gramme under grant agreement n FP7–600948. The
authors would also like to thank the Masters in Infor-
matics and Computing Engineering and Department
of Informatics Engineering of the Faculty of Engi-
neering of the University of Porto for supporting some
of the costs of this work.
REFERENCES
Cardoso, J. S. and Cardoso, M. J. (2007). Towards an intel-
ligent medical system for the aesthetic evaluation of
breast cancer conservative treatment. Artificial Intel-
ligence in Medicine, 40:115–126.
Cardoso, J. S. and da Costa, J. F. P. (2007). Learning to clas-
sify ordinal data: the data replication method. Journal
of Machine Learning Research, 8:1393–1429.
Cardoso, J. S. and Sousa, R. (2010). Classification models
with global constraints for ordinal data. In Proceed-
ings of The Ninth International Conference on Ma-
chine Learning and Applications (ICMLA), pages 71–
77.
oAdaBoost-AnAdaBoostVariantforOrdinalClassification
75

Cardoso, J. S. and Sousa, R. (2011). Measuring the per-
formance of ordinal classification. International Jour-
nal of Pattern Recognition and Artificial Intelligence,
25(8):1173–1195.
Cardoso, J. S., Sousa, R., and Domingues, I. (2012). Ordi-
nal data classification using kernel discriminant anal-
ysis: A comparison of three approaches. In Pro-
ceedings of The Eleventh International Conference on
Machine Learning and Applications (ICMLA), pages
473–477.
Eibl, G. and Pfeiffer, K. P. (2002). How to make adaboost.
m1 work for weak base classifiers by changing only
one line of the code. In Machine Learning: ECML
2002, pages 72–83. Springer.
Frank, E. and Hall, M. (2001). A simple approach to ordinal
classification. Springer.
Freund, Y., Iyer, R., Schapire, R. E., and Singer, Y. (2003).
An efficient boosting algorithm for combining prefer-
ences. Journal of Machine Learning Research, 4:933–
969.
Freund, Y. and Schapire, R. E. (1995). A decision-theoretic
generalization of on-line learning and an application
to boosting. In Proceedings of the Second European
Conference on Computational Learning Theory, Eu-
roCOLT ’95, pages 23–37. Springer-Verlag.
Freund, Y., Schapire, R. E., et al. (1996). Experiments with
a new boosting algorithm. In ICML, volume 96, pages
148–156.
Lin, H.-T. and Li, L. (2006). Large-margin thresholded en-
sembles for ordinal regression: Theory and practice.
In Balc
´
azar, J., Long, P., and Stephan, F., editors, Al-
gorithmic Learning Theory, volume 4264 of Lecture
Notes in Computer Science, pages 319–333.
Lin, H.-T. and Li, L. (2009). Combining ordinal pref-
erences by boosting. In Proceedings ECML/PKDD
2009 Workshop on Preference Learning, pages 69–83.
Sousa, R. and Cardoso, J. S. (2011). Ensemble of deci-
sion trees with global constraints for ordinal classifi-
cation. In International Conference on Intelligent Sys-
tems Design and Applications (ISDA).
Sun, B.-Y., Wang, H.-L., Li, W.-B., Wang, H.-J., Li, J.,
and Du, Z.-Q. (2014). Constructing and combining
orthogonal projection vectors for ordinal regression.
Neural Processing Letters, pages 1–17.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
76
