Parallel Shortest-path Searches in Multiagent-based Simulations with

PlaSMA

Max Gath, Otthein Herzog and Maximilian Vaske

Institute Institute for Artificial Intelligence, TZI - Center for Computing and Communication Technologies,

Bremen, Germany

Keywords: Multiagent-based Simulation, Shortest-path Algorithms, PlaSMA, JADE, Planning and Scheduling,

Autonomous Logistic Processes.

Abstract: The goods structure effect increases the complexity and dynamics of logistic processes. To handle the

resulting challenges and requirements, planning and controlling of logistic processes have to be reliable and

adaptive. Especially in these dynamic environments, Multiagent-Based Simulation (MABS) is a suitable

approach to support decision makers in order to evaluate the companies' processes and to identify optimal

decisions. This paper presents the PlaSMA multiagent simulation platform, which has been developed for

the evaluation of logistics scenarios and strategic analyses. As shortest-path searches are an essential but

cost intensive part of the agents for the simulation of transport processes, we focus on the parallel

application of a state-of-the-art Hub Labeling algorithm, which is combined with Contraction Hierarchies.

The results show, that the optimal number of concurrently running routing agents is restricted by available

cores and/or the number of agents running physically concurrently. Moreover, by slightly restricting the

agents' autonomy a significant increase in runtime performance can be achieved without losing the

advantages of agent-based simulations. This allows to simulate large real-world transport scenarios with

MABS and low hardware requirements.

1 INTRODUCTION

The so-called goods structure effect refers to a

change of the economic and logistic structure: The

production of bulk goods which are transported in

large quantities by bulk cargo transport has been

decreased, while the amount of individualized high-

end products has been increased. This trend is

aggravated by the so-called Industry 4.0 – the Fourth

Industrial Revolution and the consequent integration

of the Internet of Things and Services in production

and logistics processes based on Cyber Physical

Production Systems.

As a result, there is a much higher amount of

small-sized shipments, which have to be delivered

within guaranteed time windows and probably

within a few hours. The demanding customer

requirements and the growing cost pressure in the

logistic sector thus forces logistic transport service

providers to optimize the efficiency of their

processes.

Multiagent systems can be used to solve

complex, dynamic, and distributed problems

(Müller, 1997) in which agents are a natural

metaphor for physical objects and actors (Jennings

and Wooldridge, 1998, p. 7). Consequently,

multiagent systems are an adequate technology for

the modeling and the optimization of logistic

processes. It has been shown that their application to

logistics increases the efficiency as well as the

service quality and contributes to reduce the costs

significantly (cf. Gath et al., 2013; Dorer et al.,

2005; Fischer, 1995; Schuldt, 2011). Multiagent-

Based Simulation (MABS) combines concepts of

multiagent systems and simulation. Applying MABS

allows for the analysis of MAS before their

deployment to real world processes. Thus, it is

possible to investigate the impact of potential

changes, to calculate expected benefits, and to

identify risks that may arise by switching to new

processes and the integration of new technologies

such as MAS in advance. This is especially relevant

in scenarios where the quality of the results depends

on the outcome and/or sequence of agent

negotiations that cannot be predicted in advance

(Jennings, 2001). Moreover, MABS allows for

Gath M., Herzog O. and Vaske M..

Parallel Shortest-path Searches in Multiagent-based Simulations with PlaSMA.

DOI: 10.5220/0005195100150021

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence (ICAART-2015), pages 15-21

ISBN: 978-989-758-073-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

precise scenario investigations and strategic

analyses. For instance, effects of new pricing models

or the impact of economic cycles and natural

disasters on the supply chain can be determined.

The goal of this research is to optimize the

runtime performance of MABS in logistics. Section

2 presents the MABS framework PlaSMA, which

has been developed for simulations of logistic

processes. As shortest-path searches are cost-

intensive operations in this domain, Section 3

provides an implementation of a state-of-the-art

shortest-path algorithm which applies Hub-Labeling

in combination with Contraction Hierarchies. The

advantage of applying a Hub-Labeling algorithm in

MABS is, that shortest-path queries are calculated

by fast processed read-only operations on the

underlying graph (in contrast to classical algorithms

such as Dijkstra's algorithm (Dijkstra, 1959)). Thus,

several agents may perform searches on the same

algorithm concurrently. Section 4 investigates

established modeling approaches and identifies a

memory efficient solution, which exploits the

properties of the algorithm to optimize the runtime

performance significantly. The result facilitates the

simulation of real-world multiagent scenarios in

transport logistics with less hardware requirements

compared to other established modeling approaches.

2 THE PlaSMA SIMULATION

PLATFORM

The PlaSMA simulation platform (Warden et al.,

2010) is an agent-based event driven simulation

platform that has been designed for modeling,

simulation, evaluation, and optimization of planning

and control processes in logistics. It extends the

FIPA-compliant Java Agent DEvelopment

Framework (JADE) (Bellifemine et al., 2007) for

agent communication and coordination. PlaSMA

provides discrete time simulations, which allow for

precise simulations of processes with small

simulated time intervals (with intervals of at least

1ms). Furthermore, it ensures correct

synchronization and reproducibility (Gehrke et al.,

2008). For instance, the simulation framework

guarantees, that message transfer consumes

simulated time, because transferring messages

consumes physical time in real-world processes as

well. Consequently, the consistency of each agent

(e.g., no agent receives messages from the future and

all the agents' knowledge is consistent at a certain

point of simulated time) is also guaranteed by a

conservative synchronization mechanisms (cf.

Gehrke et al., 2008 for more details). The time

model adequacy is assured by a parameter which

controls the maximum and minimum simulated time

interval for the synchronization. Thus, PlaSMA is

capable to simulate scenarios that require fine-

grained and coarse time discretization as well.

Moreover, it supports the integration of real-

world infrastructures by the import of geographic

information from OpenStreetMap and of timetable

information (e.g., for bus lines or tram lines), which

matches the standards of the Association of German

Transport Companies (VDV) (Greulich et al. 2013).

The transport infrastructure is represented by a

directed graph where edges represent ways, such as

waterways, rails, and roads while nodes represent

traffic junctions that connect edges with each other.

The type of the road (e.g., highway, inner city road,

or pedestrian way) including its properties (e.g.,

speed limits, exact distances, and one-way

restrictions) is further specialized automatically by

processing the respective information provided by

the OpenStreetMap (see: http://openstreetmap.org)

dataset. Thus, PlaSMA allows for modeling fine-

grained infrastructures with road sections whose

speed limits are changing. As shortest-path searches

(see Section 3) on models of real-world

infrastructures are some of the most cost intensive

operations in logistic transport scenarios, this paper

focuses on an efficient implementation and

modeling of multiagent systems for scenarios that

require shortest-path information.

Figure 1: The graphical user interface of the PlaSMA

simulation platform.

In order to reliably simulate industrial and

transport processes, PlaSMA is capable of

incorporating process data of cooperating companies

and partners, e.g., customer orders or service

requests, directly into the simulation platform. This

allows for a precise analysis of real logistic

processes with low costs. Batch-runs, process

visualization, as well as automated measurements of

individually defined performance indicators allow

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

for fast and significant process evaluations. Figure 1

shows the graphical user interface of PlaSMA. The

software can be downloaded at

http://plasma.informatik.uni-bremen.de.

3 HUB-LABELING WITH

CONTRACTION

HIERARCHIES

Efficient shortest-path searches are essential for the

simulation of logistic transport processes, e.g., to

compute distance matrices for solving the Vehicle

Routing Problem (Golden et al., 2008; Gath et al.,

2013) or the Pickup and Delivery Problem (Parragh

et al., 2008). However, they are cost intensive

operations especially on real-world graphs. XXX

have shown that particularly in MABS Hub-

Labeling (HL) (Abraham et al., 2011) in

combination with Contraction Hierarchies (CH)

(Geisberger et al., 2012) outperforms classical

algorithms such as the Dijkstra (Dijkstra, 1959) or

the well-known A-Star algorithm. For the sake of

completeness, we present the general idea of our

implemented Hub-Labeling algorithm similarly to

Gath et al., (2014).

The idea of distance labeling algorithms is that

the distance between two nodes is only determined

by the comparison of their assigned labels, which are

ideally computed offline. Therefore, search queries

on the pre-computed labels can be performed online

efficiently. In our implementation, the Hub Labels

contain a list with references to multiple other nodes

(the hubs). Within the construction process of the

labels, the so-called cover property has to be

fulfilled. Thus, both labels of any two vertices

and must contain the same vertex that is on the

shortest - path (Abraham et al., 2012, pp. 25-26).

Thus, it is guaranteed that all shortest paths in a

graph can be determined by the labels of the source

and target nodes. The challenge is to create memory-

efficient labels that fulfill the cover property.

Applying the labeling algorithm on nodes which

are saved in Contraction Hierarchies (CH), allows

for memory-efficient label representations. In order

to build the CH, the original graph  is extended to a

larger graph ' which contains direct shortcuts

between nodes instead of shortest paths in. The

algorithm iterates over all nodes and saves each

node in the next higher level of the hierarchy. In this

process, it calculates possible shortest path shortcuts

to other nodes. Therefore, the current node is

considered to be removed from the graph and it is

checked if all other shortest paths would still be

included within the graph without this node. If a

shortest path originally passed the "removed" node,

a new shortcut is created to retain this shortest path.

In general, the performance of the algorithm

depends on the sequence of nodes in which they are

added to the CH (Geisberger et al., 2012). To

determine the next node that will be processed, all

unprocessed nodes are sorted by a priority value.

The node with the highest priority is processed next.

The priority value of a node is mainly computed by

the edge difference between the current graph and

the graph with the shortcuts that result from

processing that node. Some priorities have to be

updated continuously after adding a new node to the

CH, because in every iteration the graph might be

extended by a new shortest path. Due to the fact that

the computation of the priorities is a cost-intensive

operation, the value is estimated. The better the

sequence of the iterated/selected nodes is, the less

shortcuts are determined, and the more efficient is

the memory consumption and the search on the CH.

In addition, there are also approaches which can be

applied to time-dependent graphs (Batz et al., 2008)

or to dynamically changing graphs (Geisberger et

al., 2012).

Next, the Hub-Labels are computed. This process

starts at the highest level of the CH. For each level

(node) a label is created. The label contains all

references and information about the shortest

distance to nodes of higher levels. Further

optimization techniques to reduce the memory are

not implemented yet, but provided by Abraham et al.

(2012) (pp. 26).

4 PARALLEL SHORTEST-PATH

SEARCHES IN AGENT-BASED

SIMULATION

In numerous multiagent-based approaches in

logistics, the decision making of agents requires

shortest-path information (cf. Gath et al., 2013;

Dorer et al., 2005; Fischer et al., 1995). In general,

there are only two options to acquire this

information. On the one hand the agent can compute

the shortest paths by itself. On the other hand the

agent might ask a service provider agent (a so-called

routing agent) which receives a routing request,

computes the shortest path, and finally sends the

result back to the respective agent. The goal is to

determine an adequate way of modeling for a

scenario in which numerous routing requests have to

ParallelShortest-pathSearchesinMultiagent-basedSimulationswithPlaSMA

be answered immediately (e.g., to compute distance

matrices of cities). Especially if we apply the Hub-

Labeling algorithm in combination with Contraction

Hierarchies, it is not sufficient to consider the

performance to handle search queries online, but

also necessary to include the time for the creation of

the Hub-Labels and CH as well as the memory

consumption, which is required to save all the labels.

In the following, we will investigate several

scenarios.

In the first case, each agent has its full autonomy

and relies not on other agents. However, each agent

has to build and save its own Hub-Labels. This is

time- and memory-intensive. In the second case, the

memory and time consuming shortest-path

operations are sourced out to one or several routing

agents. Each routing-agent must build and save the

Hub-Labels. The optimal number of parallel running

routing agents has to be determined.

Beside the above mentioned options, there is

another modeling approach that slightly violates the

agent's autonomy. It is possible to build the Hub-

Labels by a single agent and save it in a static

variable. While classical routing algorithms such as

the Dijkstra algorithm manipulate the graph by

saving distance information at the nodes to compute

the shortest paths, the HL algorithm performs

instead read-only operations on the graph. Thus,

each agent can directly access this static variable and

perform the routing requests by their own in parallel.

Depending on the computer architecture the

multiagent system is running on, these operations

are performed also physically concurrently.

However, this slightly violates the agent's autonomy,

because all agents (running on the same JVM) share

the same component. Thus they are not fully

independent of each other. Note, that PlaSMA

extends JADE, thus, each static variable is only

visible on the Java Virtual Machine (JVM).

Nevertheless, distributed simulations on multiple

machines are supported by PlaSMA. In this case,

each machine requires its own static routing

algorithm.

4.1 Experimental Setup

In this chapter, we will investigate a scenario with

1,000,000 routing requests of several agents, which

have to be answered immediately (e.g., to compute

distance matrices of cities). The goal is to determine

an adequate model which optimizes the run-time

performance of the simulation with a reasonable

memory consumption.

In order to satisfy real word requirements, we

modeled the whole transport infrastructure of

Liechtenstein with 3,607 nodes and 8,401 edges. For

the evaluation in reasonable time on conventional

hardware, we chose this area with a restricted

number of nodes and edges, because this allows to

pinpoint significant results by measuring average

values of 10 runs in each setting. Nevertheless, the

algorithm has successfully been applied to larger

infrastructures with more than 300,000 edges and

200,000 nodes. The 1,000,000 search queries are

requested by 50 agents. Thus, each agent asks for

20,000 shortest paths. The simulation is started with

an agent, which generates 20,000 search queries

with randomized start and end nodes for each of the

50 consumer agents which are created. In order to

guarantee the reproducibility of runs, the random

seed in each experiment is fixed.

In Scenario 1, each consumer agent applies its

own shortest-path algorithm. Thus, the agents start a

preprocessing step to build up the Hub-Labels as

well as the Contraction Hierarchy and process all

their queries by themselves.

In Scenario 2, the shortest-path algorithm is

implemented by the Singleton Pattern (Gamma et

al., 1995, pp. 127). As a result, there exists only a

single instance of the algorithm on each JVM. All

consumer agents process their queries by

themselves, but operate on the same algorithm saved

in a static variable.

In Scenario 3 - 12, a varying number of routing

agents are created. They maintain their own shortest-

path algorithm and receive all the queries from the

consumer agents by a FIPA-compliant ACL-

Message. Next, the routing agents compute the

shortest path of the assigned requests and send an

ACL Message with the answer back to the agent.

The assignment of search requests to routing agents

is uniformly distributed. The reproducibility of this

assignment is also ensured by applying a fixed

random seed.

All the simulations run on a notebook computer

with an Intel quad-core i5-2500k processor,

Windows 7 64bit, and 16 GB RAM.

4.2 Results

In each scenario four performance indicators were

measured. The most significant is the total (physical)

simulation time. Moreover, two performance

indicators determine the time required for

preprocessing. This is the earliest time an agent ends

its preprocessing step and the elapsed time for all the

agents to finish building the Hub-Labels and

Contraction Hierarchies. The measured performance

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

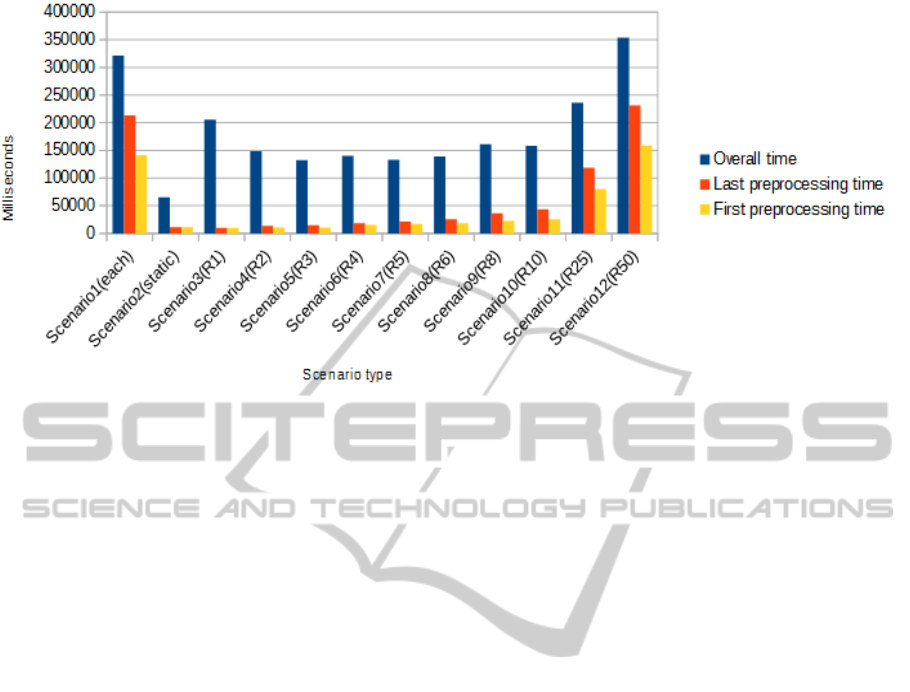
Figure 2: The average simulation time and the time required to create the Hub-Labels (of 10 runs).

indicators are average values of 10 runs. The results

are shown in Figure 2.

As the shortest-path algorithm only performs

read-only operations, the memory requirements of

the whole agent system, increases proportional to the

number of graph instances, which are created and

saved concurrently by all the agents. This is obvious,

but also rechecked in these investigations.

4.3 Discussion

The results show that providing the full autonomy of

agents requires a higher memory utilization and

longer runtime. Each agent must create and maintain

its own routing algorithm. On a quad-core

architecture, this process cannot be parallelized

physically on 50 agents, but has to be performed

sequentially. Thus, sourcing out the cost-intensive

operations to routing agents is reasonable. As a

result, the preprocessing time as well as the total

simulation time is reduced. In JADE each agent has

its own process. However, if there is just a single

routing agent, the hardware utilization is only about

25% on a quad-core processor, because all the

search queries are executed by a single agent on a

single core. Thus, the preprocessing time and the

total simulation time can be reduced by physically

concurrently running routing agents as long as the

number of routing agents is lower or equal to the

number of available cores. Consequently, the search

queries are answered in parallel and the hardware

utilization is increased. If the number of routing

agent exceeds the amount of cores, the

preprocessing for the creation of the Hub-Labels

cannot be performed in parallel anymore and the

total time for preprocessing and simulation is

increased. If each consumer agent has its own

routing agent, the performance is even higher

compared to the case that each agent has its own

algorithm. This is explained by the fact, that the

message transfer within the multiagent system

consumes additional time.

Moreover, the results show that the shortest

running time (and also the lowest memory

utilization) is reached by the static implementation

of the routing algorithm. Note that this is only

possible if the shortest-path algorithm performs

read-only operations during the search such as Hub-

Labeling on CH. Even if we compare the result of

this modeling approach to the outcome of the

scenario with four routing agents (where all the

preprocessing steps are performed concurrently), the

running time is significantly lower. This has two

reasons: On the one hand, no communication

between agents is required. On the other hand, the

capacity utilization of the hardware is higher,

because the algorithm answers four requests in

parallel at any time. When a computation is finished,

the next shortest path is computed immediately

afterwards. In contrast, with four routing agents each

agent computes its assigned shortest-path requests

and when they are finished they have to wait until

the last agent has finished its computation as well.

5 CONCLUSION AND OUTLOOK

MABS is a promising approach to evaluate and

optimize logistic processes. Although it is possible

to increase the scalability of MABS platforms in

ParallelShortest-pathSearchesinMultiagent-basedSimulationswithPlaSMA

general (Ahlbrecht et al., 2014) or adding some

optimization support for executing them on parallel

processors (e.g. Sano et al., 2014), shortest-path

searches remain one of the most cost-intensive

operations of the agents in logistic scenarios.

Therefore, we investigated and compared several

modeling options for shortest-path searches in the

PlaSMA simulation platform.

The implemented shortest-path algorithm is a

state-of-the-art algorithm, which applies Hub-

Labeling with Contraction Hierarchies. As Hub-

Labeling algorithms apply read-only operations for

answering search requests, several agents can share

the same (static) algorithm and perform their queries

concurrently. The results reveal that slightly

restricting the autonomy of agents by applying a

single algorithm saved in a static variable (which is

part of all the agents) leads clearly to the lowest

runtime of the simulation and lowest memory

consumption.

As long as all agents run on the same machine

(and same JVM), the disadvantage of less autonomy

in this modeling approach is of more theoretical

meaning than practically relevant. For instance, the

robustness could even be guaranteed by a second

redundant static instance of the algorithm. The

privacy is also guaranteed, because the agents must

not reveal their search queries to any other agent.

However, if the “full” autonomy of the agents

has to be guaranteed, another option is to create

several routing agents that receive routing requests,

perform shortest-path searches, and provide the

results. Although this approach consumes more time

for the whole simulation, i.e., because of the

increased time for message transfer and

synchronization of agents, it can still profit from

concurrent calculations as long as the number of

routing agents is equal or lower than the number of

available cores. Otherwise, the redundant algorithms

consume a high amount of memory (in particular if

the shortest-path searches are performed on large

graphs), and time for communication and

computation, because shortest paths are not

performed physically concurrently. In an extreme

case it is even preferable that each consumer agent

has its own algorithm. In this case the autonomy of

the agents is maximized and less communication is

required.

In conclusion, applying a static Hub-Labeling

algorithm in MABS, which is part of all agents,

allows for concurrent calculations, improves the

runtime performance of the simulation significantly,

and reduces the memory usage. In contrast to the

other established modeling approaches, this

facilitates the simulation of large real-world

scenarios with less hardware requirements.

Future research will focus on the application of

shortest-path algorithms on several distributed

machines. For instance, the PlaSMA simulation

platform supports the simulation of multiple agents

that run on containers located on different machines.

Moreover, we will investigate the behavior of

shortest-path algorithms for dynamically changing

graphs. In this case, the Hub-Labels have to be

updated after the preprocessing is finished.

ACKNOWLEDGEMENTS

The presented research was partially funded by the

German Research Foundation (DFG) under

reference number HE 989/14-1 (project Autonomous

Courier and Express Services) at the University

Bremen, Germany.

REFERENCES

Abraham, I., Delling, D., Goldberg, A.V., Werneck, R.F.,

2011. A hub-based labeling algorithm for shortest

paths in road networks. In: Experimental Algorithms.

10th Int. Sympo. SEA 2011, Lecture notes in Computer

Science, vol 6630. Springer, Berlin, pp 230-241.

Abraham, I., Delling, D., Goldberg, A.V., Werneck, R.F.,

2012. Hierarchical hub labelings for shortest paths. In:

Algorithms - ESA 2012. 20th Annual European

Symposium, Ljubljana, September 2012. Lecture notes

in computer science, vol 7501. Springer, Berlin, pp

24-35.

Ahlbrecht T., Dix, J., Köster, M., Kraus, P., Müller, J. P.,

2014. A scalable runtime platform for multiagent-

based simulation. In Proceedings of the 2nd

International Workshop on Engineering Multi-agent

Systems (EMAS2014)

Batz, G. V., Delling, D., Sanders, P., Vetter, C., 2008.

Time-dependent contraction hierarchies. In:

Proceedings of the 11

Works on Alg. Engineering

and Experiments, New York.

Bellifemine, F., Caire, G., Greenwood, D., 2007.

Developing multi-agent systems with jade. Chichester,

UK, Jon Wiley & Sons.

Dijkstra, E. W., 1959. A note on two problems in

connexion with graphs. Num. Math. 1:269-271.

Dorer, K., Calisti, M., 2005. An adaptive solution to

dynamic transport optimization. In: Proc. of the 4th

Int. Conf. on Autonomous Agents and Multiagent

Systems, ACM Press, pp. 45-51.

Fischer, K., Müller, J. P., Pischel, M., 1995. Cooperative

transportation scheduling: an application domain for

dai. Journal of Applied Artificial Intelligence 10:1-33.

Gamma, E., Johnson, E. R., Helm, R., Vlissides, J., 1995.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

Design patterns: elements of reusable object-oriented

software. Addison-Wesley.

Gath, M., Herzog, O., Edelkamp, S. , 2013. Agent-based

Planning and Control for Groupage Traffic, In: Proc.

of the 10th International Conf. & Expo on Emerging

Technologies for a Smarter World (CEWIT2013),

IEEE, Melville, USA.

Gath, M., Herzog, O., Vaske, M., 2014. The Impact of

Shortest Path Searches to Autonomous Transport

Processes, In: 4th International Conference on

Dynamics in Logistics (LDIC), Bremen, Germany (to

appear).

Geisberger, R., Sanders, P., Schultes, D., Vetter, C., 2012.

Exact routing in large road networks using contraction

hierarchies. Transportation Science 46:388-404.

Gehrke, J. D., Schuldt, A., Werner, S., 2008. Quality

criteria for multiagent-based simulations with

conservative synchronisation. In: Proc. of the 13th

ASIM Dedicated Conf. on Simulation in Production

and Logistics. Fraunhofer IRB Verlag, Stuttgart, pp.

545-554.

Golden, B., Raghavan, S., Wasil, E., (eds) 2008. The

vehicle routing problem: latest advances and new

challenges. Springer, New York.

Greulich, C., Edelkamp, S., Gath, M., 2013. Agent-based

multimodal transport planning in dynamic

environments. In: Advances in Artificial Intelligence -

36th Annual German Conference on Artificial

Intelligence, vol. 8077, Springer, Koblenz, Germany,

pp.74-85.

Jennings, N. R., 2001. An agent-based approach for

building complex software systems. Communication

of the AM 44(4):35-41

Jennings, N. R., Wooldridge, M., 1998. Applications of

intelligent agents. Springer-Verlag.

Müller, H. J., 1997. Towards Agent Systems Engineering.

Data & Knowledge Engineering, 23 (3): 217 - 245.

Parragh, S. N., Doerner, K. F., Hartl, R. F., 2008. A survey

on pickup and delivery problems part I: transportation

between customers and depot. Journal für

Betriebswirtschaft 58(1):21-51.

Sano, Y., Kadono, Y., & Fukuta, N., 2014. A Performance

Optimization Support Framework for GPU-based

Traffic Simulations with Negotiating Agents. In Proc.

of 7th Int. Workshop on Agent-based Complex

Automated Negotiations (ACAN2014).

Schuldt, A., 2011. Multiagent coordination enabling

autonomous logistics. Springer, Berlin.

Warden, T., Porzel, R., Gehrke, J. D., Herzog, O., Langer,

H., Malaka, R., 2010. Towards ontologybased

multiagent simulations: the plasma approach. In: Proc.

of the Euro. Conf. on Modelling and Simulations

(ECMS), pp 50-56.

ParallelShortest-pathSearchesinMultiagent-basedSimulationswithPlaSMA